考虑源荷碳责任分摊的新型电力系统多级灵活性资源规划

边晓燕，吴 珊，赵 健，许 凌，周 波，林顺富

（1.上海电力大学 电气工程学院，上海 200090；2.国家电网有限公司华东分部，上海 200120）

0 引言

新型电力系统规划是推动电力系统清洁低碳转型的技术前提。为满足能源环境的低碳化诉求，有必要在新型电力系统规划问题中充分融合碳理念及相关技术，开展低碳电力系统规划研究。同时，风、光等新能源的强不确定性加剧了净负荷波动，系统灵活性需求增大，而源-网-荷-储侧多元资源的灵活供给能力尚未得到充分发挥，有必要在探索电力系统低碳清洁转型路径的同时解决高比例新能源所带来的灵活性问题，研究统筹考虑新型电力系统低碳化和灵活性需求的规划方法。

目前针对新型电力系统规划问题已开展了一定研究，主要从“电视角”进行新型电力系统灵活性规划和从“碳视角”进行低碳电力系统规划［1］2 个角度进行考虑。从“电视角”出发的灵活性规划方面，主要研究强不确定性和波动性新能源带来的灵活性问题：文献［2］建立了考虑灵活性供需平衡的源-网-储一体化规划模型；文献［3］提出一种考虑灵活性的电力系统储能容量规划方法。当前低碳电力系统规划相关研究多以宏观统计法［4］或全生命周期法［5］统计电力系统碳排放量，这2 种方法均无法反映电力系统的网络结构与物理特性。而文献［6］所提出的碳排放流（carbon emission flow，CEF）分析方法可以实现碳排放在电力网络中的精确计量与时空溯源，揭示碳在产生、传输等过程中的机理与特性。如何从规划层面结合CEF分析方法探索未来清洁能源布局与低碳发展路径，仍需要深入研究。

当前新型电力系统规划研究缺乏“电视角”与“碳视角”的统筹兼顾，主要存在如下局限性。

1）当前灵活性规划在融合碳理念时，多以简单的非时变固定碳排放系数约束规划目标年的碳排放上限［7］，或根据联合国政府间气候变化专门委员会（Intergovernmental Panel on Climate Change，IPCC）颁布的各类燃料碳排放因子［8］进行碳排放水平评估，未结合电力网络物理特性进行碳排放精细化计量与追溯；另外，在研究高比例新能源带来的灵活性问题时，未考虑灵活性需求的多时间尺度特征，且未根据灵活性资源调节特性的差异优化资源出力以满足不同时间尺度的灵活性需求。

2）针对电力系统碳排放责任分摊问题，当前研究主要关注化石燃料类电源的直接碳排放责任，或者将碳排放责任转移至用户侧。针对源荷碳责任分摊问题，现有研究大多采用对半分摊原则［9］，或重点从需求响应角度考虑负荷侧碳责任［10］，发电侧只考虑直接排放型火电，但在未来新型电力系统中，风光等新能源的强不确定性与波动性可能导致其出力无法满足所在节点的实时负荷需求［11⁃12］，需由支路传递来自其他机组的电能，潮流传输过程中伴随着CEF，该部分额外碳排放若完全由负荷或其他火电机组承担则有失公平，因此有必要深入探讨新型电力系统中新能源机组的间接碳排放责任，研究将新能源考虑在内的源荷碳责任共同分摊机制。

针对以上问题，本文提出一种综合考虑新型电力系统低碳化与灵活性需求的灵活性资源规划方法：利用固有时间尺度（intrinsic time-scale decom⁃position，ITD）算法对灵活性需求进行多级分解，挖掘不同灵活性资源供给能力并进行灵活性供需匹配；基于潮流与CEF 理论将碳责任转移至包含新能源在内的源侧与荷侧，提出考虑碳责任因子的源荷双侧碳税机制；建立计及源荷碳排放责任的新型电力系统多级灵活性资源双层配置模型，上层模型对储能、抽水蓄能与燃气机组3 类灵活性资源容量进行投资决策，下层运行模型考虑多级灵活性供需平衡与源荷双侧碳税机制。最后，对改进的IEEE RTS-24 节点系统进行算例分析，验证本文所提规划模型的有效性与合理性。

1 新型电力系统多级灵活性供需平衡

新能源的波动性对系统灵活性需求的影响具有多时间尺度特征［13］。在高比例新能源场景下，传统电力平衡约束已无法满足对净负荷的实时包络，局部时段可能出现灵活性不足的情况，系统需调用灵活性资源以满足任一方向与不同时间尺度下的灵活性需求，即多级灵活性供需平衡，具体如下：

式中：Ftype，Δt为不同类型灵活性资源在不同时间尺度Δt下的灵活性供给能力；FD，Δt为系统在不同时间尺度Δt下的灵活性需求；PNL，t为t时刻系统净负荷；PL，t、PWT，t和PPV，t分别为t时刻系统负荷、风电和光伏的出力。

1.1 基于ITD算法的多级灵活性需求量化

本文采用ITD 算法对灵活性需求进行多级分解，分解净负荷波动曲线后得到的不同时间尺度分量对应于不同的调节速率要求。ITD 算法是一种自适应时频分解算法，与经验模态分解算法类似，ITD算法将原始信号分解成多个瞬时频率递减的适当旋转分量（proper rotation component，PRC）和1 个残余基线分量，但ITD 算法缓解了经验模态分解算法的端点效应问题，不存在筛选和样条插值过程，广泛应用于故障特征提取领域［14］。

结合电力系统中新能源波动特性和电源调节速率分布［15］，本文利用ITD 算法，将净负荷波动曲线分解成2 个PRC 和1 个基线分量，分别对应于灵活性需求的高频（＜15 min）、中频（15～60 min）与基频（＞1 h）分量：高频灵活性需求表示净负荷波动频率高，对应的时间尺度较小；基频灵活性需求表示净负荷波动平缓，对应于较长时间尺度灵活性。ITD 算法分解原理见附录A，分解效果如图1所示。

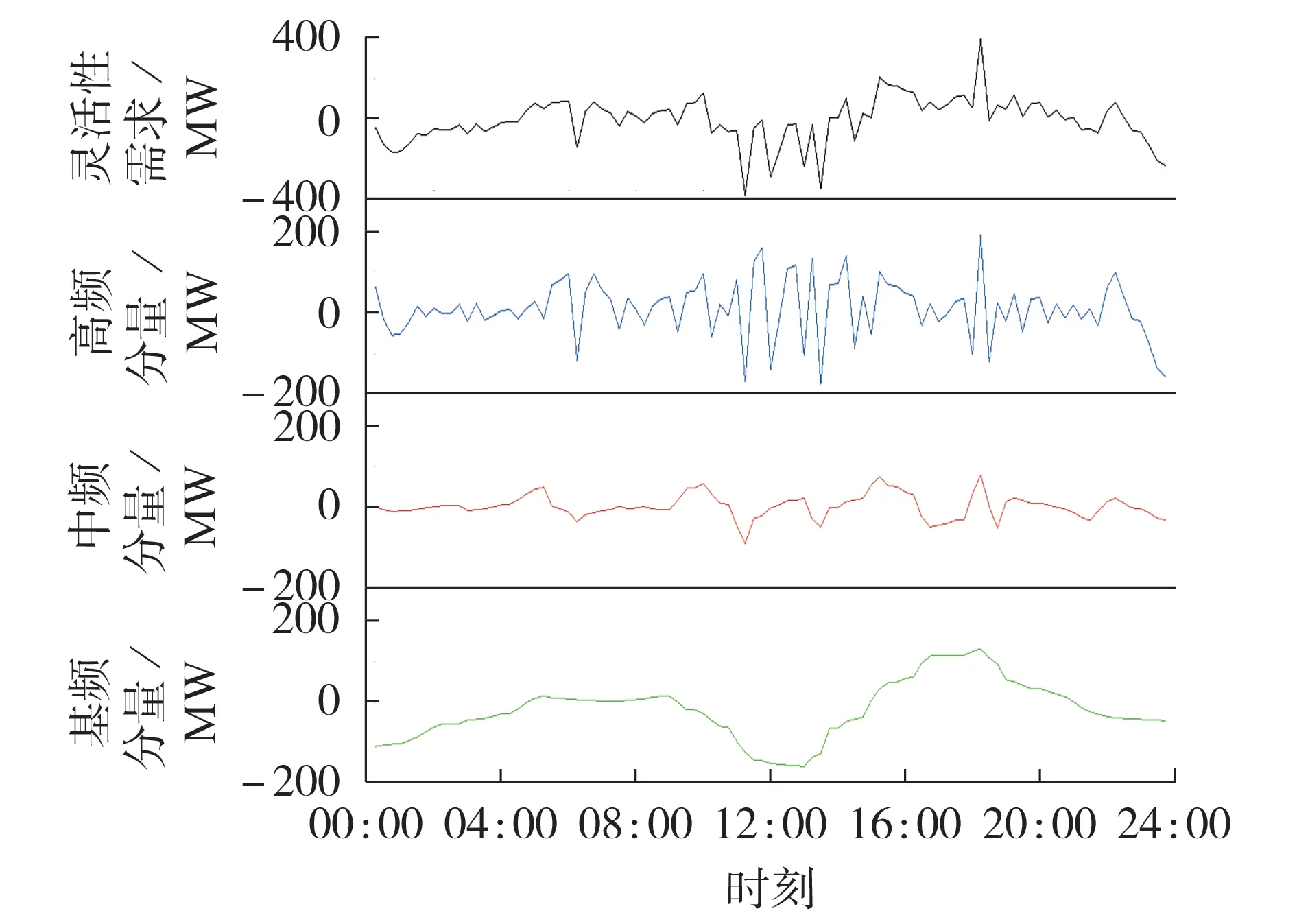
图1 ITD算法分解灵活性需求效果图Fig.1 Effect diagram of decomposing flexibility requirement based on ITD algorithm

1.2 多级灵活性资源供给能力分析

电力系统传统调节资源是火电机组，但其爬坡速率较慢，会产生大量温室气体，违背了低碳减排的初衷。在能源转型的驱动下，未来燃煤机组面临直接退役、超低排放改造、维持现状3 种选择。本文假设现役煤电在规划期内不会达到最大服役年限，但考虑一部分机组进行超低排放改造，其余维持现状，由多元灵活性资源平抑高比例新能源随机波动性，保障系统灵活性供需平衡。根据不同灵活性资源在调节方向、调节速率、可调容量等方面的差异，将灵活性资源与不同级别灵活性需求相匹配。

1）高频灵活性资源——电化学储能。

电化学储能属于功率型储能，具备快速响应能力，适用于满足高频灵活性需求。储能提供的灵活性由其充放电能力决定，为防止过度充放电，需要同时考虑储能系统运行周期内的剩余容量与各时刻的充放电功率［17］，储能灵活性供给能力如式（4）所示。

式中：F、F分别为不同时间尺度Δt下的电化学储能的上调和下调灵活性供给能力；Pdis，max、Pch，max分别为储能最大放电和充电功率；Pe，t为t时刻储能出力；Ee，t为t时刻储能电量；Ee，max、Ee，min分别为储能最大和最小电量；ηch、ηdis分别为储能充电和放电效率。

2）中频灵活性资源 —— 燃气机组。

相较于燃煤机组，燃气机组在效率、碳排放、最小技术出力等方面都具备优势，但其调节速率不及储能，考虑作为中频灵活性资源，灵活性供给能力如式（5）所示。

式中：F、F分别为不同时间尺度Δt下燃气机组的上调和下调灵活性供给能力；PG，max、PG，min、PG，t分别为燃气机组最大运行出力、最小运行出力和t时刻出力；rGT，up、rGT，down分别为燃气机组最大向上和向下爬坡速率。

3）基频灵活性资源——抽水蓄能电站。

抽水蓄能电站作为优质调峰资源可以提升新能源消纳能力，其作为能量型储能，可调容量大但响应时间较慢，适用于满足基频灵活性需求，灵活性供给能力如式（6）所示。

式中：F、F分别为不同时间尺度Δt下抽水蓄能电站的上调和下调灵活性供给能力；Pup，max、Pdown，max分别为抽水蓄能电站的最大发电和抽水功率；Pp，t为t时刻抽水蓄能电站出力；Ep，t为t时刻水库蓄水容量；Ep，max、Ep，min分别为水库蓄水容量上限和下限；η_f、η_c分别为抽水蓄能电站发电和抽水的能量转化效率。

2 基于CEF理论的源荷碳排放责任分摊

2.1 CEF基本理论

电力消费不直接产生碳排放，但消费侧的能源需求是源侧产生碳排放的驱动力。CEF 理论揭示了能量流中存在着碳排放的虚拟流动，将碳排放责任从化石燃料类电源转移至负荷侧，计量用户电力消费间接产生的碳排放量。表1 给出了电力系统CEF指标及其与潮流间的关系，这些指标构成了CEF 分析方法的理论基础［6］。

表1 电力系统CEF指标Table 1 Indices of CEF

2.2 考虑新能源的源荷碳排放责任分析

节点碳势是CEF 理论的一个重要指标，用于评估节点为满足负荷需求而引起的发电侧碳排放量，其值为所有流入节点的支路碳流密度关于有功潮流的加权平均值，即取决于注入节点的CEF 与潮流。设系统共有N个节点，则其碳势如式（7）所示。

式中：e为t时刻节点i的碳势；为潮流流入节点i的支路集合；Pl，t为t时刻流过支路l的有功功率；ρl，t为t时刻支路l碳流密度，其值为支路l的源节点j的节点碳势；P为t时刻节 点i所连 电 源的有功功率；e为节点i所连电源的发电碳强度（generation carbon intensity，GCI），由燃料的碳排放因子和消耗率确定；PNii，t为节点有功通量，其为N×N阶对角阵的元素，表示潮流方向下所有流入节点的有功功率之和。

节点所连机组类型包括常规火电、可再生能源与储能，需要分开讨论这3 类机组所在节点的碳势。火电机组由于自身GCI 值较高，因此所在节点碳势普遍较高，但具体取值还需根据式（7）计算，其值会随实时潮流与CEF 变化而变化。而风电、光伏等清洁能源的GCI 为0，即其自身发电不产生碳排放，但文献［11］和文献［12］算例结果显示，在未来高比例可再生能源场景下，可再生能源机组所在节点碳势并不为0，即该节点用户消费新能源电力所对应的碳排放量不为0。接下来重点讨论可再生能源机组与储能所在节点的碳势变化规律及其所需承担的碳排放责任。

2.2.1 可再生能源机组节点碳势与碳责任分析

风电、光伏等可再生能源机组的e=0，因此其所在节点碳势计算公式式（7）可以简化为：

由式（8）可知，可再生能源机组所在节点碳势与支路碳流密度、节点有功通量密切相关，结合节点负荷情况与碳势定义，分析不同条件下可再生能源机组所在节点碳势变化情况。

2.2.2 储能节点碳势与碳责任分析

储能具有源荷双重特性，其GCI 也为0，储能的充放电状态是影响其所在节点碳势的关键因素，下面分别讨论储能处于充电(Pe，t＜0)、放电(Pe，t＞0)与离网(Pe，t=0)状态下的节点碳势情况。

1）当储能处于充电状态时，储能出力为负，其潮流从节点流出，不再属于节点有功通量，被视为负荷，即节点负荷需求增大，此时需由其他节点输送更多的电能，因此储能需为该部分额外碳排放承担一定碳责任。储能所在节点的碳势计算公式变为：

2）当储能处于放电状态时，被视为电源，此时储能释放自身存储的电能，相当于降低了其他机组的出力与碳排放，具有低碳减排作用，因此该情况下储能无须承担碳排放责任。

3）当储能处于离网状态时，其所在节点碳势仅与流入节点的支路潮流和CEF 相关，碳责任由节点负荷承担。

2.2.3 源荷碳责任因子

本文在CEF 理论的基础上，考虑将碳排放责任分摊至源荷双侧，其中源侧除了传统火电，还包括可再生能源与储能。定义碳责任因子ξ∈[0，1]表示节点所连机组与负荷需分摊的碳排放责任。

1）对于连接火电机组的节点，规定源荷各自承担一半碳排放责任。

式中：ξFG，t为t时刻火电机组碳责任因子；ξL，t为t时刻负荷碳责任因子。

2）对于连接新可再生能源机组的节点，源荷各自承担的碳责任如下：

式中：ξRES，t为t时刻可再生能源机组碳责任因子。

3）对于连接储能的节点，源荷各自承担的碳责任如下：

式中：ξEES，t为t时刻储能碳责任因子；P为t时刻节点i储能的功率。

2.3 源荷双侧碳税机制

从征税对象而言，目前的碳税征收机制主要分为2类。

第一类规定由化石燃料类电源承担全部碳排放责任，根据电源的GCI值计算系统碳排放量，向发电侧征收碳税，该机制下碳税计算公式如下：

式中：Ccarbon为碳税；λcarbon为单位碳税价格；T为计算周期；ΩG为电源节点集合。

第二类规定由荷侧承担全部碳责任，可采用广义核仁、Shapley 值等多种方法分析负荷碳责任［19］，计算负荷侧应承担的碳税，碳排放量与碳税计算公式如下：

式中：ΩL为负荷节点集合。

本文利用CEF 模型追踪CEF 在电网中的足迹，以碳责任因子反映源荷双侧碳排放责任，将源荷所承担的碳排放责任量以碳税形式计算到运行成本中。计及可再生能源的源荷双侧碳税计算公式如下：

式中：ξG，t为t时刻电源碳责任因子；Ωn为负荷节点和电源节点集合。不同类型机组（火电、可再生能源或储能）的碳责任因子计算公式如式（10）、（11）、（13）所示。

3 新型电力系统灵活性资源双层规划模型

3.1 模型总体思路

本文建立考虑源荷双侧碳责任的新型电力系统多级灵活性资源规划模型，总体思路如图2 所示。上层模型以年综合成本最小为目标求解高比例风光渗透率下灵活性资源配置方案，年综合成本中的可变运行成本、碳税成本和灵活调节成本均由下层模型4 个典型日综合运行成本计算得到，将求解得到的资源配置容量传递给多级灵活性需求量化模型和下层优化运行模型。基于曲线形态聚类算法得到净负荷典型日及其对应天数，利用ITD 算法对灵活性需求进行多级分解，输入下层模型。下层以典型日综合运行成本最小为目标求解各资源的出力、灵活性资源的供给能力与节点碳势，将运行结果以各典型日综合运行成本形式反馈回上层模型的年综合成本中，上、下2 层迭代变量为各典型日运行参数，上层利用反馈结果对配置方案进行再次优化，如此反复迭代，得到最优配置结果。

图2 规划模型总体思路Fig.2 General idea of planning model

3.2 上层投资决策模型

上层投资决策模型的目标函数如式（19）所示。

式中：Cinv为年投资成本，其包括现役煤电超低排放改造投资成本C、新增风电场投资成本C、新增光伏电站投资成本C、新建抽水蓄能电站投资成本C、新建燃气电厂投资成本C和新建储能电站投资成本C；R为等值年投资折算系数；r为折现率，取8 %；y为规划年限；Copr为年运行成本，其包括年固定运维成本Cfopr和可变运行成本Cvopr，s，下标s表示典型日s；Ns为典型日数量；ξs为典型日s所占天数；Ccarbon，s和Cflex，s分别为典型日s的碳税成本和灵活调节成本。

式中：ΩCF、ΩWT、ΩPV、ΩPS、ΩGT和ΩESS为各类资源所在节点的集合；c、λ分别为煤电机组进行超低排放改造的单位容量投资成本和补贴金额；sg，0为煤电机组g初始容量；β为煤电机组g超低排放改造比例；c、c、c和c为各类资源的单位容量投资成本；sw，y、sv，y、sp，y和sG，y为 目 标 年 各 类 资 源 的 配 置 容 量；c、c分别为储能单位功率变流器配置成本和单位容量配置成本；Pe，y和Ee，y分别为目标年储能e配置额定功率和额定容量。

煤电、风电与光伏的年固定运维成本如式（31）所示。

式中：S、S和S分别为目标年煤电、风电和光伏的总容量，本系统煤电总容量与规划起始年保持一致，但其中有β比例的煤电容量进行了超低排放改造；c、c和c分别为煤电、风电和光伏的单位容量固定运维成本。

上层投资决策模型的约束条件除电力电量平衡约束外，还包括非水电可再生能源电力消纳责任权重约束和碳减排约束。

1）非水电可再生能源电力消纳责任权重约束。

式中：E、分别为目标年风电和光伏的发电量；Ey，D为目标年全社会用电量；κy，max、κy，min分别为权重上、下限；εloss为供电损耗率，取10 %。

2）碳减排约束。

式中：S为目标年超低排放改造的煤电容量；S为目标年未改造的容量；为常规煤电的GCI；e为超低排放改造煤电的GCI；SGyT为目标年新建燃气机组容量；e为燃气发电的GCI；σy为目标年碳减排比例；HCF，y为目标年煤电的年利用小时数；HGT，y为目标年燃气的年利用小时数；S为煤电的起始总容量；HCF，0为煤电的起始年利用小时数。

3.3 净负荷典型日聚类与灵活性需求分解

风电、光伏出力受天气、环境等因素影响，出力曲线呈较大波动性，而传统聚类算法多以欧氏距离作为样本相似度判据［20］，无法准确反映曲线形态的波动特征与相似程度。本文提出一种考虑多尺度和熵权法的曲线形态聚类算法［21］，通过4 种差分距离与分位数特征赋值得到多尺度差异测度，利用熵权法确定各尺度客观权重，得到差异测度矩阵，以曲线形态距离代替传统欧氏距离进行净负荷曲线聚类，聚类效果见附录B图B1。

上层模型确定风电与光伏初始配置容量后，结合某省级电网全年风光时序出力标幺值确定规划目标年风光出力情况，基于曲线形态聚类算法得到净负荷典型日及其对应天数，然后利用1.2 节所提ITD算法对灵活性需求进行多级分解，输入下层优化运行模型。

3.4 下层优化运行模型

下层模型分别对聚类得到的各个净负荷典型日进行优化运行，目标函数为日综合运行成本最小，包括煤电机组可变运行成本Cvopr，s、灵活性资源调节成本Cflex，s与源荷双侧碳税成本Ccarbon，s。

1）煤电机组可变运行成本。

2）灵活性需求的高频、中频与基频分量分别由储能、燃气与抽水蓄能供给，实现各级灵活性供需平衡，产生的灵活调节成本如式（36）所示。

式中：Fe，s，Δt、FG，s，Δt、Fp，s，Δt分别为不同时间尺度Δt下储能e、燃气机组G、抽水蓄能机组p的灵活性供给能力，各资源的灵活性供给能力如式（4）—（6）所示；、c、c分别为燃气、储能与抽水蓄能的单位灵活调节成本。

3）碳税成本。

利用CEF 模型实时计算各节点的碳势，根据2.3节所提源荷双侧碳税机制，计算典型日源荷双侧碳税成本为：

下层模型的约束条件包括电力平衡约束、煤电与燃气机组出力约束、储能运行约束、抽水蓄能电站运行约束和潮流平衡约束，具体表达式见附录C 式（C1）—（C19）。各级灵活性供需平衡约束如下：

式中：F、F和F分别为灵活性需求的高频、中频和基频分量。

4 算例分析

为验证本文所提规划模型的有效性，采用改进后的IEEE RTS-24 节点系统［22］进行算例分析。双层规划模型在MATLAB R2018a 软件中构建，下层模型采用MATLAB 的fmincon函数求解，该函数可用于求解非线性多变量规划问题的极值，上层模型调用遗传算法进行求解。

4.1 算例说明

设2021 年为规划起始年，选取2025 年和2030年为待规划年进行算例仿真。规划起始年系统负荷最大值为8 550 MW，按年增长率5.8 % 预测，煤电总容量为9 960 MW，风电和光伏容量分别为545 MW和365 MW，初始年系统风光渗透率仅为3.54 %。各机组的技术参数与经济参数参考文献［23］；根据碳税价格调查报告等资料［24］，将2025 年碳税价格定为65 元／t，2030 年碳税价 格 设 置 为93 元／t，煤电的GCI为0.74 6 t／（MW·h），经超低排放改造后煤电GCI 下降为0.671 4 t／（MW·h），燃气机组GCI 为0.441 t／（MW·h）。

4.2 新型电力系统灵活性资源配置结果

2025 年和2030 年新型电力系统资源优化配置结果如图3 所示。可见：相比于2020 年传统燃煤主导型电力系统，2025年和2030年风电与光伏成为主体电源，非水电可再生能源电力消纳责任权重均超过30 %；煤电分别按49.39 % 和69.57 % 的比例进行超低排放改造；为应对风光强不确定性与波动性带来的灵活性问题，配置了储能、燃气与抽水蓄能3 种灵活性资源，以满足系统多级灵活性需求。规划结果显示，本文所提规划模型可以推动传统煤电主导型电力系统向新能源主导型电力系统转变，在风光渗透率不断提高的同时，系统总碳排放量也大幅下降，但需要为新能源与灵活性资源的投资运行付出一定的经济成本，2025年与2030年规划方案的各项年经济成本如表2所示。

表2 规划方案的经济性成本Table 2 Economic cost of planning schemes单位：万元

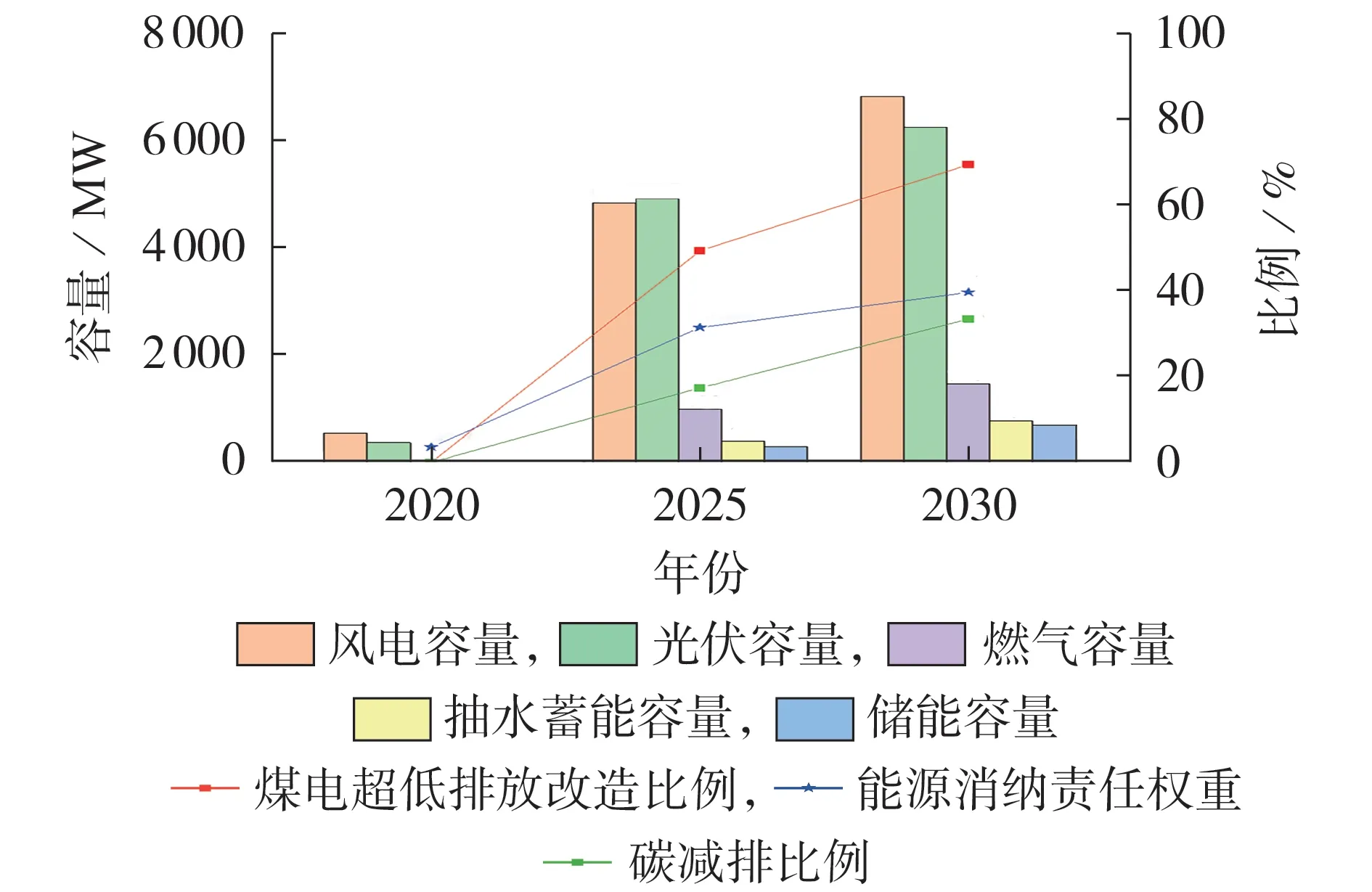
图3 优化配置结果Fig.3 Results of optimal configuration

4.3 典型日多级灵活性供需平衡分析

由于篇幅限制，故选取2025 年规划方案下4 个典型日优化运行结果中的一个进行分析，验证本文所提规划模型的运行灵活性。典型日电力实时平衡情况如图4 所示，多级灵活性供需平衡情况如图5所示。

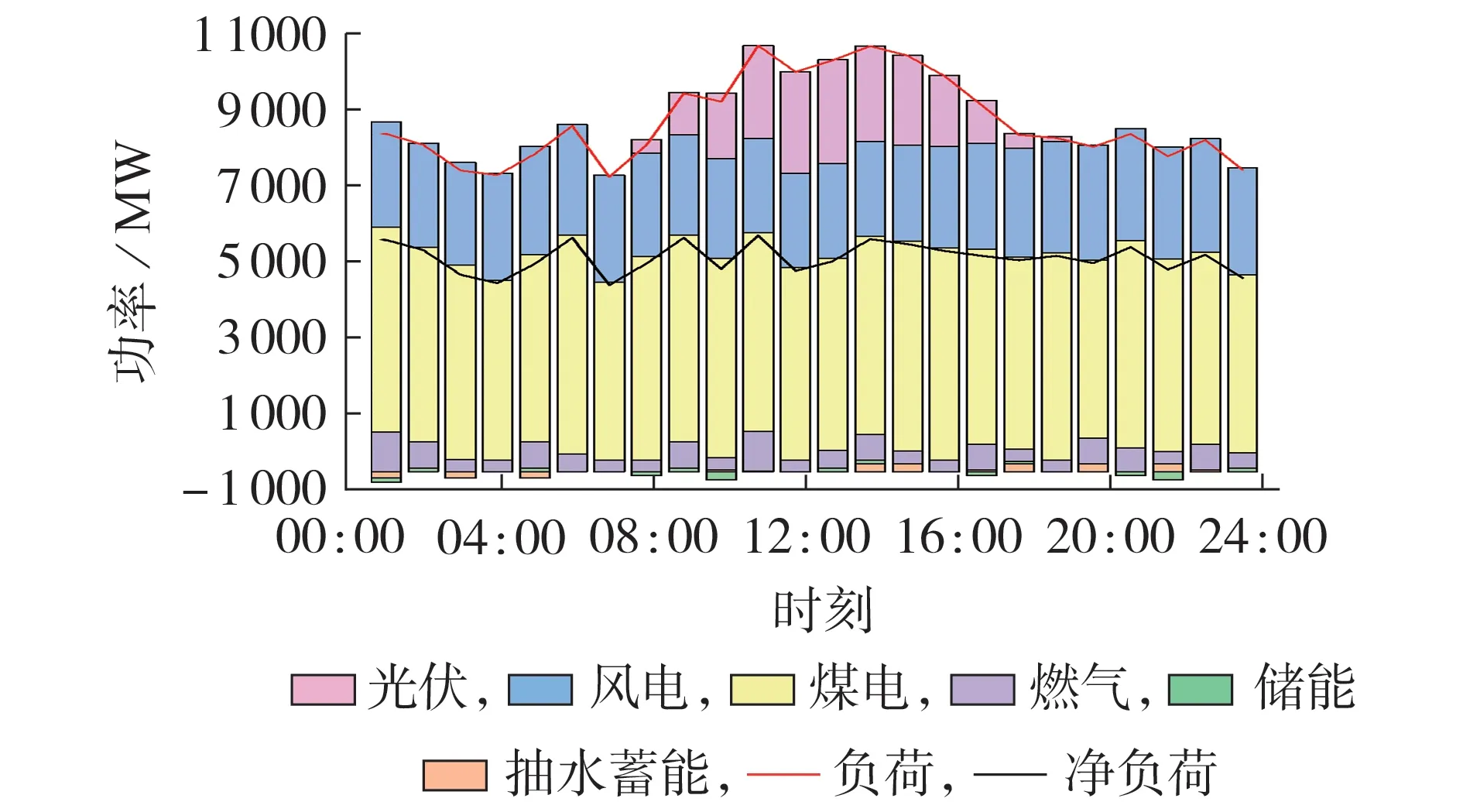
图4 2025年典型日电力实时平衡Fig.4 Real-time power balance on typical day in 2025

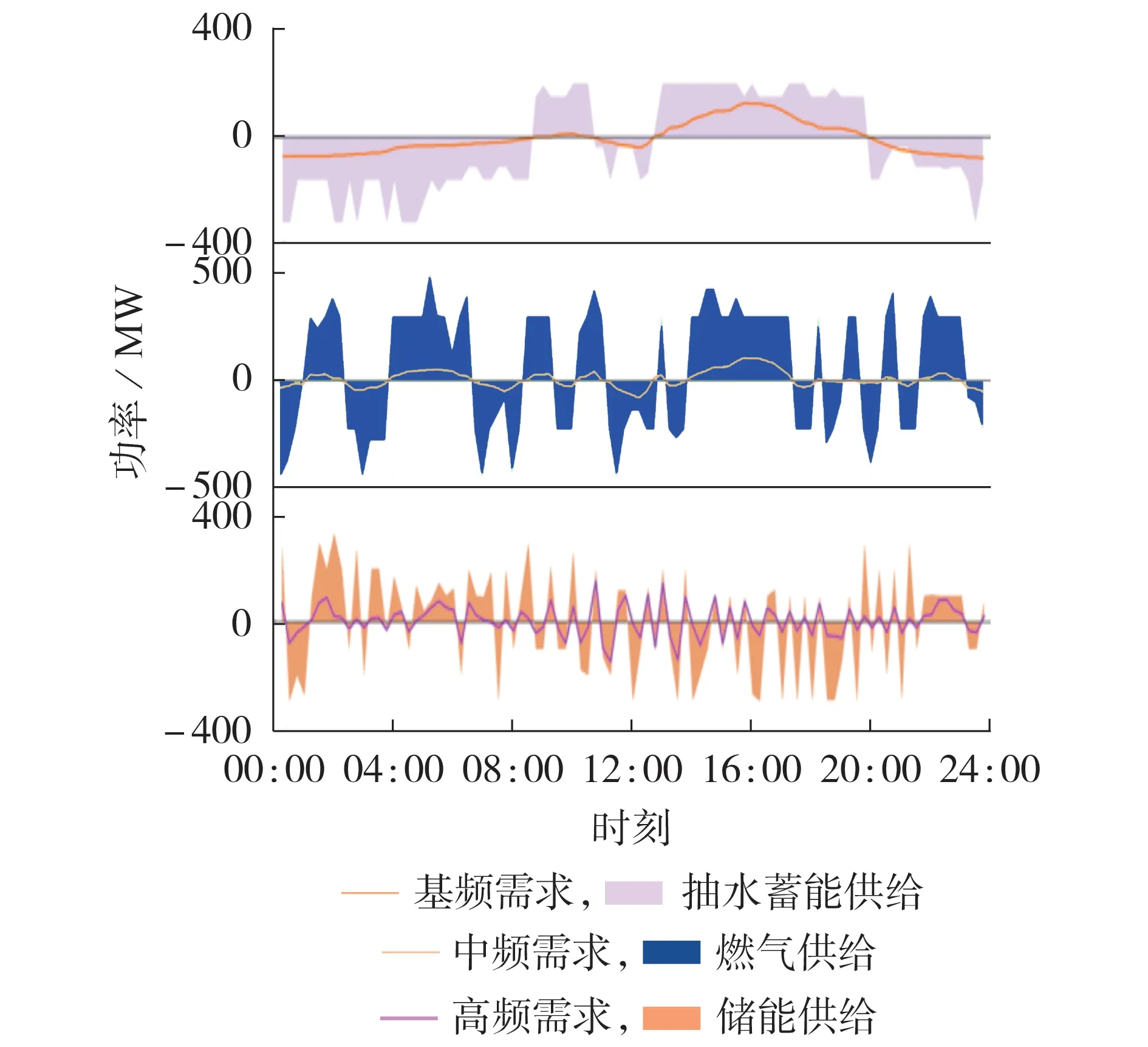
图5 2025年典型日灵活性供需平衡Fig.5 Flexible supply-demand balance on typical day in 2025

由图4和图5可知：本文所提多级灵活性资源优化配置模型可同时实现电力实时平衡与灵活性供需平衡，电力平衡侧重于实时功率平衡，灵活性供需平衡关注于功率的波动变化，二者共同保证了新型电力系统的灵活运行。图5 表明，本文所提规划方法可以实现由多元灵活性资源满足不同频段的灵活性需求：基频灵活性需求波动趋于平缓，时间跨度大，能量型储能具备长时灵活性供给的能力，抽水蓄能机组可在夜间负荷低谷期抽水以提供系统向下灵活性，在负荷高峰期发电以提供向上灵活性；高频灵活性需求波动明显，储能作为快速调节资源，可以及时响应并提供短期灵活性；中频灵活性需求介于基频与高频之间，可由燃气机组满足灵活性供需平衡。

4.4 基于CEF理论的源荷碳责任分析与验证

以2025 年规划方案下的一个典型日运行结果为例，分析不同类型电源所在节点的实时碳势，验证本文所提源荷双侧碳责任机制的合理性与优越性。系统拓扑与2025年规划结果见附录D图D1。

图6 展示了系统中典型节点碳势变化情况。由图可知：GCI为0的新能源机组所在节点的碳势并不为0，有些机组趋近于0，但有些机组较高，且随时间变化而变化；燃煤和燃气机组所在节点碳势普遍较高，接近自身GCI值。

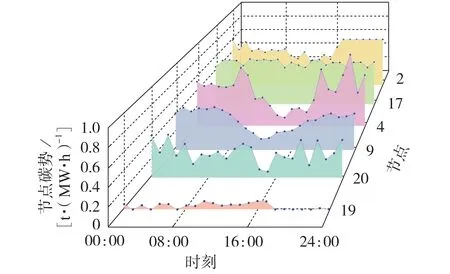
图6 节点碳势变化曲线Fig.6 Variation curves of bus carbon intensity

4.4.1 源荷碳责任分摊机制合理性分析

洛伦兹曲线是国际上用于反映一个国家或地区收入分配不平等程度的曲线，弯曲程度越大代表贫富差距越大。基尼系数是衡量该差距的指标，取值在［0，1］之间，其中取值小于0.2表示绝对公平，取值在［0.2，0.3）内表示比较公平，取值在［0.3，0.4）内表示分配合理，取值在［0.4，0.5）内表示差距较大，而取值在［0.5，1］内则表示差距悬殊［25］。

为验证本文所提基于CEF理论的源荷碳责任分摊机制是否公平合理，绘制节点碳税分摊的洛伦兹曲线并计算基尼系数。由于节点碳税的取值关键取决于源荷碳责任因子，而源荷碳责任因子又与节点碳势密切相关，因此将节点碳势（由低到高排序）的累积占比作为横坐标、各节点碳税的累积占比作为纵坐标，绘制洛伦兹曲线如图7 所示，基尼系数γ计算公式如式（41）所示。基尼系数计算结果为0.094 4，属于绝对公平范围，说明本文所提源荷碳责任分摊机制是公平的。

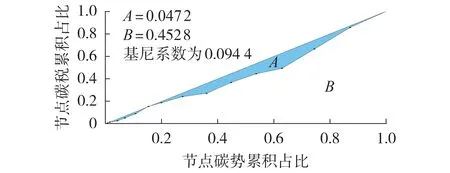
图7 源荷双侧碳责任分摊的洛伦兹曲线Fig.7 Lorentz curve of source-load side carbon responsibility

式中：A为洛伦兹曲线与45°均等线之间的面积；B为洛伦兹曲线以下的面积。

4.4.2 不同碳责任分摊机制对比

为验证本文在规划问题中考虑源荷双侧碳责任分摊机制具备低碳性与经济性，将不同碳责任分摊机制影响下系统的碳排放与碳税情况进行对比：机制1规定由化石燃料类电源承担碳责任；机制2规定由负荷侧承担碳责任；机制3 为本文所提的源荷双侧碳责任分摊机制。3 种分摊机制的碳税计算方法分别如式（15）—（18）所示，选取某个典型日运行结果进行计算对比，结果如表3和图8所示。

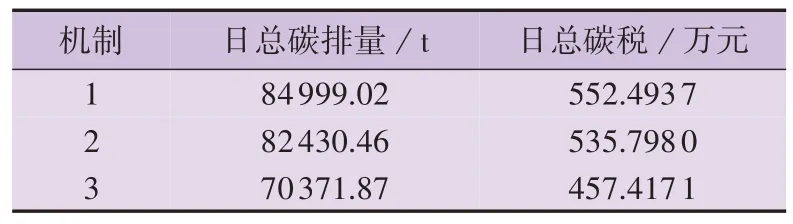
表3 不同碳责任分摊机制比较Table 3 Comparison of different carbon responsibility mechanisms

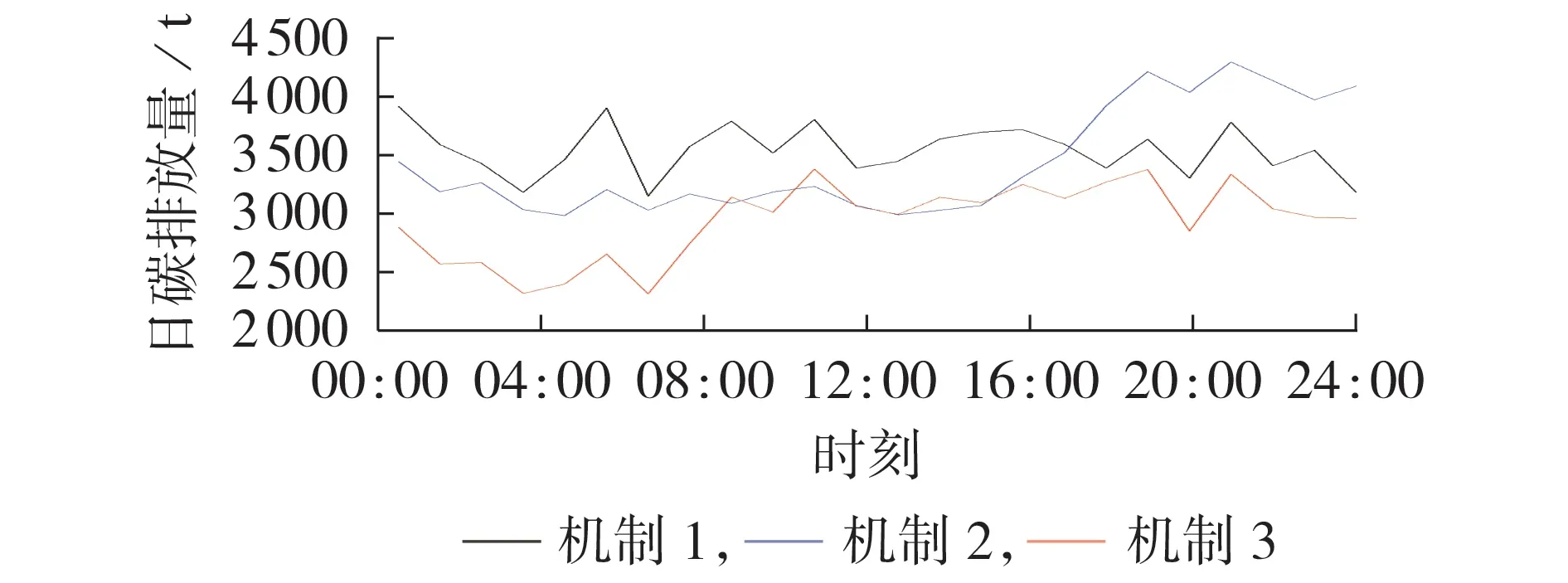
图8 不同碳责任分摊机制下系统日碳排放优化结果Fig.8 Optimal results of daily carbon emission of system under different carbon responsibility allocation mechanisms

由表3和图8可知：将本文所提源荷双侧碳责任分摊机制运用在新型电力系统优化运行与配置问题中，具备明显碳减排效果与经济性优势。大部分研究与实际工程均采用机制1，根据电源GCI值向火力发电侧征收碳税，即此时源侧碳责任因子为1，荷侧碳责任因子为0，但该分摊机制影响下的系统碳排放量较大，发电侧需缴纳较高碳税。机制2 考虑由用户完全承担碳责任，即此时荷侧碳责任因子为1，源侧碳责任因子为0，该机制在总碳排放量方面优于机制1，但存在用电高峰期用户需承担高额碳税的情况。而本文所提的基于CEF理论的源荷碳责任分摊机制，利用源荷碳责任因子将碳排放责任合理分摊至包含新能源在内的源荷双侧，应用在新型电力系统资源优化运行与配置问题中，可以有效抑制系统碳排放，还大幅减少了系统碳税成本，使源荷双侧公平合理地承担更少碳税。

5 结论

本文提出一种基于CEF理论考虑源荷双侧碳排放责任的新型电力系统多级灵活性资源规划方法，通过算例仿真与结果分析得到如下结论：

1）本文将多级灵活性供需平衡约束作为“电视角”下灵活性规划问题的内因驱动，源荷双侧碳责任分摊机制作为“碳视角”下低碳规划问题的外力驱动，内因与外力共同驱动传统燃煤型电网向新能源主导型低碳电网转变；

2）本文提出基于ITD 算法的灵活性需求多级分解方法，可以反映新能源波动性对系统运行造成的多时间尺度影响，不同级别灵活性需求与不同灵活性资源相对应，有效区分不同资源调节速率与能力的差异，充分发挥不同灵活性资源供给能力，在运行层实现多级灵活性供需平衡；

3）本文基于新型电力系统潮流与CEF分析结果提出源荷碳责任因子，可以将碳排放责任合理分摊至包含新能源在内的源荷双侧，双层规划模型中考虑源荷双侧碳税成本可以有效抑制系统碳排放，优化资源配置，满足新型电力系统的低碳化需求，推动新能源在电力系统中的高度渗透。

后续考虑将灵活性需求多级分解与基于CEF理论的源荷双侧碳责任分摊机制应用于综合能源系统规划运行问题中。

附录见本刊网络版（http：//www.epae.cn）。