Sequential Inverse Optimal Control of Discrete-Time Systems

Sheng Cao , Zhiwei Luo , and Changqin Quan

Abstract—This paper presents a novel sequential inverse optimal control (SIOC) method for discrete-time systems, which calculates the unknown weight vectors of the cost function in real time using the input and output of an optimally controlled discrete-time system.The proposed method overcomes the limitations of previous approaches by eliminating the need for the invertible Jacobian assumption.It calculates the possible-solution spaces and their intersections sequentially until the dimension of the intersection space decreases to one.The remaining onedimensional vector of the possible-solution space’s intersection represents the SIOC solution.The paper presents clear conditions for convergence and addresses the issue of noisy data by clarifying the conditions for the singular values of the matrices that relate to the possible-solution space.The effectiveness of the proposed method is demonstrated through simulation results.

I.INTRODUCTION

THE standard optimal control problem concerns finding the state and input trajectories for a dynamical system.In this regard, the inverse optimal control (IOC) approach is generally employed to obtain the weighting parameters of the cost function using the input/output data generated by optimal control.

In many fields, such as robotics [1], biological systems [2],[3] and marketing systems [4], the optimization of the systems’ behavior has been studied using the IOC method.

In [1], a method is proposed to estimate the cost function of human operators for human-robot interaction control.The IOC method was utilized in [5] to analyze the route choices of taxi drivers.To evaluate the cost combination of human motion, in [6], the IOC method was utilized to analyze the reaching movement of the human arm.Furthermore, biological behavior has been modeled as an inverse linear quadratic regulator problem, and an adaptive method was proposed to model and analyze human reach-to-grasp behavior by [7].

As mentioned in the literature, there are two main groups of IOC.One has a hierarchy structure that updates the cost function in the higher stage while the forward optimal control problem is repeatedly solved in the lower stage to minimize the evaluation function between the original data and the generated data.In [8], where the IOC problem is formulated by another form (the inverse-reinforcement-learning method),cost weights are adjusted to better evaluate the observationfeature values and maximize the entropy of the trajectoryprobability distribution.When considering the IOC problem as a special bilevel optimal control problem [9], where the lower level is the optimal control problem and the upper level is the inversion problem, the IOC problem has been considered for simple dynamical models [10].To analyze locomotion movements, the authors of [3] proposed a bilevel optimization method based IOC method.In [11], mathematical programs with complementary constraints in the context of the IOC method are discussed for the application of locomotion analysis.In [12], the bilevel optimization problem for IOC is transformed into a single-level problem, and a globally optimal solution is computed.Although these methods are effective and have been utilized in many applications, such as human-motor behavior analysis, robot navigation, and autonomous driving, they require significant computational costs in the lower stage to repeatedly verify the updated cost function.

Conversely, the second class of IOC research focus on solving this problem by exploiting several optimality equations,such as Pontryagin’s maximum principle-based equations[13], and Euler-Lagrange equations [2].In [14], a linear combination of feature functions with unknown weight parameters was formulated to approximate the original optimal cost function.In [15], the recovery of the weight parameters of the finite-horizon, discrete-time optimal control was considered.For practical applications, it is important to obtain the cost weights in real time.In [16], a method is proposed for the online calculation of discrete-time IOC in both finite and infinite horizons; however, it requires the invertibility condition of a Jacobian.In addition, the convergence of the cost weights has not been theoretically investigated.

Control Lyapunov function (CLF) based IOC is an essential paradigm in control theory, where a stabilizing feedback is designed first and then shown to be optimal for a cost function.In recent years, there have been numerous contributions to address the limitations of CLF-based IOC.The extended Kalman filter (EKF) has been utilized in some studies to construct a CLF [17], [18].Furthermore, some researches have applied CLF-based IOC to non-linear inverse optimal control problems [19].Additionally, some works have developed data-driven non-linear stabilization schemes utilizing the Koopman operator [20], and focused on learning simple polynomial CLFs from counterexamples and demonstrations for non-linear dynamical systems [21]-[23].Despite these advancements, notable limitations of CLF-based IOC method persist, including the inability to explicitly specify a clear optimal cost function and the difficulty in selecting and adjusting parameters, which often requires extensive experience and expert knowledge.

Moreover, the problem of noisy data is a source of concern in IOC research.The authors of [24] analyzed the IOC problem for discrete-time finite-horizon LQR as an optimization problem and proved that the solution to the problem is statistically consistent.They utilized the data from multi-observations to complete the offline IOC method.In [25], building on the work of [24], the authors recast the IOC problem as the identification of a parameterized causal and anti-causal mixed system exited by boundary conditions.They clarified sufficient identifiability conditions for the unknown parameters in terms of the system model.Besides, [26], [27] also emphasize the consideration of data noise.Although the aforementioned methods are effective in tackling problems of noise for the offline IOC problem of discrete-time finite-horizon LQR, it is still necessary to consider the noisy problem in the IOC method in (1) online calculation and (2) nonlinear system’s IOC method.

This paper proposes a novel SIOC method to address the issues mentioned above.The method recovers the cost function of an optimal control problem from input/output data acquired step-by-step, and solves the inverse optimal control problem sequentially with a promised convergence speed.By assuming the positivity of a Jacobian, this method is applicable even if the invertible Jacobian assumption required in [16]is not satisfied.Most importantly, the method clarifies the conditions for the convergence of the weight estimation in every step, which can be utilized in the analysis of real applications.On the other hand, in this study, the noisy data problem is considered for the online recovery of the cost-weight vector.We also analyze the effect of noisy data on the possible-solution space and propose a one step selection method of the possible-solution space for the noisy case using noisy data from multiobservations.Contribution of this research comes from three aspects.

1) The first contribution is the promised solution’s calculation speed and the conditions that enable it.We discuss the conditions for the decrease in the dimension of the intersection space.Consequently, if any of the conditions listed (Theorem 1) is satisfied, the dimension of the intersection of the solution’s space will decrease in each step, allowing us to obtain solutions within a promised number of steps.This is beneficial for applications that require high-speed calculations.

2) The second is the establishment of a sequential IOC method without utilizing the invertible Jacobian assumption in[16].Notably, although the invertible Jacobian assumption is widely used in the solution of the forward finite and infinite horizon optimal control of the discrete system, as highlighted in ([28]), some necessary conditions are proposed to apply the method for the system dynamics even if the invertible Jacobian assumption is not satisfied.

3) The third is the development of an efficient method for tackling the noisy data problem in the online IOC calculation.If we have prior knowledge of the maximum error value, we can analyze the effect of the error on the possible-solution space in our method and propose two conditions for selecting the possible-solution space.Simulation results show that this method is effective.

II.PROBLEM FORMULATION

Consider the dynamics of a discrete system

In our problem, we assume thatx[0,K]as well asu[0,K]constitutes a solution to minimize (2) for system dynamics (1).The objective of this research is to realize the online estimation of the cost weight vectorqin cost function (2), i.e., to calculate vectorqonline for the given system statexkand the control inputukwithout the storage and batch processing.The time horizonKis known priorly.

III.SEQUENTIAL IOC FOR THE NOISE FREE CASE

In this section, we introduce the maximum principle for the finite and infinite horizon, optimal control problems, which is applicable when any condition provided in Assumption 1 is satisfied.Based on the introduced maximum principle, we propose a sequential IOC method.

A. Maximum Principle for the Finite and Infinite Horizon Optimal Control Problems

The Hamiltonian function associated with the optimal control problems given by (1) and (2) is defined as

In [28] (Theorems 2.2 and 2.6), it has been shown that both the assumptions of Jaocbian’s invertibility (Assumption 1-1))and positivity (Assumption 1-2)) can be used to establish Pontryagin’s maximum principles in both finite and infinite horizon discrete-time optimal control problems.These assumptions are especially necessary for infinite horizon problems.While the previous study [16] of online IOC assumed Jacobian’s invertibility to establish the discrete-time maximum principle, this assumption may not hold for some system dynamics.Therefore, the Jacobian’s positivity assumption(condition) is proposed in [28] as an alternative to the invertible assumption (condition).For example, it suffices to consider the case where for allni,njto see that Assumption 1-2) is fulfilled andis not invertible since its rank is equal to 1.

In addition, as in [16], the inactive constraint times of the control input are defined as

Definition 1:Given the control input,uk, fork＞0,

is defined as the set when the control constraints are inactive.Here l represents time larger than 0, and int(U) denotes the interior of the inactive control constraint set, U.

Based on [16], [28]-[30], for the above assumptions and definition, the following lemma holds:

Lemma 1: Suppose that the optimal control problems defined by (1) and (2) are solved by trajectoriesx[0,K]andu[0,K]and if the Assumptions 1-1) or 1-2) hold, then there exist co-state vectors λ0,...,λKthat satisfy the combined Pontryagin’s maximum principle as

B. Construction of the Sequential IOC Method

Proof: The proof of this theorem is shown in Appendix.■

Therefore, if Conditions a) or b) of Theorem 1 is satisfied,the dimension of the intersection of the possible-solution space will decrease in every step.

C. Calculation of Vector sh

1)Calculation of the Intersection Space: Here, Ωsis the matrix related to the intersection of the possible-solution spaces, which is initialized in stephand is updated in every cycle.

We halt the calculation when the control constraint is active and reinitialize, restart the IOC calculation when it is inactive.The high calculation speed of our method makes it possible to quickly complete the IOC calculation after the active duration of the control constraints so that it is not necessary to store the data of the duration before the control constraints are active[16].

The total calculation in the noise-free case is shown in Algorithm 1.

IV.WHEN NOISE EXISTS

When measurement noise or numerical errors exist, the noisy-system state,xˆ, and control input,uˆ, introduce errors into the calculation of Φh(i), resulting in the deviation of the calculated possible-solution space from the correct result.Here, we also introduced a method for tackling this problem.

First, in this research, we assume that the noise of the measuredxˆ anduˆ satisfies the following conditions:

where ϵxand ϵuare two positive scalars.Furthermore, we introduce the following assumption of the system dynamics and feature function.

Algorithm 1 Online Implementation (Noise-Free Case)Input:xi,ui,||q||Output:Initialization :Hh Φh(h)sh 1: Compute a and.Ωs=Φh(h)2: Initialize matrix which represents the intersection of possible-solution spaces.LOOP Process i=h+1 3: for to K do ui ∈int(U)4: if then ui-1 ∉int(U)5: if then Φh(i) Ωs=Φh(i)6: Calculate and reinitialize 7: Continue.8: end if Φh(i)null(Φh(i)) null(Ωs)9: Calculate , and.ΓΩs ∩ΓΦh(i)Yh(i)=[null(Φh(i))T,null(Ωs)T]T Yh(i)ΓΩs Ωs 10: Calculate by constructing the matrix and compute the null space of.Here, denotes the vector space of.rank(Yh(i))＜N-1 11: if then Ωs=null(Yh(i))12: Update 13: end if rank(Yh(i))=N-1 14: if ( ) then Ωs Ωs=null(Yh(i))15: is decreased to a vector with.16: Get the unique solution following (19).17: end if 18: end if 19: end for sh 20: return

Assumption 2: Functionf¯u(k),f¯x(k),F¯u(k),F¯x(k)satisfy

Algorithm 2 Online Implementation (Noise Case){xi,ui}is,||q||Input:Output:Initialization :sh His h Φis h(h) {x,u}is T1ˆΦh(k),...,1: Compute and using and reconstruct.Ωs=ToˆΦh(h)2: Initialize matrix following (51) which represents the intersection of possible-solution spaces.LOOP Process i=h+1 TisˆΦh(k)3: for to K do¯ui ∈int(U)4: if then¯ui-1 ∉int(U)5: if then ToˆΦh(i) Ωs=ToˆΦh(i)6: Calculate and reinitialize 7: Continue.8: end if ToˆΦh(i)null(ToˆΦh(i)) null(Ωs)9: Calculate , and.10: Calculate by constructing the matrix and compute the null space of.Here, denotes the vector space of.rank(Yh(i))＜N-1 ΓΩs ∩ΓToˆΦh(i)Yh(i)=[null(ToˆΦh(i))T,null(Ωs)T]T Yh(i)ΓΩs Ωs 11: if then Ωs=null(Yh(i))12: Update 13: end if rank(Yh(i))=N-1 14: if ( ) then Ωs Ωs=null(Yh(i))15: is decreased to a vector with.16: Get the unique solution following (19).17: end if 18: end if 19: end for 20: return sh

3)Calculation With Control Constraints: When there exist control constraints and noise in data , we replace the calculation procedure for the control constraints with

whereu¯irepresentsthemean value of the control input of the multipledata series{x,u}is.

V.SIMULATION EXAMPLES

We perform several simulations in different cases to verify the effectiveness of our method.

To ensure the reproducibility of the calculation process, we reinitialize a new IOC calculation cycle in all simulations after obtaining a result in stepi.This also allows us to verify the performance of the algorithm under different initial conditions, as the initial state at the start of each new calculation cycle of SIOC will be different from the previous one.

A. Simulation 1: Comparison With [16]

This section illustrates our method with simulation in the settings of nonlinear system.The system dynamics are

We recover the cost weights in (56) and compared the simulation results with the results of [16] according to two aspects:the number of time steps required to recover the cost weight vectors in each cycle (Figs.1 and 2) and the recovery error of the cost weights (Figs.3 and 4).

Fig.1 shows the result of the step performed in our method,while Fig.2 shows the result in [16].The horizontal axes in both figures represent the total steps during the simulations.The dotted blue line is the end of each cycle while its height related to the left vertical axis is the number of steps spent in each IOC cycle.The red lines in these two figures represent the dimension variation of the intersection of the possiblesolution spaces whose value relates to the right vertical axis.

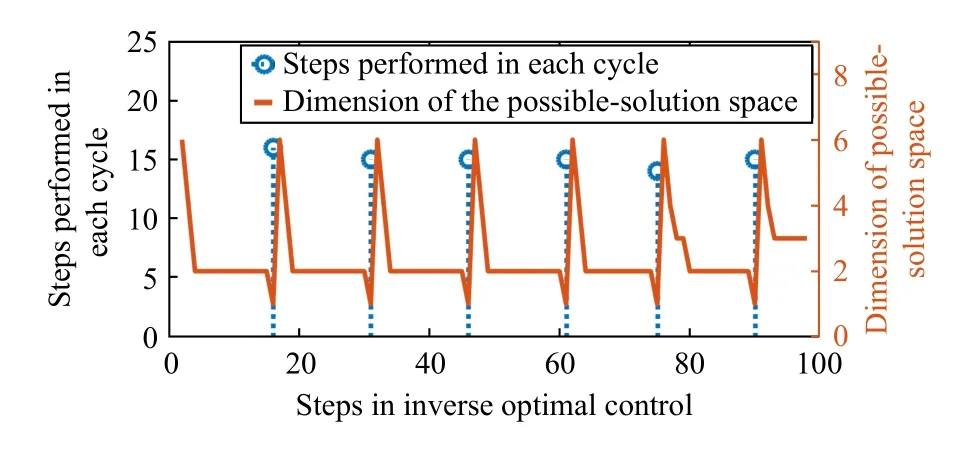
Fig.2.Steps performed in method of [16] for Simulation 1 are shown here.The meaning of the lines is the same as in Fig.1.

Fig.3.Recovery errors of Simulation 1 by our method are shown here.The blue circles represent the recovery error in each IOC cycle.

Fig.4.Recovery errors of Simulation 1 by [16] are shown here.The meaning of the lines is the same as in Fig.3.

The result in Fig.1 shows that the dimension of ΓΩh:idecreases in every step in each calculation cycle and that the maximum number of steps in one cycle is 1.Compared with our result, the dimension of the possible-solution spaces in[16], does not decrease continually.As a result, the number of steps of one cycle for [16] in Fig.2 is always larger than that in our method.

Figs.3 and 4 show the recovery error of both methods calculated bye=||qˆ-q|| w hereqˆ denotes the estimation vector ofq.From these two figures, it is clear that the estimation error of our method is minor.Therefore, our proposed method can effectively improve the calculation speed while preserving the recovery accuracy of IOC.

B. Simulation 2: When Jacobian is not Invertible

In Simulation 2,

Here, the system matrix,A, does not satisfy the Jacobian’s invertibility assumption, but it satisfies the Jacobian’s positivity assumption.In this case, [16] cannot be applied.The cost function selected in the simulation is

Fig.5 shows the calculation steps in every cycle, which is 1.Here, similarly to the result obtained in Simulation 1, the variation in the dimension of the possible-solution spaces verifies Theorem 1, and the variation in the dimension of the possiblesolution spaces after the activation of the control constraints shows that the proposed algorithm is effective for handling the control constraint problem.

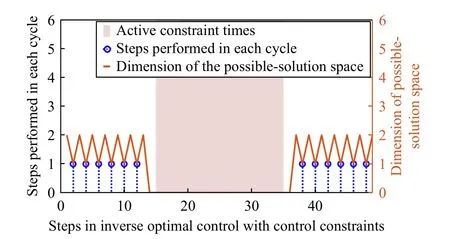
Fig.5.Steps performed in our method for Simulation 2 are shown here.The meaning of the lines is the same as in Fig.1.

Fig.6 shows the estimation error in this simulation.Even whenAis rank deficient and control constraints exist, the errors in all cycles are still extremely small, which shows that the proposed method can effectively recover the required cost weights with considerable accuracy.

Fig.6.Recovery errors of Simulation 2 by our method are shown here.The meaning of the lines is the same as in Fig.3.

Fig.7.Comparison of original trajectories (system states and control inputs) with the trajectories using recovered cost weights.

Fig.7 shows a comparison between the original trajectories of system states and control inputs and the trajectories generated using the recovered cost weights.The red and blue lines in the figure are identical, indicating that the recovered cost weights can be used to replicate the original optimal trajectories.This demonstrates the potential of our method to be further applied in demonstration tasks.

C. Simulation 3: Verification of SIOC Under Different Conditions

In Simulation 3, we conducted a comprehensive evaluation of the proposed SIOC method under different initial conditions and system dynamics.Specifically, we simulated 1000 different linear systems with randomly generated initial states(x0) and system matrices (AandB).All system settingsAandBused in our simulations were randomly generated using the MATLAB functionrand(3,3) forAandrand(3,2) forBand the initial states were generated using 1 0×rand(3,1).For each system, we applied the SIOC method and evaluated its performance in recovering the cost weights.Fig.8 shows the recovery errors of the SIOC method performed with 1000 different system dynamics and initial states.The results demonstrate that the recovery errors are consistently very small (average error of 4.0312×10-15), indicating the effectiveness of our method.

D. Simulation 4: When There Exists Noise

Due to the decaying property of the state sequence and the stationary property of the measurement noise, the signal-tonoise ratio (SNR) is defined as

Fig.8.Verification of SIOC under different conditions (1000 different system dynamics and initial conditions).

wheretFrepresents the time index at which the IOC calculation is terminated.To verify the effectiveness of our method,we performed simulations at several noise levels.In simulations at each noise level, we performed simulation 100 times with different system dynamics.Here, we performed simulations on linear systems withA∈R3×3andB∈R3×2randomly selected using matlab functionrand().The initial state is randomly selected, and noises at different SNRs are generated following the standard Gaussian distribution.

Fig.9 shows the comparison results between our method and that in [16] withS NR= values of 20, 65, 94, 191, and 238, respectively.There are 100 results in comparison study of eachS NR’s settings.In the simulations, the estimation error is evaluated by relative-estimation error, defined as.

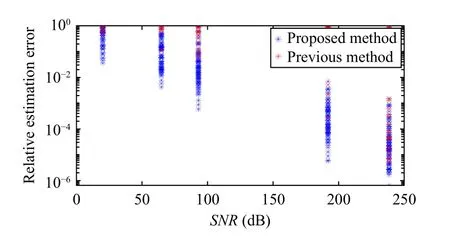
Fig.9.Comparison of our method (blue points) with the method in [16](red points) under noisy conditions.1) SNR = 20, 65, 94, 191, 238; 2) There are 100 simulation samples in each selection of SNR.

From Fig.9, it is clear that in our method, the relative-estimation errors decrease along with the increase in the SNR,indicating that this noise-tackling method can be utilized in the noise-free case.Moreover, a comparative study with the method in [16], revealed that our SIOC method considering noises is more robust in each setting of SNR.

Therefore, from Simulations 1 and 2, it is verified that the proposed method can solve the online IOC problem even for the systems that are not applicable in [16].Our method effectively improves the calculation speed of IOC.From Simulation 4, it is evident that the proposed method can effectively tackle the noise problem, which is not considered in the previous online IOC study.

VI.DISCUSSION

A. Computation Complexity

The computational complexity of our method in one step isO(3(n+nf)3+(n+nf)n′2+(n+nf)(n+nf+n′)2)in the noisefree case, wheren′is the dimension of the possible-solution space and it decreases as the step number increases.The computational complexity of our method does not contain horizonK, it is typically less than that in [15], wherein the horizonKwas contained in the computation-complexity calculation.Conversely, the computational complexity of [16] isO((n+nf)3+m(n+nf)2)in one step.

We conducted simulations using 1000 different system settings and initial states, and compared the calculation time of our method with that of the previous method.The results, presented in Fig.10, show that while our method has a slightly longer calculation time in one step than the previous method[16] on average, it is more stable, with less variability in the calculation time across the different system settings and initial states.Notably, our method requires fewer computational steps, and therefore, the choice of the method with lower total computational complexity may depend on the specific case.

Fig.10.Calculation time in one step under different conditions (1000 different system dynamics and initial conditions): Our method versus previous method [16].

B. Importance of the Sequential Calculation of the IOC Method

This paper proposed a sequential inverse optimal control IOC method that derives the conditions of the possible-solution space and tackling method for noisy data.

The first advantage of SIOC is that it saves computational time.This is a significant advantage for programs that require real time computing.

Secondly, there is no assurance that the cost weights will remain constant across all the previously well-selected feature functions while studying the complex dynamic movements.In[31], the authors suggested a method for calculating the multiphase cost weights based on window shifts, and when using this method to study complex motions, the length of the window must be minimized to recover the cost weight with multiphase changes in high precision.In this case, our SIOC method can be used to reduce the length of the window.

Additionally, the high calculation speed of the SIOC strategy helps to lessen the impact of noise.Notably, achieving noise reduction in the analysis of the observations from different steps is challenging, and this process must be completed for the calculation of each different IOC method.The impact of noise increases with the accumulated data step by step.The method proposed introduces a calculation method for the IOC with a minimum number of steps, and this high calculation speed helps to reduce the effect of noisy data on the final costweight estimates.

C. Future Work

Although the problem of sequential IOC has been solved in this study considering the calculation speed and noisy data,the algorithm still requires improvement in the following areas.

1) It is possible to further improve the noisy-tackling ability in the sequential IOC method.Since this method has a high convergence speed, we can start an IOC calculation cycle at each step and obtain time-series groups of solutions.By theoretically analyzing the result in each calculation cycle and considering the effect of the multiphase cost weight, it may be possible to further enhance the precision of the estimation result.We will also address the matter of special system dynamics in real-world application examples where the system states exhibit insensitivity to changes in cost weights.This insensitivity magnifies the effect of noise on the accuracy of the IOC calculation in noisy scenarios.

2) It is also required to discuss the selection of the feature function.To analyze the complex nature behavior, the selection of the feature function will highly affect the approximation results.Additionally, the aforementioned problem of multiphase cost weights is highly related to the selection of the feature function.

3) In addition, while the SIOC method proposed in this study solves the online recovery of the cost function, further investigation could be undertaken to develop effective and efficient algorithms for online tuning of the control input,especially crucial in control problems where minimizing a specific cost function is challenging or selecting suitable cost weights poses difficulties.

VII.CONCLUSION

A sequential method for discrete-time IOC is presented in this paper to realize the online estimation of cost weights for either finite or infinite horizon optimal control in cases with significant data noise.This method calculates the possiblesolution space of the IOC and sequentially calculates the intersection of all solution spaces in each step.The conditions for the decrease in dimension of the intersection space in the noise-free case are clarified first.When the dimension of the possible-solution space decreases to one, the remaining vector in the intersection space is the required solution of the cost weight of the IOC.In the noise case, an adjusted calculation of the possible-solution space is proposed based on the analysis of the noise effect.Finally, simulation results illustrate that the sequential IOC algorithm is effective, has a high convergence speed, and can sequentially tackle the problem of noisy data.More theoretical studies on the influences of the feature function selection on the solution spaces should be conducted for practical applications.

APPENDIX PROOF OF THEOREM 1