基于双折减系数法的重力坝抗滑稳定性研究
张秀琴,傅小孙,王会学
(1.山东硕庆工程项目管理有限公司江西分公司,江西 南昌 330038;2.新余市水利电力建筑工程有限公司,江西 新余 338000;3.中国安能三局成都分公司,四川 成都 641000)
1 引言
强度折减法是重力坝抗滑稳定分析时的常用方法。但目前关于双折减系数法的研究大多集中于边坡稳定性研究方面,双强度折减法在重力坝抗滑稳定性研究中的适用性和规律性如何还鲜有学者进行研究。本文以我国西南某重力坝为研究对象建立坝体-地基三维仿真模型,基于双折减系数法研究该重力坝在设计地震作用下的抗滑稳定性问题,以期为重力坝抗滑稳定性研究提供参考。
2 计算原理
2.1 双折减系数法
双折减的关键就是根据岩土体结构失稳破坏的实际情况对粘聚力c 和φ内摩擦角进行非等比例折减,为此,唐芬[1]提出了折减比的概念,即折减比r=k1/k2,其中k1、k2分别为共同折减过程中内摩擦角φ和粘聚力c 的折减系数,双折减法始终围绕折减比r 来进行,具体实施过程如下:
(1)保持粘聚力c 不变,只折减内摩擦角φ直到重力坝滑动失稳得到。
(2)保持内摩擦角φ不变,只折减粘聚力c 直到重力坝滑动失稳得到。
(3)折减比r=kφ/kc。
(4)当对粘聚力c 和内摩擦角φ同时进行折减时,始终保持r=k1/k2直到重力坝滑动失稳,从而得到两个安全系数k1和k2。
2.2 结构失稳判据
目前判定结构失稳的判据主要有[2]计算不收敛判据、位移突变判据及塑性区贯通判据。经研究发现计算不收敛判据在某些情况下得到的结果可能会夸大结构的安全裕度,建议在有限元抗滑稳定分析中联合采用位移突变判据和塑性区贯通判据[3]。本文基于以上两种判据对重力坝在设计地震作用下的稳定性进行分析。
3 实例分析
3.1 工程概况及有限元模型
我国西南某重力坝4#非溢流坝段三维有限元计算模型见图1,非溢流坝段坝高117 m,坝顶宽20 m,坝底宽90.95 m,坝段厚22 m。坝基绝大部分为Ⅱ类岩体,地表浅层部分坝基为Ⅲ1 和Ⅲ2 类岩体,坝基下有一条从上游倾向下游的软弱夹层,为Ⅳ类岩体。坝基范围取1.5 倍坝高,整个模型共划分单元7888 个,节点10498 个。坝体和坝基分别采用线弹性和摩尔-库伦材料。

图1 坝体-地基三维有限元计算模型
计算中采用材料参数见表1。
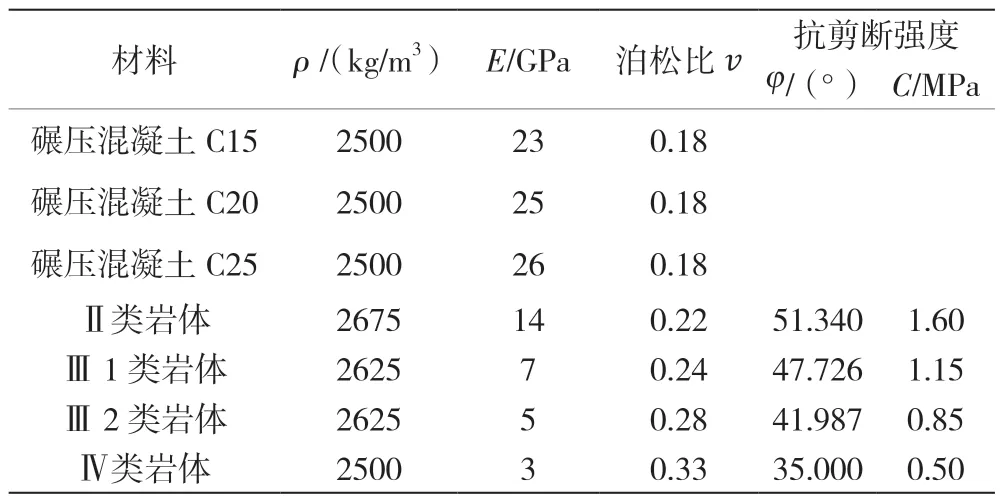
表1 材料参数表
上下游水头分别为113 m 和33.14 m,静力荷载包括坝体自重、上下游静水压力、坝基扬压力、淤沙压力等。动力荷载为动水压力及水平向峰值加速度为0.316g 的设计地震动荷载。根据地震安评报告提供的场地反应谱拟合成人工波,见图2,竖直向PGA 为水平PGA 的2/3,为0.211g。为了防止地震波在截断边界处发生反射,从而无法模拟地震波在地基中的真实传播过程,本文在截断边界处施加等效一致粘弹性边界[4]单元来模拟远域地基辐射阻尼的影响。
3.2 位移角度稳定性分析
依据2.1 节中叙述的双折减系数法计算过程,首先保持保持粘聚力不变,只折减内摩擦角直到重力坝滑动失稳得k=3.35;之后将坝基粘聚力和内摩擦角还原至天然状态下,保持内摩擦角不变,只折减粘聚力直到重力坝滑动失稳得kc=2.86,则折减比r=k/kc=3.35/2.86=1.17,按照折减比r=1.17对c 和 进行不同程度的折减直到重力坝滑动失稳。在地震的往复作用下,重力坝特征点位移也会随时间发生往复变化,仅以地震发生过程中某一时刻的位移随折减系数的发展情况不足以表征重力坝的稳定状态,应以震后残余位移随折减系数的发展情况来判定重力坝的稳定状态[5]。
在自然状态下,采用双折减系数法与等比例强度折减法计算的重力坝坝踵和坝趾位移特征点的位移值随折减系数的关系曲线见图3 和图4。以特征点位移发生突变为失稳判别准则,则基于双折减系数法得到的安全系数为2.2,基于等比例强度折减法得到的安全系数为2.25,两种方法得到的结果接近,双折减系数法得到的安全系数略小于等比例强度折减法,得到的重力坝失稳时的特征点位移值略大,说明等比例强度折减法夸大了重力坝的安全裕度。

图3 双折减系数法下特征点位移值与折减系数关系曲线图
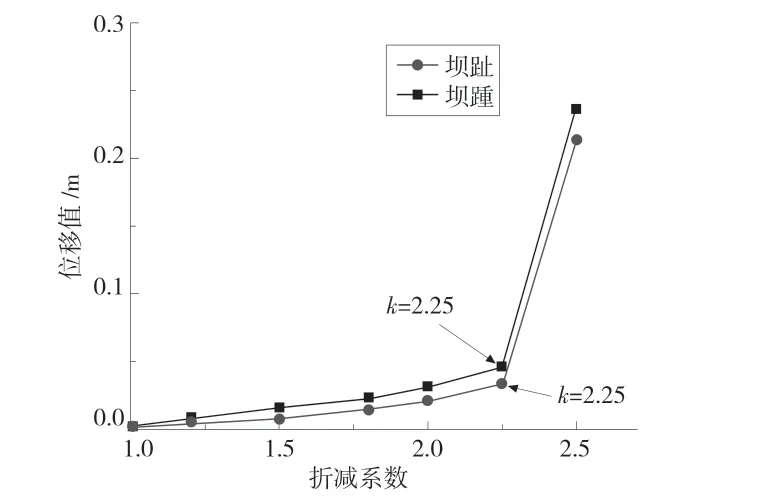
图4 等比例强度折减法下特征点位移值与折减系数关系曲线图
3.3 塑性区分布角度分析
以上从位移突变的角度对重力坝在设计地震作用下的稳定性进行了分析,为了佐证以上分析结论的正确性以及更为直观地看到坝基塑性区的发展状态。考虑到坝基岩土体的破坏过程是塑性区不断发展延伸直至结构失稳的过程,开始时坝基岩土体材料参数较强,只有部分单元处于塑性屈服状态,随着折减系数的不断增大,坝基岩土体材料不断软化,塑性区范围不断扩展,直至在坝基附近形成贯通的滑裂面时,即可判定重力坝滑动失稳。本文基于有限元软件的后处理功能输出重力坝坝基在不同折减系数下对应的塑性区分布云图,见图5。随着折减系数的增大,坝基岩土材料在不断软化,塑性区主要从坝踵及软弱夹层开始产生,之后塑性区由坝踵、坝趾两端向大坝中部发展,当折减系数k=2.2 时,重力坝坝基产生了贯通坝踵和坝趾的滑裂面,根据塑性区贯通判据可以判定,重力坝在此时发生滑动失稳。
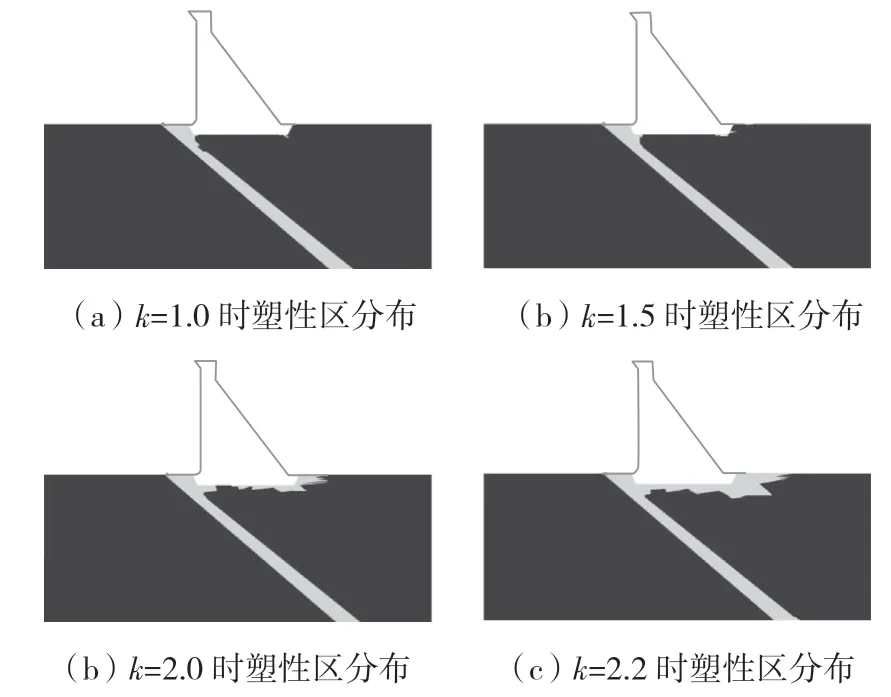
图5 设计地震时不同折减系数下的坝体损伤分布图
4 结论
(1)基于双折减系数法得到的重力坝抗滑安全系数略小于等比例强度折减法的结果,说明等比例强度折减法计算结果夸大了重力坝的抗滑安全裕度。
(2)采用双折减系数法分析重力坝在地震作用下的抗滑稳定性是可行的,且能更加真实地反映出重力坝在滑动破坏过程中粘聚力和内摩擦角各自的安全储备。
(3)在使用双折减法对重力坝抗滑稳定进行研究时,如何考虑坝基岩土材料抗拉强度的折减,有待进一步研究。

