基于Lu 模型的土石坝温度场对坝体渗流场的响应分析

唐友山

（江西交通职业技术学院,江西 南昌 330013）

1 研究背景

土石坝是多孔介质材料,坝体热量通过地表气温以热传导的形式传入坝体内部,在地下水渗流影响下,温度场会发生改变,温度梯度也会引起水体流动,同时,温度的变化也会使得流体物理性质发生变化,坝体渗流场与温度场是相互影响的耦合关系,可以通过研究坝体温度场的变化情况来反馈坝体渗流场,从而达到监测大坝渗漏的目的[1]。关于两场耦合的研究很多,多数研究只考虑单向耦合关系,如模型中未能考虑流体物性随温度的变化,非饱和区域的导热系数的空间非均质性等[2]。土石坝温度场受气温影响,在表层温度向大坝内部传递时,需穿过非饱和区域才能传递到坝体内部,非饱和渗流会影响坝体温度场,如土中含水率对传热参数的影响[3-5]。因此,不能简单地将非饱和土体当作干燥土体或者完全饱和土体计算,需考虑土体含水率影响,本文通过引入Lu 模型来刻画导热系数与含水量之间的定量关系,模型中同时考虑水体的温变效应,使得模型计算结果更加接近实际工程。

2 描述非饱和介质导热系数的Lu 模型

Lu 模型考虑土体矿物成分及含水率影响,导热系数在完全饱和土（λsat）和干燥土（λdry）间插值[6],其表达式为：

λdry和λsat分别为：

式中：λs为土中固体颗粒导热系数,,q 为石英在固体颗粒中的含量,λq为石英导热系数,λ0为其他矿物质综合导热系数,其中,λq=7.7 W·m-1·℃-1,λ0=2.0 W·m-1·℃-1（q＞20%）,λ0=3.0 W·m-1·℃-1（q＜20%）。

对于常规土,插值系数Ke为：

式中：χ为参数,对于粘土、壤土、砂土分别取0.58、0.9、1.05。

3 饱和非饱和渗流场与温度场数学模型

3.1 温度场影响下的饱和-非饱和渗流场控制方程

非饱和土渗流计算中,土体渗透系数的影响因素很多,含水率是重要因素,通常采用土水特征曲线来表征土壤含水率与渗透系数间的关系,研究中一般通过建立经验模型来进行计算,在众多模型中,VG 模型[7-8]具有参数物理意义明确、精度高、适应性广的特点,因此,本文选择VG 模型进行计算,其表达式为：

式中：h（θ）为土壤基质吸力；k（θ）为非饱和土体渗透系数；ks为饱和土渗透系数；θ为含水率；θr和θs分别为土壤残余含水率和饱和含水率；α和n 为与土体类别有关的参数,。

VG 模型参数可通过实验获取,没有实验条件的情况下也可按照经验取定。非饱和土水力数据库UNSODA[9]中含有世界各地大量土壤水力参数,可以通过在该数据库中查取水力参数,通过数据拟合得到VG 模型参数。缺少数据的情况下也可按照经验取定。

考虑温度对渗透系数和温度梯度对渗流的影响,得到渗流区域Ω内任意一点p（x,y,z）的总水头方程满足下式：

式中：H 为总水头；hp为土壤基质吸力；k 为土壤渗透系数；μ为给水度；Qh渗流源汇项；,为土体容水度；θ为土体含水率；n 为土体孔隙率；SS为单位贮水率；Γ为边界；其他符号意义同上。

3.2 渗流场影响下温度场控制方程

土石坝坝体热量传递包括渗流传热和多孔介质热传导两部分,则单位时间内流入土体单元的热量为：

式中：λ为导热系数；q 为热流密度；cw为流体比热容；ρw为流体密度；t 为时间；v 为流体流速。

流入单元体的净热量应等于单元体所吸收的热量,若单元体内无热源,则温度区域Ω内任意一点p（x,y,z）的温度函数T 应满足下式：

式中：T0（x,y,z）初始时刻温度场；S1为已知温度边界；T1（x,y,z）为已知温度边界；q（x,y,z,t）为已知热流边界（q=0 为绝热边界）；S2为已知热流边界；n2为S2法向；n3为S3法向；β为表面放热系数；Ta为地面温度；Qh问温度场源汇项；其他符号同上。

4 考虑非饱和渗流的坝体温度场特征

4.1 几何模型

几何模型为一均质土石坝断面,坝体填筑材料为粉土；最大坝高16.2 m,坝顶宽5 m。上游坡比为1∶3,下游坝坡为1∶2.5。坝脚设堆石棱体排水,顶宽1.5 m,高3 m,排水体的材料为砾石。为了便于分析计算结果,模型中取了7 个观察点（1#～7#）,各观察点坐标见表2,计算模型见图1。

图1 均质土石坝几何模型

表2 观察点坐标

4.2 计算参数

坝体材料的热力学和物理力学参数见表3。非饱和渗流参数参考文献见表4[11]。

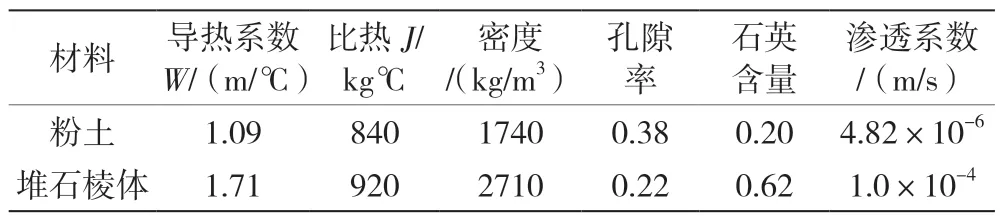
表3 试验土的热力学和物理力学参数

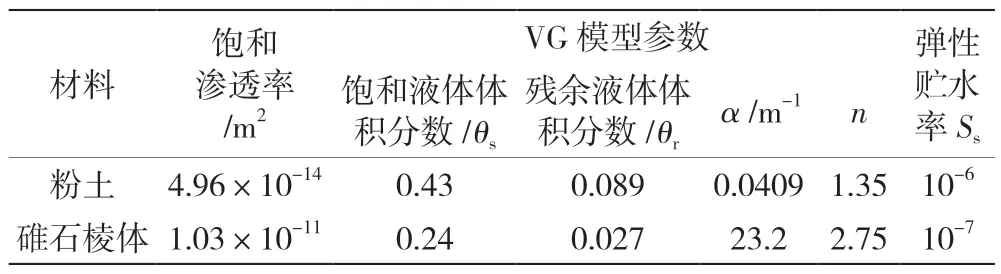
表4 非饱和渗流计算参数

4.3 边界条件与初始条件

渗流场边界设定为：上游边界AB 与下游边界DC 取为定水头边界条件,其他边界取为零通量边界条件。

温度场边界条件设定为：上游边界AB 与下游边界AD和DC 取为已知温度边界条件,坝底取为绝热边界。

4.4 计算模型

计算模型见图1,模型中采用Lu 模型来描述非饱和渗流区域土体的导热系数与饱和度的定量关系,由于comsol 软件自带的多孔介质热传导模块默认的导热系数为体积平均模型,需修改模块,引用Lu 模型。首先需定义λdry、λsat和λs,修改软件中热导系数方程。同时,模型中引入水的动力粘度和水密度与温度间的函数关系,待后续的模型参数定义时引用。

模型中其他参数的取值见表3 和表4。渗流场边界条件为：上游边界AB 水头为13.2 m,下游边界DC 水头为1 m,其余边界取为零通量边界；温度场边界条件为：上游坝面A 处温度设为18℃,上游坝面温度沿水深呈线性变化,库底温度稳定为5℃。下游边界AC 温度为20℃,BC 边界取为绝热边界,初始温度取为10℃。

4.5 计算结果分析

（1）液体体积分数对岩土体热参数的影响

图2 为大坝压力水头分布图,图中,压力水头为0 m 的等水头线即为坝体浸润线,非饱和区域土体饱和度会影响坝体材料的导热性。图3 为坝体非饱和区域的饱和度分布图。由图3 可知,作用在土体上的基质吸力使得地下水向上运移,浸润线附近及以下土体饱和度为 1.0,越靠近坝顶土体饱和度越低,坝体顶部附近的相对饱和度达到 0.5,棱体上边界的相对饱和度最低,为0.12,这是因为棱体材料为砾石,土体孔隙通道大,基质吸力低,水分向上迁移困难。饱和度在非饱和区域内非线性变化。

图2 压力水头分布图

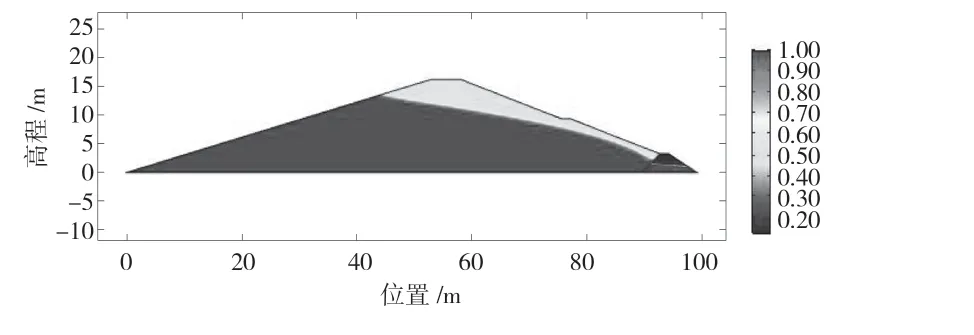
图3 相对饱和度分布图

非饱和带土体的导热系数与其含水量的关系是由 Lu 模型给出的,见图4,导热系数随液体体积分数的增大而增大。图5 为坝体非饱和土导热系数分布图。由图5 可知,浸润线以下的饱和土的导热系数为1.81 W·m-1·K-1,坝体导热系数最大值出现在下游水位以下的排水棱体处,为2.92 W·m-1·K-1,这是因为棱体材料为砾石,介质石英含量高,且水位以下岩体饱和,故导热系数最大。最小值出现在排水棱体上边界,为1.48 W·m-1·K-1,这是因为棱体上边界含水量最低,介质孔隙空气含量大,由于空气的导热系数远远低于水体导热系数,阻碍了热量在岩体中的传递,故导热系数最小。最小值为最大值的50.7%。

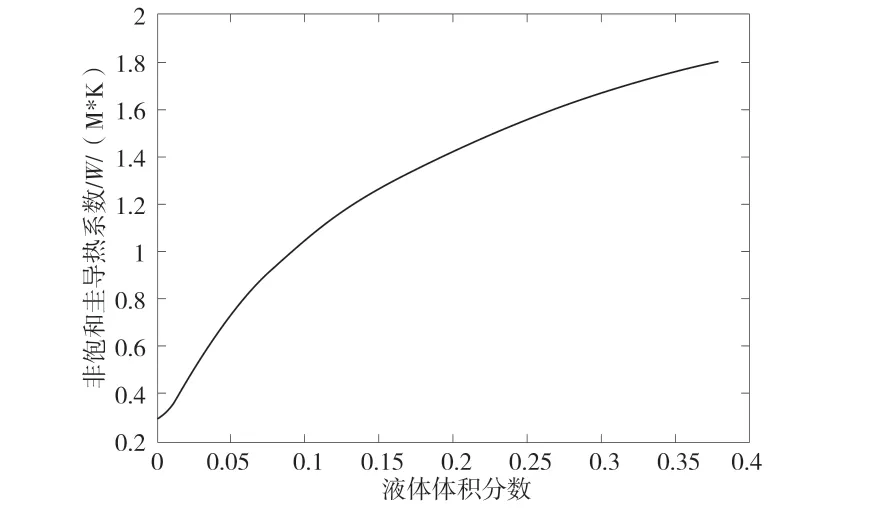
图4 非饱和土导热系数与液体体积分数关系图

图5 非饱和土导热系数分布图

（2）不同热参数计算方法的对比分析

在进行多孔介质渗流传热的数值模拟研究中,非饱和岩土体的导热系数取值,常用以下两种方法：（1）常量法,导热系数取值按饱和岩土体或某一含水量状态给出；（2）变量法,导热系数按固、液、气三相的体积分数确定。本文所采用的Lu 模型采用变量法,是一个半经验半理论模型,通过在comsol 中修改等效热传导系数方程来进行计算。在前面计算的基础上,通过引用不同的热参数计算方法来说明Lu 模型的有效性,工况假设见表5。表中为水体导热系数,取为0.58 W·m-1·K-1,为空气导热系数,取为0.024 W·m-1·K-1,按照Lu 模型给出的公式计算,其余参数同上。

表5 不同热参数计算方法的对比分析工况

运用上述5 种方法分别计算得到的导热系数垂向分布见图6。由图6 可知,Lu 模型、指数模型和体积平均模型在坝体垂向上均受含水率的影响,导热系数随高程的增大而减小,越靠近坝顶,导热系数越低,当高程低于11 m 时,坝体导热系数基本稳定不变,这是因为越接近坝顶,坝体填土含水率越低,故导热系数也越低,当高程低于11 m 时,土体饱和导热系数稳定不变,由图4 也可以看出,土体导热系数随含水率的增大而增大。

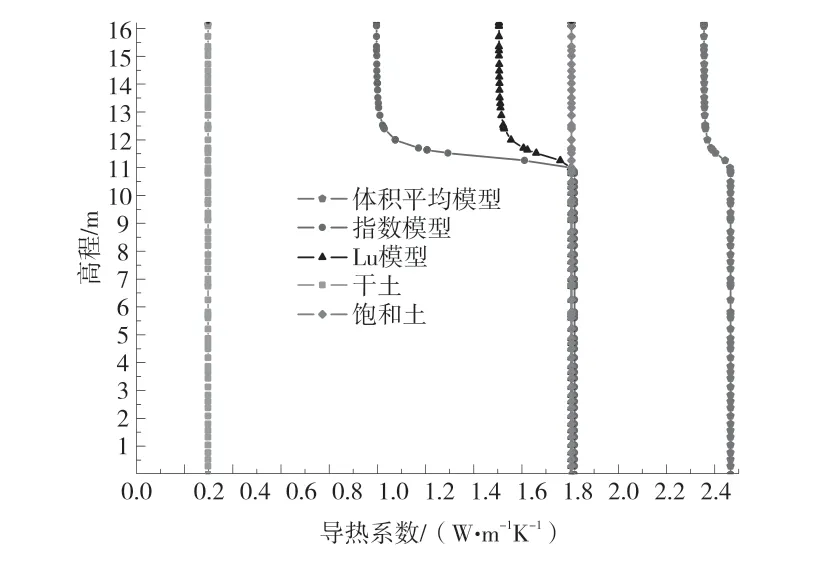
图6 不同热参数计算方法的非饱和土导热系数垂向分布

5 种方法分别计算得到的导热系数中,采用体积平均模型计算得到的导热系数最大,为2.35 W·m-1·K-1～2.46 W·m-1·K-1,超过了饱和土体的导热系数,同时变幅也最小,说明采用体积平均模型计算得到的土体导热系数与实际偏差较大；采用Lu 模型和指数模型计算所得到的导热系数分布形态相近,计算值很接近,均介于干燥土体导热系数值与饱和土体导热系数值之间,说明两种方法的计算值是合理的,且两种方法计算所得的导热系数受含水率影响很大,能够反应含水率与热传导系数的非线性关系。因此,采用Lu 模型可以很好地刻画导热系数与饱和度之间的定量关系,评价不同饱和度岩土体的导热系数,可为非饱和岩土体传热模型提供理论基础。

5 结论

（1）通过建立土石坝饱和-非饱和渗流场与温度场全耦合模型,可以为开展两场耦合数值模拟提供理论基础,从而建立更加精细的数值模型。

（2）Lu 模型能够精确的描述土体导热系数与含水率间的定量关系,相比于常用的体积平均模型,Lu 导热系数模型计算结果更加合理。