基于桥梁响应的高速铁路简支梁离心力折减方法

李奇 揭崇清 石龙 李克冰

1.同济大学 土木工程学院， 上海 200092； 2.中国铁道科学研究院集团有限公司 高速铁路轨道系统全国重点实验室， 北京 100081

为保证高速铁路行车安全性和乘坐舒适性，我国高速铁路大量采用以桥代路形式。简支梁因其构造简单、施工便利等优点，被广泛应用于高速铁路建设中。布置于铁路曲线段的简支梁受列车离心力作用，离心力是桥梁下部结构横向刚度设计的控制荷载。随着高速铁路速度标准的提高，铁路桥梁结构设计对梁体、墩台变形参数提出更高的要求，以满足线路平顺性的需求［1］。因此，研究高速铁路简支梁离心力对下部结构的设计具有重要意义。

TB 10002—2017《铁路桥涵设计规范》［2］规定在曲线上的桥梁，应考虑列车竖向静活载产生的离心力，其值为离心力率乘以竖向静活载。考虑到列车荷载图式远大于高速运行列车的实际轴重，针对列车速度大于120 km/h 的情况，引入列车竖向活载折减系数对离心力进行折减。刘普等［3］探讨了列车竖向活载折减系数取值来源，英国BS5400规范、德国DS804规范、欧洲国际铁路联盟UIC规范均给出了计算离心力的折减系数公式。其中，UIC71活载与中国规范的中-活载相近。因此，中国规范主要采用UIC 规范中的折减系数公式。然而，这一公式的理论来源鲜有严谨的论证报道，是否适配中国高速铁路ZK 荷载也缺乏足够的研究成果。

为了得到折减系数，需要获得运营列车对桥梁产生的离心力或由离心力引发的响应。一些国内外学者建立了列车-曲线桥梁耦合系统，并进行了桥梁振动响应分析。Xia 等［4］建立了列车-梁-墩耦合系统的动力学模型，考虑曲线段离心力作用，计算了桥墩墩顶横向振幅。Shi 等［5］建立了高速列车曲线通过简支梁的三维动力学模型，考虑轮轨间非线性蠕滑，分析了梁体的横向和扭转响应。宋郁民等［6-8］对列车通过曲线桥梁的车桥耦合振动进行了一系列研究，探讨了曲线桥梁响应振动规律。周海洋等［9］分析了铁路曲线上单跨双线简支梁的车桥耦合振动特性，对比了曲线与直线简支梁的响应差异。已有研究对曲线段车桥耦合振动仿真分析较多且相对成熟，但关于离心力和离心力折减系数的研究非常少见。

本文提出基于桥梁响应的高速铁路简支梁离心力折减系数的分析方法，采用车桥耦合振动仿真方法和反向传播神经网络，研究折减系数的影响因素，并评价TB 10002—2017中竖向荷载折减系数公式的适应性，为高速铁路桥梁离心力折减系数设计提供参考。

1 离心力及离心力折减分析方法

TB 10002—2017 中曲线上桥梁所受列车离心力（F）计算式为

式中：V为设计车速；f为竖向活载折减系数；W为列车荷载图式中的集中荷载或分布荷载；R为曲线半径；L为桥上曲线部分荷载长度。

采用ZK 荷载计算时，当V≤120 km/h或L≤2.88 m时，f= 1；当V> 250 km/h时，按V= 250 km/h计算f值；当L> 150 m时，按L= 150 m计算f值。

虽然折减系数计算公式理论来源不详，但含义较为明确。由式（1）可知，除了折减系数之外，离心力仅与速度、曲线半径和列车荷载图式相关。速度和曲线半径无法被折减，因此折减的实质是对列车荷载图式中竖向活载的折减。德国规范D804 中明确指出高速列车轴重比UIC 荷载图式小得多，为了计算与UIC荷载图式匹配的离心力，必须乘以一个折减系数。TB 10002—2017 吸纳了外国规范的相关规定，用于高速铁路的ZK 荷载为UIC 荷载的80%，但沿用了UIC 规范中的离心力折减系数公式。

列车的离心力是通过轮对和轨道作用于桥梁上，可视为横向作用于桥梁的移动荷载列。离心力会对桥梁产生周期性的动力作用，当加载频率与桥梁自振频率接近时会引起桥梁共振。虽然高速列车的轴重比货物列车小，但是其车速更高，因而产生的桥梁动力响应不容忽视。上述各国规范中均没有提及高速列车对离心力效应的不利影响，在离心力计算公式中没有明确体现这一动力特征。

借鉴动力放大系数计算理论，本文从桥梁响应的角度提出了竖向活载折减系数的计算方法，即

式中：SD为采用车桥耦合方法得到的桥梁动力响应；SW为按列车荷载图式计算的不折减的离心力产生的桥梁静力响应。

式（3）不仅直观反映了运营列车离心力对桥梁的作用效应与列车荷载图式离心力的作用效应之间的差异，还考虑了运营列车离心力的动力效应，延拓了离心力折减系数的内涵，对桥梁设计更具指导意义。此外，式（3）符合国际铁路联盟提出的列车荷载图式对桥梁的动力效应不应小于运营列车荷载对桥梁动力效应的理念。即运营列车荷载 × 运营动力系数 ≤ 列车荷载图式静力响应 × 设计动力系数。SD对应于运营列车荷载 × 运营动力系数，它考虑了移动荷载列作用和轨道不平顺对桥梁的影响；SW对应列车荷载图式静力响应；f对应于设计动力系数。

不同车型和桥型计算出的桥梁动力响应存在差异，根据相应的列车荷载图式效应可求得不同参数下的折减系数。因此，式（3）不仅可以计算合理的折减系数，还可以进一步分析其影响因素，对规范公式的适应性进行评估，进而为规范修订提供依据。

2 车桥耦合振动分析模型

2.1 车辆模型

为获得式（3）的折减系数仿真计算结果，选择8节编组高速列车为研究对象，主要参数见表1，计算速度为120 ～ 440 km/h。采用有限元软件ANSYS 建立车辆模型，导出其前31阶模态并基于模态叠加法进行车桥耦合振动计算［10］。为计算列车离心力对桥梁的横向响应，车辆建模时考虑车体和构架的横摆、侧滚、摇头、沉浮、点头自由度，以及轮对的横摆、侧滚、摇头、沉浮自由度。

表1 车辆模型参数

表 2 高速铁路曲线设计参数

2.2 桥梁模型

采用以直代曲的方式建立多跨简支梁桥的模型，并按平分中矢法布置墩位。桥梁参数参考高速铁路预应力混凝土双线简支箱梁桥的设计参数取值。

采用空间梁单元Beam188 模拟梁体和桥墩。梁体和桥墩的材料分别为C50 和C35 混凝土，桥梁建模长度约400 m，桥梁跨度取24、32、40 m，对应跨数分别为16、12、10。桥梁墩高为10 ～ 40 m。

将桥面上二期荷载作为主梁质量的一部分进行简化考虑，忽略桥上无砟轨道和桥梁之间的高频相对位移，假定轨桥变形主要由扣件弹性变形引起，将扣件弹簧与轮轨接触弹簧进行串联建模。简支梁的计算频率为1～7 Hz。

2.3 列车曲线通过处理

在整体坐标系下建立桥梁模型，所得振型向量及所得物理坐标下的振动响应也在整体坐标系之下，但轮对轴线方向不断变化，每个轮对都处于不同的移动坐标系下，需不断通过坐标变换建立轮对与桥梁的耦合关系。轮对-轨道-桥梁空间耦合关系见图1。

图1 轮对-轨道-桥梁空间耦合关系

坐标转换矩阵为

式中：α为曲线上任意点切线与水平轴的夹角，与曲线里程和半径相关；γ为超高角。

坐标转换后得到的振型向量是相对桥梁形心而言的，还需通过刚臂约束方程换算为相对轨道中心线处的振型向量。

为实现对列车通过完整曲线路段的模拟，采用由直线段、缓和曲线段、圆曲线段构成的曲线线路尺寸。曲线线路中超高、曲线半径和高速铁路设计速度等参数应相互匹配，根据TB 10621－2014《高速铁路设计规范》［11］和工程经验可得到曲线线路参数的常用匹配关系，见表2。

2.4 车桥耦合振动求解方法

假定车桥振动系统中不含Maxwell 阻尼，则车桥系统运动微分方程［10］可表达为

式中：qv、q̇v、q̈v分别为车辆模型的模态坐标向量速度、加速度；ξv为车辆模型的模态阻尼比矩阵；ωv为车辆模态圆频率矩阵；fv为车辆承受的外力及虚拟内力向量；下标b代表桥梁。

车辆和桥梁子系统运动微分方程的左端由模态频率、振型和阻尼比决定。由于非线性内力移项至方程右端，故方程右端力与车辆和桥梁响应有关。

桥梁结构的动力响应峰值主要取决于阻尼比。偏于安全设计，参考欧洲规范对预应力混凝土简支箱梁采用阻尼比的最低限值（1%）进行动力仿真分析，即各阶模态阻尼比均取0.01。轨道不平顺采用德国高速低干扰谱，数值计算方法采用4阶龙格库塔法求解，积分间隔为0.001 s。

3 桥梁动力响应

为探究在折减系数中考虑动力效应的必要性，采用车桥耦合仿真方法分析列车车速、曲线半径、桥梁墩高和跨度对桥梁动力响应的影响规律。

3.1 列车车速

由于列车轴重的规则性排列，列车对桥梁产生周期性的动力作用，当加载频率与桥梁自振频率接近时易引发车桥共振。列车通过简支梁的临界共振车速（Vres)［12-13］为

式中：fbn为桥梁第n阶自振频率；dv为整车长度；i为正整数，i= 1，2，3，…。

本文以32 m 跨度、20 m 墩高的12 跨简支梁为例进行分析，其第一阶竖向自振频率为4.69 Hz，由此得到竖向临界共振车速为417 km/h。

不同车速下梁体跨中竖向振幅见图2。可知，在车速420 km/h 时出现了明显的波峰，即在共振车速附近，跨中竖向振幅明显增大。另外，直线和曲线段桥梁跨中竖向振幅基本一致，表明桥梁竖向响应受离心力影响甚微。

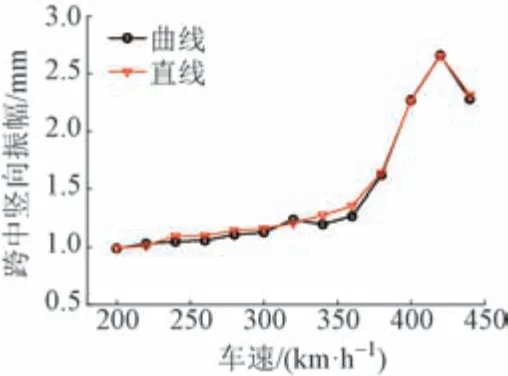
图2 不同车速下跨中竖向振幅

由于梁墩耦合作用，桥梁横向的振动特性较为复杂。列车运行在曲线外侧时，不同车速下墩顶横向振幅见图3。可知，曲线段桥墩墩顶横向振幅随着车速的增加而波动增长，在车速为300 ～ 350 km/h 时横向振幅显著增大，说明在离心力作用下，墩顶横向振幅具有明显的动力特征。另外，对比直线段和曲线段墩顶横向振幅可知，横向响应受离心力影响显著。

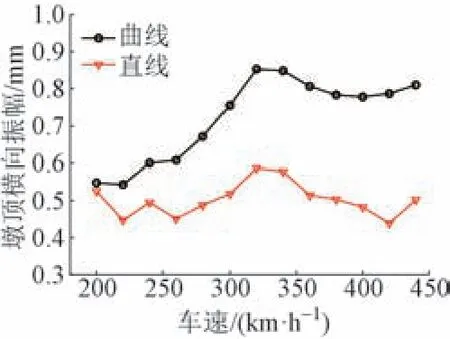
图3 不同车速下墩顶横向振幅

3.2 曲线半径

轨道超高分别考虑一致超高和平衡超高两种情况。一致超高是根据表2 中的取值来确定的，平衡超高是指满足车辆通过曲线所需的向心力平衡的超高。车速为250 km/h 时不同半径下墩顶横向振幅见图4。可知：①列车行驶于曲线外侧轨道时，离心力与列车偏载产生的桥墩横向位移同向，墩顶横向振幅随着半径的增大而减小；行驶于曲线内侧时墩顶横向振幅随着半径的增大而增大。②一致超高和平衡超高的计算结果基本一致。主要原因是超高的变化不会引起车辆作用于桥梁上的横向合力改变。

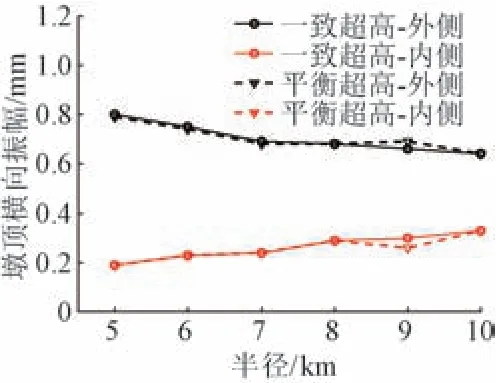
图4 不同半径下墩顶横向振幅

3.3 桥梁墩高和跨度

车速为250 km/h 时不同墩高和跨度下墩顶横向振幅见图5。可知，墩顶横向振幅随着桥梁跨度和墩高的增加而增大，且墩顶横向振幅对墩高的敏感性比桥跨更显著。

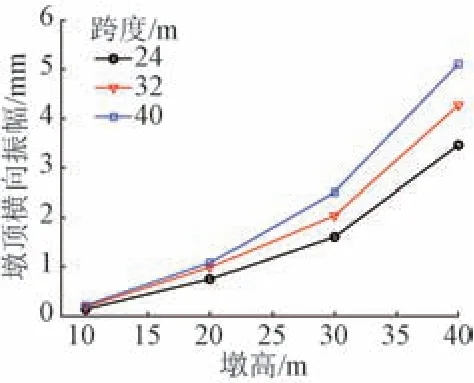
图5 不同墩高和跨度下墩顶横向振幅

综上，采用车桥耦合振动仿真方法可以得到不同跨度、墩高、曲线半径和车速下墩顶横向振幅，再现运营列车作用下桥梁结构在列车曲线通过离心力作用下的动力响应。计算结果表明，墩顶横向振幅受列车离心力影响显著，在特定车速下具有较明显的共振效应，体现了采用式（3）考虑桥梁动力效应计算竖向活载折减系数的必要性。

4 竖向活载折减系数

4.1 神经网络模型

为进一步分析列车竖向活载折减系数变化规律和影响因素，建立不同列车车速、桥梁墩高、跨度和曲线半径参数下折减系数的数据库，采用反向传播神经网络［14］建立多输入的相关模型。反向传播神经网络模型（图6）包括输入层、隐含层与输出层，这些层基本模块为神经元。神经元作为神经网络的基本单元，其作用是接收输入信号或前一层神经元的信号，经过处理后将信号中继到下一层神经元或输出结果。

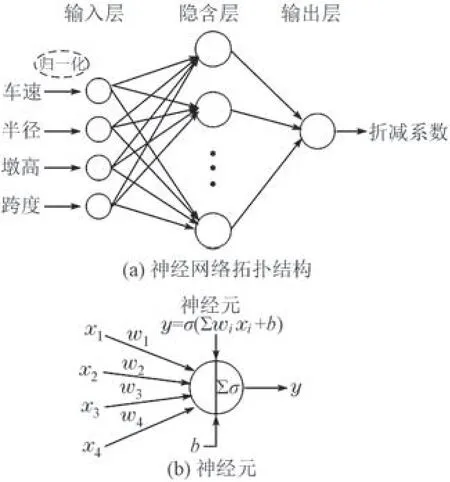
图6 反向传播神经网络模型

反向传播神经网络的训练过程分为正向传播和反向传播两个阶段。在正向传播阶段，输入数据通过神经网络各层的传递得到模型预测值。在反向传播阶段，采用损失函数计算预测值与真实值的误差，通过梯度下降等优化算法最小化损失函数，不断迭代调整神经网络的参数直至收敛。

反向传播神经网络具有良好的非线性映射能力，能够建立多变量映射关系，进而对竖向活载折减系数预测。在对神经网络训练前需要进行数据的归一化处理，目的是消除输入向量、输出向量之间的量纲影响。将建立的数据库按照3∶1的比例随机分为训练集和测试集，训练集用于训练神经网络，测试集用于测试神经网络训练的可靠性。为了避免过拟合问题的发生，在不断迭代和大量测试基础上，确定神经网络隐含层的神经元个数为6个，传输函数采用Sigmoid 逻辑函数。为了对该预测模型进行评估，需计算决定系数（R2）和均方根误差（XRMSE），其计算式分别为

式中：yi为原始数据；ŷi为预测数据；yˉi为原始数据的均值；m为数据库所有数据样本数。

R2越接近于1，说明该神经网络模型的拟合效果越好，但不能绝对确保预测值的准确性，所以还需结合XRMSE评估神经网络模型的预测精度。XRMSE表示预测值与真实值之间的平均偏差程度，其值越接近0，表示模型预测越准确。

对折减系数真实值与神经网络模型预测值的统计结果见图7。可知，R2和XRMSE分别为0.872和0.0429，说明该模型对折减系数具有一定的预测能力。

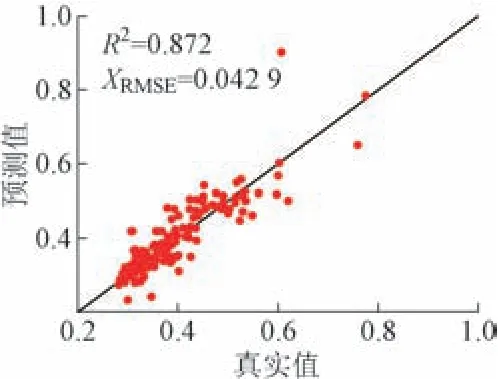
图7 真实值与预测值统计结果

4.2 影响因素的权重分析

网络的权重可以反映神经元输入信号对输出信号贡献的大小。为了探究4个输入变量对竖向活载折减系数的影响程度，计算输入层中各神经元对输出层中神经元的权重贡献度（Wik），表达式［14］为

式中：wij为输入层与隐含层之间的网络权重；wjk为输出层与隐含层之间的网络权重；r、s和p分别为输入层、隐含层和输出层的神经元个数。

根据式（9）计算的各变量对折减系数的权重贡献度见图8。可知，权重贡献度从大到小依次为车速、跨度、半径和墩高，车速权重达60%。其中，车速和跨度为影响较大的两个因素，这与TB 10002—2017 中竖向活载折减系数公式采用的两个自变量一致，验证了该计算公式在变量选取上的合理性。

图8 各变量对折减系数的权重贡献度

4.3 折减系数公式对比分析

规范竖向活载折减系数式（2）兼顾了客货共线铁路和高速铁路不同列车车型和车速状况，但是没有体现250 km/h 以上车速条件的影响。本文虽然只考虑了特定高速动车组的影响，但是如果认为车桥耦合振动仿真分析能在较大程度上反映实际运营情况，则根据式（3）计算速度350 km/h 以下高速铁路相应折减系数应小于式（2）计算结果才能保证依据现行规范设计桥梁的安全性。同时，式（2）能否适用更高速条件还有待商榷。为此，对式（2）折减系数计算结果与TB 10002—2017规范取值进行对比，见图9。

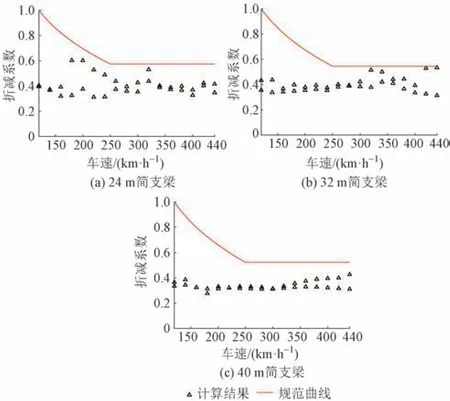
图9 折减系数计算结果与规范取值比较

由图9 可知：①规范取值能完全包络24、32、40 m跨度简支梁的折减系数计算结果，当车速小于250 km/h时，规范折减系数远大于本文计算结果，这是规范考虑的货物列车比高速列车轴重及相应离心力更大的缘故。②当车速为250 ～ 400 km/h 时，按本文方法得到24、32、40 m 跨度简支梁的折减系数最大值分别为0.530、0.533、0.426，而按规范计算的折减系数规范值分别为0.574、0.544、0.523，后者比前者分别大8%、2%、20%。这说明式（2）能够匹配高速铁路ZK 荷载及中国标准动车组，对速度400 km/h 内高速铁路常用跨度双线简支箱梁具有良好的适用性，具有合理的安全储备。此外，虽然UIC规范和TB 10002—2017规范中竖向活载折减系数来源不明，但能包络常用跨度和墩高简支梁及高速行车条件下的桥梁运营动力效应。

5 结论

1）列车车速对离心力计算时竖向活载折减系数的影响最大，其次为桥梁跨度，曲线半径和桥梁墩高的影响较小。

2）TB 10002—2017《铁路桥涵设计规范》中竖向活载折减系数公式反映了列车荷载图式与运营列车轴重的差异，折减系数应与列车荷载图式及实际运营列车荷载和车速相匹配。

3）TB 10002—2017 中竖向活载折减系数公式对中国高速铁路ZK 荷载及常用的高速动车组列车具有良好的适配性，能满足速度400 km/h 内高速铁路简支梁离心力设计要求。