跨被试运动想象脑电信号的卷积神经网络识别方法

魏明桦

（福州职业技术学院信息工程系，福建福州 350108）

0 引言

运动想象（Motor imagery，MI）是基于脑电图（EEG）的脑接机口（Brain-computer interface，BCI）中的关键技术之一，旨在通过被试者自主运动想象过程编码指令，并通过机器学习和模式识别方法解码指令，达到绕过肌肉系统从而直接控制外部设备［1］.人类在自主运动想象过程中（如：想象左手、右手、双脚或舌头），将会造成大脑对侧的电信号节律能量降低，同侧电信号节律的能量升高现象，即为事件相关去同步/同步现象（ERD/ERS）［2］.由于不同的MI任务可以产生不同的ERD/ERS 现象，因此对记录在MI-EEG 中的ERD/ERS 进行分类，即可解码出被试者的不同运动想象任务，从而进行辅助康复或脑感游戏等应用场景.因此，构建MI-BCI 的关键在于对EEG信号的分类与识别［3］.

针对MI-EEG 样本的识别算法主要包含两个分支，经典的方法基于信号处理方法，将EEG看作是多维时间序列，通过空域滤波器提取其中的空域特征，并直接使用分类器完成对空域特征的分类.经典的空域滤波器为共同空间模式（Common spatial pattern，CSP）特征［4］.该特征以二分类为目标，通过最优变换保证两个MI 类别差异最大化，将提取到的CSP 特征输入至线性判别分析（Linear discriminant analysis，LDA）模型中进行分类，从而完成MI-BCI 的识别过程.在此基础上，出现了一系列基于CSP 的特征提取方法，包括滤波器组CSP 特征（FBCSP），在空域滤波的同时保证不同频段［5］；约束CSP 特征（RCSP），在空域滤波的同时添加正则项，约束最优变换过程中的复杂性，提升空域特征性能［6］；复杂CSP特征（CCSP），在空域滤波时考虑时域、频域多种特征，构建出高性能、高鲁棒性的组合特征［7］.

经典空滤波特征提取受限于分类器的瓶颈，近年来，随着深度神经网络的发展，另一个MI-EEG 样本识别的分支为卷积神经网络（Convolutional neural network，CNN）.卷积神经网络在计算机视觉、自然语言处理中取得了显著的成就.文献［8］最早将CNN 应用至MI-EEG 的识别中，并证明了越简单的CNN 架构对EEG 的分类效果越好.通过所提出的ShallowNet 显著提升了，超越了经典的FBCSP 方法.在此基础上，研究者提出了诸多CNN 变种的算法，用于提升MI-BCI 的分类性能.主要包括：EEGNet 模型［9］首先进行滤波器组预处理后，再将不同频段的EEG 样本输入CNN 进行识别.MMCNN 模型［10］采用多分支结构提取不同时间尺度的MI-EEG特征，其性能比单一尺度的效果更好.

然而，EEG样本的获取成本较高，无论是经典的CSP特征提取方法，还是CNN模型方法，都无法应对MI-EEG的非线性、非平稳特性，导致被试间的样本无法一起使用.针对这个问题，一些研究者采用迁移学习的方法，从样本级或特征级进行跨被试迁移，从而提升被试间MI-EEG样本的泛化性，对抗不同被试者采集到的EEG 信号的非线性、非平稳特性.文献［11］最早将MI-EEG 样本投影至黎曼空间，并计算黎曼协方差矩阵均值（Riemannian alignment，RA），通过协方差矩阵的均值对齐不同样本，然后使用最短距离分类跨被试的MI-EEG样本.由于该方法对齐后的样本只有协方差特性，无法进一步提取有效特征，同时黎曼空间上的协方差矩阵的均值计算时间复杂度高.为了解决这些问题，文献［12］提出直接在欧式空间上计算协方差矩阵的均值（Euclidean Alignment，EA），从而提升跨被试MI-EEG 样本迁移的性能.在此基础上，文献［13］首先使用EA 方法对齐MI-EEG 样本，随后提取对齐后样本的CSP 特征，然后采用不同的域对齐方法进一步提升跨被试的MI-EEG识别性能.

实际上，现有的跨被试运动想象脑电识别方法，主要采用传统的样本或特征对齐方法，无法借助于深度神经网络高性能的特点，因此造就了实际MI-BCI 应用时的瓶颈.为了解决这个问题，本文提出一种全新的跨被试运动想象脑电信号的深度神经网络识别方法.该方法首先使用样本对齐方法，然后将对齐后的样本输入至卷积神经网络中，利用卷积神经网络的性能进一步提升MI-EEG样本识别效果，构建跨被试的MI-BCI应用.

1 跨被试运动想象脑电信号识别方法

1.1 基于协方差质心的跨被试样本对齐

在MI-EEG 信号跨被试者的迁移学习领域，目前主要存在三个层次的方法，包括样本级、特征级和模型级.在样本级迁移学习中，针对各个被试者的MI-EEG 样本，通过计算样本集的协方差矩阵来实现跨被试迁移.其中，协方差矩阵质心对齐算法（Covariance matrix centroid alignment，CMCA）是目前最为经典的无监督样本级迁移方法之一［12］.该方法的基本原理是通过使来自不同被试者的样本分布更加相似，从而在所有被试者的样本中训练出合适的分类模型.由于该方法具有无监督特性，因此可以将针对新被试者的样本集直接迁移至与训练集相似的分布，并使用已经训练好的模型来完成跨被试运动想象任务的识别.

假设来自被试者j的第i个MI-EEG 样本为sij∈RC*T，其中C为通道数，T为样本时域采样点.CMCA方法将EEG样本看作多维时间序列样本，首先通过下式计算其协方差矩阵均值：

其中，m表示第j个被试者的样本数量.Cˉj表示第j个被试者EEG样本协方差矩阵的算术平均值.平均值的计算可以有多种方式，一般可采用欧式距离、黎曼距离以及对数欧氏距离.我们将获得的矩阵称为协方差矩阵质心，并使用该矩阵对各个被试者的样本分布进行迁移对齐：

1.2 基于卷积神经网络模型的MI-EEG识别

经过上述的协方差矩阵对齐计算后，每个被试者样本的协方差矩阵都相同.由于协方差矩阵可以作为MI-EEG 样本的统计分布，因此可以在所有被试者的样本上构建卷积神经网络模型.为了提升CNN 模型的时频域特性，并降低模型的复杂度，使其能够应用至在线的MIBCI中，我们选择EEGNet模型［9］，该模型能够提取到时频域特性，保证所提取到的特征泛化性，而其又不会像如今复杂大模型那样，无法应用至实际的MI-BCI系统.

EEGNet 的网络结构如图1 所示.该网络包含三个卷积层，分别是时域、空域和分离卷积层，以及一个分类层.EEGNet 使用滤波器组将原始EEG 信号划分为不同的频带，同时进行三个卷积层的操作.如图所示，EEGNet 模型首先采用64*1 的1D 卷积核对时域采样点进行时域卷积操作，随后同样采用C*1的1D卷积核对所有通道进行空域卷积操作.接下来，针对各个特征图采用16*1 的1D 卷积核进行分离卷积操作，各个频带特征提取完成后进行连接；最终，所有频带的输出特征传递相连，采用SoftMax给出分类结果.

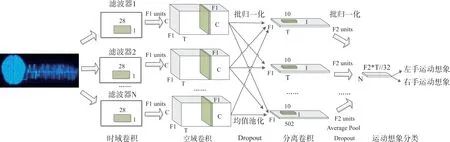
图1 EEGNet模型结构Fig.1 EEGNet model structure

针对EEGNet 模型，在训练过程中将对所有参数进行联合训练.在有监督的 EEG 信号模式识别过程中，EEGNet模型的训练就是找到一个高维映射函数，该函数能够提取输入 EEG 信号中特定类别的稳定特征，并将其映射到相应的类别.假设高维映射函数为f(xC*T；ξ) →yk，其中ξ表示待学习的网络参数，k表示可能存在的输出标签类别.在对MI-EEG 的识别中，通过深度神经网络对给定样本x提取运动想象的特征图，并采用SoftMax 函数给出特征图关于运动想象类别y的条件概率：

深度神经网络的训练目标是通过最小化所有训练样本的误差和，以确保测试样本集能够最大概率地获得正确的标签：

其中，损失函数采用对类别y的负对数似然损失（Negative log likely-hood loss，NLLLoss）：

可采用标签y的负对数似然估计形式：

1.3 EEGNet模型的训练设置

在跨被试的运动想象识别时，一般包含多被试者到单被试者的迁移方式，以及单被试者到单被试者的迁移方式.由于本文所构建的方法面向在线的MI-BCI 应用，我们选择多被试者到单被试者的迁移方式，该方式采用留一个被试者交叉验证的方式进行模型的训练和测试.具体地，每次选择一个被试者作为目标域被试者，将余下的所有被试者作为源域被试者.同时，将源域被试者所有样本进行训练，并在目标域被试者上进行测试.这样一来，针对m个被试者，一共进行m次训练和测试任务，并将m次测试的平均结果作为最终的识别准确率.

在EEGNet模型的训练时，采用Adam优化器，同时对于其中存在的卷积层和批量归一化层的参数采用均匀分布的方式初始化权重.按照常见关于MI-BCI 的CNN 模型训练设置，将每次训练的批次数量设置为64，将学习率设置为0.001，并构建了学习率衰减策略，训练轮数设置为200 次.当训练遭遇瓶颈时及时降低学习率，并重新调整训练和测试误差.同时，为了应对MIEEG 造成的过拟合现象，在训练过程中添加了dropout=0.5以及early stopping 策略.本文的硬件平台为：Intel i7-9700CPU，16 GB内存，以及RTX1080 GPU；软件平台为：Windows 10操作系统，加上的Python3.7搭配Tensorflow 2.1+Keras2.3.1的深度神经网络平台.

2 实验与结果分析

2.1 实验数据集

为了验证所提出方法的可行性与有效性，本文选择BCI Competition IV 2b数据集进行实验验证［14］.该数据集包括五个阶段，1-2阶段无视觉反馈，各包含120个带标签样本，阶段3有视觉反馈，包含160个带标签样本，4-5阶段无视觉反馈，各包含160个带标签样本.在本文的实验中，选择1-3阶段共计400个样本进行跨被试运动想象识别实验.在该数据集中一共包含9个被试者，我们采用留一被试交叉法完成实验验证.因此，每个跨被试MI-EEG识别实验中，一共包含400*8=3 200个训练样本，400个测试样本.在EEGNet模型训练时，按照8：2比例划分训练集和验证集.因此，训练集包含2 560个样本，验证集包含640个样本，测试集包含400个样本.

具体运动想象实验流程如下图2所示.每次实验（Trial）开始时，通过声音提示受试者做好准备.紧接着，屏幕会出现持续2 s的十字架，受试者需要注视十字架以集中注意力.随后，屏幕会随机出现提示运动想象的箭头，持续1.25 s.指示箭头出现1 s后，受试者开始运动想象，持续3 s.完成运动想象后，会给出大约1 s的随机休息时间，以便受试者调整状态并进入下一个实验（Trial）.

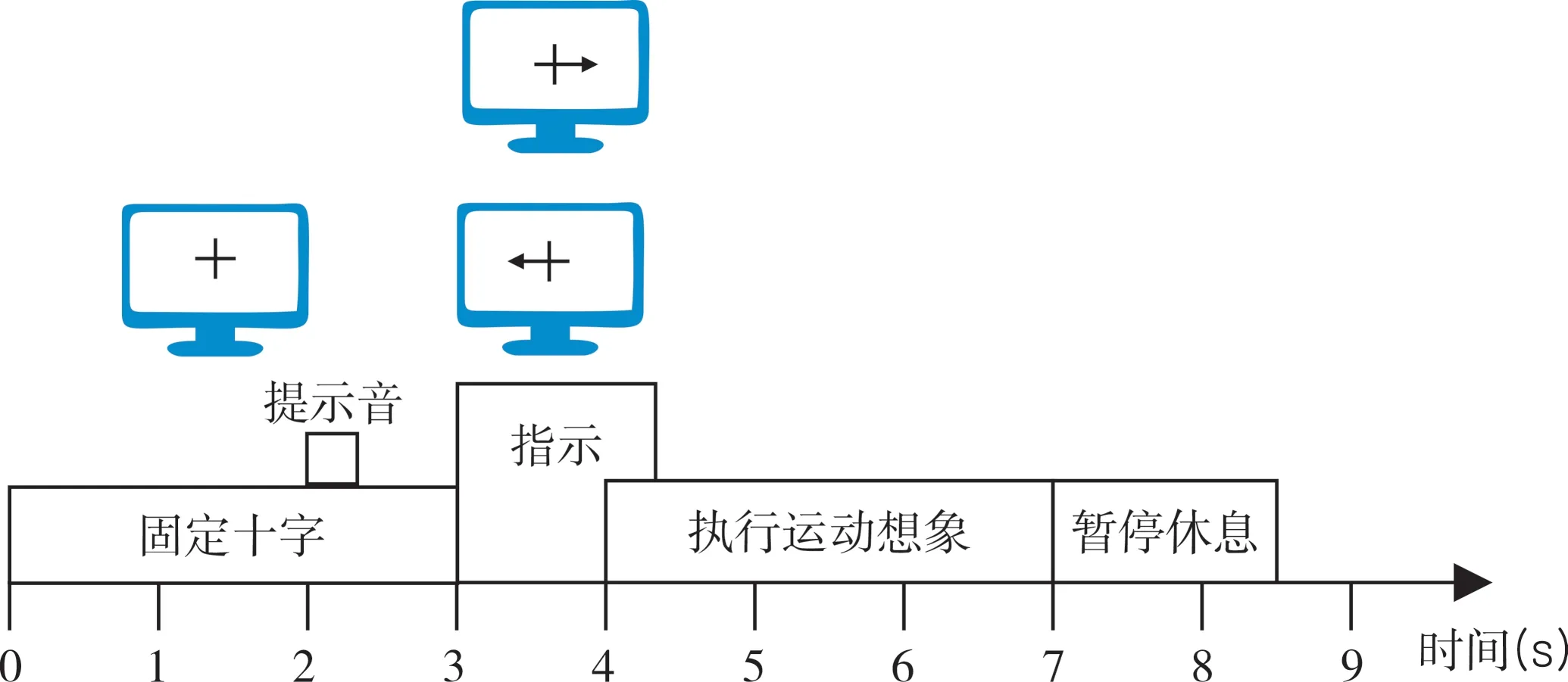
图2 BCI Competition IV 2b数据集的运动想象实验流程Fig.2 Experimental flow of motor imagery for the BCI Competition IV 2b dataset

2.2 对比方法

为了验证所提出方法的可行性与有效性，实验中选择近年来流行的跨被试运动想象脑电信号识别方法作为对比，具体如下：

（1）EA-CSP［12］：首先使用EA 方法对齐MI-EEG 样本，随后提取样本的CSP 特征，最后使用LDA 模型完成运动想象分类.

（2）RA-MDM［11］：首先将MI-EEG样本投影至黎曼空间，然后计算协方差均值并对齐每个样本，最后在协方差的形态下，计算最短距离作为样本分类依据.

（3）TS-CORAL［15］：这些方法首先使用EA 方法对齐MI-EEG 样本，随后提取样本的切空间特征，并使用相关对齐（Correlation alignment，CORAL）方法进一步对齐，随后使用LDA 模型完成运动想象分类.

（4）TS-JDA［16］：这些方法首先使用CMCA 方法对齐MI-EEG 样本，随后提取样本的切空间特征，并使用联合分布适应（Joint distribution adaptation，JDA）方法进一步对齐，随后使用LDA模型完成运动想象分类.

2.3 跨被试运动想象分类结果

表1给出了在BCI Competition IV 2b数据集上进行跨被试运动想象脑电信号分类的性能对比结果，其中采用协方差矩阵对数欧式均值进行对齐.从表1 中的结果可以看出，本文构建的方法取得了68.97%的平均准确率，高于所对比的四种方法.在测试过程中，本文采用留一被试交叉验证法，因此平均值表达出了最终的平均识别结果均高于对比方法，因此取得了更高的跨被试运动想象识别性能.

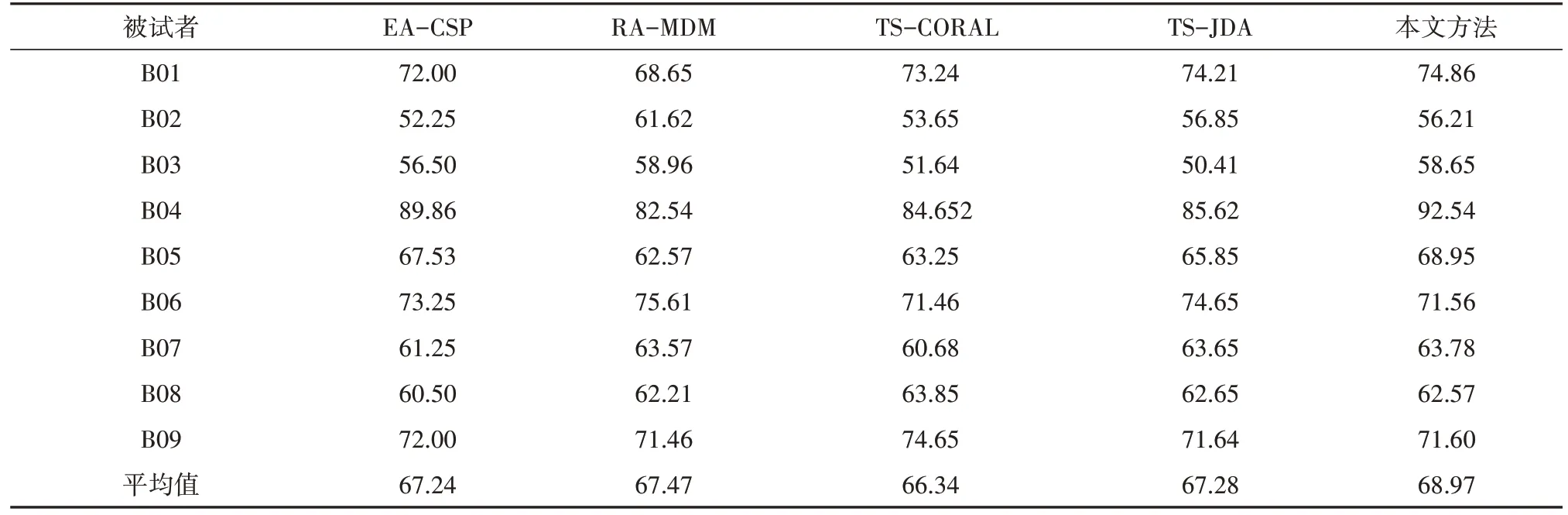
表1 跨被试者运动想象分类性能对比结果Tab.1 Comparison of classification performance across subjects

表2给出了在BCI Competition IV 2b数据集上进行跨被试运动想象脑电信号分类的效率对比结果.从表2中的结果可以看出，经典方法采用训练和测试的方式，因此没有验证时间消耗，而本文采用EEGNet 模型，在每轮训练过程中增加验证过程，因此包含训练时间复杂度和验证时间复杂度.相比于传统的非深度学习方法，EEGNet模型训练需要较多的迭代次数，因此需要更高的时间复杂度.然而，深度学习模型的优势在于仅需训练一次，即可在测试过程中多次使用.对比表2中的测试阶段可以发现，本文提出的方法与对比方法在测试时间上差别不大.因此，在实际使用时，本文所提出的方法并没有效率上的劣势，但是从表1 中可知该方法具有更高的识别性能.

表2 跨被试者运动想象分类效率对比结果Tab.2 The comparative results of the classification efficiency of motor imagery across subjects

2.4 消融实验

为了进一步进行本文所提出方法的分析，给出了两个消融实验，分别是不同协方差均值对齐的效果对比，以及迭代收敛情况，图3 给出了本文的消融实验结果.图3（a）给出了EA-CSP、RA-MDM 和本文方法在欧式均值、黎曼均值和对数欧式均值上的对比结果.从图中的结果可以看出，无论是在哪种均值下进行样本对齐时，本文所提出的方法均能够获得更高的性能，同时对数欧式均值对齐方式能够获得最高的跨被试运动想象识别性能.

图3 消融实验结果Fig.3.Results of the ablation experiment

在迭代收敛情况分析中，选择B04被试者作为目标域，余下的8个被试者作为源域，将对齐后的MI-EEG样本训练EEGNet模型.从图中的结果可知，经过有限轮数的迭代，训练误差和验证误差均获得了不同程度的降低，测试误差的降低趋势与训练误差和验证误差相同.同时，由于本文构建EEGNet 模型时采用了学习率调整策略，每次学习率调整时都需要回调误差，因此出现不同程度的波动.最终，通过early stopping策略停止了训练，获得了误差最低的最佳模型，用于跨被试运动想象识别的测试.

3 总结

针对运动想象脑电信号分类的性能瓶颈，本文结合协方差均值样本对齐方法与卷积神经网络模型，提出了一种新的方法.该方法能够通过协方差均值对齐降低不同被试者样本之间的分布差异性，提升MI-EEG 样本在被试间的泛化性.针对对齐后的样本，本文构建了能够提取时频特征的EEGNet模型，用于跨被试的运动想象分类，该模型吸收了卷积神经网络的优点.在BCI Competition IV dataset 2b数据集上的实验结果表明，本文所提出方法能的性能够超越现有经典方法，在跨被试运动想象脑电分类上取得了最高的性能，同时在测试场景中的时间复杂度与现有方法在相同数量级.今后的工作包含两部分，其一是寻找性能更高、更简洁的CNN模型，其二是将所提出的模型应用至在线的MI-BCI中，构建被试间可泛化的脑机接口应用.