源于宇宙弦的引力波暴及其电磁共振效应
王丽丽,史金磊,严建军,张 祎,杨 轲,赵 琳,杨静静
(郑州师范学院 物理与电子工程学院,河南 郑州 450044)
引力波是广义相对论的重要理论预言之一.2015 年9 月14 日,地面激光干涉引力波探测器LIGO(Laser Interferometer Gravitational Wave Observatory)首次探测到双黑洞并合产生的引力波[1].这直接证明了引力波和黑洞的存在,且在强场引力体系中与广义相对论符合得很好.幸运的是,之后又发现了更多的引力波事件,包括双黑洞、双中子星以及黑洞-中子星并合产生[2].这为观测天体和检验宇宙学模型提供了新的方法.
除了致密双星并合产生引力波外.加速运动的宇宙弦也是一个引力波源[3].它会向外辐射携带能量的引力波直至能量耗尽消失掉.在宇宙早期,高温相变产生的一维拓扑缺陷可以产生宇宙弦[4].宇宙暴涨可以产生宇宙超弦[5-8].宇宙(超)弦的演化进程对弦理论的研究至关重要.由于弦密度极大且引力极强.故而宇宙中只存在2 种形式的宇宙弦,即横贯宇宙的无限长长弦和大小不同的各种环形弦.宇宙弦形成之后会发生各种“重联”,要么弦自身的两端相互连接,要么与其它弦的两端相连,最终形成环弦或长弦.不同的弦重联概率不同.普通弦重联的可能性比较大,即为1.F 弦重组的概率为10-3≤p≤1,D 弦重组的概率为 0.1 ≤p≤1[6].弦 的这一进程被弦张力Gµ严重影响着.结果导致不同重组概率产生的弦网络特性和引力波的可探测性大不相同.这激起了物理学家研究宇宙弦和引力波的强烈兴趣.结合LIGO 和空间引力波探测器LISA(Laser Interferometer Space Antenna)的探测灵敏度,物理学家们给出了宇宙弦张力的各种限制.Damour 等认为普通弦Gµ~10-13辐射的引力波就具有可探测性[9-10].与普通弦不同,Jones 和Kachru等认为F 弦和D 弦1 0-11≤Gµ≤10-6才可以被探测到[8,11].Matsui 和Kuroyanagi 利用ALIGO(Advanced LIGO)和脉冲星计时阵PTA(Pulsar Timing Array)分别给出高频和甚低频引力辐射最新的限制,即Gµ≤10-5,Gµ~4×10-8[12].然而,长弦上逆流摆动产生的引力辐射在阻尼摆动方面的效率远不如最初想象的那么高[13].致使新形成弦环的特征长度与标准估计相差一个因子 ϵ ≡a/a0(ϵ ≪1)[14].考虑以上因素的影响,Damour 等[15]认为修改后的模型中Gµ~10-10时,ϵ ≥10-11(LIGO)和 ϵ ≥10-7(LISA)引力波暴可能被实现探测研究.
除甚低频、低频和高频引力波之外,宇宙弦模型也可以预言出甚高频引力波[16-17].近几年,甚高频波段的引力波被李芳昱教授等[18-25]提出的探测方案广泛讨论和研究.由于重组概率p和 ϵ两个参数直接和间接影响引力辐射的强度,从而影响引力波的探测需求.故我们利用此探测方案[26],结合引力波与电磁场的共振响应来讨论引力波暴的特性以及信号光子流和探测方案对此引力波的灵敏特性—信噪比.
本文的结构如下:第1 部分,介绍宇宙弦环震荡尖端产生引力辐射的模型.第2 部分,介绍微波频段引力波的电磁共振效应.第3 部分,主要从引力波幅值h、信号光子流和信噪比3 方面进行数值分析研究.第4 部分,给出本文的总结以及展望.
1 引力波暴辐射模型
宇宙弦环震荡引起尖端发生甚高频引力辐射.引力辐射所携带的能量与重组概率p和弦环长度参数 ϵ密切相关.在标 准模型中重组概率p=1,ϵ=1.与之不同,本文将考虑2 个可能影响引力波能量的因素:①宇宙弦重组概率低,即p≪1;②环弦长度特征参量 ϵ ≪1.那么修正后的宇宙弦理论模型以p和 ϵ为自由参数,可得引力波暴的量纲为1 的振幅为[15]:
式中:t0≃1017.5s 为目前宇宙的年龄;α0=ΓGµ为标准模型下量纲为1 的环长参数;G为万有引力常量;µ是弦张力;Gµ 是宇宙弦张力参数[27].y(p,ϵ)=10-2pϵ5/3N˙t0α08/3(νgt0)2/3/c0中c0为环在一个震荡周期内出现的尖端平均个数;νg是引力波的频率;N˙是引力波暴的事件发生率.按照宇宙的不同演化时期,g(y)=y-1/3(1+y)-13/33(1+y/yeq)3/11是1 个分段插值方程,描述的是振幅在3 个区域y≤1,1 ≤y≤yeq和y>yeq的幂率行为,其中yeq=zeq11/6,zeq≃103.94是物质与辐射密度相同时的红移;Θ是 以1 -θm为变量的Heaviside阶跃函数.(1+zm)1/6(1+zm/zeq)1/6,zm(y)=y1/3(1+y)7/33(1+y/yeq)-3/11表示模型中最大的红移.
2 引力波暴的电磁共振效应
宇宙弦环震荡产生的尖端辐射可以通过电磁共振方案来检测.这一过程主要分为2 步.①沿z轴传播的引力波穿过具有基频模式且沿z轴方向传播的高斯光束(微波频段)和沿y轴方向分布的均匀恒定静磁场时,将会引起时空的扰动从而激发扰动电磁场;②当引力波的频率与高斯束的频率相同时,扰动的电磁场与高斯束耦合作用产生可观测的物理效应,即扰动光子流[25].由于沿x轴方向的信号光子流强度大于其它方向[24],故本文只考虑沿x轴方向的横向光子流作为讨论对象.
需要注意的是,在信号探测中,热噪音、散粒噪音等噪音将会干扰信号的探测.信号和噪音的比值可以反映该探测方案的基本特性,故研究信噪比是非常有必要的.与热噪音和散粒噪音相比较,高斯束(背景电磁场)产生的背景光子流强度更大,因此被考虑为系统的主要噪音.在高斯束不变的情况下,信噪比越大表明引力波的强度越大,相对来说噪音对此类引力波信号的干扰越弱,越有可能被探测到.
背景光子流是由背景电场和背景磁场相互作用产生的.假设背景电场是以基频模式的高斯光束形式分布,则可以表示为:
引力波是背景时空的扰动.当引力波的频率与高斯束的频率相同时,沿z轴传播的引力波与静磁场共振作用产生横向扰动电磁波.考虑到引力弱场的性质,因此在计算过程中忽略二阶及高阶扰动,只考虑一阶扰动的影响.通过求解弯曲时空中麦克斯韦方程组,可获得一阶扰动电磁波分量为:
式中:上标“~”(“ ∧”)表示电磁场是时变场(恒定场);上标“(0)”(“(1)”)代表的是背景场(扰动场).背景均匀静磁场作为电磁谐振探测方案的重要组成部分,它的分布是沿着y轴正方向并且在z轴方向上的分布范围为:-l1≤z≤l2,l1=5.7 m,l2=0.3m.
利用真空中的坡印廷矢量S=E×B/µ0,结合式(3)与(4)和(4)与(5),单位时间内沿x轴方向的背景光子流密度和扰动光子流密度分别为:
式中:符号“ 〈〉” 表示在1/νe的 时间尺度求平均值;µ0是真空的磁导率;h¯ωe是一个光子的能量.由(6)式可知,不等于0,高斯束将会随着 |z|的增大而逐渐弥散开.分别对(6)式和(7)式积分,可以得到单位时间内沿x轴方向的背景光子流强度和扰动光子流强度分别为:
这里 Δs是yOz平面上典型的光子“接收面”.
3 数值分析
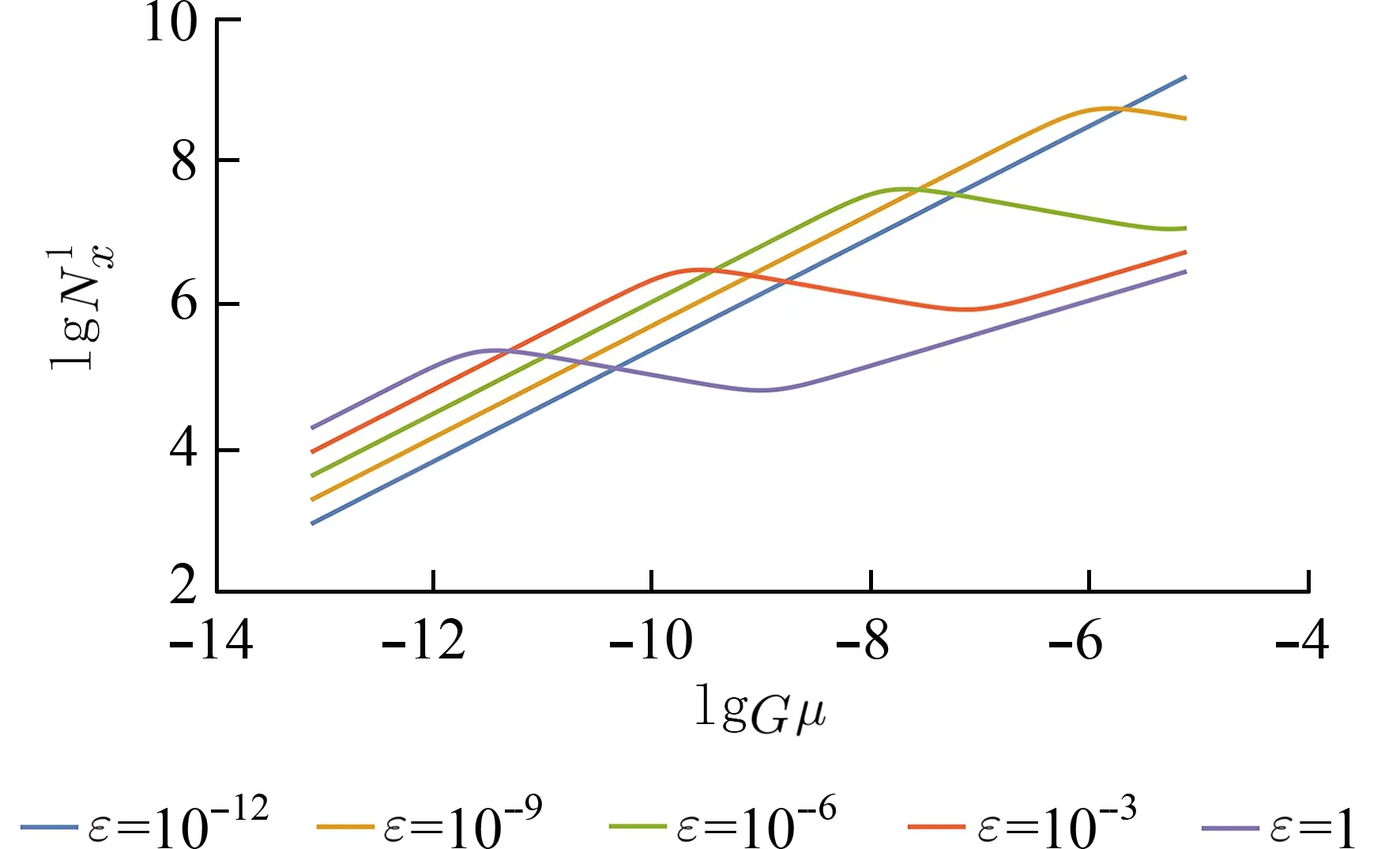
根据以上的引力波暴辐射理论介绍,我们进行以下的数值分析.为了保守估计,我们假定c0=1.其它参数的数值:N˙=1[15],Γ=50[28].为了结合引力波的电磁共振探测方案,在这里我们选取引力波暴的频率 νg=5×109Hz,(8)式和(9)式的积分区间:0 图1 重组概率p 对引力波暴振幅的影响Fig.1 The influence of reconnection probability p on the amplitude of gravitational wave burst 图2 参数 ϵ对引力波暴振幅的影响Fig.2 The influence of parameter ϵ on the amplitude of gravitational wave burst 然后,结合微波频段引力波的电磁共振作用,我们可以获得信号光子流的强度(如图3 和图4)以及在电磁共振探测方案中,信噪比的情况(如图5 和图6).从图3 和图4 可以看出,信号光子流强度随弦张力Gµ的变化趋势与引力波振幅强度一致.在相同的弦张力Gµ情况下,较小的重组概率p将会产生较强的可观测效应. 图3 重组概率p 对信号光子流的影响Fig.3 The influence of reconnection probability p on the signal photon flux 图4 参数 ϵ对信号光子流的影响Fig.4 The influence of parameter ϵ on the signal photon flux 图5 重组概率p 对信噪比S 的影响Fig.5 The influence of reconnection probability p on the ratio of signal to noise S 图6 参数 ϵ对信噪比S 的影响Fig.6 The influence of parameter ϵ on the ratio of signal to noise S 宇宙弦环震荡引发的尖端引力辐射强度比较弱.加上外部噪音的干扰,目前实验中还未探测到此类引力波.本文以重组概率p(10-3,10-2,10-1,1)和ϵ(10-12,10-9,10-6,10-3,1)为自由参数,弦张力Gµ(10-13≤Gµ≤10-5)为自变量,先对理论模型进行研究.主要体现在3 个方面:①保守估计引力波暴量纲为1 的振幅强度范围为10-28~10-25,p越小引力波强度越强,而 ϵ对引力波强度影响较小;②在微波 频段,信号光子 流强度达到 104~108s-1;③在微波频段,信噪比达到1 0-20~10-14.与遗迹引力波[22]和原初引力波相比[23],无论是引力波强度,还是电磁共振效应—信号光子流强度和信噪比,均要高出至少2 个数量级甚至更高.因此,宇宙弦模型预期的原初引力波在未来有很大可能性被探测到.这不仅对引力波本身有重要的科学意义,而且对极早期宇宙,尤其是宇宙大爆炸后瞬间的观测提供了可能.一旦未来探测到此类引力波,它将会对各种宇宙学模型的鉴别和判断提供关键证据.甚至可能对一些重大的基本科学问题,如时间的起点、时空的维度以及暗能量的本质等提供深刻的判断.




4 总结

