基于能量转化原理的地铁板式轨道自密实混凝土本构行为
陈俊豪, 曾晓辉, 谢友均, 龙广成, 唐 卓
(中南大学 土木工程学院,长沙 410075)
CRTS Ⅲ型板式无砟轨道是我国自主研发的新型轨道结构,以自密实混凝土(self-compacting concrete, SCC)作为充填层材料,替换了CRTS Ⅰ型和Ⅱ型轨道中的CA砂浆,使得施工更加便利。通过借鉴高速铁路的先进技术,地铁板式轨道也逐渐用SCC替换了原有CA砂浆或自流平砂浆,其结构主要由钢轨、扣件系统、轨道板、土工布、SCC填充层和支撑层组成,如图1所示。充填层在结构中主要起填充、承力以及减振等作用,对轨道结构的稳定性和耐久性等都有重要影响[1]。
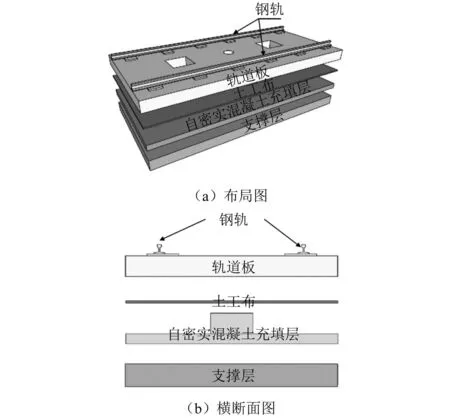
图1 地铁板式轨道结构图
在服役过程中,充填层结构主要承受竖向荷载,列车在行驶过程中对SCC充填层产生动态加载,且加载速率不断变化[2-3]。不管是CA砂浆还是SCC,均是1种典型的黏弹性材料,其力学性能具有明显的应变率特性[4]。国内外研究者对CA砂浆力学性能的应变率特性做了大量的研究[5-6],而关于地铁板式轨道SCC的研究还相对较少。龙广成等[7]利用霍普金森压杆研究了充填层SCC在10~100 s-1条件下力学性能的应变率敏感性,但10~100 s-1的应变率条件仅能满足地震或爆炸荷载产生的应变率范围,地铁实际工况中的应变率范围更小。此外,材料宏观力学性能的本质是能量变化,研究SCC在不同应变率条件下受压破坏过程的能量机制,可以了解SCC的能量转化规律,从而通过改变物相组分有效地改善和控制SCC的能量转化与释放规律,以满足地铁运营需求。然而,目前尚未见从能量转化角度研究应变率对地铁板式轨道SCC本构行为影响的成果。
充填层结构由于长期承受车辆荷载,极易产生劣化。目前,在机场跑道[8]、高速公路路面[9]、铁路轨枕[10]以及防撞护栏[11]等经常承受动荷载的结构中,通过在混凝土中加入废弃橡胶,使结构具有良好的韧性、抗裂性和抗冲击性[12]。为了推进橡胶自密实混凝土(rubber self-compacting concrete, RSCC)在地铁板式轨道中的工程应用,有必要对其在地铁服役条件下的本构行为进行系统研究。
1 试验概况
1.1 试验材料及试件制备
胶凝材料包括水泥(C)、粉煤灰(FA)和矿渣(SL),水泥为湖南东坪水泥有限公司生产的P.O 42.5普通硅酸盐水泥,粉煤灰为湖南湘潭电厂提供的Ⅰ级粉煤灰,矿渣为上海宝钢新材料公司提供的S95粒化高炉矿渣,胶凝材料的技术指标均符合相关规定[13-15]。胶凝材料的化学性质采用X射线荧光光谱法测定,比表面积采用Blaine法测定,其物理和化学性质如表1所示,粒径分布如图2(a)所示。

表1 胶凝材料化学组成和物理性能
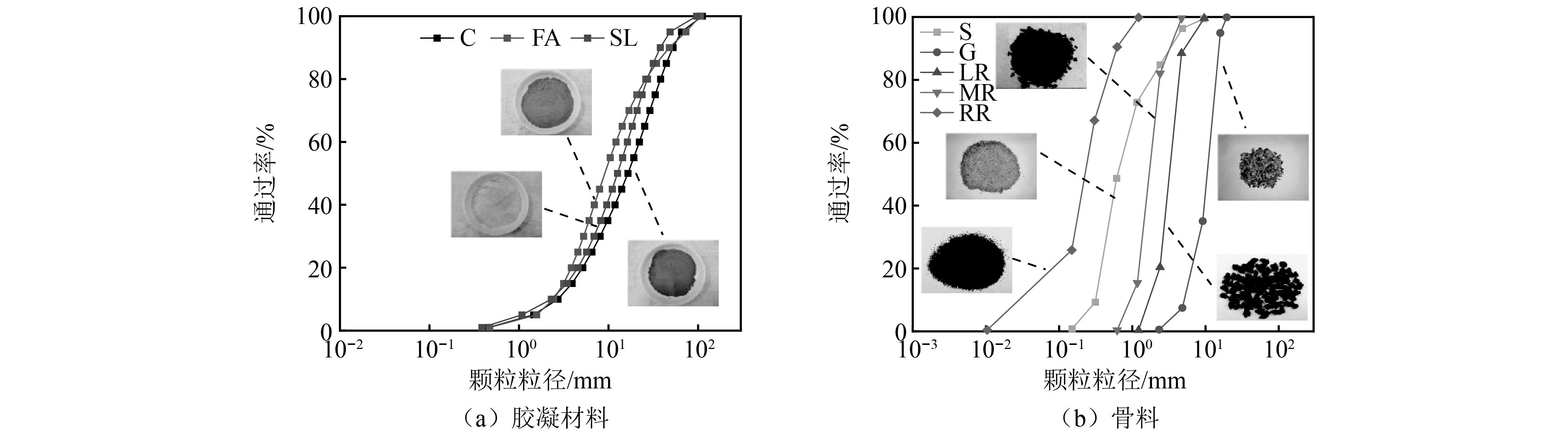
图2 粒径分布
细骨料为普通河沙(S),细度模数和比重分别为2.6和2.65,累积筛余百分数符合TB/T 3275—2018《铁路混凝土》[16]中Ⅱ区级配范围,粗骨料为石灰石碎石(G),由5~10 mm和10~16 mm两个级配按2 ∶3的比例混合而成,比重约为2.68,骨料的技术指标均符合相关规定。RSCC由橡胶颗粒等体积替换普通河砂组成,橡胶比重为1.0,抗拉强度为8.0 MPa,初始弹性模量为3.4 MPa,分为3种不同的尺寸,即2~4 mm(LR)、1~2 mm(MR)和0~0.3 mm(RR)。普通河砂、石灰石碎石和橡胶的粒径分布如图2(b)所示。
高效减水剂(SP)为聚羧酸类减水剂,减水率和含固量分别为26%和33%,由安徽中铁工程材料公司提供,拌合水(W)为饮用自来水,减水剂和拌合水的性能均符合相关规定。
试验配合比如表2所示,包括1组SCC和5组RSCC,其中S0为SCC,S1、S2和S3分别为MR橡胶掺量10%、20%和30%的RSCC,S4和S5则分别是LR和RR橡胶掺量30%的RSCC。
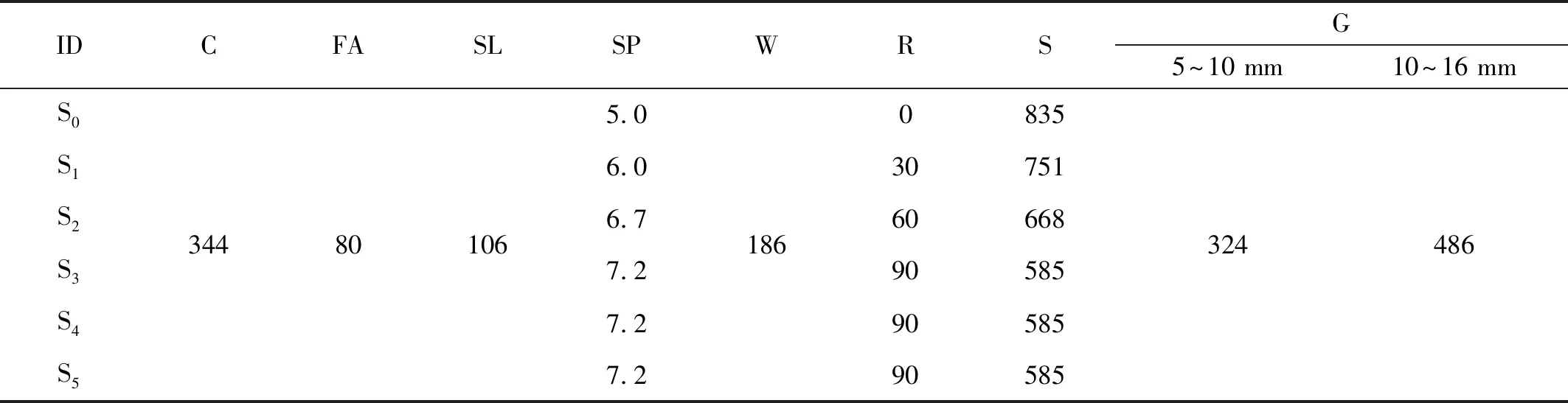
表2 试验配合比
混凝土搅拌完成后,立即进行工作性能测试,然后装入100 mm × 100 mm × 100 mm的试模中,1d后脱模,将试件放置在相对湿度大于90%、温度为20℃±2℃的标准养护室中养护至56d进行后续试验。坍落扩展度(slump flow)和扩展时间(T50)试验根据JGJ/T 283—2012《自密实应用技术规程》[17]和文献[18]的相关规定进行测试,力学性能试验按照GB-T 50081—2019《混凝土物理力学性能试验方法标准》[19]的相关规定进行测试。6组试件的工作性能和力学性能如表3所示。从表中可以看出,橡胶的加入会导致自密实混凝土的坍落扩展度降低,扩展时间和含气量增加,抗压强度降低,表明橡胶自密实混凝土的工作和力学性能降低。
1.2 试验方法
为了使单轴抗压试验中加载应变率符合地铁板式轨道的服役条件,根据相关研究,国内地铁最高设计时速为160 km/h[20],经计算车厢间车轮对轨道基础的作用频率约为7.04 Hz,地铁板式轨道充填层的最大动力荷载约为4 MPa[21],自密实混凝土充填层的弹性模量要求为3.0×104~ 3.8×104MPa。
综上,以弹性模量3.8×104MPa为例,计算得到自密实混凝土在荷载为4 MPa、作用频率为7.04Hz条件下的应变率为7.4×10-4s-1。在实际工程中,自密实混凝土的弹性模量要小于3.8×104MPa,列车的运行速度在0~160 km/h内变化,因此实际应变率会小于7.4×10-4s-1。通过上述计算,本文设定10-5s-1、10-4s-1、10-3s-1、10-2s-1共4种应变率进行试验,所选应变率范围符合地铁板式轨道的服役条件。为节约试验成本,仅对试件S0和S3进行4种应变率的单轴抗压试验,而S1、S2、S4和S5则只进行应变率为10-5s-1的试验,每组试件的试验个数为1个。
试验开始前,先将所有试件接触面打磨平整,保证上下接触面的高低误差在0.5 mm以内。试件被放置在加载平台中心位置,正式加载前,先对试件进行三次预压,以确保试件与加载平台紧密接触,然后根据设定的应变率进行试验。
2 试验结果分析
2.1 应力-应变曲线
2.1.1 不同橡胶掺量
不同橡胶掺量下,试件S0~S3的应力-应变曲线如图3所示,从图3中可以看出,随着橡胶掺量的增加,曲线形状由“高瘦”向“矮胖”变化,峰值应力后,曲线下坡段趋于平缓,SCC的韧性加强,脆性得到改善。
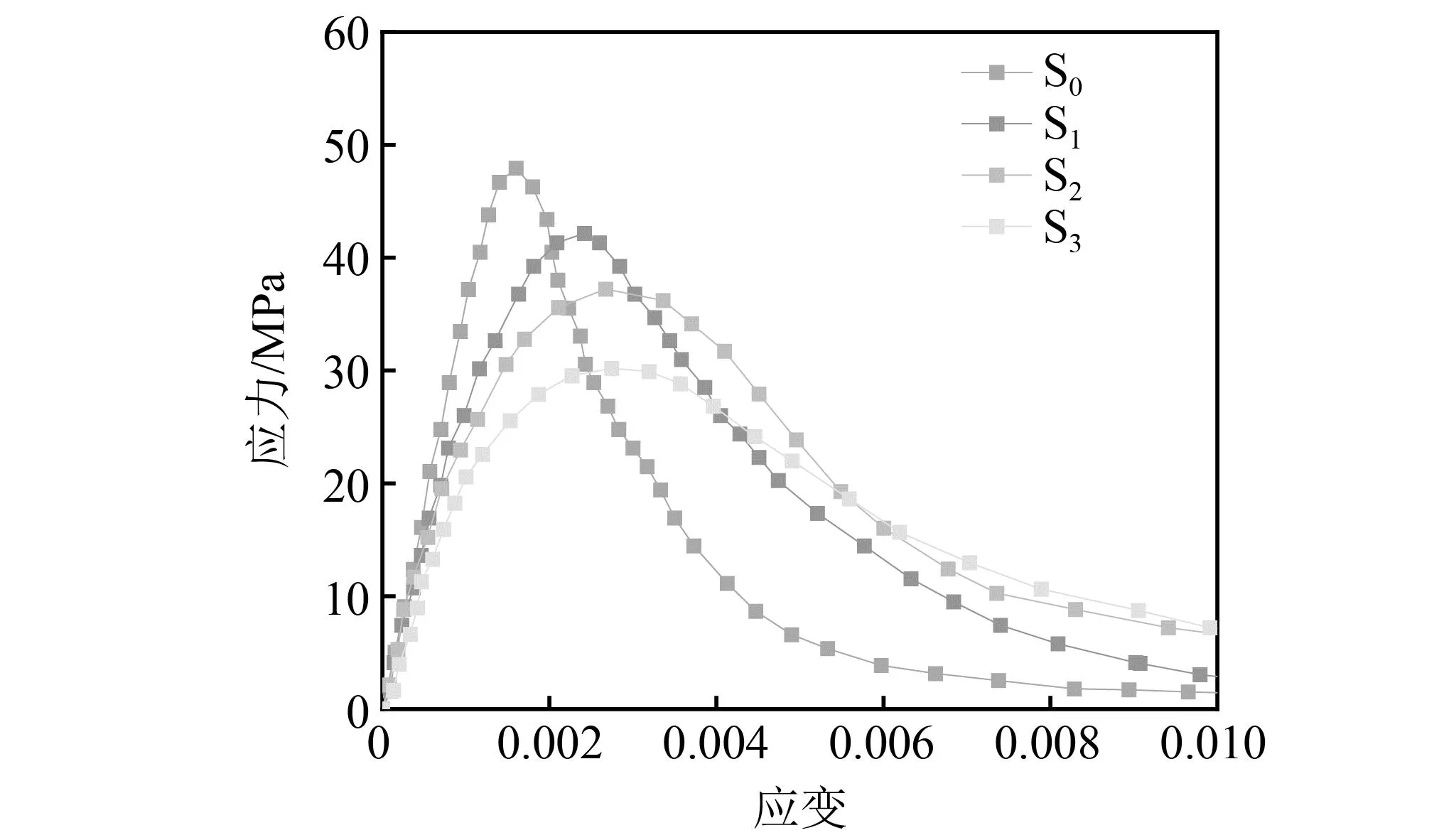
图3 不同橡胶掺量下试件S0~S3的应力-应变曲线
随着橡胶掺量的增加,试件S0~S3的峰值应力降低,由47.93 MPa减小到30.18 MPa,这与表3所示的抗压强度试验结果一致。此外,峰值应变随着橡胶掺量的增加而增大,由0.001 6增大到0.002 7。取峰值应力的10%和30%之间的割线模量作为试件的弹性模量,其随着橡胶掺量的增加而降低,下降幅度约为16.3%~26.9%。
橡胶颗粒具有较低的弹性模量和较强的变形能力,使得RSCC的峰值应力和弹性模量均小于SCC,而橡胶本身在基体中可以阻止裂缝扩展,提高SCC的变形能力,从而显著增强其韧性。
2.1.2 不同橡胶尺寸
不同橡胶尺寸条件下,试件S3~S5的应力-应变曲线如图4所示,从图4中可以看出,橡胶尺寸为1~2 mm和2~4 mm的试件S3与S4的曲线形状基本相同,仅在下坡段略有差异,而尺寸为0~0.3 mm的试件S5的曲线形状更加“矮胖”。

图4 不同橡胶尺寸下试件S3~S5的应力-应变曲线
随着橡胶尺寸的降低,试件S3~S5的峰值应力由30.5 MPa减小到25.8 MPa,弹性模量由25.7 GPa减小到23.2 GPa,这与抗压强度结果类似。此外,试件的峰值应变则由0.003 5增大到0.003 7。
橡胶粉相比于橡胶颗粒其比表面积更大,在基体中形成界面过渡区面积更大。此外,如表3所示,随着橡胶尺寸的降低,基体的含气量逐渐增大。更大面积的弱界面过渡区和更高的含气量是试件的峰值应力和弹性模量降低的主要原因。广泛分布在基体中的橡胶粉能够阻止微裂缝扩展,延缓新裂缝出现,提高其变形能力[12]。
2.1.3 不同应变率
不同应变率条件下,试件S0和S3的应力-应变曲线如图5所示,从图5中可以看出,随着应变率增加,试件的峰值应力逐渐增大,峰值过后,试件的应力快速衰减,且应变率越大,衰减速度越快,而试件S3的下降段相比于S0更平缓。

图5 不同应变率下试件S0和S3的应力-应变曲线
当应变率由10-5s-1增大至10-2s-1时,试件S0的峰值应力由47.9 MPa增大至62.4 MPa,峰值应变由0.001 6下降至0.001 33,弹性模量由34.9 GPa增大至40.2 GPa,试件S3的峰值应力由30.18 MPa增大至45.96 MPa,峰值应变由0.002 8下降至0.002 4,弹性模量由25.4 GPa增大至32.2 GPa。
不同应变率条件下,试件的峰值应力、峰值应变和弹性模量与应变率的关系可以由下式进行研究,即[22]
f/fs=a+blg(θ/θs)
(1)
式中:f和fs分别为试验和准静态条件下的力学指标;a、b为相关参数,其中b为应变率的敏感系数;θ和θs分别为试验和准静态条件下的应变率。
为了分析试件S0和S3的峰值应力、峰值应变和弹性模量与应变率之间的关系,以10-5s-1为准静态条件下的应变率,根据式(1)建立力学指标与应变率之间的关系如图6所示,从图6中可以看出,试件S0和S3的峰值应力应变率敏感系数绝对值最大,弹性模量次之,峰值应变最小。

图6 力学指标与应变率的关系
从图6(a)可以看出,试件S0和S3的峰值应力随着应变率的增加而增大,表现出明显的应变率增强效应。根据王攀峰等[23]研究结果可以看出,当应变率较低时,基体中的裂缝主要沿着界面过渡区拓展,峰值应力的大小主要取决于界面过渡区的强度,而随着应变率的增大,基体中的裂缝来不及扩展,裂缝直接劈穿骨料,此时试件峰值应力的大小主要取决于骨料的强度,因此试件S0和S3的峰值应力随应变率的增加而增大。
由图6(b)可以看出,试件S0和S3的峰值应变随着应变率的增加而减小,表现出应变率减弱效应,这也与韩辰悦等的研究结果一致[24]。由于随着应变率的增大,试件的峰值应变的决定因素从基体转化为骨料,而骨料的变形小于基体,所以试件的峰值应变随应变率的增大而降低。
从图6(c)可以看出,试件S0和S3的弹性模量随着应变率的增加而增大,与峰值应力类似,也表现出应变率增强效应。随着应变率的增大,试件中微裂缝的扩展受到限制,导致基体的变形减小,从而增大了其弹性模量。
2.2 能量演化规律
2.2.1 能量转化原理
由热力学定律可知,材料破坏是能量驱动下的状态失稳现象[25]。在荷载作用下,外力对试件做功产生的总应变能(不考虑该物理过程与外界的热交换)将转化为试件内部的弹性应变能和耗散能,由热力学第一定律可知
U=Ud+Ue
(2)
式中:U为外力对试件做功产生的总应变能;Ud为耗散能;Ue为弹性应变能。
根据应力-应变曲线可知,外力对单位体积试件做功产生的总应变能为
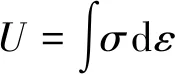
(3)
式中,σ和ε分别为试件的轴向应力和应变。
弹性应变能和耗散能可根据应力-应变曲线求得,如图7所示。假设试件的未损伤部分与损伤部分相互独立,材料未损伤部分的抗变形能力由弹性模量表征,在加载过程中,试件得到的平均弹性模量近似等于试件的初始弹性模量[26]。单位体积试件的弹性应变能Ue和耗散能为Ud可以表示为

图7 能量划分示意图
(4)
(5)
式中,E为试件的初始弹性模量,文中取峰值应力的10%~30%的割线模量为初始弹性模量。
2.2.2 能量演化特征
混凝土材料的能量演化特征曲线如图8所示,主要分为4个阶段[27]:①压实阶段,初始裂缝在荷载作用下闭合,总应变能、弹性应变能和耗散能均较小;②弹性阶段,新裂缝未产生,弹性模量未发生退化,耗散能较小,总应变能几乎都转化为弹性应变能;③裂缝快速扩张阶段,新裂缝逐渐产生,总应变能部分转化为耗散能,弹性应变能增速放缓;④裂隙贯通阶段,贯通裂缝产生,混凝土破坏,弹性应变能以耗散能的形式被释放,耗散能快速增大。
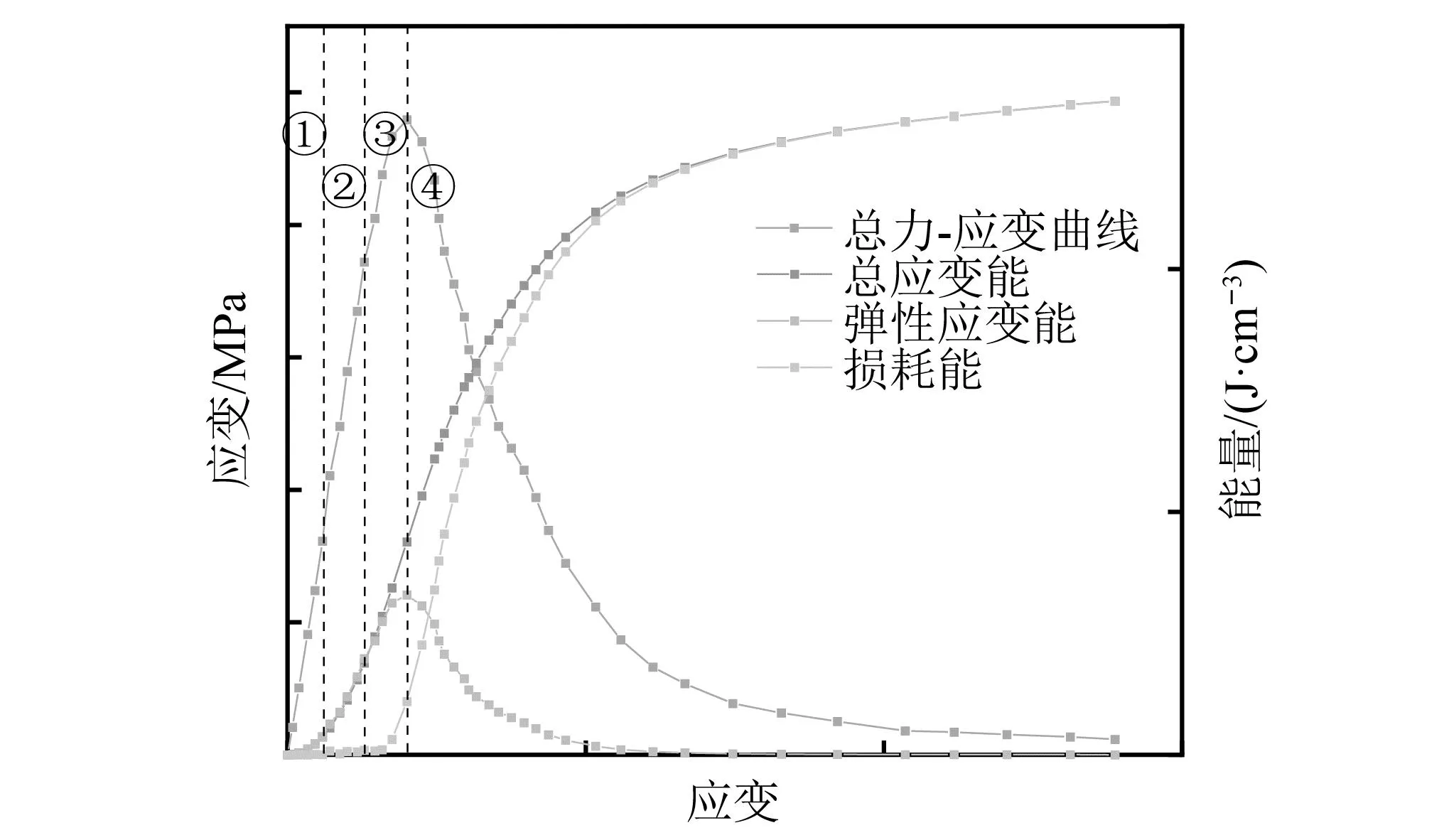
图8 能量演化特征曲线
2.2.3 不同橡胶掺量和尺寸
不同橡胶掺量和尺寸条件下,试件S0~S5的能量演化曲线如图9所示。从图9中可以看出,在初始变形阶段,由于试件S0的初始弹性模量大于试件S1~S5,此时总应变能几乎全部转化为弹性应变能,损耗能几乎可以忽略,因此试件S0的总应变能和弹性应变能均大于试件S1~S5。随着变形的增大,橡胶阻碍了裂缝的扩展,相比于试件S0,试件S1~S5的损耗能增速更慢,损耗能更低。峰值应力以后,试件S0内部产生贯通裂缝,弹性模量快速退化,弹性应变能迅速降低,而橡胶延缓了试件S1~S5裂缝的贯通,弹性应变能释放速度更慢,但总应变能和耗散能依然能够快速增加。到达最终变形时,与试件S0相比,S1、S2、S3、S4和S5的总应变能提高了27.2%、34.8%、44.5%、41.1%和53.8%,耗散能分别提高了26.9%、34.1%、43.1%、39.1和53.4%。

图9 S0~S5的能量演化特征曲线
总的来看,RSCC试件早期的总应变能、弹性应变能和耗散能的发展相比于SCC试件更慢,在峰值应力后,橡胶阻碍了弹性应变能的耗散,延长了总应变能和耗散能的快速增长。
2.2.4 不同应变率
不同应变率条件下,试件S0和S3的能量密度曲线如图10、图11所示。试件S0和S3的总应变能演化规律如图10(a)和图11(a)所示,从图中可以看出,在初始变形阶段,试件内部未产生伤损,弹性模量未退化,应变率变化对总应变能增长的影响不大,而随着进入裂隙贯通阶段,随着应变率的增大,试件S0和S3的总应变能均增大。

图10 不同应变率下S0的能量密度曲线
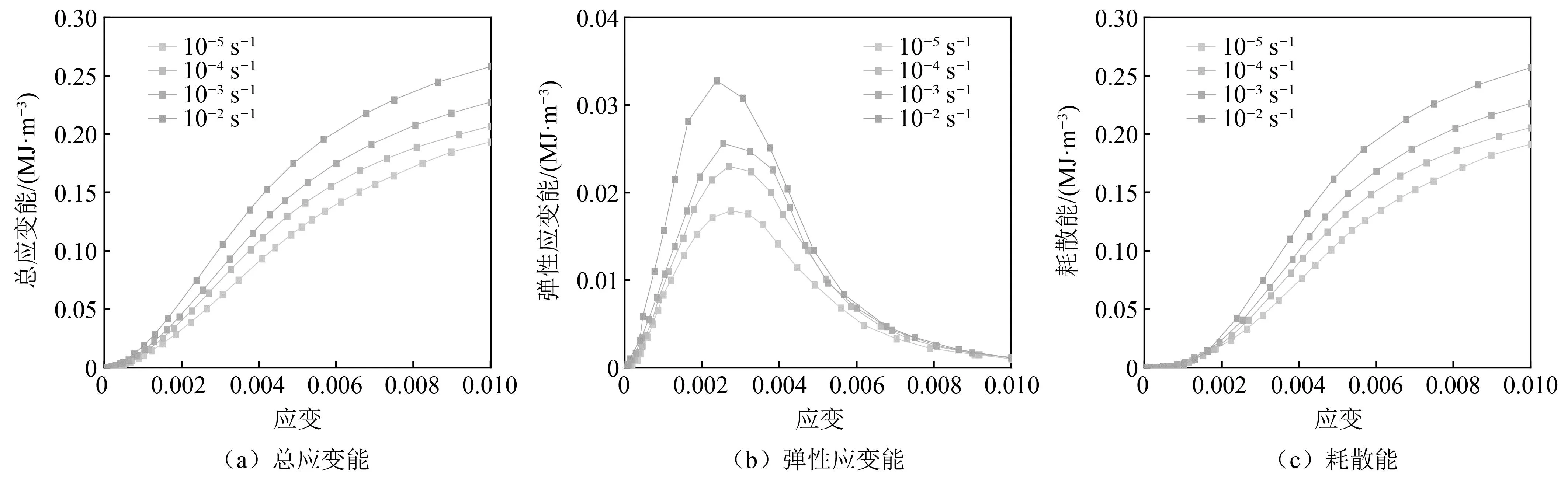
图11 不同应变率下S3的能量密度曲线
不同应变率条件下,试件S0和S3的弹性应变能演化规律如图10(b)和图11(b)所示,从图中可以看出,试件的弹性应变能在峰值应力以前持续增大,当达到峰值应力后,弹性应变能达到最大值,且随着应变率的增大,试件S0和S3的峰值弹性应变能也逐渐增大,峰值应变后,弹性应变能不断减小,且应变率越大,弹性应变能的释放速率越大。
不同应变率条件下,试件S0和S3的耗散能演化规律如图10(c)和图11(c)所示,从图中可以看出,在裂缝快速扩张之前,试件的耗散能几乎没有增加,总应变能几乎全部转化为弹性应变能储存在试件中,当裂缝快速扩张时,耗散能迅速增加,峰值应力后,耗散能持续增大,且应变率越大,耗散能的增速越快,这也表明了试件的脆性破坏特征越明显。
3 基于能量耗散的本构模型
3.1 本构模型的建立
根据Lemaitre的应变等价性假说,名义应力作用于损伤材料产生的应变响应与作用于未损伤材料的有效应力产生的应变响应相等[28]。因此,用有效应力代替名义应力可以得到材料的损伤本构关系
σ=σ*(1-D)=Eε(1-D)
(6)
式中:σ和σ*分别为名义应力和有效应力;D为损伤变量;E为材料弹性模量;ε为材料的应变。
由统计损伤力学可知,SCC可近似等效为无数细小微元组成的系统,损伤程度可由破坏微元数量占总微元数量的比值表示,此外,SCC的损伤程度与能量耗散有关。由于混凝土是各种矿物材料和胶凝材料的混合物,具有明显的非均质性,其力学性能呈现出随机分布的特点,产生的损伤也随机分布在混凝土材料中。因此,假设SCC的微元破坏概率与耗散能之间满足 Weibull 的概率密度关系,即
(7)
式中:p(Ud)为概率密度函数;n和m为Weibull的分布参数。
能量耗散达到一定水平时,SCC中破坏微元的数目为
(8)
式中:N为SCC内已破坏微元的数量;Nt为SCC内总微元数量。
损伤变量D为破坏微量占总微量元素的比例,即
(9)
将式(9)代入式(6)便得到基于能量耗散的SCC本构模型,即
(10)
3.2 本构模型的验证
将等式(10)左右两边分别取对数可得
(11)
将等式(11)左右两边再取对数可得
(12)
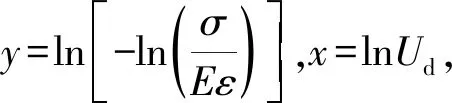
y=nx-c
(13)
式中:c=nlnm,通过将试验数据变换并线性拟合便可得到n、c,即
(14)
通过计算得到的本构模型参数如表4所示,具体拟合曲线见图12和13所示。

表4 本构模型相关参数

图12 试件S0的计算值与试验结果对比
从图12~图13中可以看出,不同应变率条件下,试件S0和S3的计算值与试验结果具有较强的一致性,本构模型能很好模拟压实阶段、弹性阶段和裂缝快速扩展阶段,仅在缝隙贯通阶段,本构模型高估了试件S0和S3的延性变形特征。
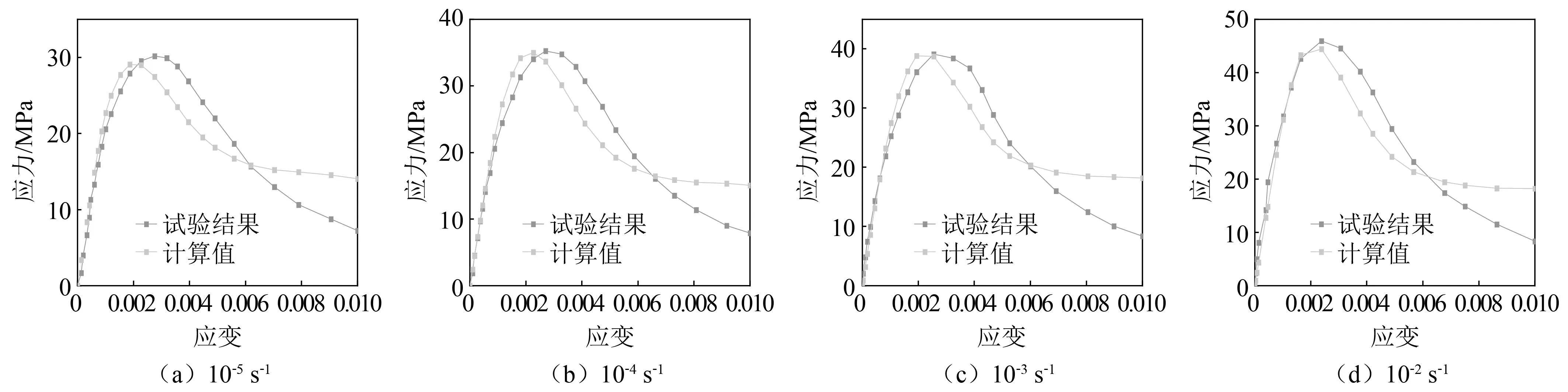
图13 试件S3的计算值与试验结果对比
此外,文献[12]中自密实混凝土和橡胶自密实混凝土的配合比、强度等级以及橡胶掺量范围与本试验相近,因此,图14将本文提出的本构模型与文献[12]的试验结果进行比较,从图14中可以看出,本构模型计算结果与文献[12]的应力-应变曲线试验结果具有较好的一致性,仅高估了试件的延性变形特征。综上所述,本文基于能量耗散建立的本构模型能很好表征地铁板式轨道自密实混凝土以及橡胶自密实混凝土的应力-应变关系。

图14 文献[12]的应力-应变曲线与本构模型计算结果的对比
4 结 论
(1)SCC和RSCC的峰值应力、弹性模量和峰值应变都表现出明显的应变率效应,其中峰值应力应变率敏感系数绝对值最大,弹性模量次之,峰值应变最小。
(2)随着橡胶掺量的增加和尺寸的降低,试件早期的总应变能、弹性应变能和耗散能的发展更慢,在峰值应力后,橡胶阻碍了弹性应变能的耗散,延长了总应变能和耗散能的快速增长。
(3)在加载初期,应变率对SCC和RSCC的总应变能和耗散能影响不大,峰值应力之后,随着应变率的增加,试件的总应变能和耗散能均增大。此外,随着应变率的增加,试件的峰值弹性应变能也逐渐增大,峰值应变后,弹性应变能不断减小,且应变率越大,弹性应变能的释放速率越大。
(4)基于能量耗散建立的本构模型,可以用于描述地铁板式轨道充填层SCC和RSCC在不同应变率条件下的本构行为。

