二维层状盆地地震动附加放大特征研究:SV波入射
于彦彦, 丁海平, 芮志良
(苏州科技大学 江苏省结构工程重点实验室,江苏 苏州 215011)
沉积盆地作为一种典型场地,在中国及世界有广泛的分布,比如墨西哥盆地、洛杉矶盆地、北京盆地、福州盆地及我国山地地区诸多的山间小型盆地等。在其形成过程中,盆地的低凹基底使其接受了来自周边区域的大量松软覆盖层的堆积,导致盆地内外介质刚度的显著差异。同时,一般的沉积历史常使得盆地沉积层具有从地表向下逐渐变硬,波速逐渐增大的特征。
盆地对地震动的显著放大作用已成为地震工程领域的共识。研究者通过观测数据、理论解析及数值模拟等方法来探究盆地对地震动的放大特征,并取得丰硕成果[1-4]。其中,基于观测记录的分析方法多采用盆地外的基岩台站记录作为参考,利用盆地内部台站相比参考台站的地震动峰值或频谱/反应谱之比来研究盆地的放大效应[5]。该技术同样在数值模拟方法中采用,但后者除了用盆地外基岩台站作为参考台站外,还有采用无盆地的基岩半空间模型[6]、无盆地的水平土层模型[7]及入射地震动[8]作为研究盆地放大作用的参考模型。而解析方法多以盆地地表地震动相比入射波在频域中的放大为研究对象。
对于沉积盆地之上工程结构的地震安全性评价,土层地震反应分析是其中的重要组成部分。目前土层地震反应分析仍多采用基于一维土层模型的等效线性化方法。该方法在关心的场地范围内取若干控制点,然后通过钻孔、室内试验等方法获取场点处一定深度内的土层参数(如波速、动剪切模量等),进而建立土层模型,采用一维等效线性化方法(常用程序如国外的SHAKE、DEEPSOIL及国内的LSSRI等)模拟设定地震波输入下场点地表处的地震动响应,从而服务于该场地之上结构的抗震设计。但这一方法没有考虑盆地横向速度构造的不均匀性,如盆地特殊的几何形状及盆地内外介质波阻抗的显著差异。既有研究表明这一不均匀性会在盆地内形成次生的Rayleigh或Love面波(这些次生面波在向盆地内传播的过程中与直达体波的叠加干涉会显著放大盆地边缘区域的地震动,形成“盆地边缘效应”)[9-10],及一定条件下的盆地共振效应[11]、聚焦效应[12]等,这些都是一维土层模型所无法再现的,一维模型往往低估场地地震动强度及持时。如金丹丹等[13]对比了福州盆地不同场点处采用二维非线性模型和一维等效线性化模型在地震波输入下的地震动特征的差异,结果显示二维盆地才能表现出特定频段地震波的显著放大效应与聚焦效应。Day等[14]研究了洛杉矶盆地在60个设定断层破裂情况下的盆地反应谱平均放大效应(以一维基岩成层场地为参考模型),发现和一维的理论预测相比,三维结果普遍更大,放大系数随深度和周期的变化也更为平滑。Zhu等[15-16]和Riga等[17]研究了平面SH和SV波入射下二维盆地模型各场点处相比一维土层的地震动附加放大特征,但主要考虑的是盆地内为均匀介质的情形。Riga等[18]补充考虑了盆地内介质剪切波速的梯度变化的影响,但没有考虑纵波波速沿盆地深度的变化。同时,以上研究中对于附加放大系数对输入波的敏感性的研究相对较少。考虑(GB50011—2010)《建筑抗震设计规范》[19]对于沉积盆地场地的工程抗震设计尚未作详细要求,且盆地场地地震安全性评价中仍常用一维土层模型,因此非常有必要对盆地模型相比盆地各场点处的一维土层模型地震动的差异程度及附加放大特征进行研究。
在基于数值模拟方法的盆地地震效应研究中,谱元法以其高精度、低频散的特性而得以广泛应用[20]。相比传统高阶有限元法,谱元法内置勒让德或切比雪夫积分点为谱元节点,在提高了模拟精度的基础上,显著降低了模拟中的数值频散,同时具有良好的收敛性。与此同时,为减少计算量,常常需要从无限域地基中截取有限的计算区域,并在截断边界上施加某种人工边界条件来模拟外行波的透射过程,常采用的如黏性边界、黏弹性边界、多次透射边界、完美匹配层等。其中多次透射边界(multi-transmitting formula,MTF)具有无需区分波场类型、可实现高阶精度、基本不增加计算量等优点,因此已有研究者将其引入到基于谱元法的波动数值模拟中并取得良好的效果[21-24]。如Yu等[24]对比了分别采用有限元法和谱元法结合透射边界的方法对于平面SH波散射问题的模拟效果,结果显示MTF在谱元法中具有比在有限元法中更好的高、低频稳定性表现。
对于平面波入射下局部场地或结构的波动散射问题,目前常用的方法包括:有限元法结合黏弹性边界[25-26]、有限元法结合透射边界[27-28]、有限差分法结合自由场边界[29]、边界元法[30-31]及各种混合方法[32-33]等。相比既有的数值方法,本文方法兼具了谱元法与多次透射边界的优势:①相比线性有限元法,谱元法具有高阶精度,在同等精度条件下所需网格数相对更少。②相比高阶有限元,谱元法内节点的合理选取使其在抑制Runge现象及数值模拟伪波方面具有良好的表现。③与低阶精度的黏弹性边界相比,MTF可实现二阶、三阶甚至更高阶精度。④相比边界元法,谱元法适用于任意的复杂地形及介质本构模型。最后,MTF在传统有限元法中较易出现高频振荡和低频飘移失稳,而谱元法的低频散特征使得MTF具有相比在有限元法中更好的稳定性。
在以上研究的基础上,本文首先发展了一种结合高精度谱元法和多次透射边界的平面SV波入射下一维和二维散射问题波动数值模拟方法,并基于数值算例验证了方法的精度和稳定性。在此基础上,从工程角度出发,详细研究了二维梯形成层盆地场地相比盆地各场点处对应的一维土层模型在31条不同地震波(SV波)垂直输入下地表地震动的附加放大特征。为减少方法的不同引起的模拟结果的差异,本文中一维土层和二维盆地模型的地震动响应均采用谱元法模拟。
1 模拟方法及其精度和稳定性验证
本文采用一种结合高精度谱元法和多次透射边界的散射问题波动数值模拟方法来模拟平面SV波入射下二维复杂场地的地震动响应。模型示意图如图1所示。地表存在局部非规则散射体(如山体、盆地等),地表之下为层状分布的土层,模拟平面波垂直入射时的地震动响应。以下对本方法的基本原理和过程进行介绍。
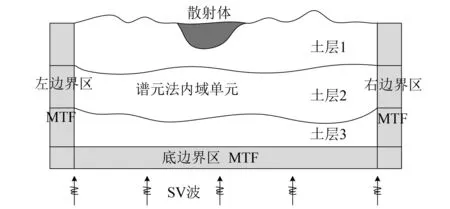
图1 二维复杂场地模型示意图
1.1 模拟方法
1.1.1 一维参考波场的谱元法求解
一维参考波场或自由场(即广义散射体不存在时入射波在成层半无限域中产生的波场)的精确模拟是影响本文方法模拟精度的关键之一。本文采用匹配二维网格节点和模拟精度的Legendre谱元法计算地震波垂直入射下一维土层(图1中左、右边界区)的地震响应,并将其作为二维复杂模型在平面波入射下的地震响应的入射自由场。
对一维谱元法,在单元层级上波动方程的等效积分弱形式为

(1)
式中:ρ为介质密度;υ为试函数;u为待求解的位移,f为广义外力。
对式(1)左端第一项采用GLL数值积分法求解(积分点取为±1及N阶Legendre正交多项式一阶导数的零点)后可得单元质量阵[34],即
(2)
式(1)左端第二项采用同样的数值积分法可得
(3)
对SV波输入下的地震响应求解问题,式(1)右端f=0。
求得单元质量阵和刚度阵后,对运动方程式(1)进行空间离散可得节点i的运动方程为
(4)
式中,e和j为与节点i关联的所有谱单元和节点编号。
忽略单元内加速度的变化,即假定与节点i相连的每一单元各个节点的加速度都等于节点i的加速度[35],即

(5)
将式(5)代入式(4)可得谱元节点i的运动方程为
(6)
设集中于谱元节点i的质量为mi,有
(7)
(8)
一维模型边界节点(亦为波动输入点)的运动采用1.1.3节中的方法求解。基于上述方法编制程序即可实现平面SV波入射下基于谱元法的一维土层波动响应(即参考波场或自由场)的模拟。
1.1.2 二维模型内节点运动的谱元法求解
对多维问题,谱元法一般直接求解节点本构力而无需计算类似式(3)的刚度矩阵,这样一方面可以提高计算效率,另一方面便于荷载和边界条件的施加。二维谱元法波动方程等效积分“弱”形式为

(9)
式中:u为平面波入射时引起的位移场,u=[uxuz]T;σ为作用于单元节点的应力张量,σ=c·∇u,c为介质的弹性张量(可为线弹性或黏弹性);∇为梯度算子;f为集中于节点的外力;ρ为介质密度。
将方程式(9)中第一项进行等参变换并采用GLL数值积分可得[36]
(10)

同理,对方程式(9)中第二项采用GLL数值积分可得
(11)
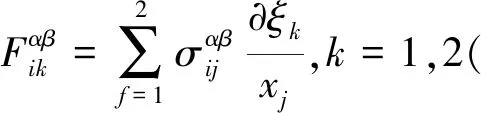
对所有单元进行装配后可得全部谱元节点的运动方程为
(12)
基于上述原理,本文内节点的运动采用开源谱元程序SPECFEM2D(https:∥github.com/SPECFEM/ specfem2d)模拟。程序由Komatistch等基于谱元法理论,在Linux系统下采用Intel Fortran语言开发,可用于模拟地震破裂或其它形式动荷载引起的近场波动反应。程序通过引入MPI技术,可进行波源问题(即震源位于模型内部)下大区域场地地震动的并行计算,其介质可考虑线弹性、线性黏弹性、流固耦合等情况。
1.1.3 边界节点运动的模拟
边界节点的运动可视为输入计算域的内行波,与局部散射体引起的向外辐射离开计算域的外行波的叠加。其中对后者可采用人工边界条件进行模拟。本文采用多次透射公式(MTF)模拟外行波的传播过程。考虑谱元法中节点分布不均匀的特点,在Yu等SH问题的基础上实现平面SV波散射问题下MTF与谱元法的结合。
如图2所示(图中虚线范围为1个谱单元,黑色实心圆圈表示谱单元节点,空心圆圈表示计算点位置),根据MTF理论,边界节点0在(p+1)时刻的外行波场的位移(水平和垂直向)由之前若干时刻计算点的外行波场位移外推得到,即

图2 二维谱元节点及MTF计算点示意图
(13)
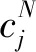
由于计算点与谱元节点的位置一般不重合(见图2),而谱元法求解得到的是节点位移,因此,计算点的散射场位移可由边界单元法线上NGLL(NGLL为GLL点的个数)个谱元节点同时刻的外行波场位移按Lagrange插值法得到,插值公式为
(14)

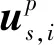
(15)
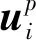
(16)
该过程在垂直和平行边界2个方向上同时进行。基于式(13)~式(16)即实现谱元法中外源问题的波动输入及边界节点位移的递推求解。内节点的位移采用式(12)求解,进而可模拟得到平面SV波入射下二维复杂场地的地震动响应。
1.2 方法的精度和稳定性验证
取验证模型为一均匀半空间之上的半圆形凹陷地形如图3所示,其半径a=50 m,介质剪切波速500 m/s。模型尺寸1 000 m×240 m。输入宽度为0.2 s的脉冲波,其时程及频谱如图4所示。模拟时间步距0.2 ms,总时长260 s(130万步)。模拟中不采取任何抑制高频振荡失稳的措施。
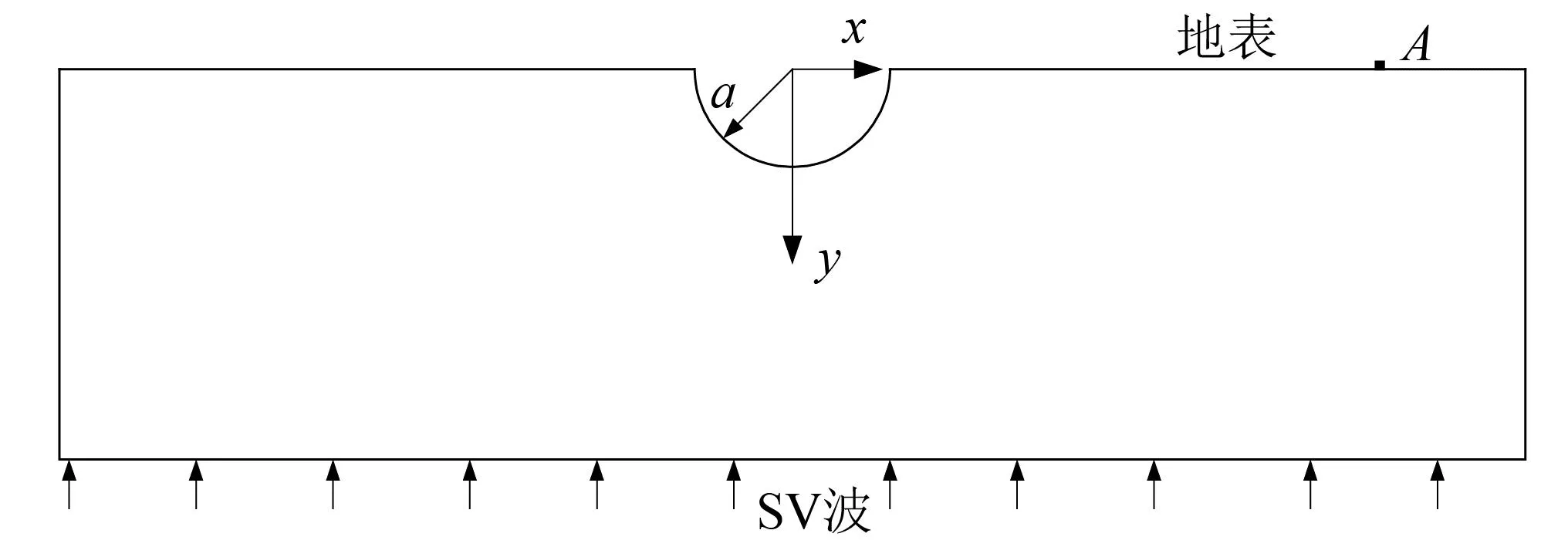
图3 半圆形凹陷地形模型

图4 用于精度验证的输入波时程(上)及其傅里叶幅值谱(下)
将模拟得到的无量纲频率(无量纲频率定义为,为入射波波长,其对应的频率为10 Hz)对应的地表各点的谱放大系数和 Wong[37]巴振宁等[38]的结果对比于,如图5所示。可以看出,本文结果与参考解吻合良好,很好地再现了局部凹陷地形对于特定波长地震波的放大特征,显示出本文方法在模拟SV波入射下局部地形对地面运动影响的较高精度。图6给出了坐标为(400,0)的观测点A的模拟位移时程,为对比起见,图中同时给出了采用MTF和有限元法的模拟结果。可以看出,在未施加抑制措施的条件下,直至260 s(为清晰起见图中仅给出0~10 s的结果),MTF在谱元法中依然未出现高频振荡失稳,主反应时程后的波动值始终维持在0附近。对比而言,采用MTF结合传统有限元法的结果在计算至6 s左右时即开始出现振荡现象。MTF在谱元法中良好的高频稳定性可能主要与谱元法的特定空间离散形式的低频散特性有关。
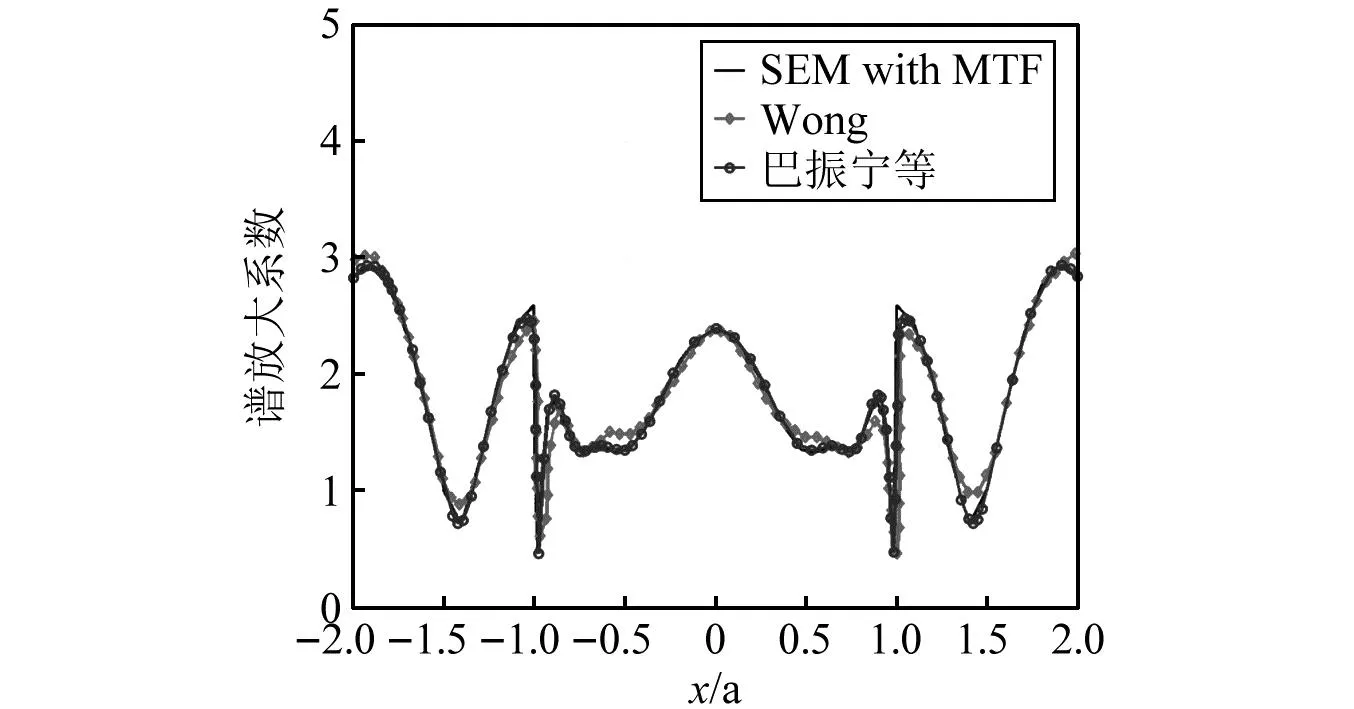
图5 半圆形凹陷地表各点的谱放大系数与既有结果的对比
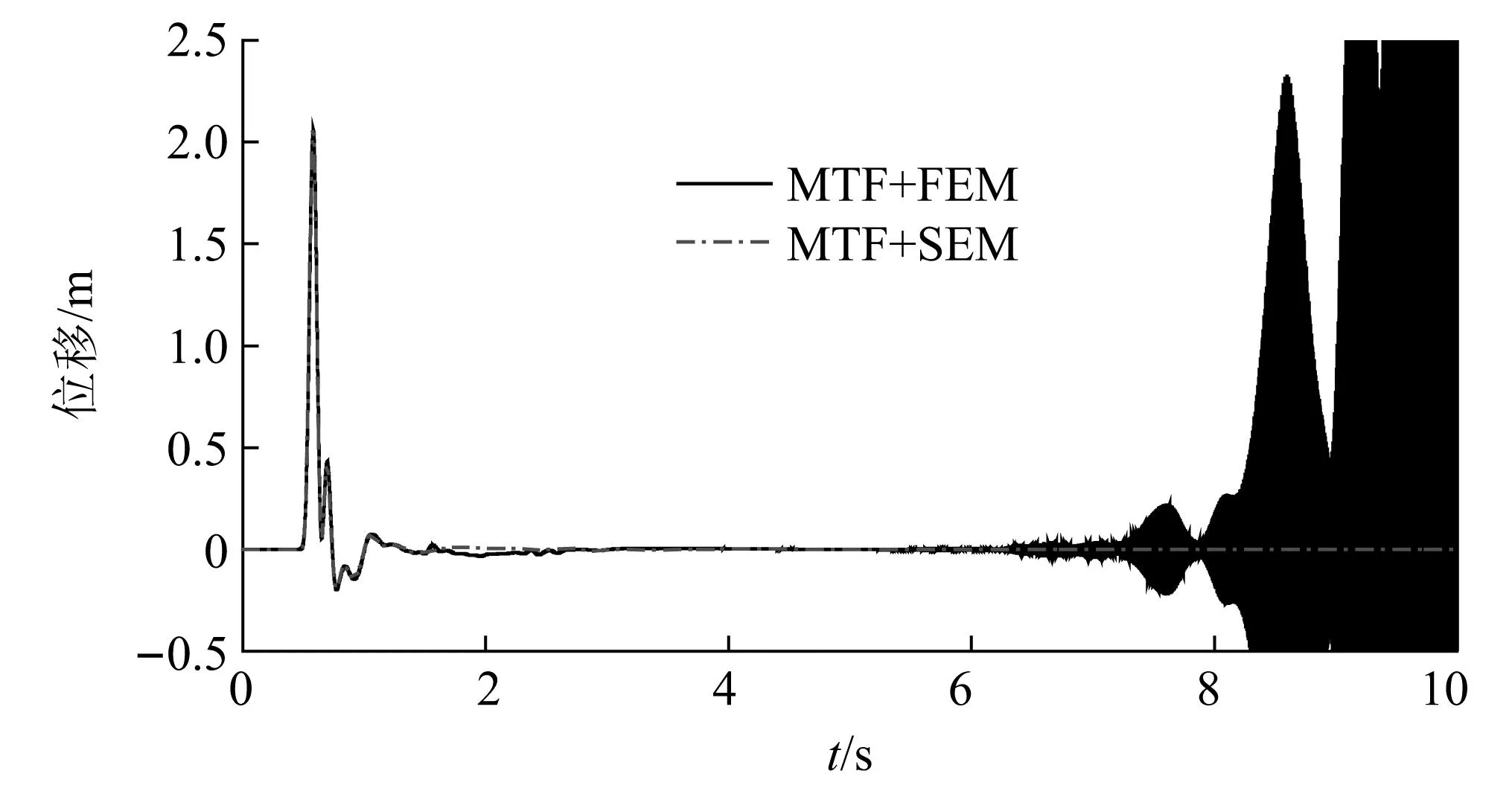
图6 不同方法模拟的观测点A的位移时程
以上结果表明本文方法对于二维复杂场地在平面SV波入射下的地震动响应问题具有较高的模拟精度,且具有更好的高频稳定性表现,可用于下一步的平面SV波入射下二维盆地地震动放大特征的研究。
2 盆地模型与入射波选取
参考Asimaki等[39]针对墨西哥城盆地所建立的一条测线的二维剖面模型,建立典型梯形盆地模型如图7所示。图中黑色三角形表示观测点位置,共计81个观测点(编号为1~81),观测点间距为50 m。考虑盆地内覆盖层的沉积过程,盆地内部土层由上至下分为三层。盆地地表处最大宽度4 km,盆地最大深度200 m。该盆地尺寸与我国西南地区的部分山间小型盆地(如施甸盆地等)的尺寸接近。盆地及基岩介质参数如表1所示。其中为考虑介质衰减的影响,取S波品质因子为剪切波速的0.1倍,P波品质因子为该值的2倍。为研究二维盆地相比一维土层由于盆地基底特殊的几何形状引起的附加放大效应,取地表点至基岩处对应的一维土层为参照模型,其介质参数与盆地模型完全相同,并将其定义为一维等效土层模型(如图7(b),(c)所示)。划分盆地模型的最小网格尺寸为10 m,结合盆地内介质的波速分布,该模型能模拟的最高频率约为10 Hz。

表1 模型介质参数
(17)
考虑输入地震动的随机性特征,以及仅输入单一的特定波时盆地的共振现象或高阶模态面波可能不会被激发[43]等,从PEER网站(https:∥ngawest2.berkeley. edu/)选取了全球范围内9次典型地震中的31个典型基岩台站的加速度记录作为输入波,以更好地统计盆地的放大效应,其详情如表2所示。台站记录的加速度时程如图8所示,图中每条地震波的左侧为其对应的加速度峰值(peak ground acceleration,PGA),右侧为对应的台站名。为显示方便各时程已用其PGA进行了归一化处理。可以看出,这些地震记录在震源机制、断层类型、震中距、幅值、频谱、持时等方面均具有显著差异。

表2 输入地震波详情

图8 作为入射地震波的台站记录加速度时程
由图8可知,31条输入波中,27条波的PGA位于(0,200)gal的范围,2条位于(200,500)gal的范围,其余2条大于500 gal。考虑台站记录的为自由地表的响应,在作为盆地模型的基底输入时还需考虑自由地表的放大效应,本文采用简化方法,将以上地震波的时程除以2作为盆地模型的输入波,此时绝大部分入射波的PGA在100 gal以下。在此入射地震动强度下,将盆地内沉积层简化为黏弹性介质(即不出现明显非线性反应)具有一定的合理性。同时,为减少土体本构模型及计算方法的不同引起的结果差异,本文中二维盆地和一维等效土层模型均采用相同的黏弹性本构和谱元与透射边界相结合的方法进行模拟。
图9给出了所有入射波的反应谱,其中加粗的点划线和虚线分别对应于3.1节中拟进行对比的NORTHR_PAC175和CHICHI_HWA003-N两条输入波的反应谱曲线。

图9 入射地震波的反应谱曲线
3 二维层状盆地相比一维土层地震动放大特征
3.1 不同地震波输入下地表响应时程及放大特征对比
分别选取输入波为NORTHR_PAC175和CHICHI_ HWA003-N(以下分别简称为NORTHR波和CHICHI波),其时程和对应的加速度反应谱见于图8和图9。可以看出二者在幅值、频谱和持时等方面均具有较显著差异,如前者的高频成分相比后者显著得多。两条地震波输入下,二维盆地模型和一维等效土层模型模拟得到的地表81个观测点的加速度反应时程如图10所示,图10中同时给出了各观测点对应的PGA的分布。可以看出,首先,采用一维等效土层模型模拟得到的地表点响应无法反映二维盆地的地震效应,如二维盆地形成的次生面波及其与体波的叠加干涉现象,以及盆地边缘区域相比盆地中心区域的地震动放大现象(盆地 “边缘效应”,图10(a))在一维模型结果中均无体现。其次,对于盆地模型,差异明显的地震动输入下,盆地地表点的加速度响应具有较大差别:首先是盆地边缘形成的次生面波的差异。NORTHR波输入时,地表观测点时程中同时包含基阶和二阶Rayleigh面波,而CHICHI波输入下则仅有基阶面波生成,这主要与相对低频成分为主的输入波激励下盆地中激发不出高阶模态面波有关[44]。其次,不同地震波输入下的次生面波的强度有差异,CHICHI波输入下的面波幅值相对更大。此外,考虑土层的衰减作用时,盆地边缘形成的次生面波在传播过程中的衰减较为明显,尤其是对于NORTHR波输入的情形,面波传播至盆地中间区域时的强度相比盆地边缘时已大为减小。这与盆地内介质采用线弹性本构时的模拟结果明显不同,后者生成的面波可传播至盆地另一侧边缘并在盆地内来回传播,同时对向传播的面波在盆地中心处交汇叠加会明显放大该点处的地震动幅值[45]。
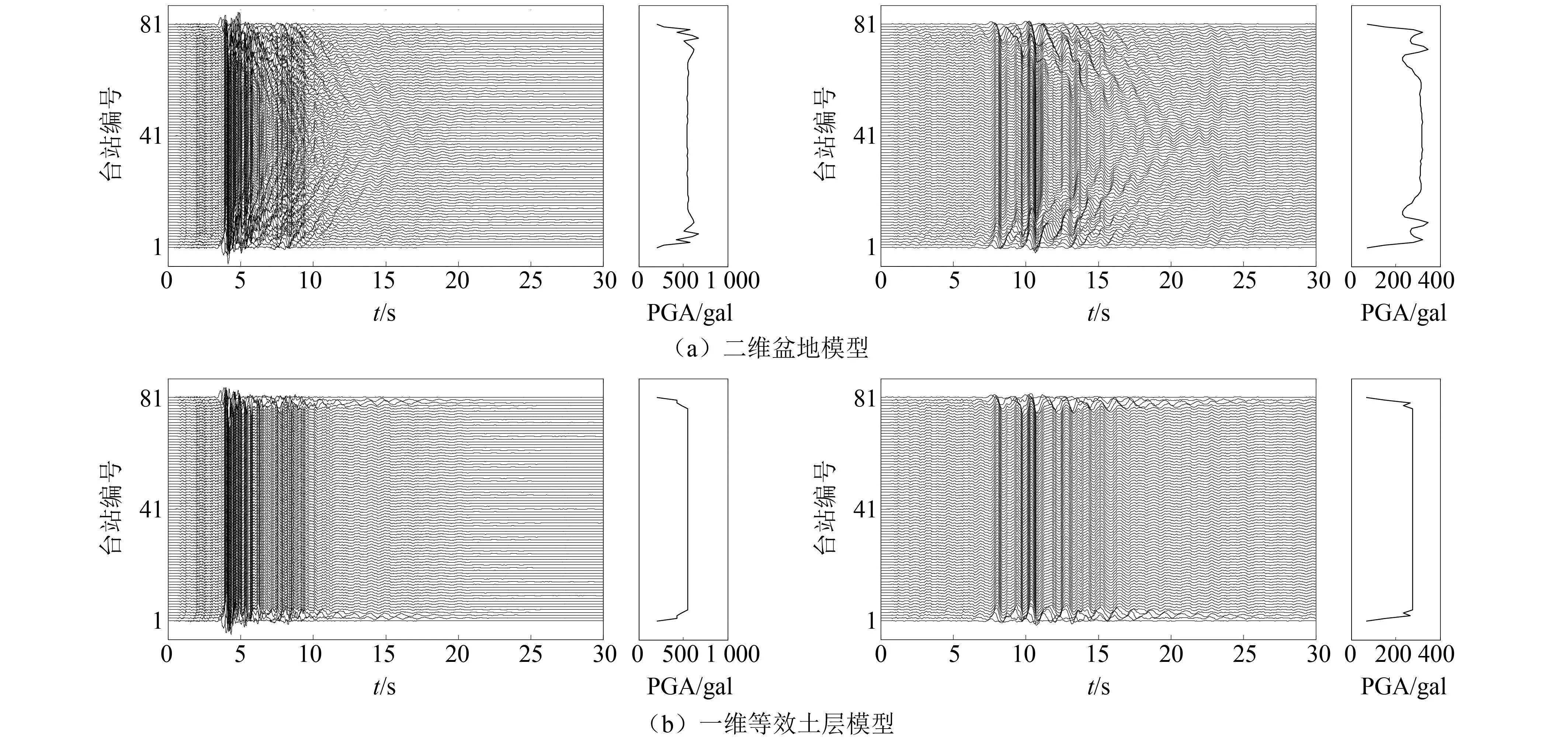
图10 NORTHR_PAC175(左)和CHICHI_HWA003-N(右)地震波输入下地表点加速度时程及PGA分布
定义盆地场地的谱放大系数为相同地震波输入下,盆地模型相比同一场点处的一维等效土层模型地表点加速度反应谱的比值,实际上代表了考虑介质横向刚度变化的二维盆地模型相比横向均匀的一维土层模型模拟地震动的附加放大作用。由于盆地边缘区域的土层厚度变化强烈,而内部区域的土层分布恒定不变,因此观测点1~5及77~81对应的一维土层模型各不相同,其余观测点对应的一维土层模型同观测点5或77处的模型。因此本文模拟的二维模型共31个,一维模型共5×31=165个。
图11给出了NORTHR和CHICHI波输入下盆地地表观测点水平分量的谱放大系数随空间位置和周期的分布情况,其中周期基于盆地最深处的一维土层模型的自振周期(Th=1.43 s)进行了无量纲化。可见二者的谱放大特征亦有显著差别,如NORTHR波输入下,附加放大作用较明显的区域集中在盆地边缘附近(需注意的是紧邻盆地角点的小范围区域内的地震动有缩减效应),盆地内部区域基本无放大(谱放大系数普遍在0.95~1.1之间),而CHICHI波(长周期成分相对更显著)输入下除盆地边缘区域外,在x/L=-0.5~0.5(L为盆地半边长度,即2 000 m),无量纲周期(0.07~0.5)Th及7Th附近的范围内亦有强烈的放大作用。

图11 NORTHR_PAC175(上)和CHICHI_HWA003-N(下)地震波输入下的反应谱放大系数分布
3.2 二维盆地平均反应谱放大系数分析


图12 二维盆地的平均反应谱放大系数分布

对于Z分量,其反应谱放大系数定义为盆地各场点处Z分量加速度反应谱与相应的一维等效土层模型水平分量加速度反应谱之比。从不同输入波下的平均谱放大系数图12(b)可以看出,盆地边缘区域在|x/L|>0.8,T/Th<0.7的范围内均为放大区,最大放大系数可达0.9,出现于x/L= ±0.96(紧邻盆地角点),T/Th=0.28附近的范围。这一显著的竖向地震动对盆地边缘附近结构物(尤其是对竖向地震动较敏感的结构)的抗震设计而言是不容忽视的。盆地中心区域(|x/L|<0.6)垂直分量的放大系数在整个研究周期范围内均在0.1以下(其中盆地中点处为0),对其可不予考虑或在整个周期内采用某一较小的放大系数进行统一考虑。
3.3 二维盆地对不同周期地震波反应谱放大系数分析
为进一步对比盆地对不同周期地震波放大特征的差异,图13给出了31条地震波输入下,盆地地表观测点对于周期分别为0.7 s、1.1 s、1.4 s和5 s的水平分量地震动的反应谱放大系数(spectrum aggravation,SAG)分布。结果显示:盆地对不同周期地震动的反应谱放大特征差别较大,如T=0.7 s时,不同地震波输入下的SAG值普遍大于1,即绝大部分场点处均有放大作用。此外,该周期处的SAG分布存在非常明显的盆地边缘效应,x/L=±0.92附近的SAG值显著大于其余区域。T=1.1 s时,其SAG值相比T=0.7 s普遍减小,部分区域地震动的削减程度增强(如x/L=±0.6时,多达7条地震波输入下的SAG值在0.8以下),但盆地边缘效应依然能够看出。当T=1.4 s(约为自振周期)时,盆地的边缘效应开始变得不明显,同时盆地中点附近的平均SAG值大多在1以下。此外,T=1.1 s和1.4 s时在x/L∈(-0.64,-0.2)及其对称区域范围内,多数地震波输入下的SAG值都明显小于1,这与图12(a)中的结果对应。而对于长周期(T=5 s)地震动,除盆地角点附近依然明显的地震动削减作用外(SAG值明显小于1),其余区域的反应谱放大系数普遍在1左右,且盆地边缘区域与中间区域的SAG值差别较小,表明此周期下盆地的放大效应不明显。
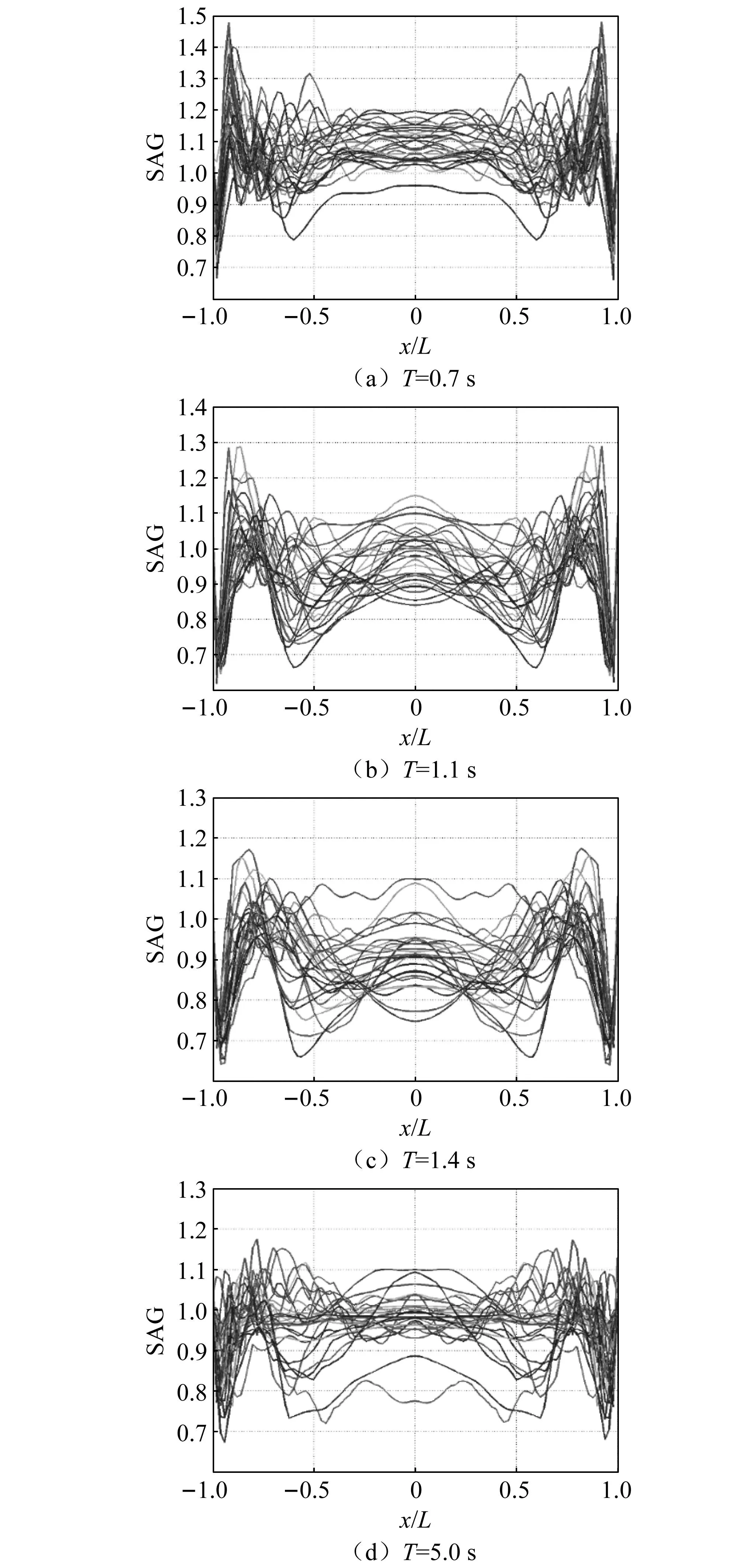
图13 不同地震波输入下二维盆地对于典型周期处的反应谱放大系数分布
图13的结果表明相比一维等效土层模型,二维盆地模型在T/Th≈ 0.5附近的周期段的放大作用最为明显,随周期的增长,这一附加放大作用,尤其是盆地边缘区域的放大作用逐渐减小至较小值。
3.4 二维盆地对不同位置处的反应谱放大系数分析
考察31条地震波输入下,分别位于盆地边缘区域和盆地中心处的2个观测点(5号和41号观测点)对于不同周期段地震波的放大作用,初步分析盆地不同位置处的反应谱放大系数对周期的依赖关系。其结果如图14所示。从图4中可以看出,对于5号测点,在周期0.7~0.87 s的范围内,大部分地震波输入下的SAG值均显著大于1,最大放大系数1.4,而该观测点对于1.5 s以上周期段的谱放大系数普遍在1以下(平均SAG值0.92左右),即其地震动强度相比一维等效土层模型有一定削减。对比而言,位于盆地中心处的41号观测点对2~10 s周期段的谱放大系数大部分在1左右(个别地震波输入下的SAG值在2 s以上周期处存在明显波动),而对于T=0.6~0.8 s范围内的地震动也有一定放大,对应的SAG值在1.0~1.2之间。以上结果表明不同地震波输入下,同一观测点的主要放大周期略有变化,但范围较小,且这一主要放大周期随观测点位置的变化不明显。
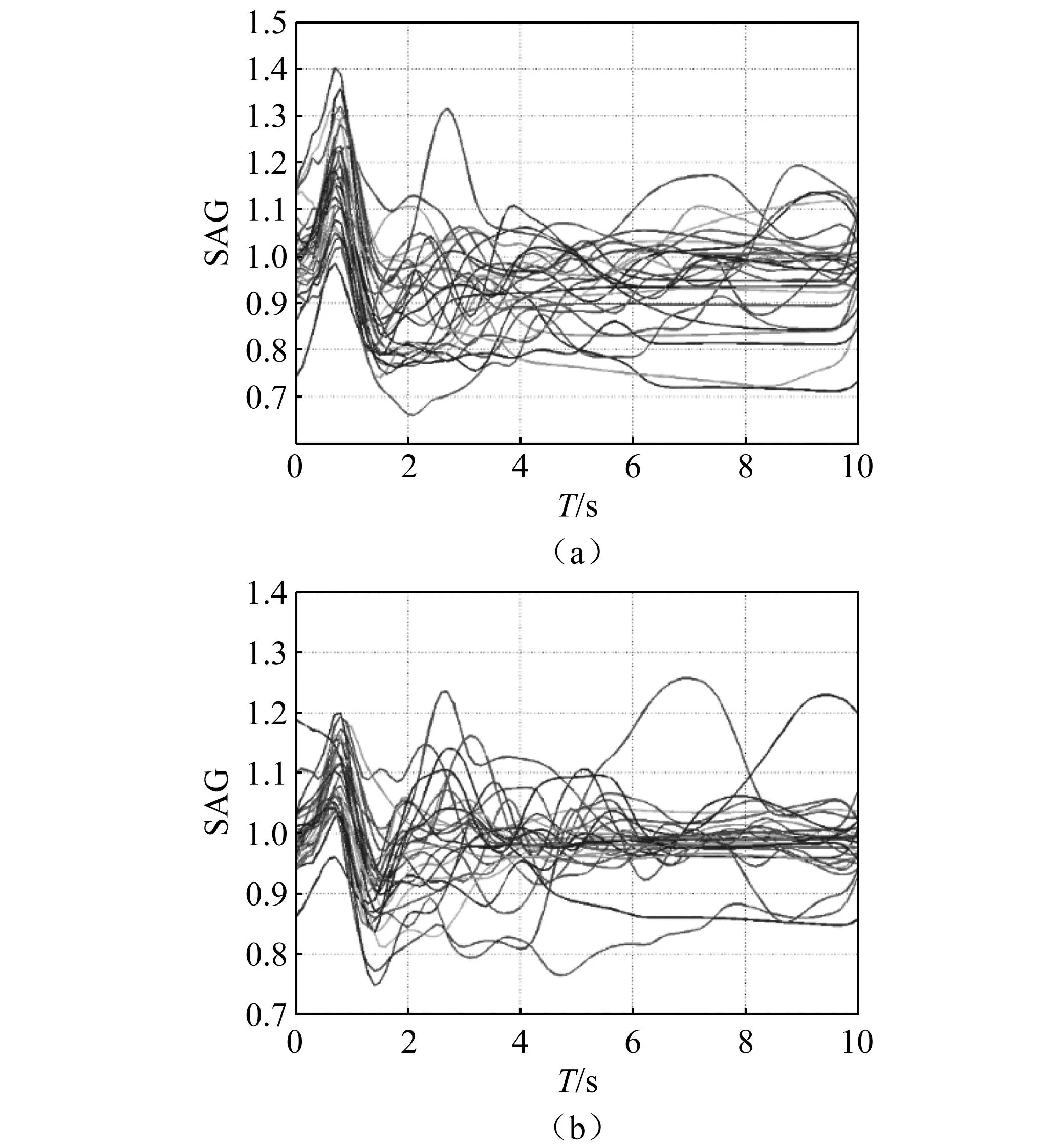
图14 不同地震波输入下5号(上)和41号(下)观测点的反应谱放大系数
3.5 盆地不同位置处的放大系数对输入波的敏感程度分析
从3.3节和3.4节结果中可以看出,不同地震波输入下盆地地震动的放大系数及其分布特征存在不同程度的差异,非常有必要对盆地地表点的放大系数对输入波的敏感程度进行分析。因此,将31条地震波输入下盆地地表各点的加速度峰值放大系数AF(定义为盆地模型地表点的加速度峰值与一维等效土层模型加速度峰值的比值),以及最大反应谱比SAGmax(定义为反应谱比曲线上的最大值)的分布区间用箱型图表示,分别如图15和图16所示。
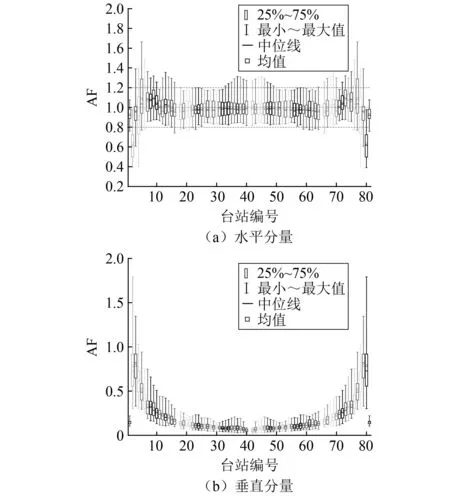
图15 盆地不同位置处加速度峰值放大系数随输入波变化情况
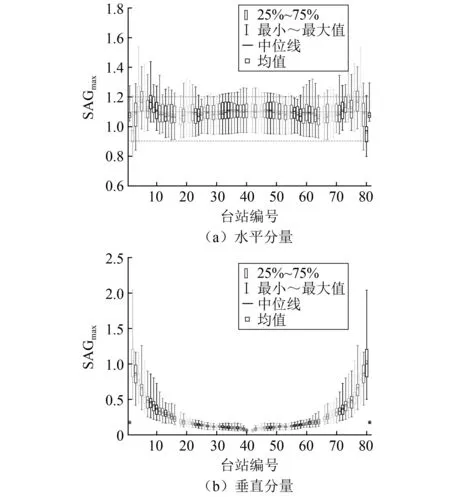
图16 盆地不同位置处反应谱比最大值随输入波的变化情况
由图15、图16可以看出,盆地边缘区域的地震动放大作用对输入波最为敏感,不同地震波输入下的放大系数离散程度较大,且对水平和垂直分量均是如此。以水平分量为例,4号观测点的AF和SAGmax值分别在(0.4~1.4)和(0.9~1.55)的较大范围内变化。同时,相比而言,加速度峰值放大系数的离散程度相比反应谱比最大值的离散程度更甚。而盆地中心区域的放大作用对输入波相对不敏感,AF和SAGmax基本位于0.8~1.2和0.9~1.2之间,均值基本在1和1.08左右,离散程度较小。垂直分量上盆地边缘区域的放大系数离散程度相比水平分量更大,向盆地内部离散程度迅速衰减,邻近盆地中心区域的AF和SAGmax的均值基本恒定在0.1和0.15附近,显示出垂直分量上该区域的放大作用对于输入波相当不敏感。
4 结 论
本文首先将高精度谱元法与具有多阶精度的多次透射边界相结合,用以模拟平面波入射下二维场地的地震动响应。在此基础上,详细研究了不同地震波(平面SV波)输入下,考虑横向不均匀性的二维层状沉积盆地相比各位置点处的一维土层模型的附加放大作用(各点处分别基于两种模型模拟得到的反应谱之比及加速度峰值之比),对比了不同地震波输入下盆地放大特征的差异及各场点对不同周期地震动的放大作用,分析了平均附加放大系数随位置和周期的变化,以及放大作用对输入地震波的敏感程度。基于上述结果可见:
(1)本文方法具有较高精度和良好的稳定性,在波动散射问题模拟中具有较好的应用前景。虽然本文方法是针对二维模型给出的,但其思路同样可用于三维散射问题的分析中。
(2)相比一维等效土层模型,盆地附加放大作用最强烈的区域主要集中在盆地边缘,主要放大周期小于0.7Th(Th为盆地最深处对应的一维土层模型的自振周期),水平和垂直分量上的平均谱放大系数最大值分别为1.2和0.9左右,浮动范围分别为0.9~1.55以及0.5~2.0;两分量的加速度峰值放大系数均值分别可达1.1和0.8左右,浮动范围分别为0.8~1.68以及0.3~1.8。对比而言,邻近盆地中心的区域内的放大作用不明显,其中加速度峰值基本无放大,反应谱比最大值的均值小于1.1。
(3)盆地边缘区域的放大系数对输入波最为敏感,不同地震波输入下该区域的放大系数在较大范围内变化,同时不同地震波输入下盆地相比一维土层的附加放大特征也存在明显差异,因此盆地场地的地震动放大系数估计中需考虑地震动输入的随机性,给出统计意义上的盆地放大系数。

