基于SSA和双稳随机共振的车削颤振微弱特征提取
吴 飞, 栾天宇, 农皓业
(武汉理工大学 机电工程学院,武汉 430070)
由于车削系统结构刚性限制和切削参数选择不当导致车削稳定性变差,使得颤振在车削加工中时有发生。车削颤振表现为刀具与工件之间剧烈的振动,同时还会伴随噪声的产生,导致车削表面加工质量下降,限制车削加工效率的提升。孙宇昕[1]提出车削颤振存在稳定和颤振两种状态,在二者之间存在过渡阶段,此阶段机床振动的能量开始向一个窄的频带聚集,当颤振已完全发生,机床振动的能量会表现出明显的正弦振动特征,导致时域振动信号的规则性增加。在车削颤振监测中,一般采取的策略是采集颤振时的信号进行(时)频域方法,从频谱中找到颤振特征频率。然而,车削颤振过渡阶段特征非常微弱,加之噪声和转频的影响,频谱中难确认颤振的发展阶段,在量化颤振方面更是难上加难。
自从Benzi等[2]在研究古气象冰川问题提出随机共振理论以来,随机共振技术进一步促进了提取信号中微弱特征技术的发展和应用。王慧等[3-5]通过噪声、输入信号以及非线性系统之间的协同配合,噪声能量逐步向微弱信号频率处聚集,使得原本微弱的特征信号能够被清晰地辨识,实现对微弱特征信号的检测。
为了使随机共振应用于实际的机械故障检测中,研究人员利用变尺度[6-8]、移频变尺度[9]、归一化[10]等方法突破绝热近似理论的小参数限制,实现对高频微弱特征信号的提取。王衡为突破绝热近似理论的小参数限制,利用二次采样技术将频率压缩尺度R引入,并作为二阶随机共振系统参数进行寻优。
为了增强微弱信号提取中的随机共振现象,研究人员通过优化随机共振系统结构[11-13]和提高智能优化算法的寻优效率,获得更高的输出信噪比。经哲等[14]将量子遗传算法(genetic quantum algorithm, QGA)对传统随机共振系统参数进行优化,实现对液压泵故障振动信号的降噪预处理;高康平等[15]利用麻雀优化算法(sparrow search algorithm,SSA)寻优能力强、收敛速度快的特点,结果表明相较于PSO-SR模型,SSA-SR具有更强的优越性与实用性;李国英等[16]考虑到不同带限噪声对特征信号的提取效果,在经典二阶随机共振系统基础上引入Paul小波实现对不同频带噪声强度的控制,提升了随机共振系统检测效果。另外,由于以信噪比作为调整随机共振系统参数的评价指标时需要预知准确的故障频率,这在实际的故障特征提取场景中很难实现。曹衍龙等[17]结合峭度和近似熵构建冲击特征系数结合随机共振提取冲击信号。王俊等[18]提出加权功率谱峭度(weighted power spectral kurtosis,WPSK)来代替信噪比作为衡量随机共振系统优化指标,摆脱对先验知识的依赖,但实际应用仍有诸多限制。
针对上述问题,本论文的研究工作就是基于随机共振理论,以信噪比为评价指标,利用麻雀优化算法算法选取最优双稳态随机共振(bistable stochastic resonance, BSR)系统参数,即SSA-BSR模型,以此增强并提取微弱的车削颤振过渡阶段状态特征,提高车削颤振识别和监测的有效性和准确性。仿真信号和车削颤振试验数据分析表明,该方法能有效、准确地实现车削颤振过渡阶段微弱特征的识别与诊断,为实际工程应用提供一种新思路。
1 理论背景
1.1 二阶双稳态随机共振模型
随机共振由周期信号、噪声和非线性系统共同作用产生,二阶双稳态随机共振模型如式(1)所示
(1)
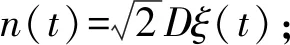
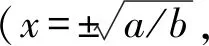
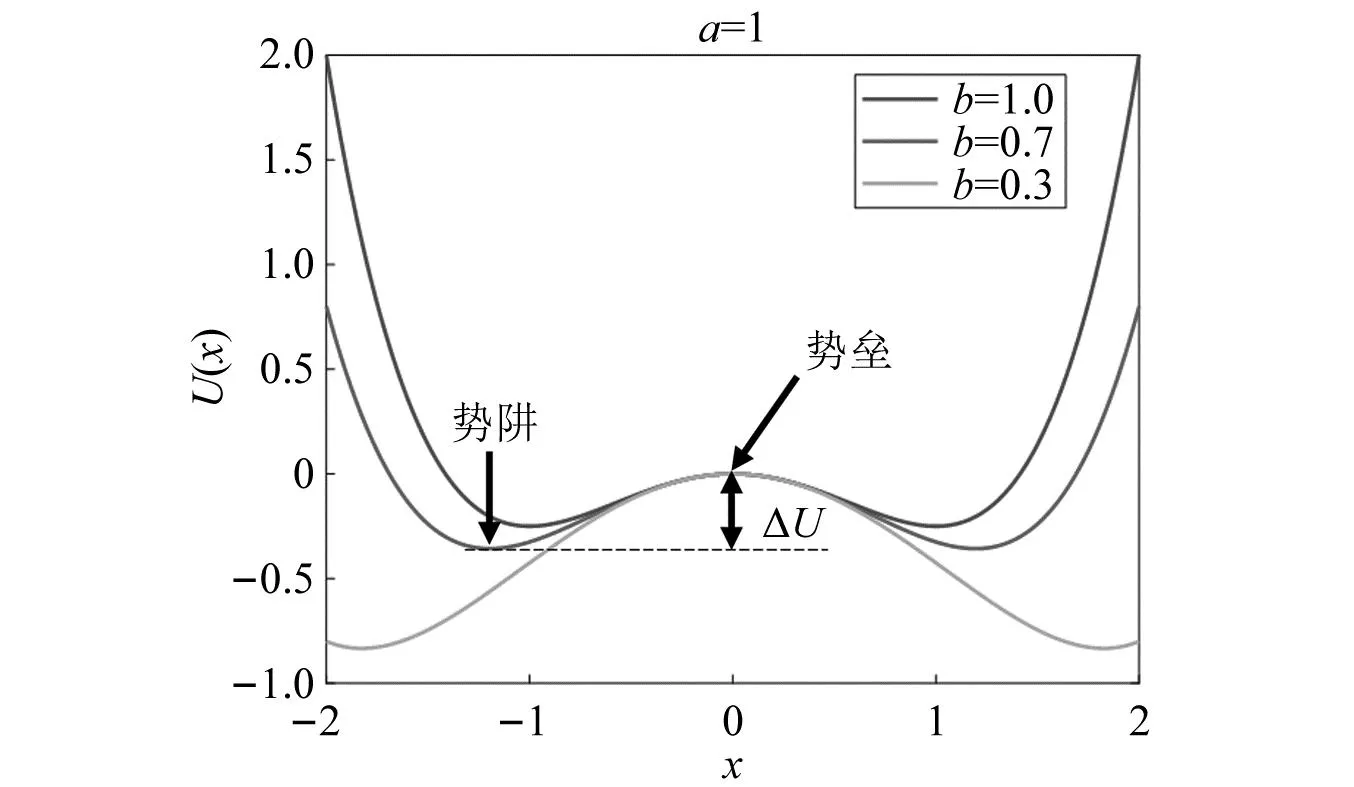
图1 不同形状的双稳态势阱
对于式可由四阶龙格库塔方程求解,具体求解过程为
(2)
(3)
式中:S(n)为含噪声的随机共振系统输入信号;xn为随机共振系统的输出信号;h为数值计算步长。
王衡研究了阻尼比k、噪声强度D对随机共振系统的影响规律,噪声强度对随机系统有一定的影响,但实际应用中噪声无法控制。因此,系统参数a、b以及阻尼比k是影响随机共振模型性能的主要因素,同时考虑到实际车削颤振故障频率远大于1 Hz,采用二次采样技术引入频率压缩尺度R。如何通过对参数a,b,k,R的选定使系统输出处于最优随机共振状态是本文接下来要解决的问题
1.2 麻雀搜索算法
麻雀搜索算法是Xue等[19]依据麻雀种群行为提出的一种群体优化算法,可以同时优化SSR模型的四个系统参数,具有优秀的寻优能力和收敛速度。算法[20]通过计算初始种群适应度值并进行排序,对发现者、加入者及预警者的位置进行更新,再利用对比迭代得到全局最优解。SSA基本理论如下:
通过n只麻雀组成种群寻找最优解,种群由集合(Xi,fi)表示,Xi表示麻雀所处的位置,即带求解中的变量;fi=f(Xi),表示每个个体的适应度值。种群与种群适应度分别如式(4)、式(5)所示
(4)
(5)
式中:d为待求解变量维度;f为适应度函数。
在优化过程中,发现者位置更新如式(6)所示。
(6)

加入者位置更新如式(7)所示
(7)
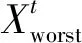
预警者位置更新如式(8)所示
(8)

SSA算法的主要思想是基于麻雀种群内部的分工和社会互动,算法通过发现者的搜索机制广泛地探索解空间,通过加入者在发现者范围搜索来达到局部搜索,这两者平衡了算法的探索与开发,接着通过预警机制,防止算法陷入局部最优。
1.3 适应度函数
信噪比(signal-to-noise ratio,SNR)用作SSA算法的适应度函数。SNR是用来评价微弱信号的常用指标之一,当SNR越大,说明信号的噪声干扰越少,信号越纯净。本文以SNR作为基于SSA的BSR检测微弱信号的评价指标,其具体计算如下:
对一组离散信号x={x1,x2,…,xN},N为信号的长度。对信号x进行快速傅里叶变换得到频率序列X(k)和幅值序列Y(k),可表示为
(9)
设信号频率f0处的谱峰值序号为K0,可由式(10)求得
(10)
式中,fs为信号的采样频率,由此可得信号SNR为
(11)
经前期试验测试发现,车削加速度振动信号信噪比均大于-50 dB,存在由于不合适的系统参数导致输出信号完全失真,使得输出信噪比为空的情形;同时信噪比均为负值且SNR值越大fs信号特征越明显。系统参数优化的目标是寻找最小值问题,以及保证算法正常运行,故构造适应度函数f(X)如下
(12)
采用适应度f(X)函数值对以系统参数a、b,阻尼比k,频率压缩尺度R作为系统参数的随机共振系统的输出信号进行评价。当适应度f(X)函数值最大时,得到最优系统参数组合,输出信号为最优的滤波信号。
1.4 基于SSA-BSR的车削颤振微弱特征提取方法
基于上述讨论,以信噪比作为双稳随机共振系统(BSR)输出信号的评价指标,利用麻雀搜索算法自适应选取BSR系统参数a,b,k,R,将最优参数组合输入至BSR系统,进行频谱分析,提取微弱信号特征。
下面为基于SSA-BSR模型的车削颤振微弱特征提取的具体步骤:
步骤1获取车削颤振振动信号;
步骤2数据预处理。对原始信号而言,时域信号记为S0,S=S0-mean(S0),去除原始信号中的直流分量,将S作为随机共振系统的输入信号;
步骤3初始化参数和总群。初始化SSA算法参数,设置参数a,b,k,R的寻优范围,即a∈[0.01,5],b∈[0.01,10],k∈[0,1],R∈[200,2 000],随机生成初始总群X,种群每个个体由a,b,k,R四维变量组成。

步骤5麻雀位置更新。将种群中个体按适应度从小到大进行排序,取前20%数量的麻雀作为发现者,按式(6)更新,其余麻雀作为加入者按式(7)更新,再计算更新后的各个体适应度值。选取若干个体作为预警者,按式(9)进行更新,并计算适应度值;

步骤7更新迭代次数,以是否达到最大迭代次数作为循环结束的判据。如果小于最大迭代次数返回步骤四继续计算,否则跳出循环执行步骤八;
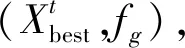
基于SSA-BSR的车削颤振微弱特征提取流程如图2所示。
2 基于SSA-BSR的微弱特征提取仿真分析
本文利用二次采样技术引入频率压缩尺度R,将微弱信号特征信号检测问题转化为二阶稳态随机共振系统a,b,k,R四个参数的同步优化问题,使用SSA算法快速、准确寻找出BSR系统的最优参数,处理强噪声背景下含微弱周期特征的仿真信号,完成微弱周期信号的提取,验证提出方法的可行性。
输入含噪信号为S(t)=A0sin(2πf0)+n(t),其中A0为0.21,f0为300 Hz,n(t)为高斯白噪声,噪声强度为1.5,采样率为2 kHz,采样点数为4 000,其时域波形和幅值谱图如图3所示,依据式(11)求得初始信号信噪比为-27.35 dB,信噪比非常低,时域波形中很难观察出信号的周期性,幅值谱中可以辨别出300 Hz周期信号的幅值为0.18,但整个频段中充满噪声干扰。
如图4所示,利用传统随机共振方法处理原始仿真信号,信号中的周期成分的得到提取和增强,高频段噪声被抑制,但目标特征并未被捕捉。
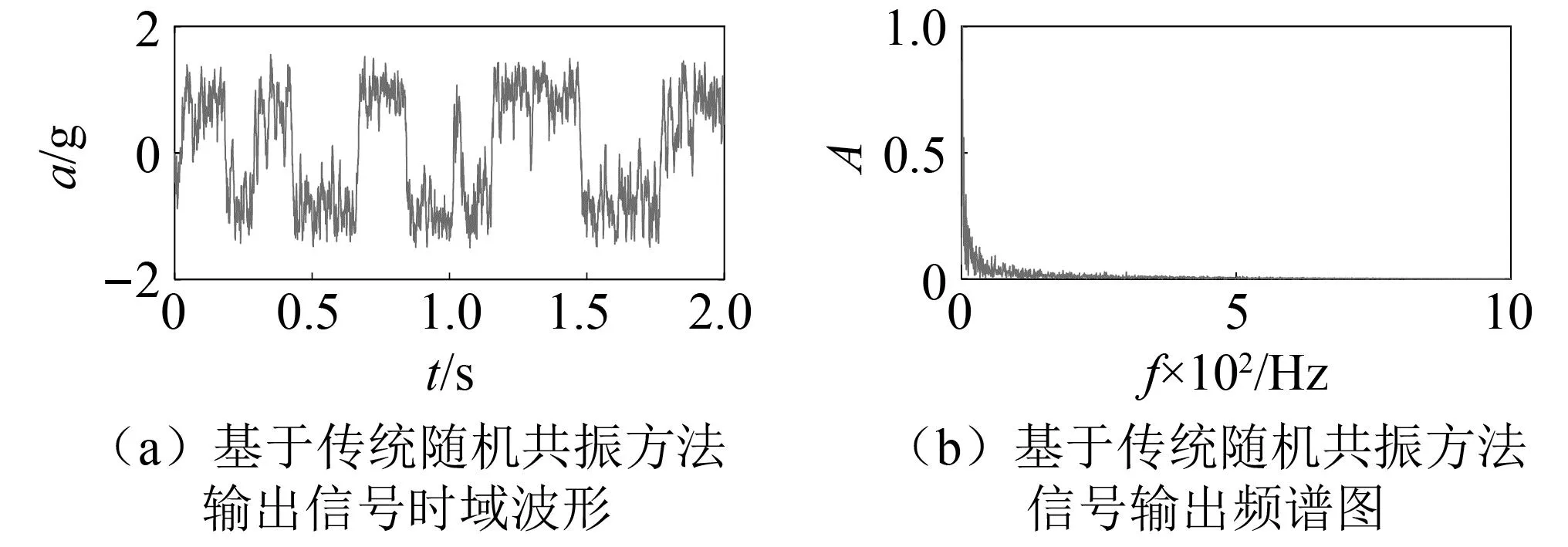
图4 传统随机共振方法
分别利用基于遗传算法的双稳随机共振(GA-BSR)方法、基于双链量子遗传算法的双稳随机共振(DCQGA-BSR)方法以及基于麻雀搜索算法的双稳随机共振(SSA-BSR)方法对原始信号进行处理,对比信号输出结果。其中,总群数量为20,最大迭代次数为50,a∈[0.01,5],b∈[0.01,10],k∈[0,1],R∈[200,2 000];GA-BSR方法中交叉概率0.9,变异概率0.2;DCQGA-BSR方法中,转角步长0.01π,变异概率0.05;SSA-BSR方法中安全阈值0.8,发现者所占比例为20%,预警者数量为10。不同方法处理后振动信号时频波形对比如图5所示。
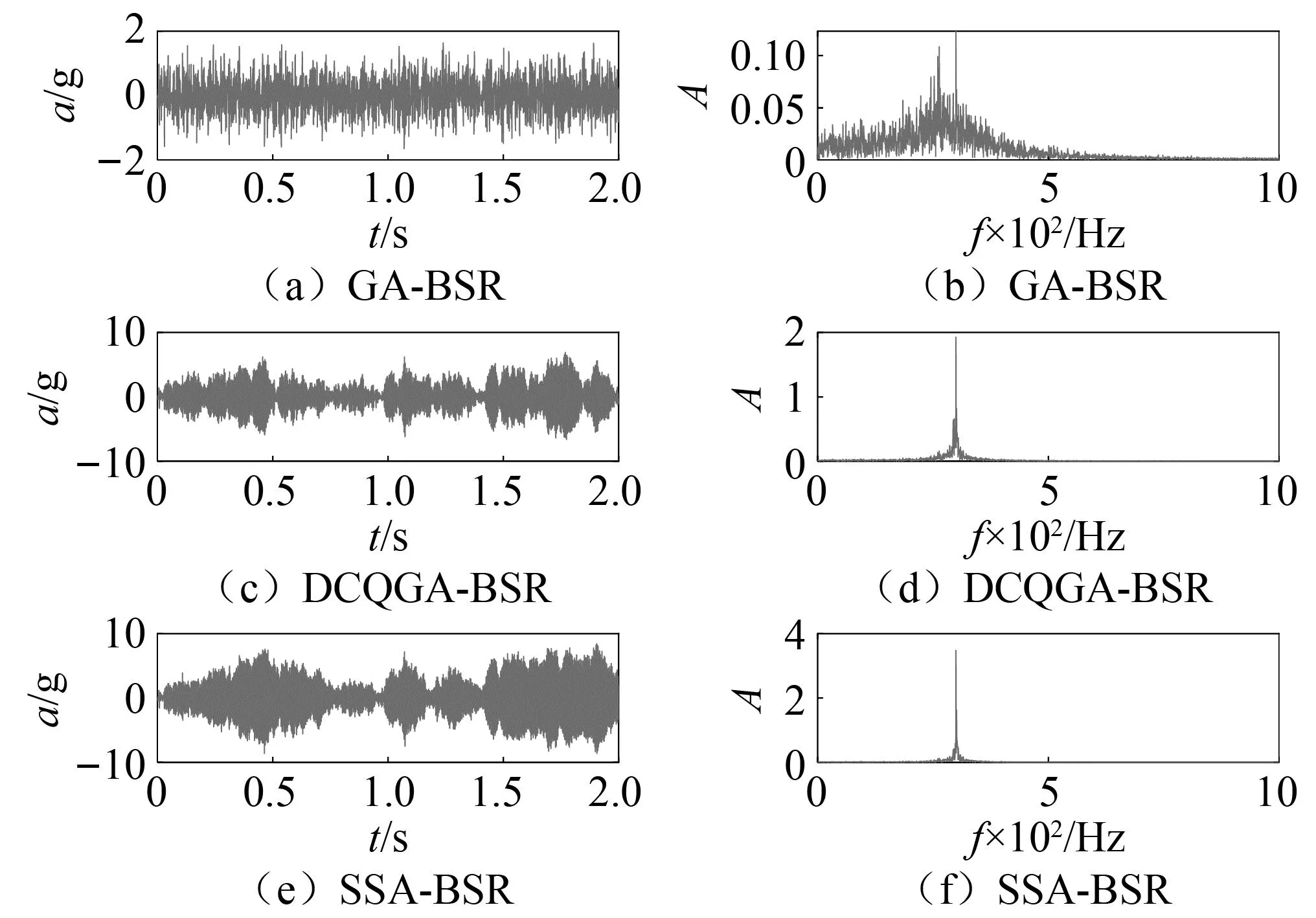
图5 不同方法处理后仿真信号时频波形
从信号处理效果进行分析,GA-BSR方法输出结果输出如图5(a)、图5(b)所示,尽管信噪比得到提高,但仍存在明显的中低频干扰,特征频率附近的噪声成分抑制不明显,特征频率幅值为0.123;DCQGA-BSR方法输出结果如图5(c)、图5(d)所示,时域波形图中信号规则性增加,周期成分更加明显。从幅值谱中可以看出DCQGA-BSR方法明显抑制了噪声对特征信号的影响,同时特征频率幅值增强至原始信号的10倍,实现对微弱特征信号的提取与增强;SSA-BSR方法输出结果如图5(e)、图5(f)所示,较于DCQGA-BSR方法,输出信噪比进一步提高,特征信号幅值的增强至原始信号的20倍,较DCQGA-BSR方法有更明显的提升效果。
寻优过程及输出结果分别如图6和表1所示。从算法运行效率进行分析,相较于DCQGA方法在48次迭代后寻找到最优参数,利用SSA方法选取BSR系统最优参数可以在10次迭代以内到达收敛,同时输出信号具有更高的信噪比,进一步加快优化进程,提高探索全局最优解的概率。

表1 不同方法计算结果
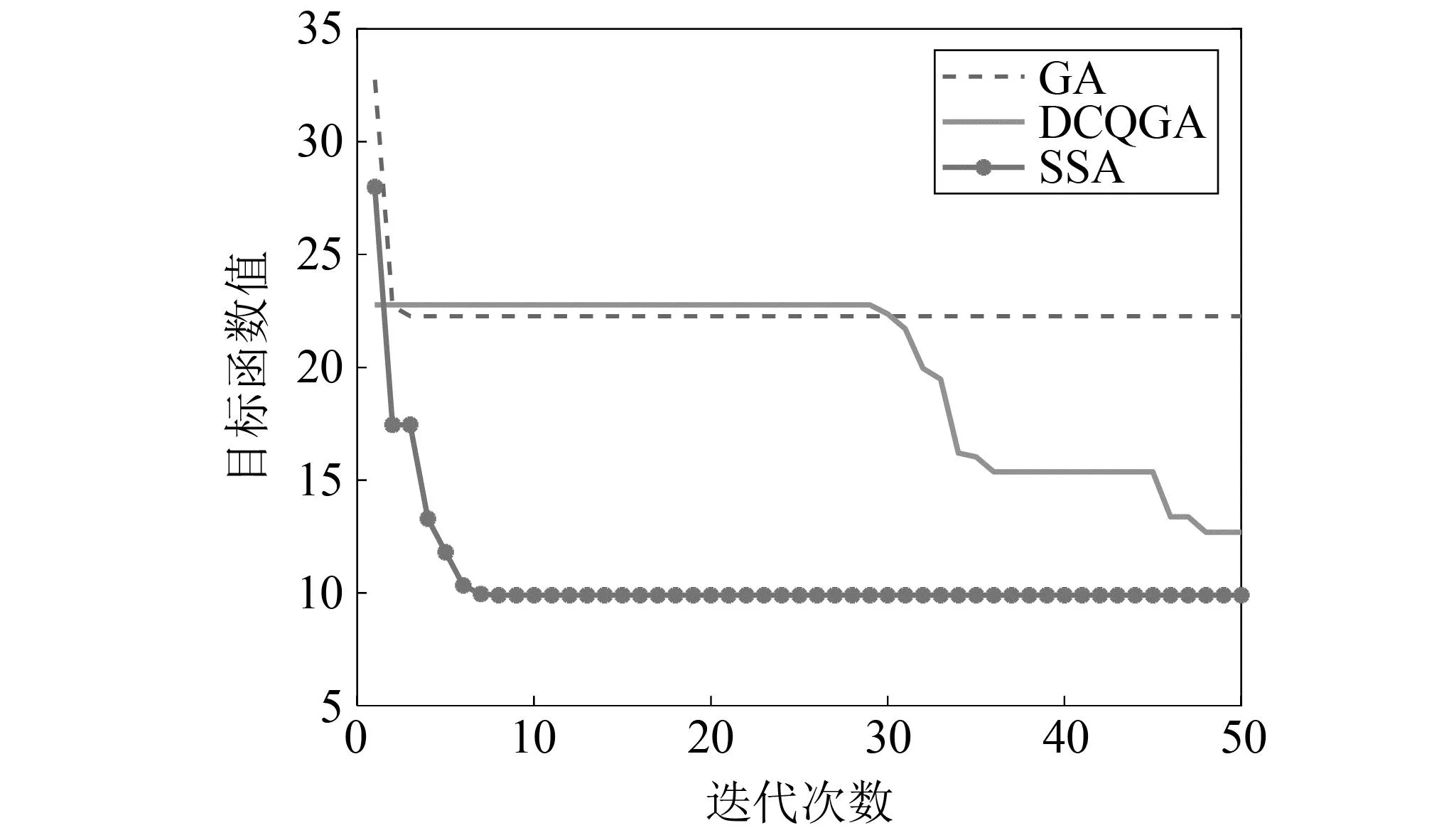
图6 不同方法对仿真信号的寻优过程
因此,SSA-BSR方法可以实现对强噪声背景下微弱特征信号的提取与增强,同时兼顾寻优速度快和获得全局最优解概率高的优点。
3 车削颤振实测信号试验
车削颤振的激发过程中存在过渡阶段,该阶段特征特征频率能量微弱,若是在过渡阶段将车削颤振辨识出来能够有效降低车削颤振对加工表面的影响。因此,为了进一步验证本文所提方法的实用性和有效性,本节详细地介绍SSA-BSR方法在车削加工中的实施过程。
车削颤振检测试验台布置如图7所示,采用SK50P数控卧式车床,刀具采用93度三角外圆车刀杆和TNMG160404R-S金属陶瓷刀粒。356A15三向压电式加速度传感器加装磁力表座后吸附在刀柄处,并通过BNC电缆与NI数据采集卡上的采集通道连接,实现加工过程中振动信号的实时采集,采样频率为2 133 Hz,车削试验加工参数如表2所示。

表2 车削试验加工参数

图7 车削颤振试验系统组成
再生颤振最终会使工件表面出现肉眼可见的波状振纹,从结果上来看颤振将显著影响工件的表面波纹度。结合表面粗糙度波动程度和外圆车削的一般精度,根据加工后工件表面粗糙度以及表面振纹情况,将加工阶段分为稳定加工阶段、过渡加工阶段、剧烈加工阶段。设置如表所示的工艺参数组合对20MnCrS5棒料开展外圆切削加工试验,以获取经过稳定、过渡和颤振的振动信号,图8为加工后棒料外表面,其中图6截取了试验过程中部分Z方向加速度信号时频波形。

图8 车削加工表面
车削颤振激发过程如图9所示。图9(a)为颤振激发过程域信号图谱,从颤振特征提取角度来看稳定加工阶段与过渡加工阶段之间区别并不明显,剧烈颤振阶段较于两者非线性成分增加,信号边缘出现不平稳波纹。图9(b)、图9(d)、图9(f)分别为7.97 s、9.75 s、10.32 s处窗长为1 000的时域信号图。图9(c)、图9(e)、图9(g)为上述时间段时域图对应的功率谱图,从中可以看出随着颤振程度的加深信号能量逐渐向颤振频率(315.39 Hz)处聚集。图9(h)表示在颤振激发过程中颤振频率幅值的变化趋势,其中步长为100,窗长为1 000。其中,0~8.90 s处于稳定加工阶段,颤振成分并未出现,属于正常加工阶段,仍然能获得光亮的加工表面;8.90~10.01 s处于过渡阶段,由于再生颤振效应,颤振频率能量开始逐渐积累,信号幅值缓慢增大,加工表面出现细微振纹;在10.01 s附近颤振频率成为频谱峰值频率,加工表面随着颤振能量的增强而出现剧烈的振纹。
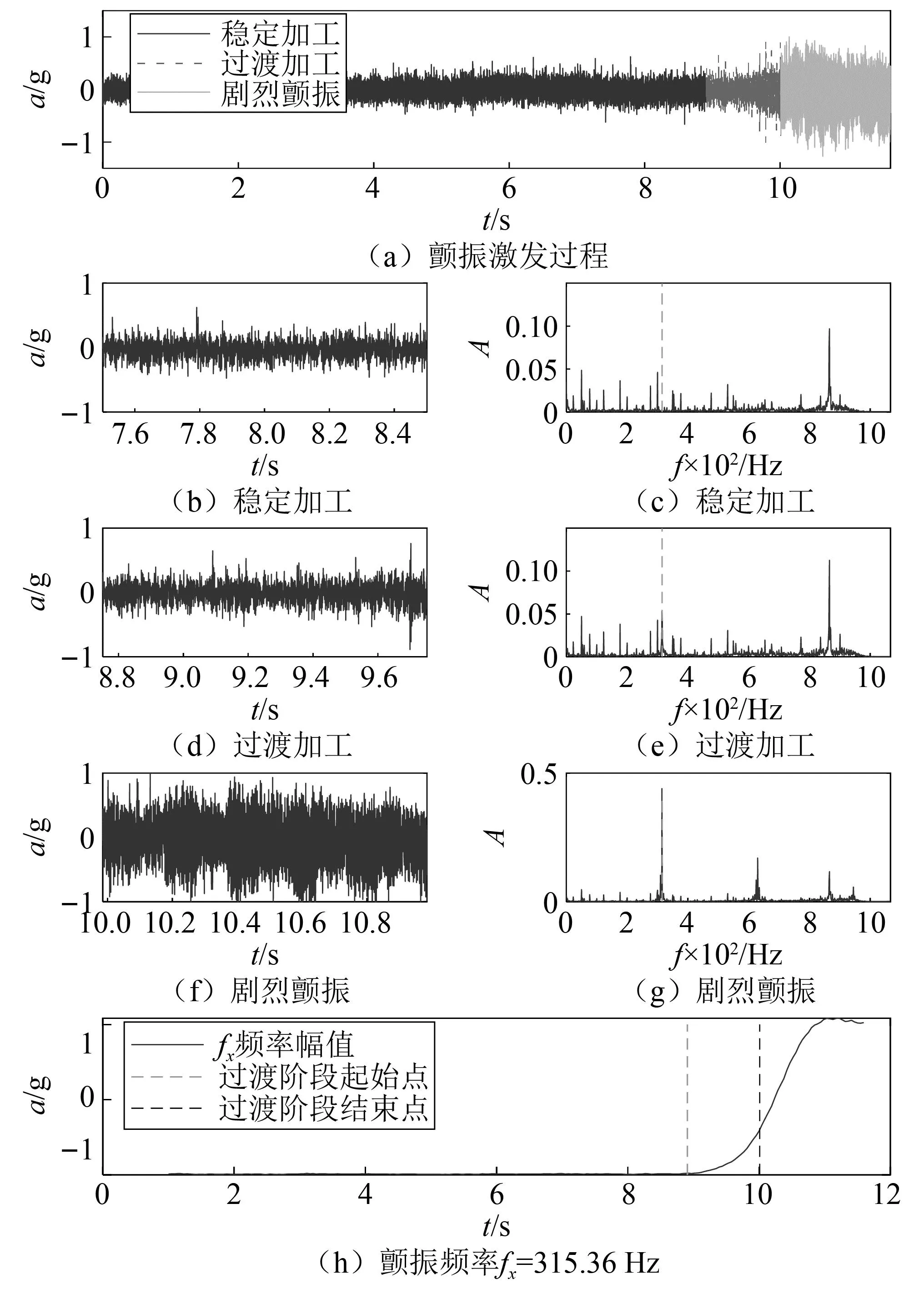
图9 车削颤振激发过程
基于以上现象和分析,可以得出车削颤振的发生导致颤振频率的出现,而车削颤振的剧烈程度与颤振频率功率谱幅值之间存在强相关性。因此,若能在过渡阶段识别到微弱、缓慢增加的颤振频率并发出预警,可以避免颤振发展进入剧烈阶段,从而消除由于剧烈颤振而导致加工表面的损伤。
图10(a)、图10(b)为t=9 s,窗长为1 000的信号时频图谱。此时处于过渡加工阶段初期,颤振频率非常微弱,颤振频率处幅值仅为0.01,且信号图谱中存在大量噪声、转频及其倍频干扰。图10(c)、图10(d)是GA-BSR方法的输出结果,高频干扰已经完全滤除,低频干扰也得到了一定程度抑制,但仍无法探测出明显的颤振频率。图10(e)、图10(f)为DCQGA-BSR方法的输出结果,可以看出明显的周期成分,颤振频率幅值相较于原始信号得到明显提高;图10(g)、图10(h)为SSA-BSR方法的输出结果,与DCQGA-BSR方法输出结果相似,颤振频率得幅值得到进一步提高。
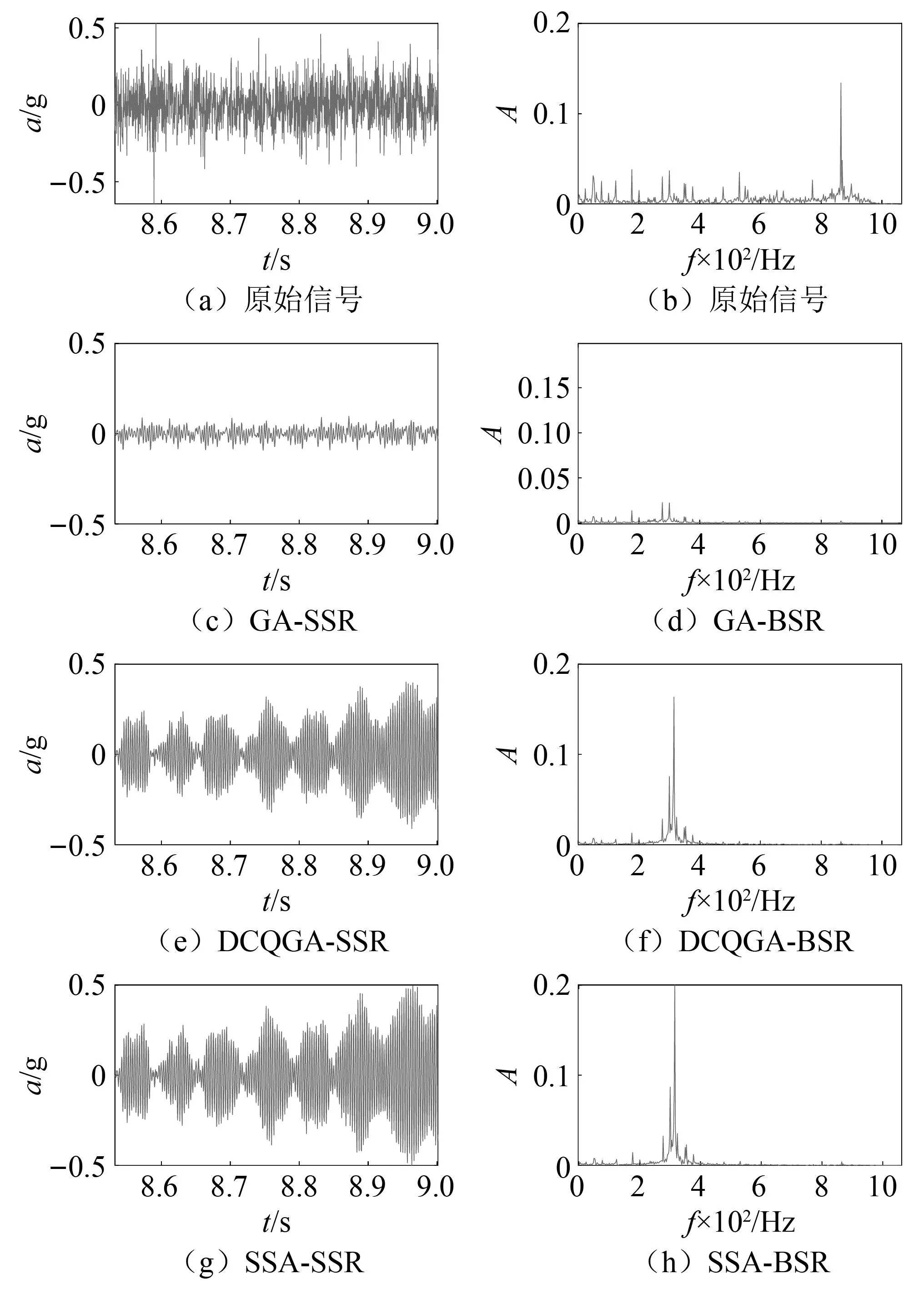
图10 不同方法处理后过渡阶段信号时频波形
考虑到颤振过渡阶段发展迅速,实际应用过程中对算法的寻优效率具有一定要求,图11为上述试验中t=9 s时三种算法运行30次后的平均效率对比图,目标函数值为信噪比的负值。在过渡阶段初期,颤振频率微弱被干扰频率淹没时,SSA算法可以在10次迭代以内寻找出最优参数组合,相对于DCQGA和GA算法具有更高的种群遍历能力和更快的寻优效率。
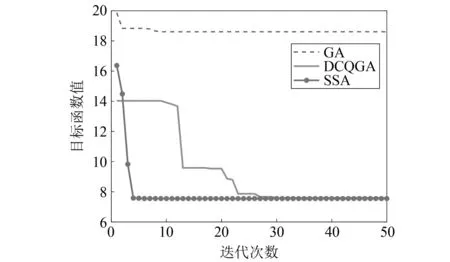
图11 不同方法处理后过渡阶段信号时频波形
为有效避免剧烈颤振阶段对加工表面造成的损伤,需要在过渡阶段内将颤振频率辨识。保持SSA-BSR方法其他参数不变,将最大迭代次数设为10,SSA中预警者数量为4,不同窗长的SSA-BSR方法测试结果如表3所示,其中时间t和SNR为每类窗长SSA运行10次的运行平均值。
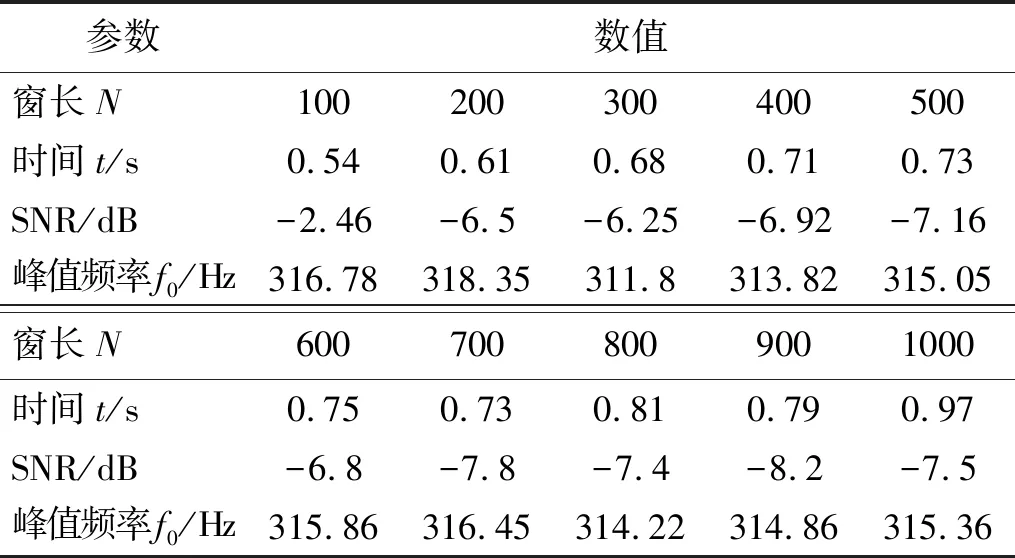
表3 不同窗长的SSA-BSR模型运行效率对比
不同窗长导致不同的频率分辨率,检测出的峰值频率也会不同。为兼顾检测效率与检测精度,实际检测过程中选择窗长为500,10次平均检测时间为0.73 s,能够在过渡阶段在10.01 s结束前完成颤振频率的识别,满足在进入剧烈颤振前识别出颤振频率的要求。
综上,实际车削颤振检测试验验证了本文提出方法在提取微弱信号特征的优越性与实用性,为实现车削颤振过渡阶段的在线监测奠定基础。
4 结 论
针对车削颤振激发过程中存在过渡阶段,颤振频率幅值与颤振的发展阶段存在强相关性,过渡阶段中颤振频率幅值微弱,本文提出SSA-BSR模型。通过开展仿真和实际车削颤振检测试验,消除、抑制其他干扰频率,增强颤振频率特征,提高颤振频率识别的敏感性,实现在过渡阶段初期探测出颤振频率,并能够在进入剧烈颤振阶段前发出预警,由此避免因进入剧烈颤振阶段造成的加工损伤,验证了本文所提方法的优越性和实用性,为车削颤振监测提供了一种新思路。
后续研究在车削颤振机理分析的基础上,结合深度学习对预处理后频谱的关键特征信息进行深层次挖掘,进一步实现对车削颤振的量化,从而进一步实现车削颤振精准、快速诊断。

