风向角对高速列车驶出隧道过程中气动效应的影响
王磊,李宇杰,张传凯,骆建军,叶子剑
(1.北京交通大学 土木建筑工程学院,北京,100044;2.北京市地铁运营有限公司,北京,100044;3.北京地铁工程管理有限公司,北京,100005;4.中国地质大学(北京) 工程技术学院,北京,100083)
侧风条件下高速列车的运行安全性一直是近年来的研究热点[1-3]。除列车自身因素外,基础设施类型对列车气动特性也会产生影响[4]。随着我国高速铁路建设向西部山区拓展延伸,铁路会穿过不同的线路类型,导致列车气动特性发生突变[5],可能危及列车运行安全。
国内外众多学者已经对横风条件下高速列车通过隧道时的气动效应开展了系列研究。一方面,在隧道气动效应研究方面,骆建军等[6-8]进行了横风条件下高速列车驶入隧道过程的数值模拟研究,分析了隧道外横风对隧道内气动压力、列车风风速的影响;邓锷等[9]与WANG等[10]分别研究了横风下高速列车驶入和驶出隧道过程中列车周围的流场分布特性;ZHOU等[11]采用非定常湍流模型针对侧风风向与列车运行方向平行情形,深入分析了列车驶入过程中隧道内压力波变化规律,发现列车逆风向运行时隧道内压力波变化幅值增大。另一方面,在高速列车通过隧道时列车气动特性方面,LIU等[12]对兰新高铁典型路段进行了现场实车试验,分析了强风对列车气动特性的影响;DORIGATTI等[13-14]采用模型试验研究了横风条件列车运行状态下列车表面的压力分布;苗秀娟等[15-16]采用数值模拟手段分析了高速列车驶出隧道遭遇横风时的瞬态气动特性,发现头车发生事故的风险最高;LUO等[17-18]针对横风下列车突入隧道情形研究了高速列车的气动特性;DENG等[19-20]基于数值方法研究了横风作用对高速列车通过路-隧过渡段时气动荷载的影响;LIU等[21]以风区新疆铁路为研究对象,提出了侧风条件下列车运行安全性的评价方法。
现有研究多以横风条件下隧道气动效应和列车气动特性为研究对象,但在现实中,自然风与列车运行方向存在不同的夹角。风向角对列车周围流场分布影响显著,导致隧道内气动压力、流场及列车气动荷载差异。为全面反映侧风对隧道及列车气动特性的影响,有必要对不同风向角下隧道气动效应和列车气动特性展开深入研究。
基于此,本文作者建立侧风-隧道-列车三维计算模型,通过与动模型试验进行比对,验证数值模拟方法的准确性,针对不同风向角下隧道内气动压力、列车风风速、流场分布和列车气动荷载进行分析,以揭示风向角对隧道内气动效应及列车气动性能的影响,得到影响行车安全的最不利风向角,为提高列车行车安全提供参考。
1 数值模拟
1.1 几何模型
高速列车为复杂细长结构,若以整车为研究对象进行数值计算,计算成本巨大,对计算机配置要求很高。列车中部具有横截面形状不变的特点,气动力趋于稳定[22]。故本文以某型三车编组动车组列车为研究对象,将列车简化为光滑车体,不模拟转向架、风挡等细部结构。列车宽度W=3.38 m,高度H=3.70 m,头车、尾车长度为26.25 m,中车长度为24.50 m,全车长度为77.00 m,横截面积为11.2 m2,如图1所示。隧道采用净空面积为100 m2的高铁单洞双线隧道,净跨为13.20 m,净高为8.78 m,线路间距为5.00 m,如图2所示。隧道长度取500 m,列车通过隧道时阻塞比为0.112。

图1 高速列车模型Fig.1 Model of high-speed train
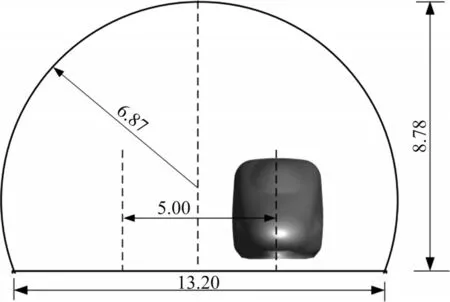
图2 隧道断面示意图Fig.2 Schematic diagram of dimension of tunnel
1.2 边界条件
隧道出口端空气域长为300 m,宽为160 m,隧道中线到迎风侧、背风侧边界面的水平距离分别为40 m和120 m;入口端空气域长、宽均为100 m,高度均为80 m。列车到隧道出口的初始距离为145.83 m,列车速度vtr=97.22 m/s。数值模型的计算域如图3所示。
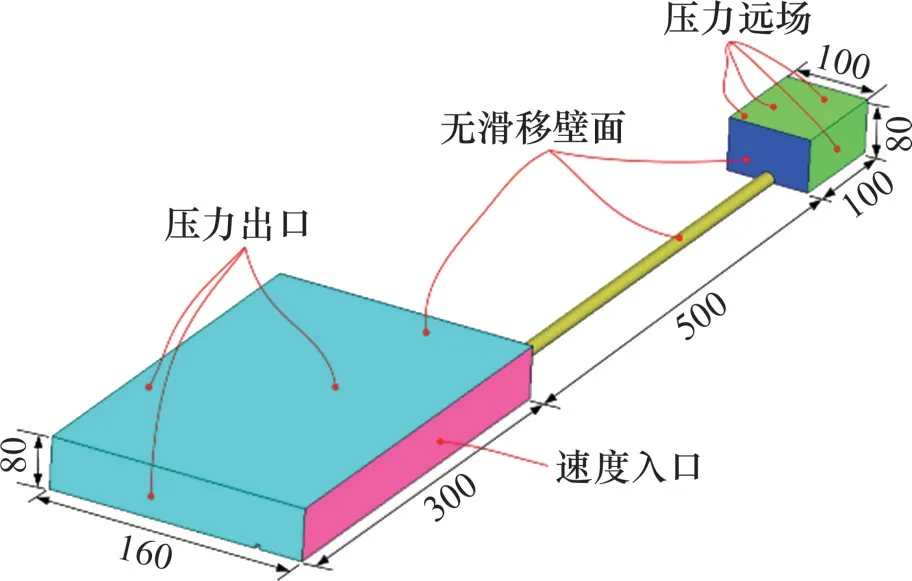
图3 计算域示意图Fig.3 Schematic diagram of computational domain
强风采用均匀速度入口(VELOCITY-INLET)边界条件,风速取30 m/s;出口采用压力出口边界条件,即PRESSURE-OUTLET边界,入口侧边界均采用压力远场边界条件(PRESSURE-FAR FIELD),压力均取101 325 Pa。列车表面、隧道壁面、地表采用非滑移壁面(NO-SLIPING WALL)条件,隧道、列车表面粗糙度高度分别为5 mm[23]和0.045 mm[24]。图3所示为数值模型计算域和边界条件示意图。本文采用滑移网格法模拟列车高速运动。本文风向角β分别取0°、15°、30°、45°、60°和90°,其中0°代表风向与列车平行,但方向相反,90°为风向与列车中线垂直情形。
1.3 网格划分
本文采用六面体网格进行网格划分。为准确捕获列车表面的流动结构,边界层内共布置12层网格,首层网格高度为0.01 mm,对应的量纲一高度y+不超过1,增长率取为1.1,如图4所示。在列车纵向,车头、车尾网格进行加密处理,最大网格长度为0.1 m,中车及隧道纵向的最大网格尺寸为0.5 m。模型离散后共生成1 262万个网格。
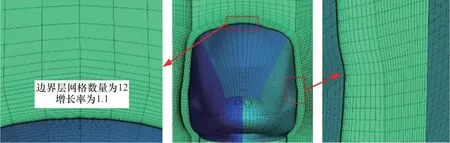
图4 列车表面网格Fig.4 Boundary layer grid on train surface
1.4 测点布置
本文沿隧道纵向设置6个横断面,分别距离出口0、10、20、50、80和110 m,如图5所示。由于隧道洞口处空气动力学效应受横风影响显著,故对出口附近测点进行加密。每个横断面上均设置2个气动压力测点(A、B)和4个列车风风速测点(a~d),测点距离地表2.05 m。

图5 隧道内测点布置Fig.5 Layout of measurement points in tunnel
2 求解策略与数据处理
三维、可压缩、非定常N-S方程通过有限体积法(FVM)离散,压力-速度耦合采用SIMPLE算法,对压力采用迭代法修正。对流-扩散项离散采用二阶迎风格式,时间导数采用一阶隐式方法进行离散。计算时间步长取1×10-3s,每时间步迭代计算20次,湍流项迭代允许残差为10-4。
通常对空气动力学指标进行量纲一化处理,气动压力采用压力系数Cp表示,表达式为
式中:P为计算气动压力;P∞为无穷远处的静压;ρ为空气密度,取1.225 kg/m3;vtr为列车速度,取350 km/h。
作用在列车上的气动横向力、升力是对列车运行安全影响最严重的物理量[25],分别用横向力系数Cy和升力系数Cz表示,两者数学表达式分别如下:
式中:U为气流流速;L、W和H分别为列车长、宽和高;Fy和Fz分别为作用在列车上的气动横向力、升力;Sy和Sz分别为列车沿水平和垂向的投影面积。
3 算法验证
本文采用动模型试验来验证数值模拟的准确性。在模型试验中,高速列车与隧道缩比均为1:8,列车采用三车编组形式,隧道采用单洞复线隧道。列车驶入隧道时的速度为300 km/h,隧道全长为32 m。隧道模型位于半直流风洞试验段内,最大风速为40 m/s,可模拟横风下列车通过隧道情形。试验段长为15.0 m、宽为3.0 m、高为1.5 m,本试验中横风风速为20 m/s。在距离隧道入口5 m、距轨面高度0.471 m处,在隧道壁面对称设置测点A、B以获取列车通过阶段的瞬变压力。
数值模拟中模型尺寸、测点位置均与动模型试验均保持一致。横风风向垂直于列车运动方向,风速为20 m/s,其余边界条件设置与1.2小节相同,网格划分策略与1.3小节相一致。图6所示为测点的气动压力数值结果与模型试验结果对比。由图6可知:测点A、B动模型试验气动压力系数变化规律与数值模拟基本一致,数值结果与动模型试验压力系数变化幅值的相对偏差分别为4.6%和3.3%,均保持在10%以内。由于模型简化导致数值计算结果与模型试验结果之间存在误差,可满足工程要求。故本文数值方法能够真实反映实际情况。
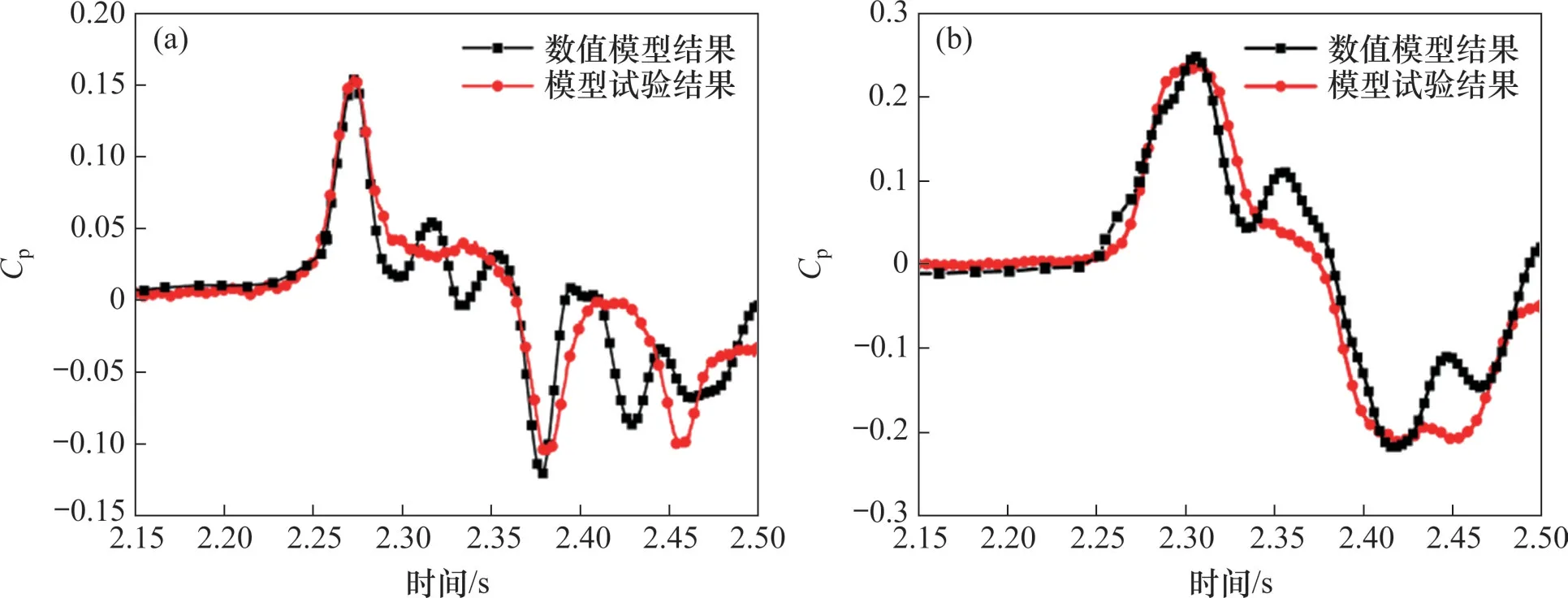
图6 气动压力的动模型试验与数值结果对比Fig.6 Comparisons of moving model test and numerical results of Cp
4 风向角对气动效应影响
4.1 气动压力
图7所示为隧道出口测点压力系数曲线,头车鼻尖与尾车鼻尖驶出隧道的时间为1.500 s和2.292 s,分别对应“H”“T”虚线。由图7可知:不同风向角下列车背风侧压力系数差异较大,受风向角影响更加显著,且列车驶出瞬间差异最为显著,这与列车驶出隧道后复杂尾涡流场结构有关,而列车迎风侧压力系数仅在列车通过阶段差异较大。
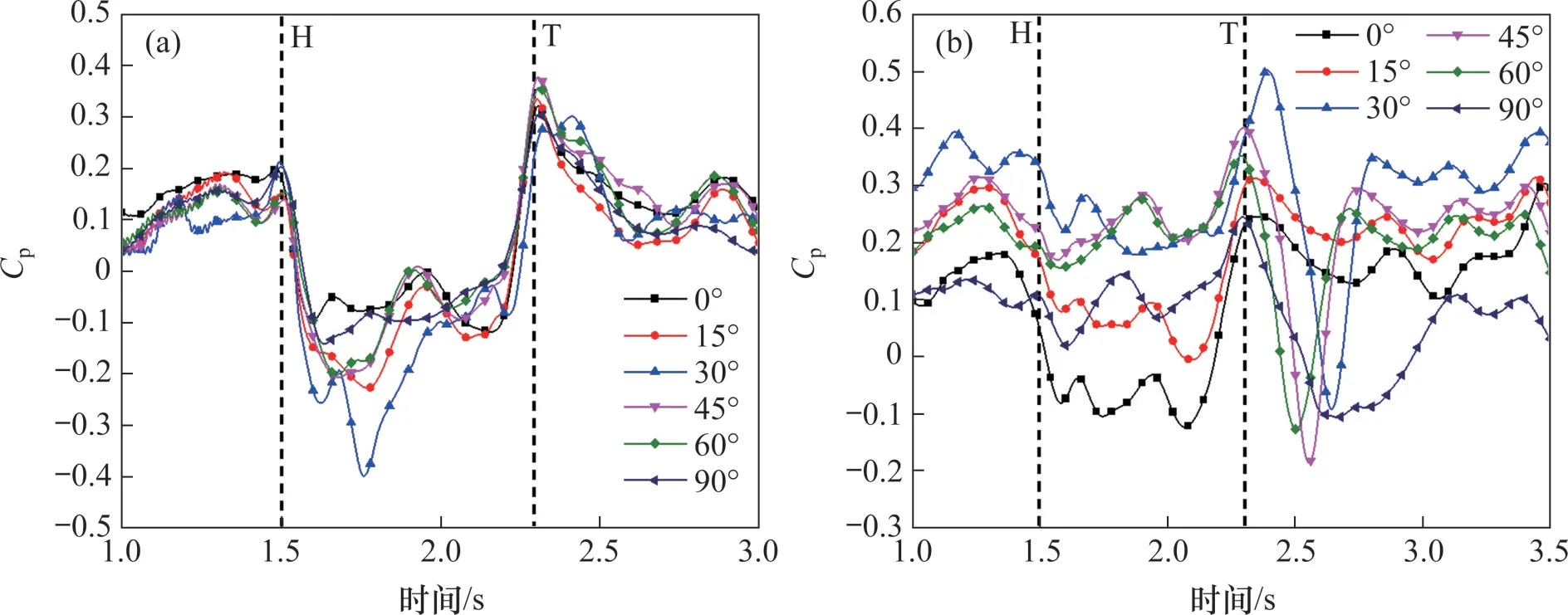
图7 隧道出口气动压力系数时程曲线Fig.7 Time-history curves of aerodynamic pressure coefficient at tunnel exit
此外,当风向角为30°列车驶出时,迎风侧A1测点压力系数变化幅值最大,而背风侧测点B1压力系数在列车完全驶出时压力系数变化幅值最大,前者比后者大20%。
图8所示为出口处测点的压力系数峰值与风向角的关系曲线。由图8可知:迎风侧测点A1的气动压力峰值及其变化幅值变化较大,随风向角增加基本呈现先增大后减小的变化规律,在30°风向角时气动压力变化幅值最大。然而背风侧测点B1压力系数变化幅值随风向角增大呈现先减小后增大再减小的变化规律,并在风向角为15°压力系数峰值最小。
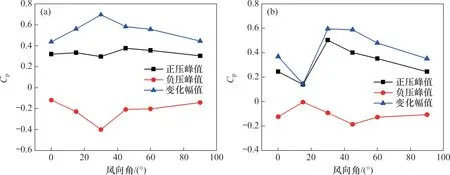
图8 隧道出口气动压力峰值与风向角的关系曲线Fig.8 Relationship curves between pressure peaks and WAs at tunnel exit
图9~10所示分别为距出口10 m、50 m处压力系数峰值与风向角的关系曲线。由图9和图10可知:气动压力系数变化峰值及变化幅值最大值并不是出现在隧道出口,而是到隧道出口一段距离处,变化幅值最大值部位与风向角有关。隧道内相同位置列车两侧隧道壁面压力系数与风向角的变化规律不同,测点A2、B2的正、负压力系数峰值变化规律不同,变化幅值峰值分别对应15°和30°。

图9 距出口10 m处压力系数峰值与风向角的关系曲线Fig.9 Relationship curves between peaks of Cp and WA at 10 m from tunnel exit
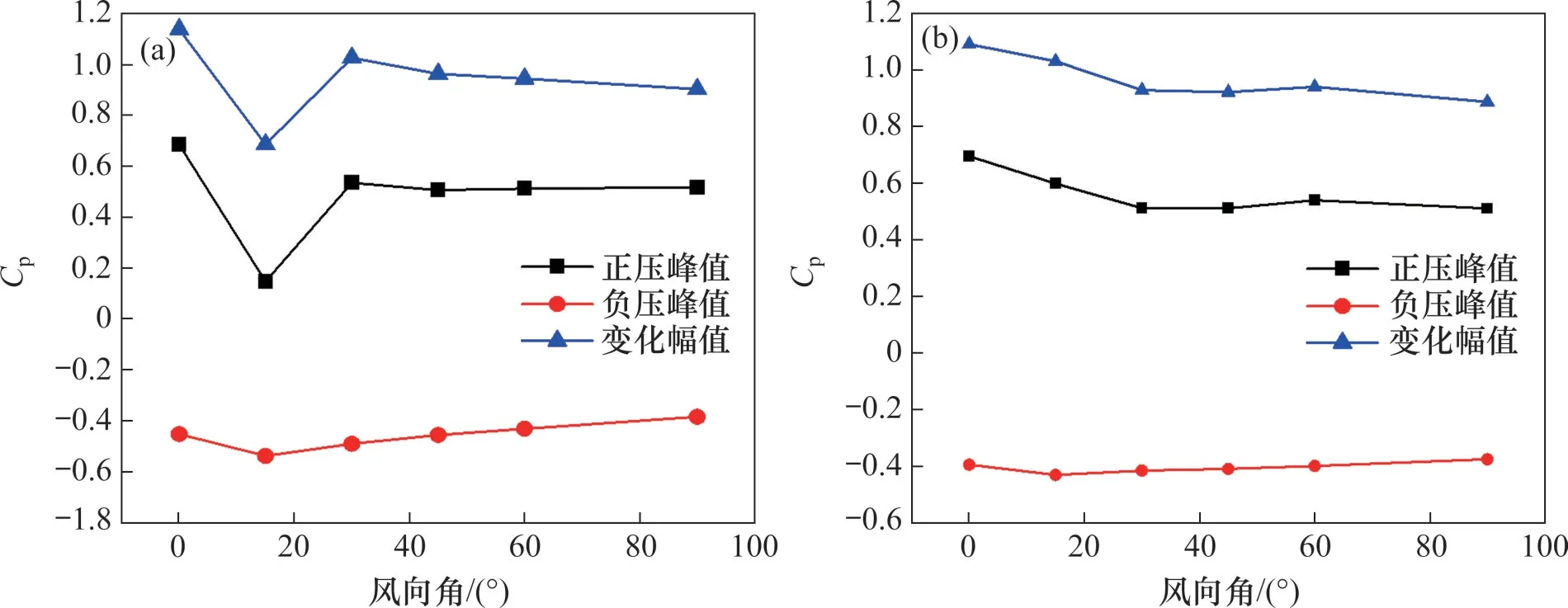
图10 距出口50 m处压力系数峰值与风向角的关系曲线Fig.10 Relationship curves between peaks of Cp and WA at 50 m from tunnel exit
随着到出口距离增大,测点A4、B4正负压力系数和变化幅值随风向角变化规律基本趋于相同。A4测点的压力系数峰值在风向角为15°时最小,测点B4压力系数峰值受风向角影响减弱,在风向与列车运动方向平行时峰值均最大。
4.2 列车风风速
图11所示为隧道出口测点的列车风风速时程曲线。由图11可知:列车迎风侧测点a1的列车风风速在列车驶出瞬间显著增大,且列车风风速峰值随风向角增加呈先增大后减小的趋势,列车风风速峰值为0.92vtr,对应的风向角为30°,见图11(a)。列车背风侧列车风风速波动幅度随着到列车水平距离增大而增大,而列车风风速峰值随到列车距离增大而减小,见图11(b)~11(d)。当风向角为30°时,背风侧b1、c1和d1测点的列车风风速峰值分别为0.99vtr、0.68vtr和0.24vtr。
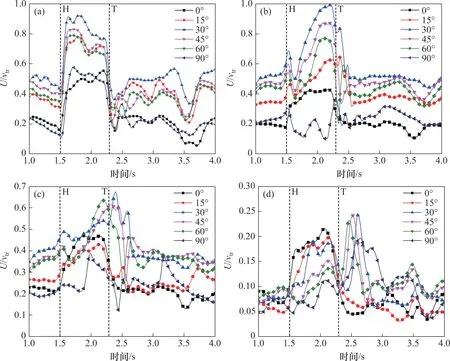
图11 隧道出口列车风风速时程曲线Fig.11 Time-history curves of train wind speed at tunnel exit
与迎风侧测点相似,背风侧列车风风速随风向角增大呈先增大后减小的趋势,当风向角为30°时,背风侧测点列车风风速峰值最大。然而列车两侧列车风风速峰值出现时刻不同,迎风侧测点a1的列车风风速峰值发生在头车驶出时刻,而背风侧列车风风速峰值出现在尾车驶出隧道时刻,且各测点列车风风速峰值时刻随到列车背风侧水平距离增大而延迟,例如当风向角为30°时,背风侧测点b1、c1和d1列车风风速峰值分别出现在2.2、2.4和2.6 s。
图12所示为隧道出口列车风风速峰值与风向角的关系曲线。由图12可知:当风向角β≤30°和β≥60°时,迎风侧列车风风速最大,而风向角β∈(30°,60°)时,列车背风侧列车风风速峰值较大,测点b1的列车风风速峰值最大。无论空间位置如何,当风向角为30°时隧道出口列车风风速峰值最大。此外,背风侧列车风风速峰值随到列车背风面距离增大而显著减小,到列车距离越远,列车风风速受风向角的影响越小。

图12 隧道出口列车风风速峰值-风向角关系曲线Fig.12 Relationship curves between max train wind speeds and wind angles at tunnel exit
图13所示为距隧道出口20 m和50 m处的列车风风速峰值与风向角关系曲线。由图13可知:背风侧列车风风速峰值基本随风向角增大而先增大后减小,而迎风侧列车风风速峰值变化较为复杂,到隧道出口距离不同,变化规律亦不相同。此外,当风向角为30°时,列车风风速峰值最大,但与隧道出口不同的是列车风风速峰值位置发生在距离列车背风面水平4.2 m处,且列车风风速峰值随到入口距离增大而急剧减小。

图13 不同位置列车风风速峰值与风向角的关系曲线Fig.13 Relationship curves of max train wind speeds and wind angles at different positions
4.3 流场分布
图14所示为列车中部驶出隧道时的流场分布图。由图14(a)可知:当风向与列车运行方向平行(β=0°)时,仅沿列车纵向发生流动分离现象,头车鼻尖处压力系数最大,列车背风侧入口存在涡旋,负压最大。隧道内列车两侧空间不同导致迎、背风侧空间流量差异,对称性较差。从图14(b)~(d)可见:一方面,随风向角增大,列车表面正压力系数峰值位置由头车鼻尖逐渐向迎风面偏移,当风向角为90°时,头车顶部负压最大,而当风向角为30°时列车迎风侧隧道入口处负压力系数最大。另一方面,列车表面流动分离程度随风向角增大而增大,在列车背风侧形成起始于头车背风侧的纵向涡旋,流场对称性差。流动分离点到头车鼻尖的距离随风向角增大而呈现先减小后增大的变化规律,风向角为60°时该距离最小。

图14 列车中部驶出隧道时列车周围的流场分布Fig.14 Flow field distributions when train middle exits tunnel under sidewind
此外,随风向角增大,隧道内列车两侧空间内逐渐形成不同尺度的涡旋,流场结构复杂。由此可知,风向角对列车周围流场分布有明显影响,列车绕流具有显著三维特性,列车绕流特性随风向角增大由流线型结构绕流逐渐过渡到钝体绕流。
4.4 气动荷载
图15所示为不同风向角下头车气动荷载时程曲线。由图15可知:当列车由隧道内驶出遭遇强风时,作用在列车上横向力、升力均发生突变,不同风向角导致气动荷载变化规律存在显著差异。当向角为0°时,头车横向力系数Cy变化幅值最小。随风向角增加,列车驶出隧道时头车横向力系数Cy急剧增大,Cy变化幅值呈先增大后减小的变化规律,并且当风向角为30°时,头车Cy变化幅值均最大。与列车驶出阶段不同,当列车完全驶出隧道后,头车Cy随风向角增大而增大并逐渐趋于稳定,当风向角为90°时,头车Cy最大。

图15 头车气动荷载与风向角的关系曲线Fig.15 Relationship curves of aerodynamic loads of HV and WA
由图15(b)可知:当列车驶出隧道时,头车气动升力系数Cz亦发生剧烈波动。当风向角为0°时,头车Cz变化幅值最小。随风向角不断增大,头车Cz波动程度增加,且Cz变化幅值呈现先增大后减小的趋势。当风向角为30°时,头车气动升力变化幅值最大。
图16所示为头车横向力系数Cy、升力系数Cz峰值及变化幅值与风向角的关系曲线。由图16可以看出:当风向角为0°时,头车横向力系数峰值Cy、升力系数峰值Cz及其变化幅值最小。需要注意的是,当风向角为30°时,头车的横向力系数Cy、升力系数Cz变化幅值最大,对应数值分别为0.63和0.32,发生事故风险的概率最大,而不是风向角为90°的情形。
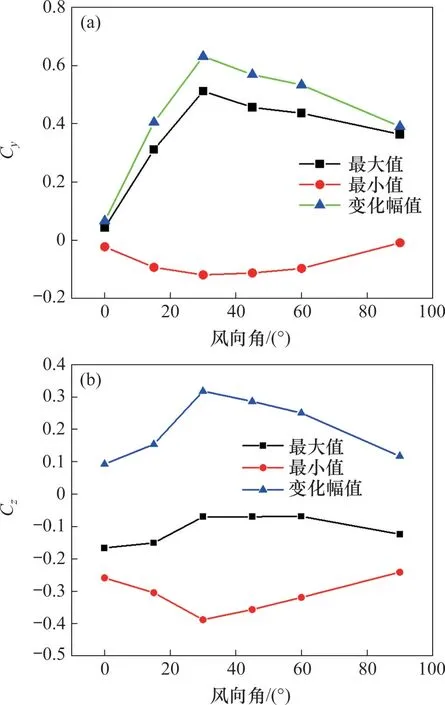
图16 头车气动荷载峰值-风向角关系曲线Fig.16 Relationship curves of aerodynamic load peak of HV and WA
图17所示为中车的气动荷载-风向角关系曲线。由图14和图17可知:中车Cy、Cz峰值与变化幅值随风向角增加而先增大后减小,Cy在60°风向角时变化幅值最大,数值为0.26,Cz在风向角为30°时变化幅值最大,数值为0.28,变化幅值及波动程度远比头车的小。
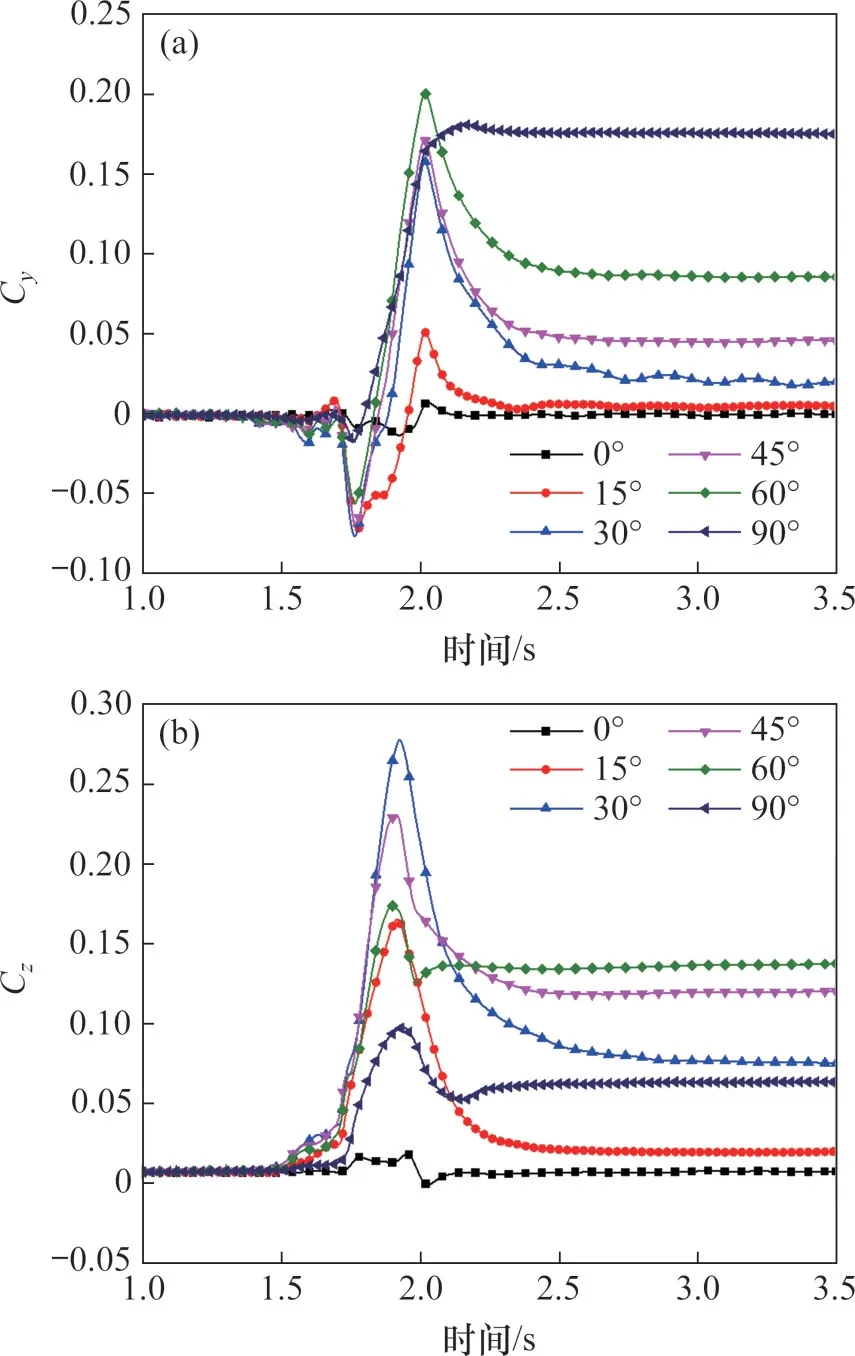
图17 中车气动荷载-风向角关系曲线Fig.17 Relationship curves of aerodynamic loads of MV and WA
图18所示为尾车气动荷载-风向角关系曲线。由图15、17和图18可知:列车驶出隧道时,尾车Cy、Cz波动程度最为显著,它们基本上随风向角增大呈现先增大后减小的趋势,并在30°风向角时横向力系数与Cz变化幅值最大,数值分别为0.24和0.22。列车完全驶出隧道后风向角为0°时尾车横向力、升力波动幅度最大,此时尾车横向摆动最为显著。
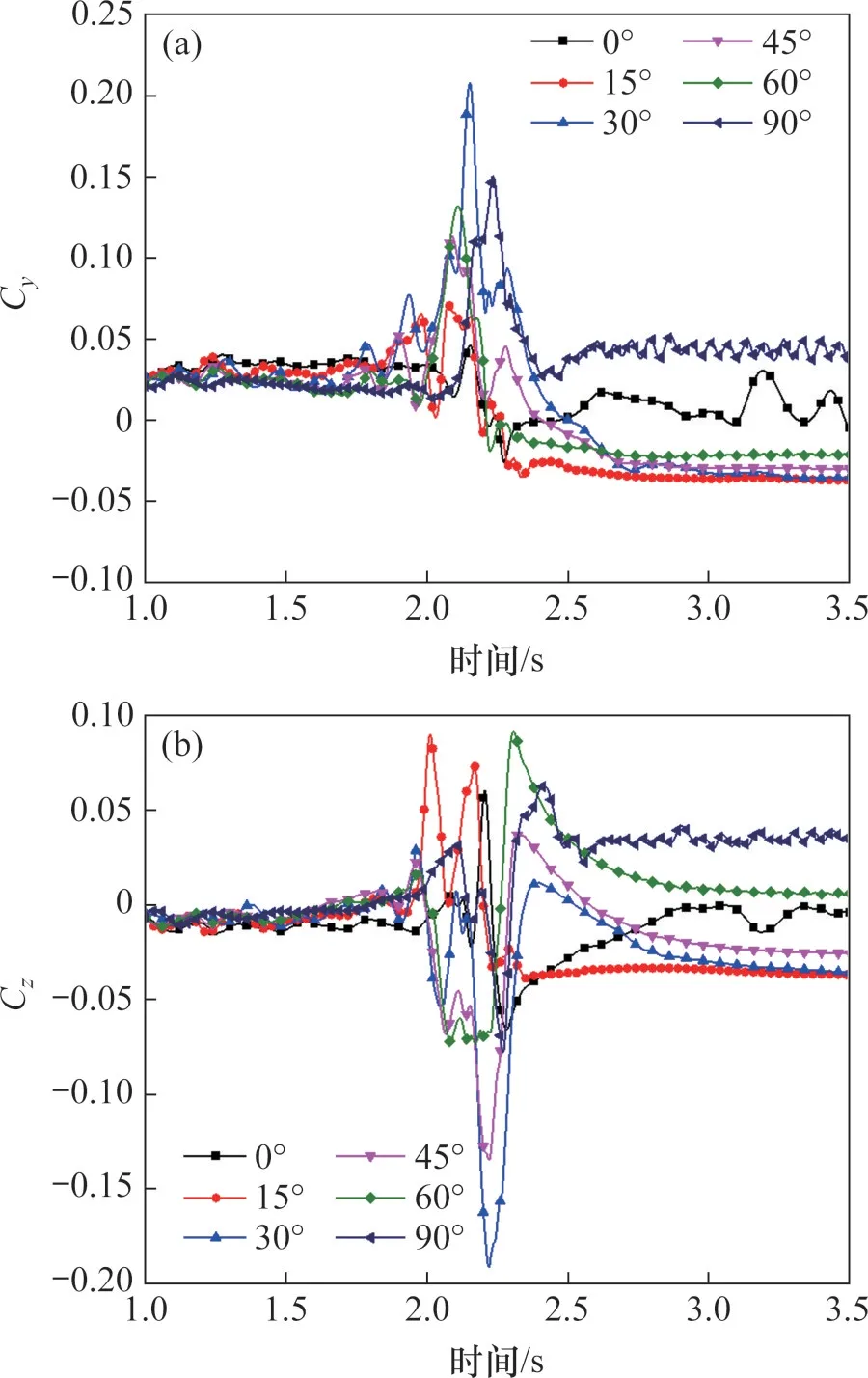
图18 尾车气动荷载-风向角关系曲线Fig.18 Relationship curves of aerodynamic loads of TV and WA
5 结论
1) 隧道出口迎风侧气动压力变化幅值随风向角增大呈现先增后减趋势,背风侧气动压力受风向角影响更大,变化幅值随风向角增大呈现先减小后增大再减小的趋势。此外,隧道壁面气动压力峰值及变化幅值最大值发生在到隧道出口一段距离处,变化幅值最大值部位与风向角有关。
2) 出口处列车风风速随风向角增大基本呈现先增大后减小趋势,30°风向角时列车风风速最大,但迎、背风侧列车风风速峰值分别发生在头车与尾车驶出隧道时刻,且背风侧列车风风速随到列车背风面水平距离增大而急剧减小。
3) 风向角对列车周围流场分布有显著影响。随着风向角增大,流场分布不对称性增强,列车绕流特性由流线型绕流逐渐过渡到钝体绕流,流动分离点到头车鼻尖的距离表现出先增大后减小最后再增大的变化规律,隧道内流动结构愈加复杂。
4) 气动横向力、升力变化幅值随风向角增加呈现先增后减趋势,且头车气动荷载变化幅值最大,其横向力系数最大变化幅值分别是中车、尾车的2.4倍、2.6倍,升力系数最大变化幅值分别是中车、尾车的1.1倍和1.5倍,故保证头车安全是控制整车运行安全的关键。
5) 风向角为30°时,头车气动横向力、升力峰值及变化幅值最大,此时发生列车事故风险最高。

