Outlier-resistant distributed fusion filtering for nonlinear discrete-time singular systems under a dynamic event-triggered scheme∗
Zhibin HU ,Jun HU, ,Cai CHEN ,Hongjian LIU ,Xiaojian YI
1Department of Applied Mathematics, Harbin University of Science and Technology, Harbin 150080, China
2Heilongjiang Provincial Key Laboratory of Optimization Control and Intelligent Analysis for Complex Systems,Harbin University of Science and Technology, Harbin 150080, China
3School of Automation, Harbin University of Science and Technology, Harbin 150080, China
4School of Mathematics and Physics, Anhui Polytechnic University, Wuhu 241000, China
5School of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, China
6Yangtze Delta Region Academy of Beijing Institute of Technology, Jiaxing 314003, China
7Tangshan Research Institute, Beijing Institute of Technology, Tangshan 063099, China
Abstract: This paper investigates the problem of outlier-resistant distributed fusion filtering (DFF) for a class of multi-sensor nonlinear singular systems (MSNSSs) under a dynamic event-triggered scheme (DETS).To relieve the effect of measurement outliers in data transmission,a self-adaptive saturation function is used.Moreover,to further reduce the energy consumption of each sensor node and improve the efficiency of resource utilization,a DETS is adopted to regulate the frequency of data transmission.For the addressed MSNSSs,our purpose is to construct the local outlier-resistant filter under the effects of the measurement outliers and the DETS;the local upper bound(UB)on the filtering error covariance (FEC) is derived by solving the difference equations and minimized by designing proper filter gains.Furthermore,according to the local filters and their UBs,a DFF algorithm is presented in terms of the inverse covariance intersection fusion rule.As such,the proposed DFF algorithm has the advantages of reducing the frequency of data transmission and the impact of measurement outliers,thereby improving the estimation performance.Moreover,the uniform boundedness of the filtering error is discussed and a corresponding sufficient condition is presented.Finally,the validity of the developed algorithm is checked using a simulation example.
Key words: Distributed fusion filtering;Multi-sensor nonlinear singular systems;Dynamic event-triggered scheme;Outlier-resistant filter;Uniform boundedness
1 Introduction
Sensor networks (SNs) are composed of many sensor nodes,where each sensor node can detect and track the target node to obtain plenty of measurement data and then share the data with other nodes through network channels(Sun Y et al.,2022;Zhan et al.,2023).Apart from SNs,there are many dynamical systems in use that employ physical devices to achieve data exchange and communication over networks,such as multi-agent systems and Internet of Things (Ju et al.,2022;Yao et al.,2022;Chen et al.,2023;Ning et al.,2023).Among them,it is of great significance to efficiently deal with data collected from SNs and obtain state information when a large quantity of data are translated on the Internet with limited bandwidth.As such,the estimation/filtering issue with regard to SNs has received much attention,and many results have been reported for normal systems over SNs (Li Q et al.,2020;Sun Y et al.,2022;Wen et al.,2022;Hu et al.,2023d).However,studies of handling singular system (SS) estimation issues are still limited,and deserve further investigation.
Over the past few decades,the issue of state estimation/filtering for SSs has received great interest accompanying the rapid developments in robotic,aerospace,economics,and communication technologies (Dai,1989).Specifically,note that such dynamical systems have a more general form than normal systems,and that the state estimation problem becomes more difficult and complicated to address.Although the Kalman filter method is a classic filtering method,it cannot be directly used for SSs(Nikoukhah et al.,1992;Li XG et al.,2022).Accordingly,much effort has already been made to tackle this issue,and some approaches have been proposed(Wang X and Sun,2017;Cai and Chang,2023;Hu et al.,2023a).Among them,there are two commonly used methods for handling this problem.One way is the reduced-order approach,in which the reducedorder Kalman filter has been designed in Wang X and Sun (2017) for linear SSs in terms of the singular value decomposition strategy.The other method is the full-order approach,which can write the SS as an equivalent normal system under certain restrictions (Sun SL and Ma,2007;Hajmohammadi and Mobayen,2019).Compared with the reducedorder approach,the full-order approach can be used in SSs with lower dimensions.In addition,to obtain much more valuable information,the problems of distributed fusion filtering (DFF) and weighted measurement fusion filtering have been investigated in Sun JB et al.(2012) and Dou and Ran (2019) for linear multi-sensor SSs,respectively,where the fusion filters were derived by using the reduced-order approach.
According to the literature,an initial assumption on the estimation/filtering issue is that the measurement information from the sensor node is completely accurate.In many actual applications,however,such an assumption cannot be commonly ensured because the underlying system is always affected by sensor fault,missing measurements,measurement outliers,and other phenomena.If not handled properly,these issues can seriously influence the reliability of the system,and then a great number of corresponding results have been proposed(Ma LF et al.,2021;Jin and Sun,2022;Wang YZ et al.,2022).Compared with other phenomena,when networked systems are influenced by cyberattacks and sensor failures,the measurement information may generate abnormal values,which is usually called the measurement outlier phenomenon.Accordingly,the analysis and synthesis issues with respect to networked systems subject to measurement outliers have stirred more attention(Xie et al.,2022;Zhao et al.,2022;Zou et al.,2022;Ge et al.,2023a).Obviously,traditional filtering algorithms are not appropriate for systems subject to measurement outliers.In this regard,it is of great significance to design an outlier-resistant estimation scheme,in which the constructed estimator is insensitive to measurement outliers.Therefore,much effort has been made to tackle this challenging task(Alessandri and Zaccarian,2018;Jiang et al.,2021;Shen et al.,2021).For example,the filtering problem has been addressed by Shen et al.(2021) for multi-sensor multi-rate linear systems suffering from measurement outliers,where the outlier-resistant estimator has been given by using an innovative saturation strategy to reduce the effect of measurement outliers.Another outlier-resistant estimator was designed in Jiang et al.(2021) for nonlinear systems with measurement outliers,which involves an innovative self-adaptive saturation approach.However,to our knowledge,the DFF problem has seldom been addressed for multi-sensor nonlinear SSs in the presence of measurement outliers,which motivates our current study.
In another research field,the developments in communication technology and the increase in network information have caused a great deal of data to be transmitted in network channels,which can cause packet collisions and data losses due to network bandwidth (Jin and Sun,2022).An effective approach in handling this situation is to adopt a communication scheduling strategy in network channels to regulate data flow and save network resources (Wang XL et al.,2022;Ge et al.,2023b;Zhang et al.,2023).Some classical communication scheduling strategies include,but are not limited to,the Round-Robin protocol,random access protocol,try-once-discard protocol,static event-triggered scheme(SETS),and dynamic eventtriggered scheme (DETS) (Tan et al.,2017;Zou et al.,2021;Ge et al.,2022;Li JX et al.,2022;Meng et al.,2022;Hu et al.,2023c).Compared with SETS,DETS can further reduce the frequency of transmission signal,which can be considered as a valid method to decrease energy consumption and network costs,since a dynamic variable has been involved(Girard,2015).As such,a great deal of effort has been expended to investigate the DETS estimation issues(Li Q et al.,2020;Ma L et al.,2020;Jiang et al.,2022).For example,a DETS-based estimation algorithm was developed in Ma L et al.(2020) for linear singularly perturbed systems subject to distributed time delays.In addition,for multi-sensor nonlinear normal systems with the DETS,the distributed filtering and DFF issues have been tackled(Li Q et al.,2020;Hu et al.,2023b).Nevertheless,the DFF problem has not been completely handled for multi-sensor nonlinear SSs under the DETS,which further motivates our investigation.
This paper aims at developing an outlierresistant DFF algorithm for a class of time-varying multi-sensor nonlinear SSs subject to measurement outliers under the DETS.To be specific,the concerned issue is studied according to recent works(Jiang et al.,2021;Hu et al.,2023b).Nevertheless,in comparison to the results in Hu et al.(2023b),where the addressed system under the DETS was a standard nonlinear stochastic system,in our work,the DETS is considered for nonlinear SSs and the design of a local filter in Hu et al.(2023b) can be regarded as a special design of this paper when its saturation condition is ignored.Unlike the work of Jiang et al.(2021),the multi-sensor nonlinear SSs and DETS are taken into account.In addition,the local filter with the innovation saturation condition in this paper is constructed under the DETS.Hence,the presented DFF algorithm enriches existing results and could save network resources.In view of the foregoing analysis,the aims of this paper are as follows: (1) determine how to design a unified approach for nonlinear SSs with measurement outliers and DETS;(2) determine how to implement a proper DFF algorithm that can mitigate the effects of measurement outliers and the DETS concerning filtering performance;(3) determine how to provide a suitable condition to guarantee the uniform mean-square boundedness of the filtering error through theoretical analysis.To address these aims,our main contributions are as follows: (1) a uniform model framework is established for nonlinear SSs in the presence of measurement outliers and the DETS using the full-order approach;(2)a DFF algorithm is developed in terms of the inverse covariance intersection(ICI)fusion method;(3)the upper bound(UB)on the local filtering error covariance (FEC) is obtained,which can be minimized by selecting proper local filter gains;(4) a sufficient condition ensuring the uniform boundedness of filtering error in a meansquare sense is presented.
Notations: Rnis used to depict thendimensional Euclidean space.N stands for the integer set.tr(A)means the trace of matrixA.IandIkdenote the unit matrix with an appropriate dimension and thek-dimensional unit matrix,respectively.‖y‖denotes the Euclidean norm of vectory.BTandB-1represent the transpose and inverse of matrixB.E{y}refers to the expectation of the random variabley.min{a,b}and max{a,b}stand for the minimum and maximum values between two variablesaandb,respectively.
2 Problem formulation
We consider the following class of multi-sensor discrete time-varying nonlinear SSs:
wheref ∈N stands for the sampling time,xf ∈Rnrepresents the state vector to be estimated,yi,f ∈Rmstands for the measurement information with respect to theithsensor node,ϖf ∈Rvandμi,f ∈Rmare process noise and measurement noise,which are Gaussian white noises with zero means and covariancesQfandRi,f>0,respectively,and,,andCi,frepresent the given matrices with proper dimensions.
The nonlinear functionh′(xf)∈Rnis a timevarying vector withh′(0)=0 and satisfies the following condition:
forxf,zf ∈Rn,whereα>0 is a known scalar.
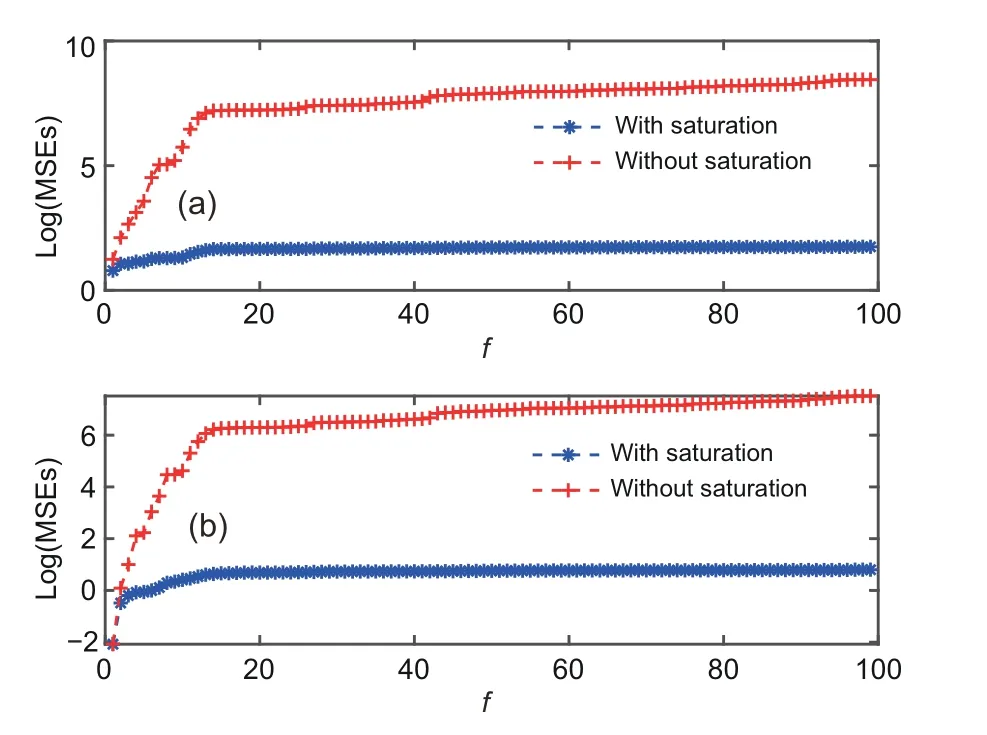
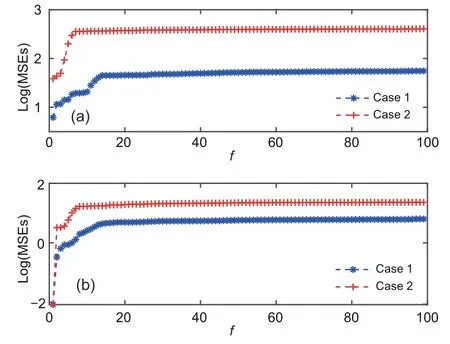
Assumption 1Kis a singular square matrix,i.e.,rank(K)=n1 Assumption 2System (1) is regular,i.e.,det(τK-)≠0,whereτis an arbitrary complex number. Assumption 3System (1) is causal,i.e.,deg(det(τK-))=rank(K),whereτis an arbitrary complex number. Assumption 4MatricesKandCi,fsatisfy rank Assumption 5The initial valuex0is independent of the random variablesϖfandμi,f,and it has meanand covarianceP0.Furthermore,the noncentral second-order moment of the initial valuex0is.Moreover,for anyf>0,the system statexfsatisfies the following condition: wherew1is a known constant. Remark 1In Assumption 5,the assumption of independence among random variables is made and then can allow for simplifications in the mathematical modeling and computation of the estimation process.In addition,for the standard state space system,the evolution process of the state system is easy to obtain.That is,the specific result ofcan be derived by using the state equation with a recursive structure.However,according to Eq.(1),we cannot straightway obtain the evolution process of the state.An elegant approach is presented to assume a UB of,which allows for the derivation of subsequent mathematical formulas.Without loss of generality,the variations of states of most systems are within certain ranges in some situations,which can be the case by considering the physical constraints,engineering requirements,and so on. To alleviate the network congestion and allocate the network resource reasonably,the DETS is introduced into communication networks,which can determine whether the measurement information with regard to each sensor is transmitted to the remote estimator or not.Specifically,the triggering instant sequence is denoted by 0≤<···<<···,wheresatisfies the following rule: withϱi>0 andβi>0 being scalars.εi,f=is the latest transmitted measurement,andφi,frepresents an internal dynamic variable that meets the following condition: whereξi>0 is a given constant and≥0 is the known initial value. Remark 2Whenβi →+∞,condition (5) can be turned into the traditional SETS as in Tan et al.(2017).Therefore,we can see that the SETS is a special case of the DETS.Based on the above description of the DETS,some features of the DETS are listed as follows: (1) the DETS allows for more flexibility in terms of changes of the dynamic variableφi,f,thereby reducing the transmission overhead;(2)in resource-constrained environments,the DETS can be regarded as a valid scheme to optimize resource utilization and save energy consumption;(3)the DETS can be effectively applied in distributed systems because each sensor node has a different triggering condition based on its own measurement and error. In multi-sensor networked SSs,the desired filter cannot be designed directly in the light of SSs (1)and(2).To tackle this problem,the full-order transformation approach that can transform the SSs into nonsingular systems is used based on the results of Sun SL and Ma (2007) and Hajmohammadi and Mobayen (2019).Specifically,in accordance with Assumption 4,there exists a full row-rank matrixsuch that Remark 3With the method in Hajmohammadi and Mobayen (2019),matricesUandVi,fcan be calculated by means of the singular value decomposition approach;that is,the solution of Eq.(7)can be deduced as follows: whereΣis an arbitrary matrix,which can be derived to guarantee thatUis of full rank.In addition,the symbol“†”represents the pseudo-inverse of a matrix. Combining Eqs.(2) and (7),SS (1) can be rewritten as As pointed out in the introduction,the phenomenon of the measurement outlier is inevitable in engineering applications,which may result in a significant degradation of filter performance if it is not dealt with reasonably.To mitigate the potential negative impact on measurement outliers in multisensor networked SSs,an innovation saturation approach with a self-adaptive threshold is exploited to design the local filter.Accordingly,theithfilter is established as follows: is a scalar with the initial value,andγi ∈(0,1),Zi=>0,and>0 are appropriate parameters. The main objective of this paper is to construct the local filter as in Eqs.(10) and (11).In addition,under the DETS,the UB of the local FEC is obtained and then minimized by designing the proper filter gain in each processor.In view of the local filters and UBs of the FEC from all processors,we look for the distributed fusion filter (FF)and FECbased on the ICI fusion method described in Noack et al.(2017).Moreover,the boundedness regarding the filtering error is investigated and analyzed by proposing a sufficient criterion.To clarify the research issue,the diagram of the system framework is shown in Fig.1. Fig.1 Diagram of the system framework In this section,we develop an outlier-resistant DFF algorithm for nonlinear SSs with measurement outliers and DETS by using the ICI fusion criterion. To proceed,the following lemmas are introduced: Lemma 1For anyb1,b2∈Rn,one has whereϕ>0 is a scalar. Lemma 2(Jiang et al.,2021) For anyc1,c2∈R,there exists a real numberλ ∈[0,1] satisfying whereSπ(·) denotes the saturation function described in Eq.(12). Lemma 3(Li Q et al.,2020) For alli ∈{1,2,···,κ},suppose thatξiβi ≥1 is true and letai,f>0 andbi,f>0 be given scalars.The variables Based on Lemmas 1–3 and some definitions,the recursion expressions of estimation error covariances are provided as follows: Theorem 1For sensori(i=1,2,...,κ),the local PECΓi,f+1|fand FECΓi,f+1|f+1with the initial valueΓi,0|0=P0have the following forms: where ProofFor brevity,the proof of Theorem 1 is omitted here. Theorem 2For each sensor subsystem,let scalarsϕq1>0 (q1=0,1,...,13) be given.If the following two difference equations then it can be derived that Furthermore,if the local filter gain is expressed as then it can be verified that the UB of the FEC is minimized at each moment. ProofTheorem 2 is proved by using the mathematical induction approach.Specifically,based on the initial condition,we have>0.In what follows,suppose that the conditionholds;then we will proveΓi,f+1|f+1≤First,according to Lemma 1,the cross terms of Eq.(16) are addressed.As such,we have withϕ1–ϕ5being positive scalars.In terms of inequality (3),the uncertain term of inequality (22)can be tackled as whereα>0 is a scalar.In view of inequality(4)and Lemma 1,the other uncertain term of inequality(22)is addressed as whereϕ0>0 is a scalar.It follows from inequalities(23) and (24) that Next,we will check thatΓi,f+1|f+1≤Using Lemma 1,the cross terms of Eq.(17) can be tackled,and then we can obtain whereϕq2(q2=6,7,...,10) are positive scalars.From Eq.(5) and Lemma 3,the uncertain term of inequality(26)can be handled as Noticing the other uncertain term of inequality(26),it follows from Eqs.(13)and (14)that It follows from Lemma 1 that whereϕ11,ϕ12,andϕ13are positive scalars.By substituting inequality (29) into inequality (28),we have According to inequalities (27) and (30),we have Based on the induction method,Eqs.(16) and (17),and inequalities(25)and(31),it can be inferred that To proceed,the minimized UB on the FEC will be derived.Specifically,let,and then the local filter gain is derived and depicted in Eq.(21).Consequently,the proof is complete. In what follows,we aim to construct FF and FEC for the considered nonlinear SSs.Note that the local expressions of the cross-covariance on the estimation error cannot be deduced easily;the ICI fusion method described in Noack et al.(2017) is adopted,which uses only the UBs of the estimation error covariance from each processor. In accordance with the local filteri,f|fand its UB(i=1,2,...,κ),the recursive forms concerning the ICI-based FFand its covarianceare shown as follows: In addition,the DFF algorithm can be transformed into the following optimization problem: By using the optimization toolbox from MATLABⓇ,we can derive the solution of problem (35). In the sequel,we will test the developed fusion algorithm in view of the ICI fusion rule,and the following theorem is presented: Theorem 3For the multi-sensor SSs (1) and(2)with local known UBs on the FEC,the ICI-based fusion method in Eqs.(32)–(34) holds and satisfies the following condition: ProofFor each sensor node,we have the results that(i=1,2,...,κ).The proof is easily checked,and the details are omitted for brevity. To facilitate implementation,the procedure of the DETS-based DFF (DETSBDFF) algorithm is given in Algorithm 1. In this section,we discuss the performance with respect to the designed DFF algorithm.A sufficient condition that can guarantee the uniform boundedness of the filtering error in the mean-square sense is presented.To handle this case,the following assumption is needed: Assumption 6For any sensori(i=1,2,...,κ)and timef,there exist positive numberssuch that the following conditions hold: Furthermore,some notations are given as To proceed,the other scalarsϕq1(q1=0,1,···,13) are considered as fixed values for any time.Based on Assumption 6,a sufficient condition is presented in the following theorem,which can ensure that the filtering error is uniformly bounded in the mean-square sense: Theorem 4Consider the time-varying multisensor SSs depicted in Eqs.(1) and (2).Under Assumption 6 and notations (37),if the inequality conditionχ′≤holds with the initial conditionholds for anyf. ProofThis theorem can be readily checked by using the mathematical induction approach,and its proof is omitted for the sake of conciseness. Remark 4It is easy to deduce thatIt follows from the Schur complement lemma that we can obtainThen,the uniform boundedness regarding the filtering error in the mean-square sense is verified. In this section,a simulation example is presented to show the usefulness of the proposed DFF algorithm. We consider a time-varying nonlinear SS with three sensors,and its parameters are given as The nonlinear function ish′(xf)=[0 0.172sin(x2,f)]T,where the system state isxf=[x1,f x2,f]T,and the constant is chosen asα=0.172 according to inequality(3). In the simulation,we select the initial values=2I2.The system noises are zero means and their variances are taken asQf=0.1,R1,f=0.151,R2,f=0.21,andR3,f=0.122.The other parameters are chosen asw1=2,ai,f=bi,f=0.1(i=1,2,3),andϕq1=0.1 (q1=0,1,...,13).Considering the DETS and adaptive saturation constraint condition,the relevant parameters are taken asφi,0=1,ϱ1=0.46,ϱ2=0.51,ϱ3=0.41,βi=15,ξi=0.1,γi=0.45,=0.5,=5,Λi,f=1,andZi=0.1 (i=1,2,3).Furthermore,the outlier depicted by the zero-mean noise with variance 10 is taken into account in the simulation,and we assume that the time period of the appeared outliers isT=5. According to the above parameters,the simulation results are shown in Figs.2–8.Fig.2 shows the curves of the actual state and its fusion filtering.Fig.3 displays the logarithm of mean square errors(MSEs)with respect to the FF and three local filters.Fig.4 plots the curves of the logarithm of UB traces on the fusion FEC and local FEC.It can be seen that the performance of the FF is better than those of the other local filters.Accordingly,it is easy to see that the curves of log(MSEs) always stay below their UBs. Fig.2 Actual state and fusion filtering: (a) the first state component;(b) the second state component Fig.3 Log(MSEs) of the fusion filter and three local filters: (a) the first state component;(b) the second state component Fig.4 Logarithm of UB traces of the fusion filter and three local filters: (a) the first state component;(b)the second state component To further verify the validity of the proposed approach,the curves of log(MSEs)of the FF with or without the adaptive saturation condition are shown in Fig.5.Fig.6 displays the curves of log(MSEs)of the FF when the variances of the outlier are chosen as 10 and 20;i.e.,in case 1,the variance of the outlier is 10 and in case 2,the variance of the outlier is 20.Furthermore,to demonstrate the impact of the measurement outlier on the UB of the FEC,Fig.7 shows the curves of the logarithm of UB traces on the fusion FEC in the above two cases.It can be seen that the UBs become slightly larger with the increase of the outlier variance,and hence the presented approach can further mitigate the influence of outliers on estimation performance.According to comparison results from Figs.5–7,we see that the presented approach with the outlierresistant method performs better than the approach without the outlier-resistant method.In addition,to compare the effect of the DETS with that of the SETS,Fig.8 shows the triggering instants of each node under the DETS and SETS.As expected,it is easy to see that the DETS can further reduce the communication burden.In view of the above results,the provided DFF algorithm is effective. Fig.5 Log(MSEs) of the fusion filter with or without adaptive saturation condition: (a) the first state component;(b) the second state component Fig.6 Log(MSEs) of the fusion filter in two cases:(a) the first state component;(b) the second state component Fig.7 Logarithm of UB traces of the fusion filter in two cases: (a) the first state component;(b) the second state component Fig.8 Event-triggered time of each node under the DETS (a) and SETS (b) In this paper,the outlier-resistant DFF issue has been tackled for a class of multi-sensor nonlinear SSs with measurement outliers and a DETS.In view of the stochastic analysis method,a local UB with respect to the FEC has been deduced,and the filter gain has been computed by minimizing the trace of the obtained UB.On the basis of the local filters and their UBs,the outlier-resistant fusion filtering approach has been implemented using the ICI fusion method.In addition,a sufficient condition that can ensure the boundedness of the filtering error has been presented.Furthermore,the potential research work includes the extension of the main results to handle other communication scheduling strategies,such as the try-once-discard strategy and encoding–decoding strategy(Shen et al.,2021;Zou et al.,2021;Jiang et al.,2022). Contributors Jun HU designed the research.Zhibin HU drafted the paper and performed the simulation example.Cai CHEN,Hongjian LIU,and Xiaojian YI helped organize the paper.Jun HU revised and finalized the paper. Compliance with ethics guidelines All the authors declare that they have no conflict of interest.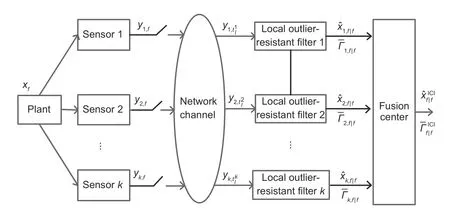
3 Main results
3.1 Derivation of the local FEC
3.2 Fusion filtering method

4 Boundedness analysis
5 An illustrative example





6 Conclusions
 Frontiers of Information Technology & Electronic Engineering2024年2期
Frontiers of Information Technology & Electronic Engineering2024年2期
- Frontiers of Information Technology & Electronic Engineering的其它文章
- Towards resilient average consensus in multi-agent systems:a detection and compensation approach∗&#
- Modified dynamic event-triggered scaled formation control for multi-agent systems via a sparrow search algorithm based co-design algorithm∗
- Event-triggered distributed optimization for model-free multi-agent systems∗#
- Event-triggered finite-time command-filtered tracking control for nonlinear time-delay cyber physical systems against cyber attacks∗
- Recursive filtering of multi-rate cyber-physical systems with unknown inputs under adaptive event-triggered mechanisms∗#
- Estimation of Hammerstein nonlinear systems with noises using filtering and recursive approaches for industrial control*
