Estimation of Hammerstein nonlinear systems with noises using filtering and recursive approaches for industrial control＊

Mingguang ZHANG ,Feng LI†‡ ,Yang YU ,Qingfeng CAO

1School of Electrical &Information Engineering, Jiangsu University of Technology, Changzhou 213001, China

2College of Electrical, Energy and Power Engineering, Yangzhou University, Yangzhou 225127, China

Abstract: This paper discusses a strategy for estimating Hammerstein nonlinear systems in the presence of measurement noises for industrial control by applying filtering and recursive approaches.The proposed Hammerstein nonlinear systems are made up of a neural fuzzy network (NFN) and a linear state–space model.The estimation of parameters for Hammerstein systems can be achieved by employing hybrid signals,which consist of step signals and random signals.First,based on the characteristic that step signals do not excite static nonlinear systems,that is,the intermediate variable of the Hammerstein system is a step signal with different amplitudes from the input,the unknown intermediate variables can be replaced by inputs,solving the problem of unmeasurable intermediate variable information.In the presence of step signals,the parameters of the state–space model are estimated using the recursive extended least squares (RELS) algorithm.Moreover,to effectively deal with the interference of measurement noises,a data filtering technique is introduced,and the filtering-based RELS is formulated for estimating the NFN by employing random signals.Finally,according to the structure of the Hammerstein system,the control system is designed by eliminating the nonlinear block so that the generated system is approximately equivalent to a linear system,and it can then be easily controlled by applying a linear controller.The effectiveness and feasibility of the developed identification and control strategy are demonstrated using two industrial simulation cases.

Key words: Hammerstein nonlinear systems;Neural fuzzy network;Data filtering;Hybrid signals;Industrial control

1 Introduction

Recently,the accelerated advancements in the domains of computing,communication,and control have brought about substantial transformations in human society.In the context of Industry 4.0 and intelligent manufacturing,industrial cyber-physical systems(ICPSs) are thriving due to their unique advantages.ICPSs concentrate on the seamless integration and synchronization of computing resources with physical resources,primarily applied in various intelligent systems such as robotics (Huang J et al.,2022),smart grid (Wen et al.,2021;Ning et al.,2023),and smart transportation (Ge et al.,2022,2023;Xie et al.,2023;Zhang XM et al.,2023).If effective optimization control strategies cannot be formulated,the control strategy will inevitably affect the smooth operation of ICPS and even reduce the safety of the systems(Zhang H et al.,2018).Within the realm of control systems,almost all systems have certain nonlinear characteristics (Wang YJ and Yang,2021).Amid the relentless advancement of contemporary technology,the nonlinearity and complexity of control objects continue to increase,and many advanced control methods require mathematical models of nonlinear systems (Xu et al.,2015;Xu,2016;Zhang HY et al.,2021).

Hammerstein systems are typical block-oriented models,the basic structure of which is a static nonlinear block connected to a dynamic linear block (Hou et al.,2023;Janjanam et al.,2023;Zhao et al.,2023).It has a simple structure and can describe various typical nonlinear processes,such as the heating process(Hammar et al.,2019),the pH process (Li et al.,2023b),and the process of a continuous stirred tank reactor(Li et al.,2023a).Lately,some substantial estimation approaches have been proposed for the Hammerstein systems.These approaches can be broadly bifurcated into two classes—those that directly calculate each indeterminate parameter within the Hammerstein systems (Filipovic,2019;Ma JX et al.,2020;Wang DQ et al.,2020) and those that independently estimate each block parameter of Hammerstein systems by reconstructing the internal unmeasured variable (Chen and Chen,2011;Kothari et al.,2020;Li et al.,2023c).

Noise generally exists in practical applications,and the noise in actual industrial processes is rarely white noise that conforms to a normal distribution.Consequently,exploring estimates of Hammerstein systems under the influence of noise interference becomes paramount.Data filtering is usually used to get rid of the outliers and weaken the influence of noise in linear and nonlinear systems,and has been applied to identify model parameters (Wang DQ et al.,2013;Ding et al.,2015;Ma JX et al.,2016;Ji et al.,2021;Shi et al.,2023).The principle of data filtering is to filter the input–output data of a system using a linear filter;it should be emphasized that this technique can change only the influence of output noises on the system but cannot change the structure of the system itself.To solve the multiple-input single-output Hammerstein identification problem in the presence of autoregressive noises,Ji et al.(2021) introduced the multiple-stage Levenberg–Marquardt method based on the data filtering technique and the hierarchical identification principle,which can decrease the influence of noise on parameter estimation.The investigation of Wang DQ et al.(2013) focused on a fresh parameter estimation method for Hammerstein systems with output noises,using a recursive least squares (RLS)algorithm with a key-term separation principle and data filtering technique.To enhance the convergence rate and the precision of parameter identification,a forgetting factor stochastic gradient method based on filtering technology was proposed by Ma JX et al.(2016).We would like to point out that the approach capability of the static nonlinear block by way of polynomial modeling or a piecewise function is limited for nonlinear discontinuous functions in Wang DQ et al.(2013),Ma JX et al.(2016),and Ji et al.(2021).To alleviate the issues mentioned above,neural networks(Michalkiewicz,2012;Cui et al.,2014) and fuzzy logic systems (Khalifa et al.,2021) have been extensively used in modeling nonlinear dynamic systems due to their adeptness at capturing nonlinearity with remarkable accuracy.Cui et al.(2014) used a function link artificial neural network to model a static nonlinear function,and independently determined parameters of linear and nonlinear blocks by employing the least squares method and the Levenberg–Marquardt algorithm,respectively.Khalifa et al.(2021)introduced the autoregressive moving average and fuzzy systems,and then an identification method based on the Lyapunov function was applied for Hammerstein systems.While neural network models exhibit robust self-learning capacities,they fall short of emulating the reasoning abilities intrinsic to the human brain.Unlike neural network models,fuzzy systems lack self-learning capabilities and there are certain limitations to their practical implementation.As a result,a significant technique is to apply a neural fuzzy network (NFN) model that combines the fuzzy reasoning ability of a fuzzy system and the self-learning of neural network models as the static nonlinear block in Hammerstein systems.It is essential to recognize that the identification process for the NFN-based Hammerstein systems diverges significantly from that of a standalone NFN model.The primary distinction stems from the structural constraints dictated by the Hammerstein systems.Clearly,the identification challenge that arises demands the concurrent consideration of nonlinear mapping and linear dynamics.Conversely,research on individual NFNs primarily centers on the identification of a singular,global nonlinear mapping.

Motivated by the aforementioned methods,a methodology for estimating neural fuzzy Hammerstein nonlinear systems using data filtering technology and a recursive approach is developed in this study.Practical application processes are often disturbed by random measurement noises,and thus it is extremely significant to consider the NFN-based Hammerstein systems with measurement noises.The parameter estimate scheme presented can be delineated in the subsequent two steps.In the first step,a nonlinear block and a linear block are separated by using the characteristic that step signals are unable to activate nonlinear blocks,which avoids decomposing parameter product terms in a synchronous estimate and improves the estimation accuracy.Using input and output data derived from step signals,the parameters of the dynamic linear block are determined through the recursive extended least squares (RELS) approach.In the second step,based on input–output random signals,the cluster method is used to calculate the center and width of the NFN model.Concurrently,the weight of the NFN model is updated by employing the data-filteringbased RELS technique.

The notable innovations of this study are evident in the following aspects:

1.A novel NFN-based Hammerstein system is proposed by combining the advantages of the structure of Hammerstein systems and NFNs,and the modeling accuracy is improved compared with that of a single NFN or neural network (Cui et al.,2014).

2.Unlike synchronous estimation schemes (Hammar et al.,2019;Li et al.,2023b;Zhao et al.,2023),which contain the parameters’ product terms of the linear and nonlinear blocks,the strategy presented here decouples the parameter estimation of the nonlinear block from that of the linear block using designed hybrid signals,resulting in an enhancement of the estimation accuracy of the systems.

3.Data filtering is introduced to derive a filteringbased RELS algorithm for the Hammerstein nonlinear systems with noises,which can reduce the impact of moving average noise and improve the precision of parameter estimation.

2 System model and problem formulation

The Hammerstein systems with measurement noises (Ding et al.,2015;Li et al.,2023b),shown in Fig.1,are nonlinear systems defined by a sequential configuration of a static nonlinear block preceding a dynamic linear block.

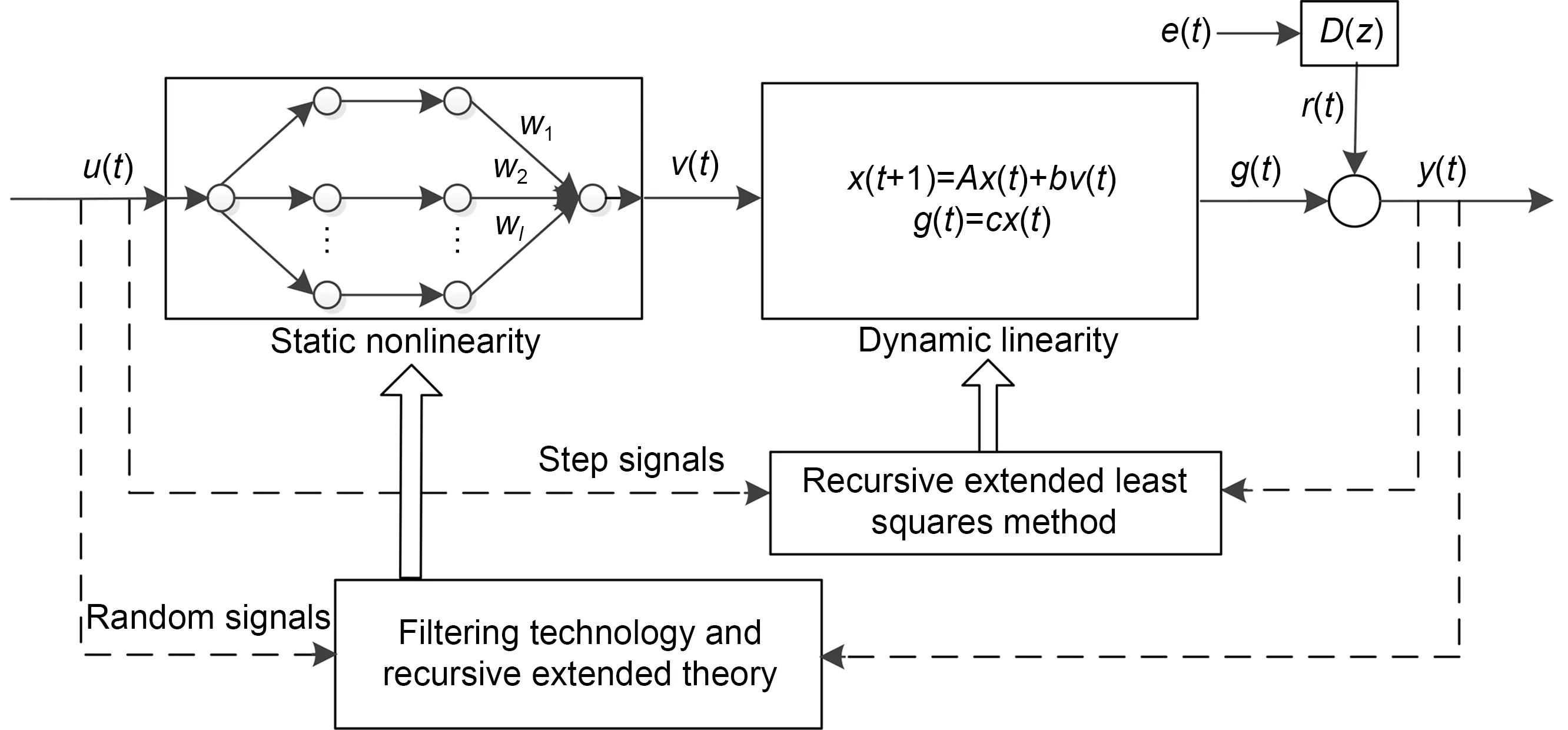
Fig.1 Hammerstein nonlinear systems

The input–output relationships can be described as follows:

where the system input and output are described asu(t) andy(t),respectively,v(t) is the output of the static nonlinear block,g(t) is the output of the linear block,r(t) indicates colored noises,ande(t) represents Gaussian noises.D(z)=1+d1z-1+d2z-2+…+dnz-nis a linear combination of backward operatorsz-1.The state space model is represented by Eqs.(2)and (3).x(t)=[x1(t),x2(t),…,xn(t)]Tis the state vector.A,b,andcare the system parameter matrix or vectors.b=[b1,b2,…,bn]T∈Rn×1,c=[1,0,…,0] ∈R1×n,and

In this paper,the nonlinear block is approximated using the NFN (Li et al.,2023b),as illustrated in Fig.1.Based on Fig.1,the NFN can be described as follows:

Definingɛas a constant threshold,the objective of the proposed parameter identification technique is to ascertain the indeterminate parameters of both static nonlinear and dynamical linear blocks.These parameters must meet the subsequent criteria:

3 Parameter estimate of Hammerstein systems

We delineate the identification procedure for NFN-based Hammerstein systems in this section.The existing research indicates that hybrid signals,comprising step and random signals,can achieve twostage identification of the Hammerstein systems integrated with the state–space model and the NFN model.Initially,the step response aids in the parameter estimate of the state–space model.Subsequently,the random input response is employed to compute the NFN parameters.

Kothari et al.(2020) elucidated that,with a step signal input to the Hammerstein systems,the nonlinear block becomes operational,leading to an amplitude variation for the consistent input.To specify,when the step input traverses a static nonlinear system,the resultant output is step signals,albeit with varying amplitudes,as illustrated in Fig.2.Consequently,the intermediate variable isv(t)=βu(t).Hence,with the introduction of a step input,each block in the Hammerstein systems can be discerned autonomously.

Fig.2 Relationship between u and v under step signals

3.1 Estimate of the dynamic linear block

When a step signalu1(t) is used to identify parameters of the linear block,based on Eq.(2),we obtain

By multiplyingz-iandz-non both sides of Eqs.(10) and (11) separately,we have

Simplifying Eq.(12),we obtain

Because of the relationship betweenuandvunder step signals,replacingv(t) withβu1(t),we have

According to Eqs.(3) and (14),we can derive

Based on Eqs.(4),(5),and (15),the outputy1(t)can be written as

Moreover,the outputy1(t) can be simplified as

However,x(t) ande(t) are unidentified variables;a viable approach entails the utilization of estimations(t) and(t) as substitutes for the unidentified variables,and thus we have

Define and minimize the mean square criterion functions:

The identification of parameterθ1is achieved using the RELS method as follows:

Thus,the parameters pertaining to the linear block are determined.

3.2 Estimate of the static nonlinear block

According to the previous analysis,the parametersandhave been identified.In this subsection,a group of random signalsu2(t) and outputy2(t) is applied to nonlinear element estimation.The centercland widthσlof NFN can be acquired by a cluster algorithm (Li et al.,2022),which is expressed by

whereNLis the number of clusters belonging toL,λ∈[0,1] is an adjustable parameter,andρ∈[1,2] denotes an overlapping parameter.

After that,the primary challenge lies in identifying the weight coefficientswl.

According to Fig.1,we can obtain a noise variable

Based on Eqs.(5) and (27),we obtain

To enhance identification precision,a linear filter 1/D(z) is employed to Hammerstein systems.It should be emphasized that the filter can change only the influence of colored noises on the system but cannot change the structure of the system itself.Based on the constant input–output relation,the structure of the systems is simplified,which can simplify calculations and improve parameter estimation accuracy(Ma L and Liu,2016).

Multiplying both sides of Eq.(28) by 1/D(z),we obtain

Define the filtered outputyf(t),filtered internal variablegf(t),and filtered inputvf(t) as

Thus,we can obtain

According to Eq.(34),we have

Note that Eq.(35) contains unknown variablesyf(t) andφf(t),and thus the identification algorithm can not be implemented.To circumvent this limitation,a viable approach entails the utilization of estimation residuals as substitutes for the unidentified variables at timet.

Define the parameter estimation of the noises model as

Thus,the estimation ofD(z) is expressed as

Furthermore,we have

So,the estimate ofr(t) is

By defining and minimizing the mean square criterion functions,the data-filteringbased RELS approach can be obtained:

To provide a clearer description of the proposed method,the detailed estimate procedure is illustrated in Fig.3.

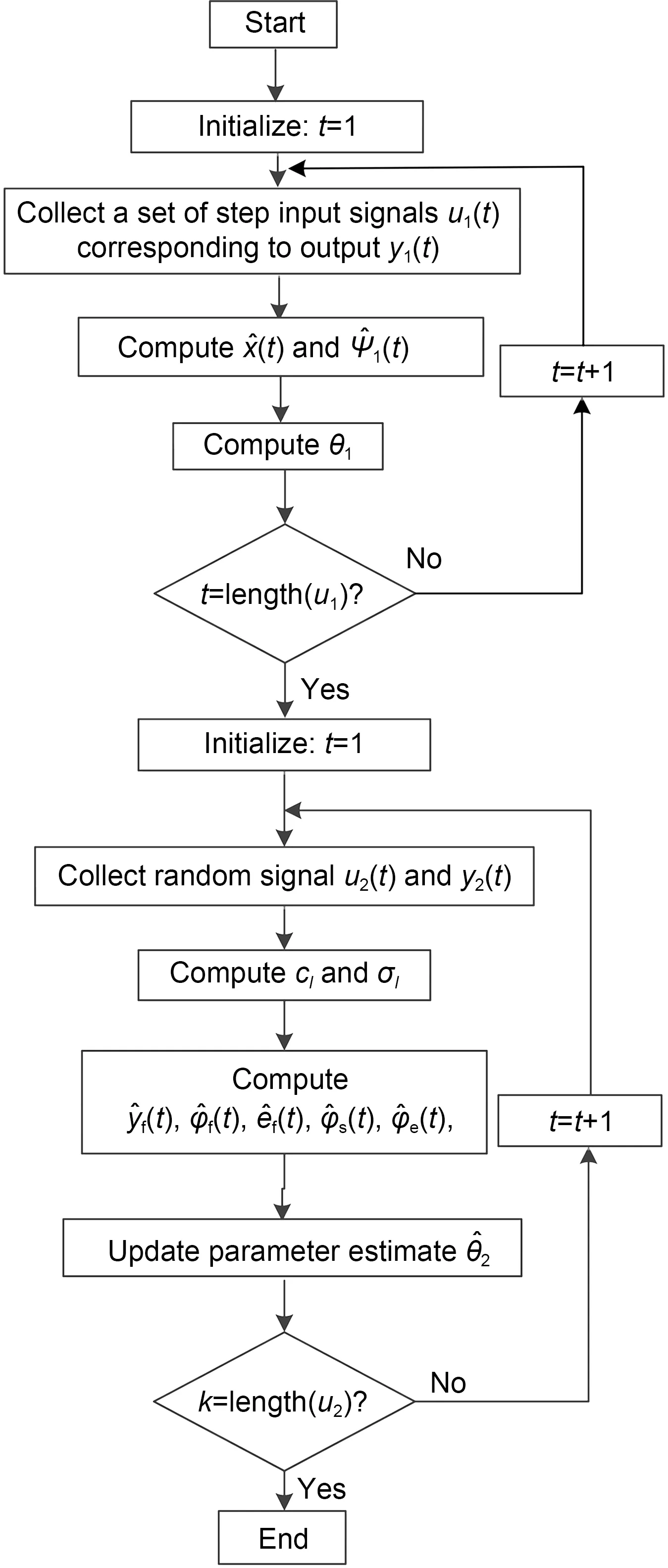
Fig.3 Flowchart of the developed parameter identification method

4 Simulation and analysis

To corroborate the efficacy and precision of the proposed parameter estimation method,two typical nonlinear processes,namely the pH nonlinear process and the continuous stirred tank reactor (CSTR),are simulated in this section.

4.1 pH neutralization process control

In the actual chemical production process,the control of pH value is often involved,and its control effect will seriously affect the purity of the substance.To corroborate the efficacy of the proposed strategy,we conduct a simulation using the pH neutralization process in chemical production (Smith et al.,2007).Fig.4 presents a diagram of the pH neutralization process.Alkaline solution uses caustic soda(NaOH),while acidic solution uses hydrochloric acid(HCl).The pH value of the neutralization tank is regulated by adjusting the flow rate of HCl.

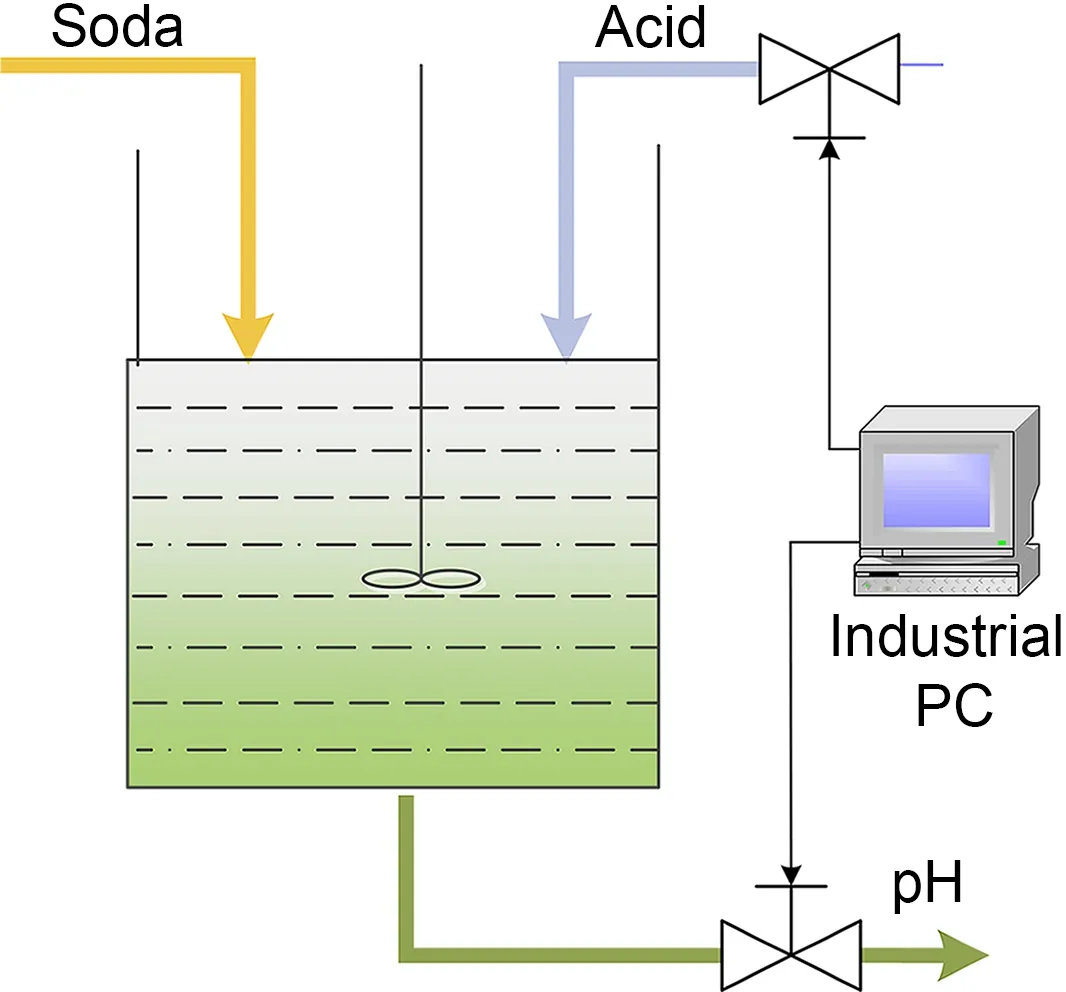
Fig.4 Process of pH neutralization

The pH model can be expressed as

Table 1 gives the nominal values of the parameters.

Table 1 Nominal values

To handle the developed identification scheme,hybrid signals,including step signals with an amplitude of 0.5 and random signals with the amplitude distribution in [-0.5,0.5],are employed to acquire the process input–output.Applying step signals to input–output,the linear dynamic block can be obtained by(t)=1.0341x2(t-2)-0.1868x1(t-2)+0.1899(t-1)+0.1899(t-2).Then,we set the parameters asρ=1.0 andλ=0.01,and obtain an identified NFN-based Hammerstein system.

The Hammerstein model serves as a structural framework for representing a nonlinear system by segregating the static nonlinear component from the dynamic linear component.Consequently,we can initially employ the identified linear parameters to estimate the intermediate variables associated with the dynamic linear portion.Subsequently,we proceed to construct the inverse model for the static nonlinear section,using both the input and the estimated intermediate variables.This approach results in an apparent linear relationship between the system’s input and output.Hence,we can effectively transform the nonlinear control problem into a linear control problem.Fig.5 illustrates the control architecture based on the identified Hammerstein system.

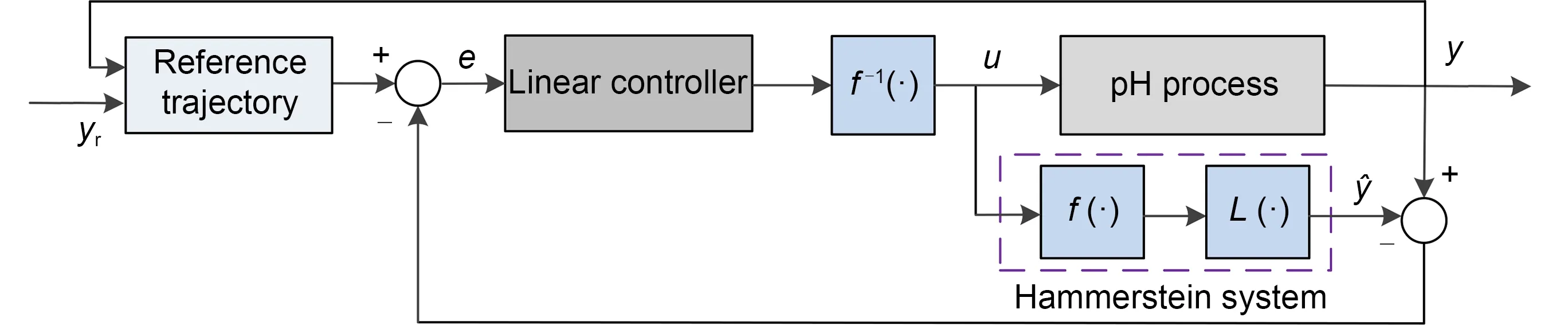
Fig.5 pH process control system

For comparison,a traditional proportionalintegral (PI) controller characterized byu(t)=u(t-1)+K[e(t) -e(t-1) +e(t)/τ],a control-based Hammerstein system using a data-filtering-based forgetting factor stochastic gradient identification algorithm(Control-H-F-FFSG) in Ma JX et al.(2016),and MPC control of the Hammerstein system (MPC-H)(Du et al.,2018) are used to control the pH process,wheree(t)=yr(t)-y(t),andyris the reference trajectory.Within this study,the controller parameters of the proposed method areK=0.6 andτ=70,and the sampling time and prediction step size of the MPC controller are set to 0.02 s and 5,respectively.The pH control results with different values using different methods are shown in Fig.6.

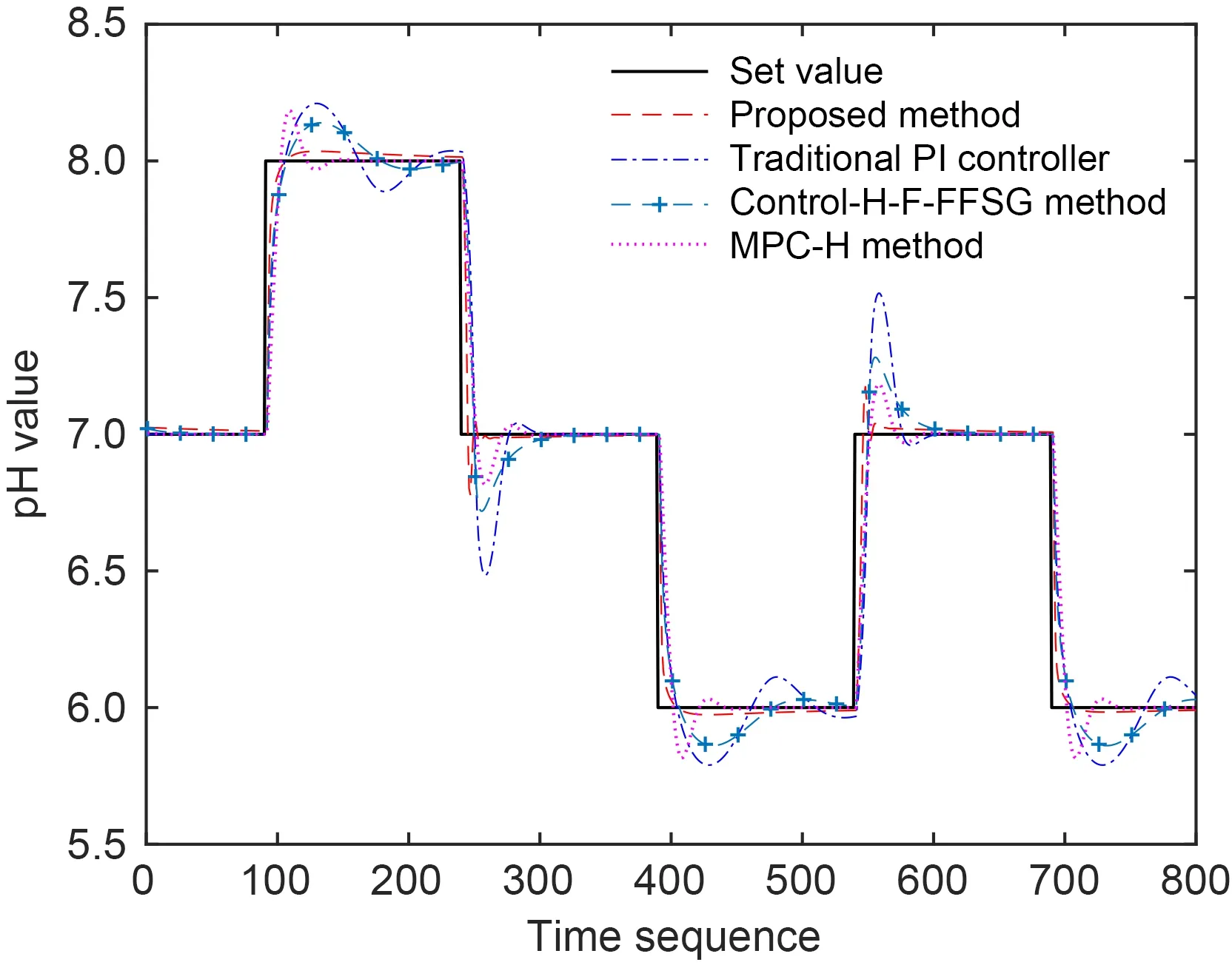
Fig.6 Set value tracking output response

As can be easily seen in Fig.6,the proposed control system using an estimated NFN-Hammerstein system manifests a superior control performance in contrast to the traditional PI controller,the MPC-H method,and the Control-H-F-FFSG method.In general,for selecting different pH values,the presented control method can track,with effect,the set values with better overshoot and a higher response speed.To be specific,when the pH value is 8,the overshoot of the proposed control method is reduced compared to the traditional PI controller,the MPC-H method,and the Control-H-F-FFSG method.Thus,the developed NFN-Hammerstein system provides a feasible scheme for the design of the control system.

4.2 CSTR control

Due to the strong nonlinearity of the production process of the chemical CSTR systems,traditional linear control cannot meet the standards required for industrial production efficiency.Therefore,for the control of CSTR systems,it is necessary to switch ideas and adopt control methods that are more suitable for nonlinear system control,thus improving the control efficiency and economic benefits of the CSTR system’s chemical production process.In this example,we consider a CSTR process (Jia et al.,2005),and its dynamic characteristics are as follows:

Table 2 lists the kinetic parameters.

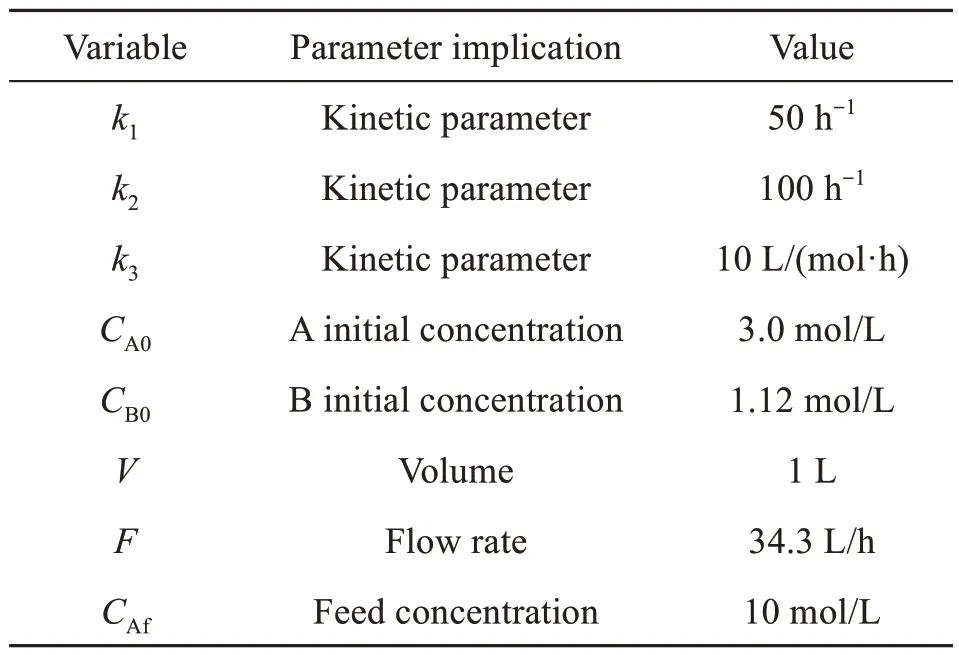
Table 2 Kinetic parameters

We use step signals and random signals,as illustrated in Fig.7,to obtain the input–output data for the CSTR,and the data are normalized.Based on the step signals,the expression of the linear block can be obtained by(t)=0.2277x2(t-2)-0.1339x1(t-2)-0.0326(t-1)+0.0018(t-2).Next,for NFN identification,we set parametersρ=1.0 andλ=0.01.Thus,the NFN parameters can be identified by using the proposed scheme.

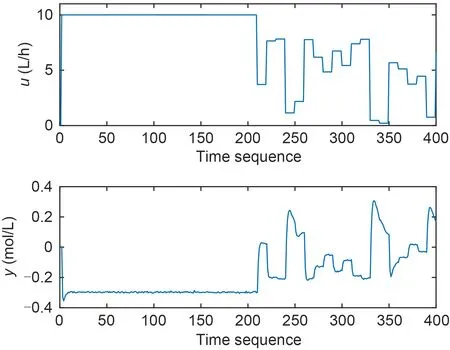
Fig.7 Input–output data of CSTR

The identified NFN-based Hammerstein system is employed for concentration control for CSTR.The design principle of the control system is similar to that of the pH neutralization process.Currently,the controller parameters withK=0.15 andτ=0.6 are chosen,and the sampling time and prediction step size of the MPC controller are 0.02 s and 5,respectively.To verify the performance of the proposed control system,the traditional PI controller,the Control-H-FFFSG method,and the MPC-H method are used for comparison,and the control results of the concentration and inlet flow rate using different methods are illustrated in Fig.8.

Fig.8 Results of setting value 0.1

According to Fig.8,when the set point is 0.1,the set value is obtained at a high speed and with a short adjustment time by applying the designed controller based on the estimated NFN-Hammerstein systems.In contrast,the traditional PI controller,MPCH method,and Control-H-F-FFSG method need more time to reach the set value.In terms of adjustment time,the proposed method has a noticeable reduction compared with the MPC-H method,Control-H-F-FFSG method,and traditional PI controller,which further proves the validity of the proposed control scheme.

5 Conclusions

In this paper,we propose an identification strategy for Hammerstein nonlinear systems for industrial application by applying data filtering and a recursive approach.The two main advantages of the presented scheme are: (1) leveraging the step signals’ trait of not stimulating the nonlinear characteristic,the parameters of both linear and nonlinear blocks are independently identified using hybrid signals;(2) a data filtering technology is used for Hammerstein system identification,therefore reducing the impact of measurement noises and improving identification accuracy.In our future work,two aspects will be addressed.On one hand,for the Hammerstein system with colored measurement noise interference,we will improve the identification accuracy by estimating the variance of the noise.On the other hand,we will expand the application scope of the proposed method to control more nonlinear systems,such as power grid systems(Yang et al.,2021;Huang G et al.,2022) and permanent magnet synchronous motors (Xiao et al.,2022).

Contributors

Mingguang ZHANG and Feng LI designed the research and drafted the paper.Mingguang ZHANG,Feng LI,Yang YU,and Qingfeng CAO revised and finalized the paper.

Compliance with ethics guidelines

Mingguang ZHANG,Feng LI,Yang YU,and Qingfeng CAO declare that they have no conflict of interest.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.