高超声速有攻角锥裙直接数值模拟

赖江，范召林，王乾，董思卫，童福林，*，袁先旭

1.中国空气动力研究与发展中心 空气动力学国家重点实验室，绵阳 621000

2.中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

3.中国空气动力研究与发展中心，绵阳 621000

高速飞行器内外流动中激波/边界层干扰（Shock Wave/Boundary Layer Interaction， SWBLI）现象广泛存在，对气动力热载荷具有巨大影响，尤其在高超声速领域，干扰区流动分离/再附会导致局部极高热流、摩阻，可能诱发热力学和结构方面的问题，严重威胁飞行安全［1-4］。因此，激波/边界层干扰的物理机制不仅是空气动力学中亟待解决的关键基础科学问题，在航空航天工程应用领域的重要性也不言而喻。

Gaitonde［3］、Gaitonde 和Adler［5］总 结 了 激波/边界层干扰研究的典型标模，包括引入外部激波的反射干扰，自身诱发激波的压缩拐角、轴对称柱裙/锥裙，以及具有三维特征的后掠拐角和单楔/双楔等构型。针对反射激波干扰和压缩拐角这类二维构型已有大量公开发表的风洞试验和数值模拟研究，对激波/边界层干扰问题的认识已取得了较大的进展。例如，Pirozzoli 和Grasso［6］获 取 了 马 赫 数Ma∞=2.25 反 射 激 波 干扰中的流动分离、湍流增强、激波振荡等现象并开展了相应机制分析，还提供了包含速度和压力分布、湍动能输运的精细流场数据库［7］。Clem⁃ens 和Narayanaswamy［8］、范孝华等［9］对激波低频振荡研究进行综述时指出，该现象可能由上游湍流边界层的脉动驱动，也可能与下游分离流固有的不稳定性有关。干扰区低频非定常性的来源取决于流动分离区的尺寸，较大分离中由下游机制占主导，而较弱分离中则是上游和下游机制同时存在。Fang 等［10］对湍流增强机制进行了综述，总结了早期包括激波非定常运动、激波/湍流直接干扰、声波和熵波的产生、自由剪切层等各种可能的原因。随着高速试验技术和数值模拟方法的发展，自由剪切层被普遍认为是SWBLI 中湍流增强的主要因素。童福林等［11］通过分析比较3 个不同展向站位分离泡的非定常运动特性、分离微团几何特征和相干结构等，定量给出了三维展向结构差异的影响规律。

随着高超声速飞行器的发展，对探明激波低频振荡原因、预测流动分离特征、发展减阻降热技术等方面的需求越发强烈和迫切，但目前对上述部分问题认识尚不充分或还存在争议。尤其是现有大多研究针对二维构型，必然会忽略三维特征，在数值模拟中还无法避免展向计算域和边界条件等导致的误差，从二维构型研究得到的结论在三维情况下的有效性和适用性也尚不明确，已不能涵盖工程实际中面临的问题和困难，因此需要面向更加接近工程实际的构型开展相关研究。

锥裙构型是SWBLI 的研究标模之一［3］，是高超声速再入飞行器和导弹等的有效简化，是本文所选取的计算构型。根据上游边界层状态，锥裙拐角附近流场可分为激波与层流边界层干扰、激波与转捩/湍流边界层干扰。针对第1 类问题，大量试验研究以25°～55°为典型几何参数，着重刻画干扰流场结构特征。Holden［12］归纳相关试验研究，重点讨论了Ma∞=10～12，雷诺数Re∞≈104～105条件下干扰区的热流和压力分布。Wright［13］、Nompelis［14］等刻画了以激 波系统 为主的干扰流场，包含前锥上游的斜激波、分离激波，裙结构上的输运激波、再附激波、弓形激波等，还给出了分离区、接触面、超声速喷流、声速线、三叉点等典型结构。Candler［15］、Tumuklu［16］等采用蒙特卡洛方法获取流场数据，详细描述了拐角区域干扰流场的主分离泡和次分离泡的精细结构。针对第2 类问题，转捩/湍流边界层导致干扰流场更加复杂。Holden 等［17-18］针对6°前锥湍流锥裙模型，在高马赫数Ma∞=11～16、高雷诺数Re∞≈106条件下开展了试验研究，通过纹影、全息等一系列手段测量了壁面压力、摩阻、热流信息，并与理论预测值进行对比，但没有详细评估各壁面量之间的关系。冈敦殿［19］改变半锥角和前锥长度，测试了Ma∞=3 条件下多个锥裙的上游流态，建立了激波与湍流边界层干扰流场，观察到拐角处的分离流动和下游大尺度结构，并获取5°～40°锥裙的时间相关纳米粒子示踪的平面激光散射图像，发现轴对称流场存在明显的周向运动，但没有对流动分离的非定常运动开展分析。Running等［20-21］对Ma∞=6 条件下7°前锥的锥裙结构开展风洞试验，根据上游边界层呈层流、转捩、湍流3 种状态，评估了头部钝度、裙角度、来流雷诺数等参数变化对边界层分离、再附的影响；他们还采用红外测热技术定量分析了热通量条纹的尺度和周向特征［22］，并利用高频响应的压敏漆技术成功捕捉到激波低频振荡现象［23］。Shiplyuk［24］、Bedarev等［25］对Ma∞=5.92 的7°～17°锥裙开展了试验和计算研究，验证了不同湍流模型对转捩/湍流情况下的压力分布和热载荷预测的准确度，Frayssinet等［26］进一步获取了该模型在1°攻角下的压力和热流分布，初步刻画了分离点位置沿迎风区向背风区的演化，但并未针对不同周向子午面的壁面量关系和流动分离情况进行分析。

现有高超声速锥裙研究主要采用风洞试验测量和雷诺平均模拟、蒙特卡洛方法等数值手段，但采用高精度数值模拟的研究极为少见。笔者前期已针对轴对称锥裙开展了国内首个激波/湍流边界层干扰直接数值模拟（Direct Numerical Simula⁃tion， DNS）研究［27］，但计算域仅局限于有限的周向范围并采用周期性边界条件。因此，基于周向平均结果的分析不可避免地忽视了三维横流效应的影响。与此不同的是，本文对锥裙整个360°周向进行直接数值模拟，研究了攻角对干扰区流动的影响规律，重点关注0°、90°、180°这3 个周向子午面的流场结构和壁面量，采用功率谱分析、本征正交分解方法研究干扰区分离泡非定常运动特性，并比对三维横流效应下再附边界层演化过程的差异。

1 直接数值模拟方法

1.1 计算模型和网格

本 文 计 算 模 型 与Running 等［20］在AFRL 的马赫6 路德维希管风洞试验中所采用的锥裙构型一致，由7°半锥角的前锥和34°裙结构组成，其长度分别为609 mm 和76 mm。图1 给出了计算域示意图，定义z为轴向，r为径向，φ为周向。将原点设置在前锥顶点处，记为z=0 mm。类似于Sivasubramanian 和Fasel［28］、Huang 等［29］对 尖 锥边界层转捩进行DNS 研究的处理，模拟区域不包含尖锥头部，而是将计算域入口设置在尖锥顶点下游z=156 mm 处。计算域出口位于裙结构的尾部。计算域流向长度为517 mm，法向高度为40 mm，周向角度为360°。为了使入口层流发生转捩，在壁面za=180～185 mm 范围设置定常吹吸扰动，参考Pirozzoli 等［30］的设置，随机法向速度扰动的形式表示为Vbs=Afbs（z）gbs（θ），其中扰动幅值A= 0.4U∞，空间函数分别定义为

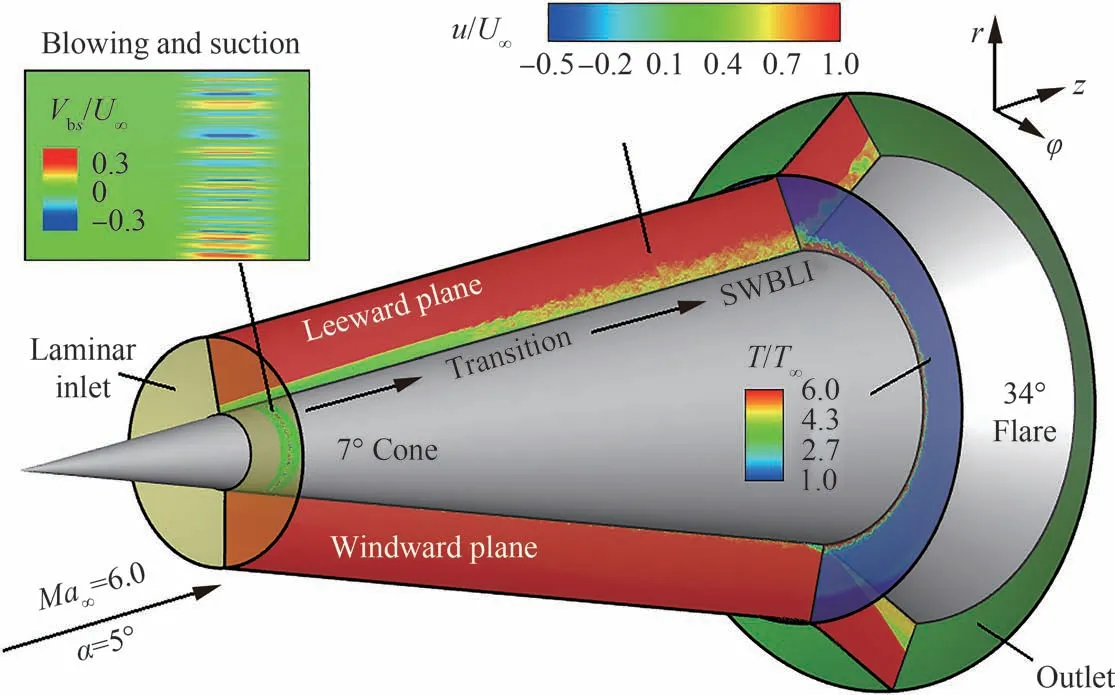
图1 计算域示意Fig.1 Sketch of computational domain

式中：Φl为0～1 的随机数；Lφ为周向计算域宽度；θ为周向角度。

图2 给出了计算网格的分布。定义x为壁面流向，y为壁面法向。图2（a）中流向-法向截面中网格间隔10 个点显示，沿壁面流向采用2 757 个网格点进行离散，其中上游转捩区156 mm＜z＜576 mm 逐渐加密地分布了1 301 个网格点，核心干扰区576 mm＜z＜660 mm 均匀分布了1 407个网格点，在缓冲区660 mm＜z＜675 mm 对出口附近网格进行拉伸，布置了逐渐稀疏的51 个网格点抑制激波反射干扰。沿壁面法向采用指数加密技术使y方向网格逐渐向壁面聚集，设置319 个网格点。所有周向子午面的网格均与此一致。图2（b）中法向-周向截面中网格间隔5 个点显示，为了在周向采用周期条件处理，周向1 201 个网格点分布在θ=−90°～269°的范围。在θ=−22.5°～205.5°的范围内均匀分布了1 000 个网格点，网格向周向边界逐渐变疏作为缓冲，分析取θ=0°～180°范围结果进行后处理。在核心干扰区，均匀的流向网格尺度为Δx=0.06 mm，周向网格对应角度为θ=0.225°，但周向网格尺度随流向锥裙半径增大而增大，例如在上游参考点zref=580 mm 的尺度为Δrθ=0.280 mm，拐角zc=609 mm 的尺度为Δrθ=0.294 mm，下游zd=660 mm 的尺度为Δrθ=0.427 mm。壁面法向首层网格厚度为Δyw=0.01 mm。表1 列出了θ=0°，90°，180°这3 个典型周向子午面的网格分辨率，上标“+”表示按照当地壁面参考量μτ、νw进行处理。本文中“平均”表示时间平均，对于变量η，可分解为η=ηˉ+η′和η=ῆ+η′′，其 中ηˉ为η的 雷 诺 平 均 值，为η的密度加权平均值，对应的脉动值分别表示为η′、η′。

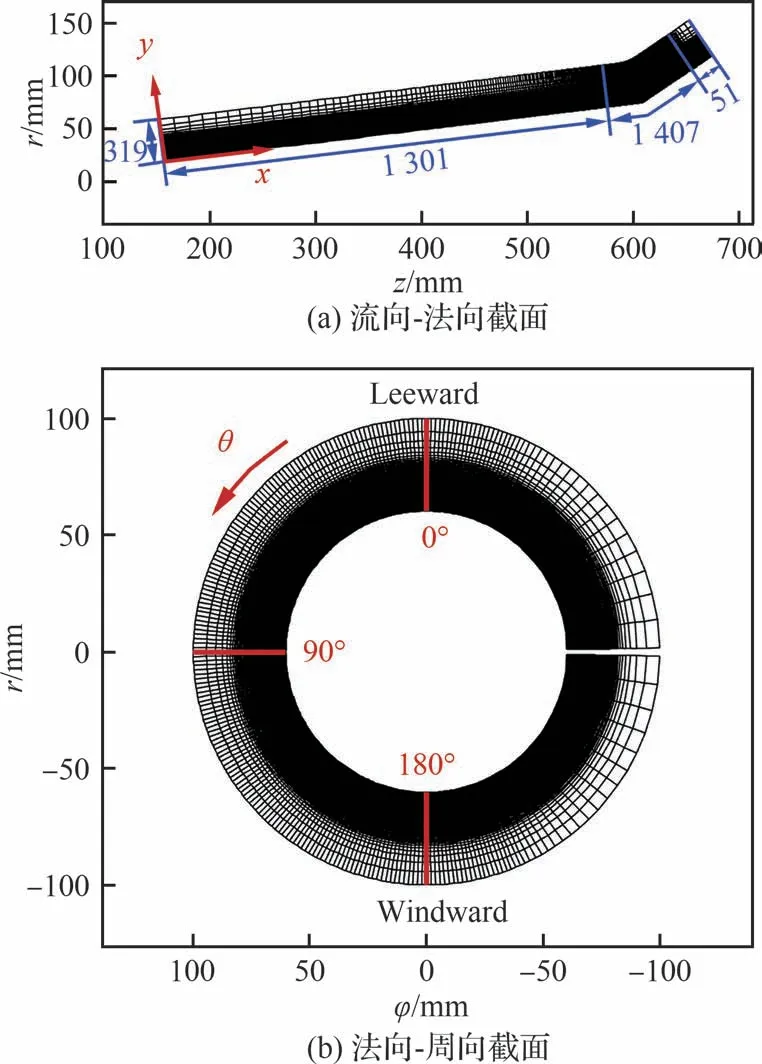
图2 网格分布Fig.2 Grid distribution

1.2 DNS 设置

采用高精度有限差分代码OpenCFD-SC，直接求解一般曲线坐标系下的完全气体三维守恒型可压缩Navier-Stokes 方程。该求解器已广泛应用于可压缩湍流计算，大量反射激波干扰和压缩拐角研究证实其在激波/边界层干扰问题计算精度和可靠性，对升力体、钝锥等复杂构型的计算也能够得到令人满意的结果。因此其模拟能力满足本文对锥裙结构的计算需求。采用来流参数对控制方程进行无量纲处理，参考长度为L=1 mm。黏性系数由Sutherland 公式计算，压力和温度关系满足无量纲理想气体状态方程，Prandtl 数、比热比分别为Pr=0.7、γ=1.4。计算条件如下：马赫数为Ma∞=6.0，单位雷诺数为Re∞=10 800 mm−1，静温为T∞=65 K。除非另做说明，下标“∞”和“w”分别表示来流、壁面量。由于大攻角会导致前锥背风区流动分离，而小攻角没有明显三维横流影响，为满足对锥裙拐角区域SWBLI 的研究需求，这里将攻角设为α=5°。

数值方法方面，空间对流项离散采用由Martín 和Taylor［31］、Wu 等［32］提 出 的 带 宽 优 化WENO-SYMBO 格式和限制器，黏性项由八阶中心差分格式处理。时间推进采用三阶总变差衰减的Runge-Kutta 方法，时间步长为ΔtU∞/L=0.005，U∞为来流速度。对于边界条件，计算域入口为层流边界层，层流边界层剖面是通过相同来流条件的三维层流尖锥模拟得到，图3 给出了层流入口的密度、流向速度、温度的分布云图。出口为超声速条件。计算域底部是模型壁面，为无滑移等温壁条件，壁面温度为Tw=296.4 K，与恢复温度Tr的比值为Tw/Tr= 0.62，视为冷壁面。图1 所示吹吸扰动区域设置定常吹吸扰动，以较大幅值ψ= 0.4U∞加速尖锥转捩过程。此外，上边界设置无反射条件［33］以抑制伪扰动的反射。周向边界设置为周期性条件。

图3 层流入口Fig.3 Laminar inlet

2 典型流场结构

图4 给出了瞬时速度和时均温度分布云图，图中-T为无量纲平均温度。图4（a）、图4（b）通过三维视图展示了前锥上游流场从有序到杂乱的过程，表明入口层流在吹吸扰动作用下发生了转捩。图4（c）、图4（d）为沿锥裙中心轴从前向后的6 个典型流向截面二维视图，第1 截面为入口层流状态；第2 截面在背风中心线附近存在“蘑菇状”结构，沿周向存在向两边分别发展了横流涡结构，即出现转捩过程；随着吹吸扰动的持续作用和边界层的进一步发展，第3、4 截面中流动结构逐渐破碎；经过锥裙拐角干扰区后，第5、6 截面中流动已完全混乱。注意到在锥裙拐角后出现了激波/边界层干扰典型现象，如图4（c）中存在大范围速度为负的流动分离区域，图4（d）中出现了靠近壁面的温度升高现象。

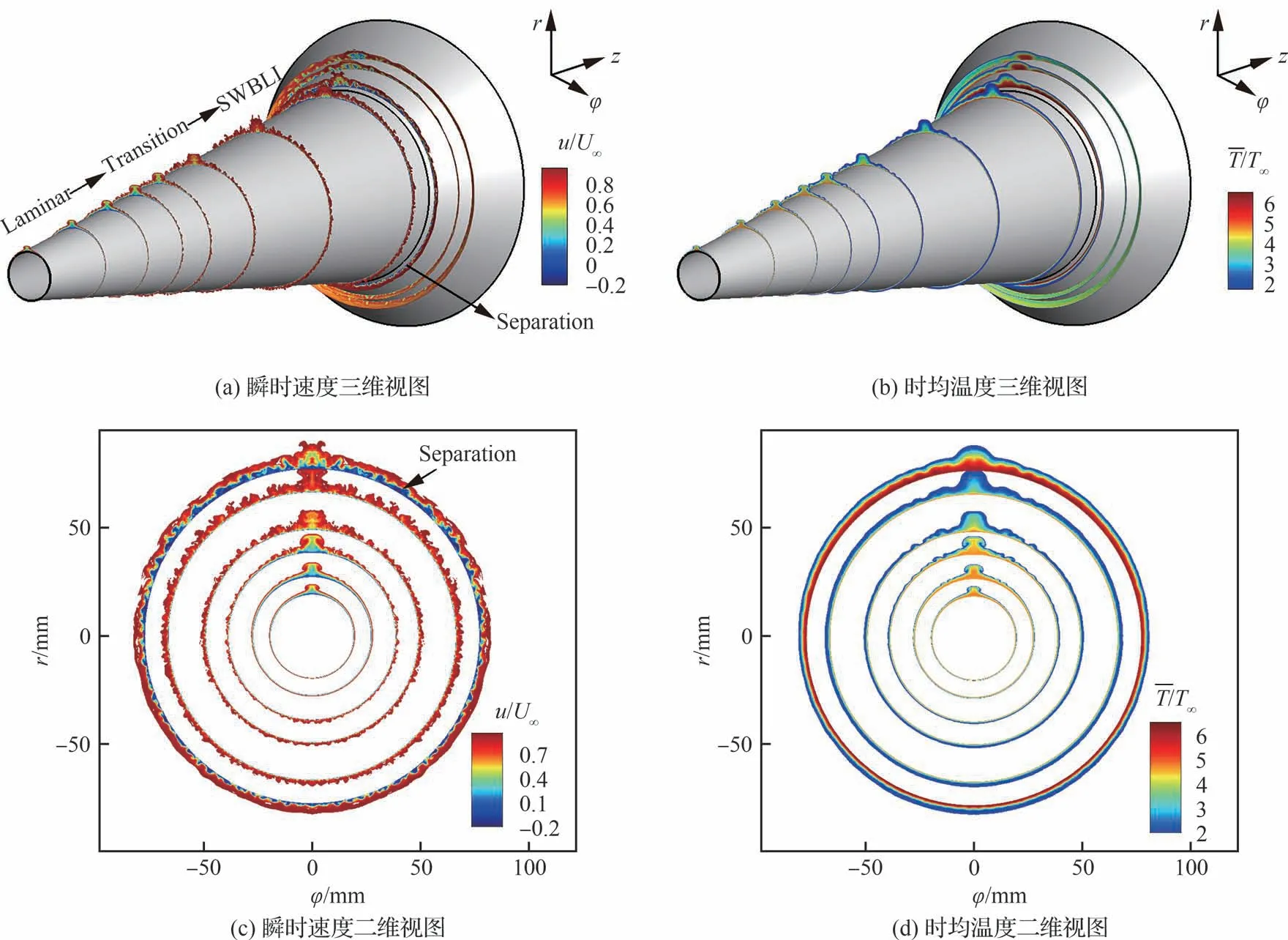
图4 瞬态和时均流场Fig.4 Instantaneous and time-averaged flowfield

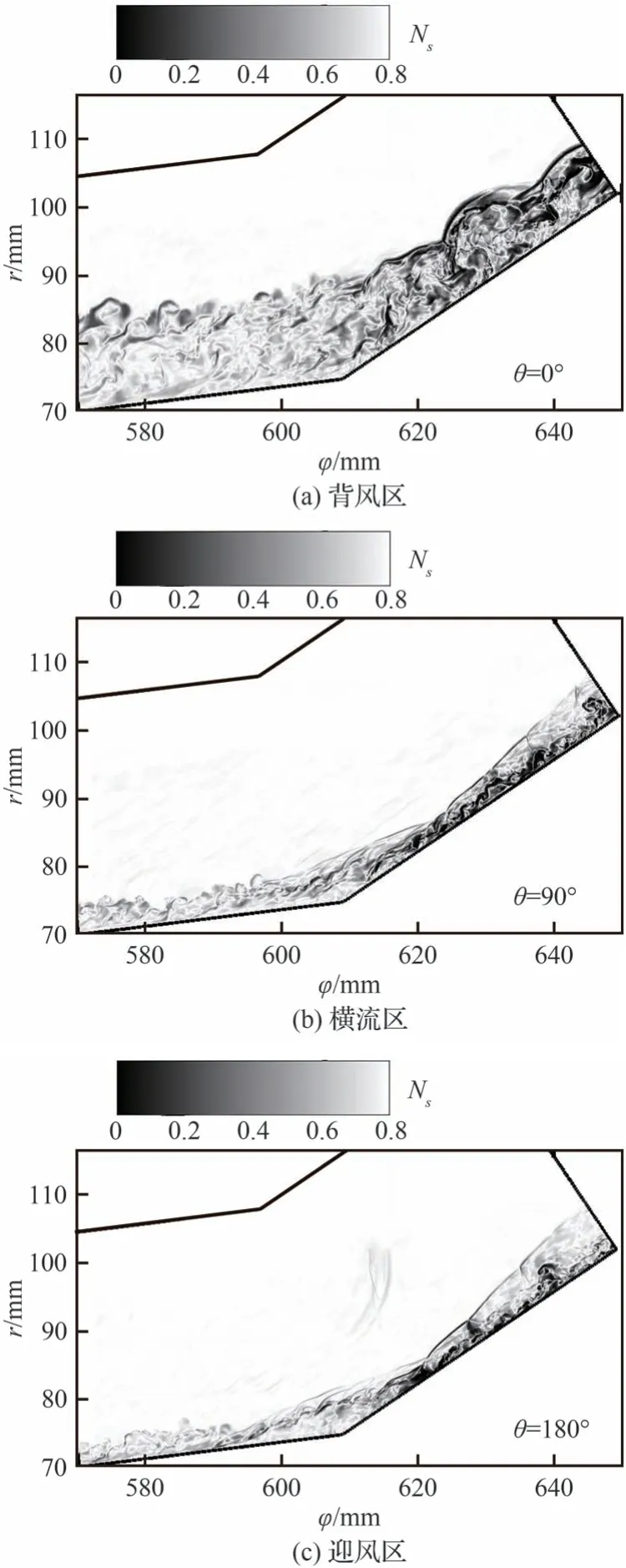
图5 典型周向子午面瞬时密度梯度场Fig.5 Instantaneous density gradient flowfield at typi⁃cal cross sections

存在攻角的情况下，图2（a）网格分布中所示的θ= 90°周向子午面中无黏流线与当地速度之间存在夹角，产生三维横流，其附近周向区域在后文分析中被称作横流区。几何上迎风中心线（θ= 180°）、背风中心线（θ= 0°）均与当地流线重合，附近周向区域分别被称作迎风区、背风区。通常利用99%来流速度位置判断边界层厚度，但这里存在压力梯度，因此以来流总焓的1.003 倍位置定义边界层厚度。经估算，迎风区、横流区、背风区在上游参考点处边界层厚度依次约为δref= 2.84， 3.63， 13.31 mm，表明边界层厚度从迎风区到背风区经历了逐渐增厚的发展过程。对比0°攻角锥裙相应位置边界层厚度（δref=5.88 mm），5°攻角下边界层的发展在迎风区、横流区被抑制，在背风区却大幅增厚。，其 中∇ρ为 密度梯度，下标“max”和“min”分别表示其最大、最小值，图中颜色越深的区域表明密度梯度越大。相较于Tong 等［27］对轴对称锥裙的研究，有攻角情况下激波强度变弱，并形成了更加复杂的相互作用波系。值得注意的是，背风中心线截面中难以辨识出规则的斜激波结构，这将导致背风区与其他周向区域的差异，其拐角处的流动分离可能主要由构型的变化导致，但未形成分离激波和再附激波。

3 平均壁面量分布

图6 给出了时间平均压力、摩阻和热流的壁面分布三维视图。沿流向观察到干扰导致的各壁面量显著增强现象。图6（a）中前锥的壁面压力水平远小于裙结构上的值，在锥裙拐角前已出现压力上升。在整个模型的干扰前后，压力从迎风区经横流区至背风区逐渐降低，在拐角前的压力剧增出现的位置逐渐后移。图6（b）中壁面摩阻在前锥上游部分保持在较低水平，其值升高表示转捩发生。经过拐角后进一步增大，但仅保持一小段流向距离随后降低。在攻角影响下，转捩位置在迎风面相对靠前（上游），经横流区至背风区向后（下游）推迟，但在背风中心线附近再次前移。整体来看，壁面摩阻在前锥上保持在较低水平，进入锥裙拐角干扰区后摩阻骤降为负，表示该位置发生流动分离，此后由于流动再附再次导致摩阻剧增，并持续到模型尾部。需要注意的是，图6（c）中壁面热流的流向峰值区域在周向存在明显的区别，迎风区的峰值更高。此外，背风中心线附近的分布与其他周向位置存在明显区别，可能与该区域的不对称小涡有关。

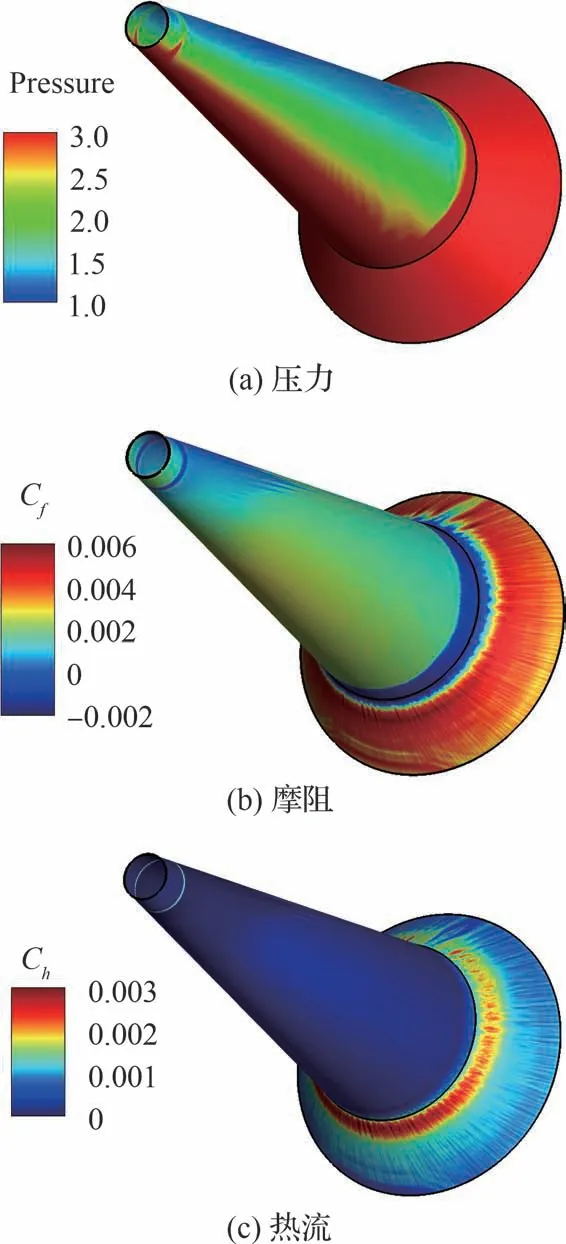
图6 时均壁面量分布Fig.6 Distribution of time-averaged wall quantities

图7 为3 个周向子午面中时均壁面压力Pw、摩阻Cf、热流Ch的流向分布。各壁面量在流动进入干扰区后都发生了一定程度的增加，但由于激波强度和边界层状态的不同，变化过程和定量程度在不同子午面上存在明显的差异。图7（a）中无量纲壁面压力在锥裙拐角之前缓慢上升，在下游再附区中随着周向位置变化存在不同变化趋势，其中迎风区和横流区的压力达到峰值（约上游的10 倍），此后略微降低并分别保持，但背风区的压力始终处于上升过程。整体来看，迎风区受到干扰最强，背风区受到的影响相对较小，横流区变化过程与0°攻角情况最为接近，无量纲壁面压力在上游约为0.037，经过干扰最终保持在0.49附近。

图7 典型周向子午面平均壁面量流向分布Fig.7 Streamwise distribution of time-averaged wall quantities at typical spanwise cross sections

图7（b）中壁面摩阻在干扰区降低，在分离区为负值，此后由于再附而剧增并达到峰值。以zref处的壁面量为参考，经过干扰区在背风、横流、迎风区再附边界层中摩阻最高增至原来的2.60、2.08、 1.72 倍（远低于0°攻角的4.72 倍左右）。从迎风区到横流区，以Cf＜ 0 定义的流向分离尺度（显著大于0°攻角的4 mm 左右）逐渐增大，从23.7 mm 扩大至26.3 mm，但背风中心线处流向分离区域仅11.8 mm，这是由于背风区近壁分离泡可能并不与从迎风面发展的分离泡相连。图7（c）中壁面热流在流动分离处略低，然后缓慢增加，在拐角处剧增并在再附点附近达到峰值（约为上游的5 倍），此后逐渐降低但始终高于上游，各子午面上相对大小与上游一致。该现象不同于0°攻角情况，热流在轴对称锥裙拐角处剧增后经历了非常缓慢的下降过程。

以上壁面量流向分布特征表明，热流的变化与压力和摩阻均存在一定的关系，与流动分离/再附、拐角构型变化相关。因此，图8、图9 分别给出了QP85 关系式［34］和雷诺比拟因子［35］在各子午面上沿流向的分布。图中，S 为分离点，C 为锥裙拐点，R 为再附点，下标0、90、180 表示图2（b）所示的周向位置对应角度。

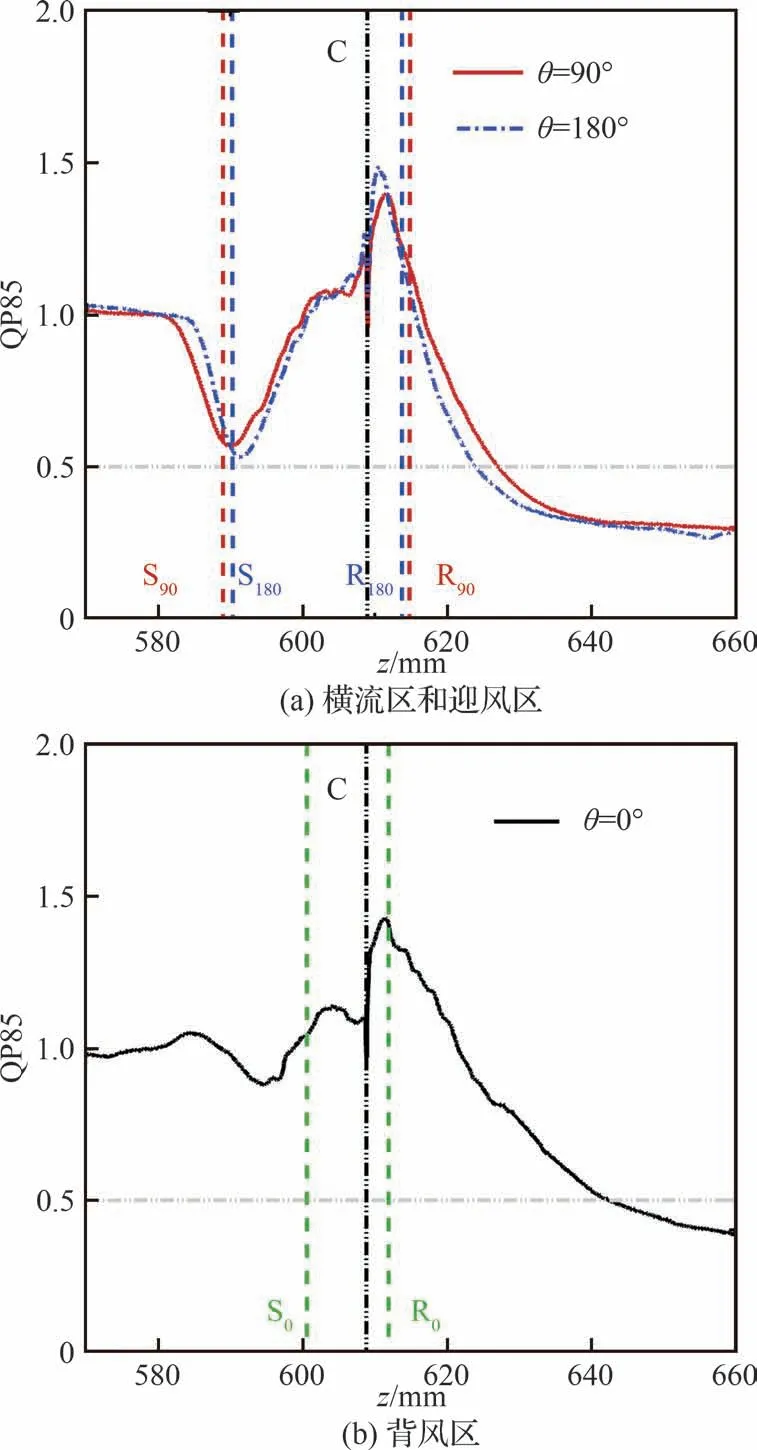
图8 QP85 流向分布Fig.8 Streamwise distribution of QP85

图9 雷诺比拟因子流向分布Fig.9 Streamwise distribution of RAF

平均热流与压力关系定义为

式中：下标“0”表示上游参考值。

如图8 所示，各周向子午面中上游基本满足QP85 ≈ 1.0，与Murray 等［36］的 试 验 结 果 一 致。流动分离和锥裙拐角构型的变化诱发了2 次QP85 上升，在0.5～1.5 之间变化；随后流动再附导致QP85 迅速降低，图8（a）中迎风区和横流区下游保持在0.3 左右。以上变化趋势在图8（b）的背风区中涉及的流场范围更大，直到下游区域仍处于下降状态。再附区的单调递减趋势与Priebe和Martín［37］在高超声速压缩拐角中的现象一致，与图7（a）中压力的持续上升有关。

平均热流与摩阻的雷诺比拟关系定义为

4 分离泡非定常特性

由图9 可知，RAF 在分离区完全失效，这是由分离区存在极小负值的摩阻所致。而图9（a）中，RAF 在迎风区、横流区的无干扰上游、下游恢复区均符合较好，其中上游RAF ≈ 1.07，与0°攻角 锥 裙 的 结 果 一 致，也 符 合Roy 和Blottner［35］在高超声速零压梯度边界层中给出的0.9～1.3 范围。下游则稳定在RAF≈1.20，在流向尾部出现小幅振荡，与0°攻角下逐渐增大的变化趋势略有不同。RAF 在图9（b）的背风区上游、下游都高于其他位置情况，上升、下降趋势所涉及的流向范围更广，说明其干扰存在明显不同。由此可知，在三维横流影响下，迎风区、横流区的无干扰上游、下游恢复区仍然可用QP85、RAF 对压力、摩阻、热流进行预测和评估。

根据在图4 观察到的流动分离现象，图10 进一步提取θ=0°， 90°， 180°这3 个周向子午面内锥裙拐角附近的干扰流场。在图10（a）～图10（c）给出的瞬态速度场（以来流速度U∞对瞬时速度u进行无量纲处理）中，将贴体流向速度小于0 的区域看作分离泡，用粉色点划线表示时均分离泡边缘，发现背风子午面的流动分离区域相对较小，但速度变化的法向范围相对最大。

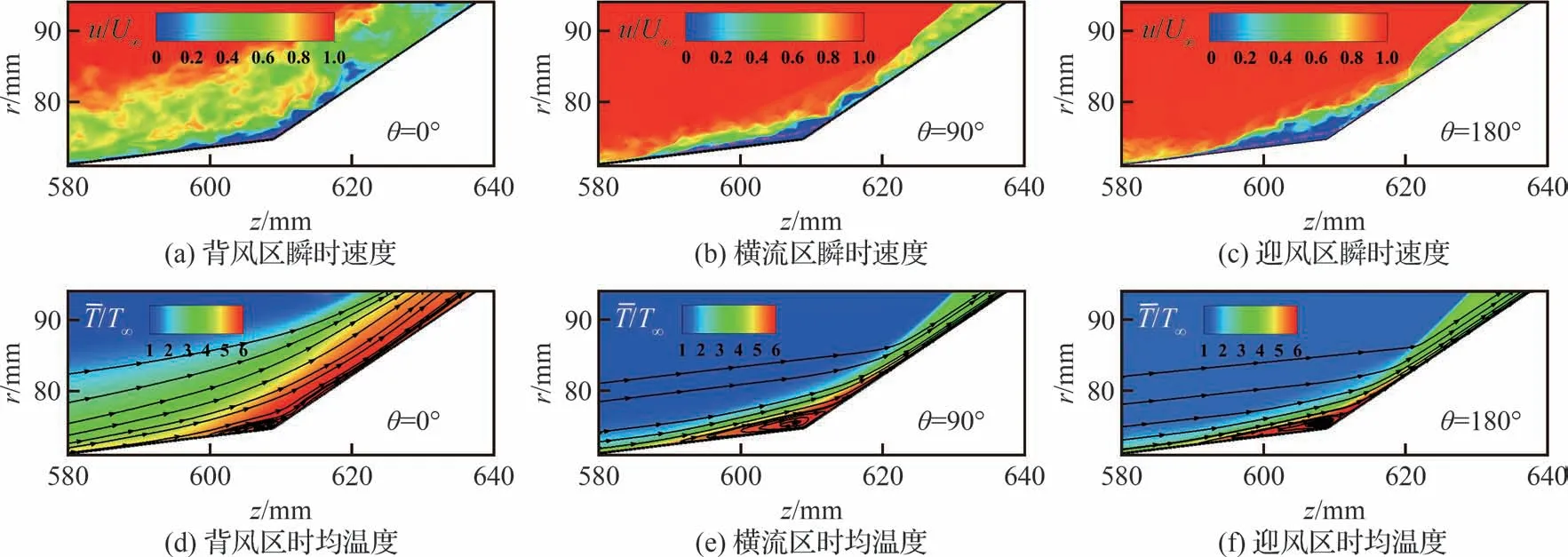
图10 典型周向子午面的流动分离Fig.10 Flow separation at typical spanwise cross sections

图10（d）～图10（f）的时均温度场（以来流温度T∞对时均速度-T进行无量纲处理）中叠加绘制了黑色流线。各子午面均出现流向较长、法向较短的分离泡结构，且温度较高的区域与回流区范围一致。然而，从迎风区经横流区到背风区，温度变化的法向范围逐渐变大，尤其是在背风子午面中该范围远超回流区，推测这与从迎风区到背风区逐渐增大的边界层厚度有关。注意到流线表征的回流区中，背风子午面的分离泡较为分散，而横流区、迎风区表现为一个较为整体的分离泡。这可能是由于在攻角影响下，背风区结构不完全对称，且背风中心线附近的近壁涡与其他周向位置不同的缘故。

图7（b）给出的壁面摩阻流向分布、图10（d）～图10（f）所示平均流线趋势明确揭示了锥裙拐角区域干扰流场的流动分离现象。通过提取干扰区中贴体流向速度小于0 区域，对分离泡面积进行统计，图11 给出了以其最大值进行无量纲处理的面积脉动A′（t）随时间的变化历程，观察到分离泡在不断进行膨胀和收缩运动。图10（a）～图10（c）所示瞬态速度场中，贴体流向速度的负值范围在平均分离泡边缘之外，表明该时刻的分离泡正处于膨胀运动。图11 绘制了以最大值进行无量纲处理的平均分离点S 位置的壁面压力脉动随时间t的变化历程。

图11 分离泡面积脉动平均分离点压力脉动时间序列Fig.11 Time series of separation bubble area fluctuation and pressure fluctuation at mean separation point

为了进一步揭示干扰区流动分离与激波之间的关系，图12 给出了分离泡面积脉动A′（t）与平均分离点S 的壁面压力脉动p′w( )t之间的相关性系数CPA结果，其定义为

图12 分离泡面积和平均分离点压力的互相关系数Fig.12 Cross-correlation coefficient between separation bubble area and wall pressure at mean separation point

式中：Δt为时间间隔，横流区子午面在Δt= 0 处达到峰值CPA≈ 0.45，即干扰区的激波低频振荡与分离泡的非定常运动密切相关。迎风区子午面中两者也具有强相关性，但观察到一定的时间延迟。而背风区子午面中两者无关，这是由于其激波结构不明显，因而流态区别较大。

图13 给出了θ= 0°， 90°， 180° 3 个周向子午面上分离泡面积序列的预乘功率谱，进一步对干扰区频域特征开展分析，其中，ω为角频率，Φ（ω）为功率谱。这里采用了Welch 方法和Hamming窗，将数据分为4 段，重叠率设置为50%。Strou⁃hal 数定义为St=fL/U∞，其中f为频率。显然，各子午面上分离泡面积脉动的主频均为St=0.009 7，背风区还在St= 0.029 存在局部峰值，可能与图10（d）中观察到回流区的分散的多泡结构相关。

图13 分离泡面积脉动预乘功率谱Fig.13 Pre-multiplied spectra of separation bubble area fluctuation

根据图11 中给出的各周向子午面上平均分离点位置的压力时间序列，图14 给出其预乘功率谱，并以脉动均方根的平方进行处理，同时给出zref的结果作为参考。各子午面的上游压力脉动主频均在高频区，即背风区、横流区、迎风区中zref站位的压力脉动主频分别为St=0.22，0.45，0.71。从干扰区站位S 结果来看，各子午面预乘谱与上游的分布趋势相似，全局主频略微向低频区移动，分别降至St=0.14，0.25，0.35。重要的是，在迎风区、横流区，分离点S 的预乘功率谱均在低频区St=0.009 7 处存在局部峰值，该频率与图13 中分离泡面积脉动的主频一致，相应时间尺度分别为上游的73.2、46.4 倍。与以往SWBLI 研究中典型的时间尺度在上游的10～100 倍之间的分离激波低频振荡现象相符。

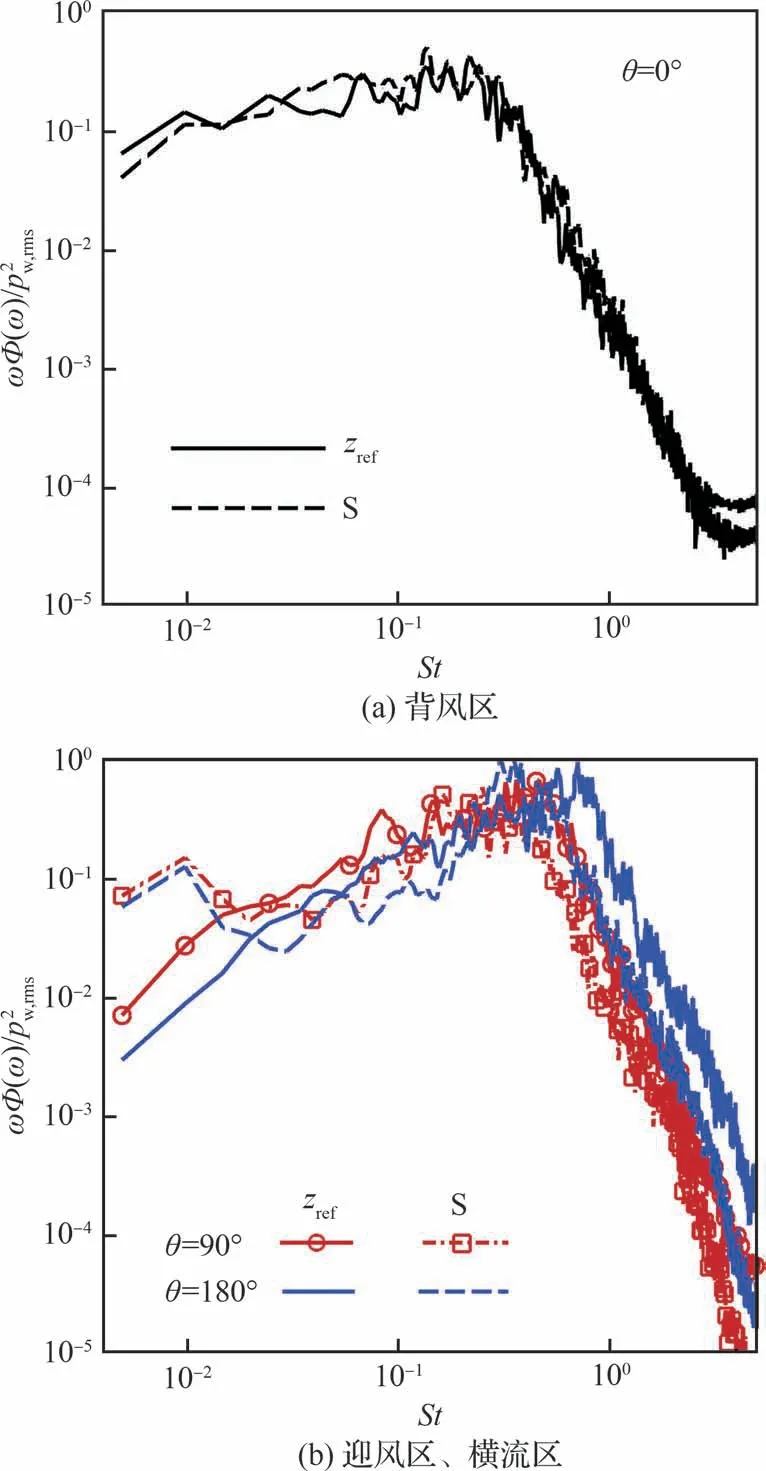
图14 平均分离点壁面压力脉动预乘功率谱Fig.14 Pre-multiplied spectra of wall pressure fluctua⁃tion at mean separation point

对图15 的预乘功率谱结果按照

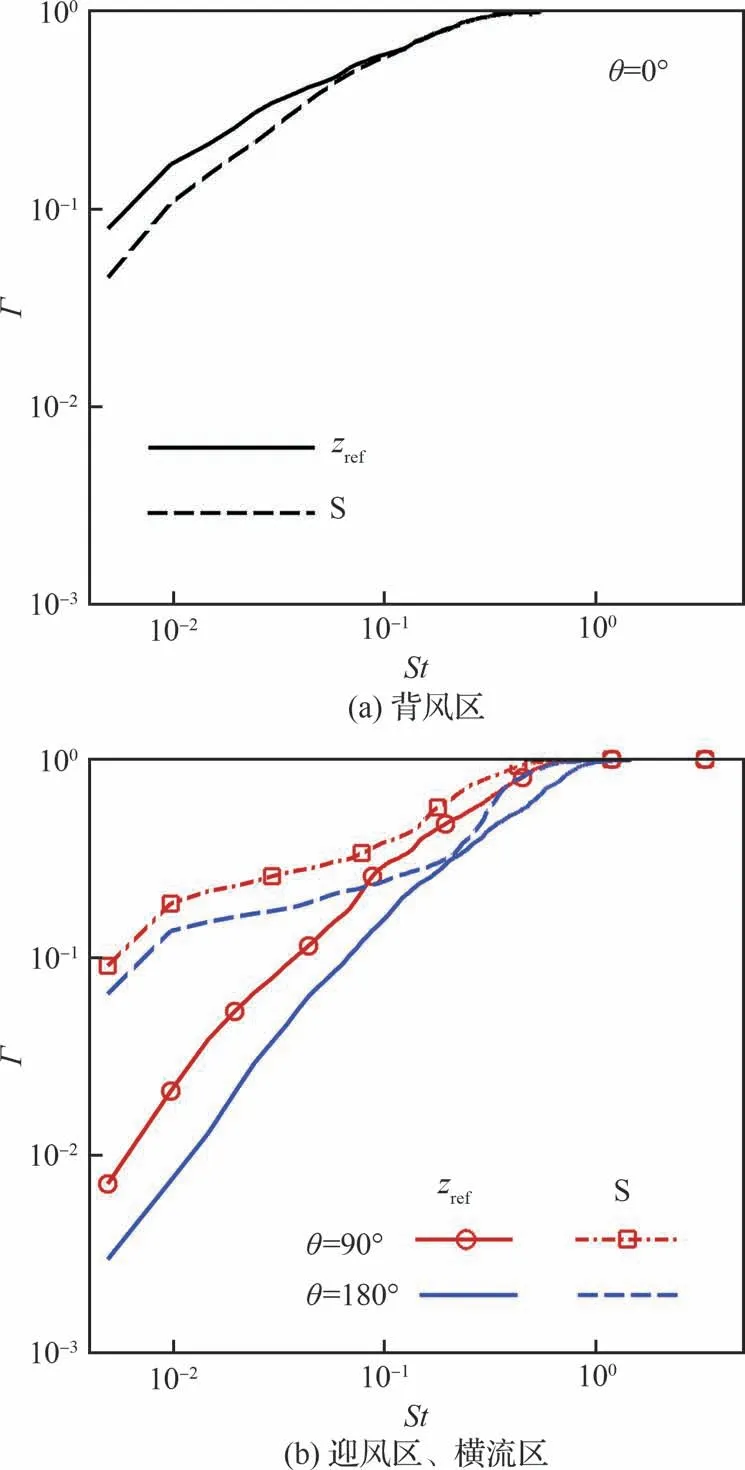
图15 平均分离点壁面压力脉动预乘功率谱积分Fig.15 Integral of the pre-multiplied spectra of wall pressure fluctuation

进行积分并采用频率最大值结果归一化处理，得到各频率能量分布。将St＜ 0.01 定义为低频区，图15（a）的背风区中，上游和分离点S 的低频段能量占比分别为17.3%、11.0%。而图15（b）中迎风区、横流区则出现完全相反的结果，分离点S 的低频能量占比剧增。具体而言，分别从参考点处的0.8%、2.4% 增至分离点S 处的13.5%、19.0%。因此，频域分析结果进一步确定了迎风区、横流区分离激波的低频特征，但是背风区不存在明显的激波结构（见图5（a）），因此仅观察到分离点S 处压力脉动与上游一致的高频特征。

为了进一步揭示分离泡非定常运动中的典型相干结构，采用本征正交分解（Proper Orthogonal Decomposition， POD）对 流 向574 mm ＜z＜625 mm、法向约0 mm＜r＜15 mm 采样窗口区的瞬态流向速度场进行分析。采样时间步长ΔtU∞/L= 0.4，共获取N= 2 500 个POD 模态。图16 给出了模态能量Ek分布和累积能量占比。图16（a）表明Ek随着模态阶数k的增加而逐渐降低，例如第10、100 阶模态的能量分别比第1 阶模态下降约1、2 个数量级。图16（b）给出的累积能量揭示第1 阶模态能量占比最高，约20%左右，视作主能量模态。注意到各子午面的能量变化趋势虽然没有显著差异，但图16（a）表明背风区能量在低阶模态中相对最低，而在高阶模态中相对最高。图16（b）证实了上述规律，背风区的累积能量在前100 阶模态都是相对最低的。

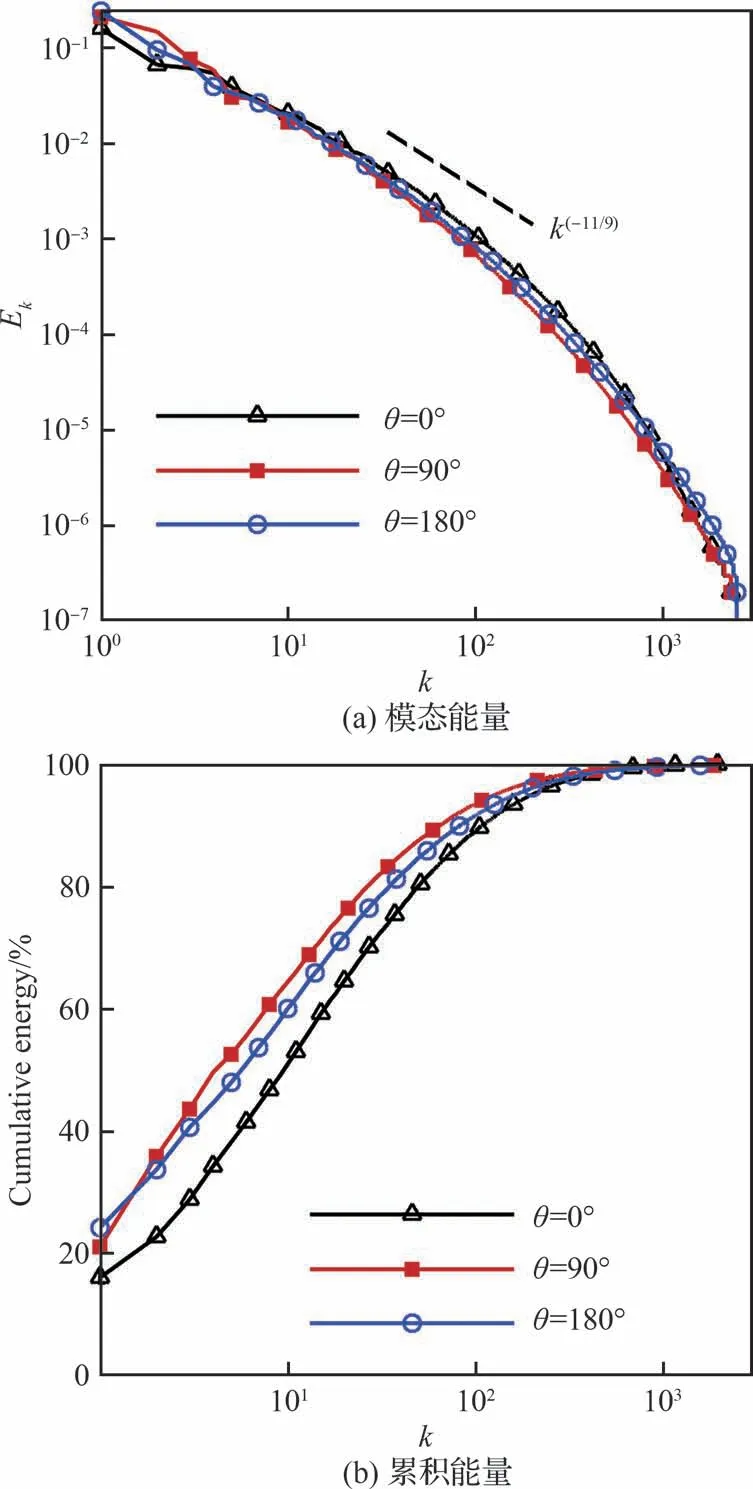
图16 POD 模态能量分布Fig.16 Energy distribution of POD modes

POD 模态时间系数ak（t）反映了采样窗口区干扰流场的非定常特征。图17（a）中ak（t）预乘功率谱云图表明，占优频率随着模态阶数增加从低频区迅速转向高频区，在k＜100 都低于上游压力脉动主频。具体而言，k＜5 低阶模态的峰值频率集中在低频范围，在分离泡面积脉动特征频率附近，但横流区主能量模态主频略有升高。5 ＜k＜10 的迎风区峰值频率也略有升高。图17（b）为ak（t）和分离泡面积脉动的相关系数CMA随模态阶数的变化，定义为

图17 模态时间系数的预乘功率谱和互相关系数Fig.17 Pre-multiplied spectra and cross-corre-lation coefficient of time coefficient of POD modes

整体来看，主能量模态均与分离泡具有较高的相关性，此后低阶模态相关性随阶数增大而急剧衰减，高阶模态的CMA维持在零附近。因此，分离泡低频膨胀/收缩运动仅与主能量模态和第2阶模态（迎风区）密切相关，这与在反射激波干扰问题中得到的POD 分析结果存在显著区别，以往分析得到的分离泡呼吸与前10 阶POD 模态都存在显著的相关性。

图18 给出了第1、2 阶POD 模态在部分法向范围的空间分布，并叠加显示了平均分离线位置。各子午面中，主能量模态均对应靠近壁面的大尺度含能结构，出现在流动分离剪切层附近。第2 阶模态的主要结构分布范围基本没有变化，但表现流向尺度减小并具有正负交替特征的多个结构。对比不同周向子午面来看，从迎风区到背风区，主要空间结构的法向范围逐渐扩大，与逐渐增厚的边界层变化相关。

图18 POD 模态空间分布Fig.18 Spatial distribution of POD modes

选取前10 个低阶POD 模态对干扰区速度场进行重构，图19 给出了由分离泡面积最大值Amax进行无量纲处理的分离泡面积A时间序列。对比来看，POD 重构曲线与DNS 原始曲线吻合较好，重构的面积变化准确捕捉了分离泡膨胀、收缩运动的交替变化过程。评估重构精度均达到87%以上，证明低阶模态在该区域占主导地位，与以往在反射激波干扰、压缩拐角等研究中得到的结论类似。两者之间存在的微小差异体现在局部高频脉动部分，这是由于缺少高阶模态的高频区能量所导致的。

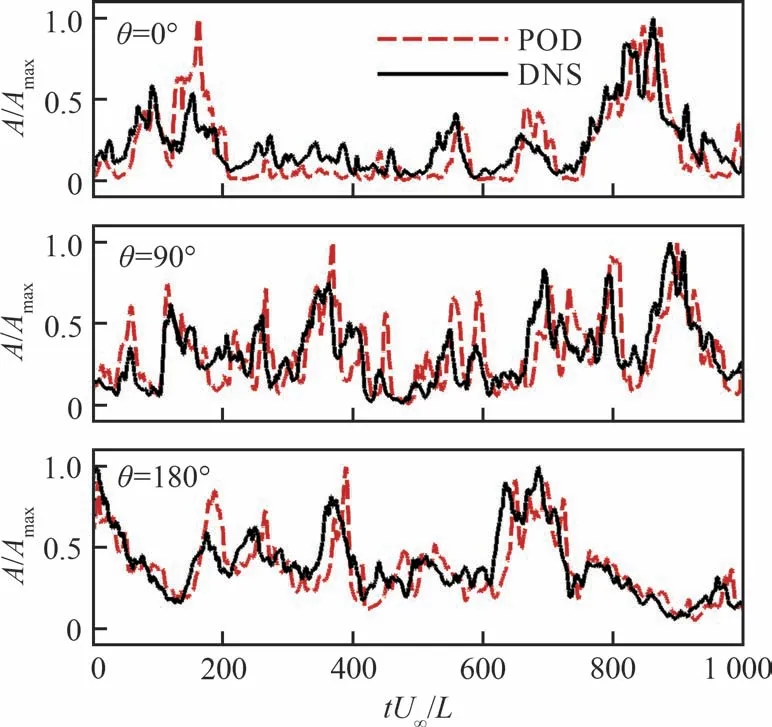
图19 分离泡面积时间序列的重构Fig.19 Reconstruction of time series of separation bubble area

5 再附边界层演化

为了更好地理解再附边界层的恢复过程，进一步刻画时均速度、温度、湍动能、雷诺应力分量及其各向异性不变量等特征统计量的流向演化，并通过对比θ=0°，90°，180°这3 个周向子午面的异同评估三维横流效应对干扰恢复过程的影响。所选取的流向站位分别记为R1～R5，相应流向坐标依次为z=610，617，626，635，650 mm。其中R1 位于分离泡内，R2 位于再附点后，R3～R5均位于下游再附边界层中，同时给出了各子午面上游zref站位的结果作为参考。

图20 为壁面贴体流向速度和温度的法向分布，图中yn为距离壁面的距离。经过干扰，速度沿流向先减小然后逐渐增大恢复，而温度沿流向先升高再逐渐降低恢复。上述过程在迎风区、横流区子午面比在背风区子午面更迅速。具体而言，图20（a）～图20（c）中背风区的上游速度剖面发生变形，与迎风区、横流区较为饱满的速度剖面存在显著差异。R1 出现负速度，这与其存在于回流区的情况是对应的，R2 位于再附点下游不远处，近壁区受到的干扰较大，R3、R4 在非常近壁区迅速接近于上游情况。但在相对外层区域，横流区的R3～R5 存在2 段速度分别在0.80U∞、0.85U∞的稳定区域。各子午面中R1～R5 的法向分布都没有与zref达到一致，而在0°攻角下边界层外缘基本可以恢复到与来流一致的水平。图20（d）～图20（f）中温度变化趋势与图20（a）～图20（c）是类似的，R1、R2 受到干扰影响温度出现明显的升高，在内层大幅度偏离，在外层逐渐靠近上游参考值。虽然R3～R5 站位在横流区、迎风区的近壁区已开始恢复，且边界层外缘的分布基本与上游剖面重合，但背风区的整体恢复相对较慢，直到R5 站位还保持着显著的温度升高。

图20 流向速度和温度法向分布的演化Fig.20 Evolution of normal distribution of time-averaged streamwise velocity and temperature

将湍动能k进行无量纲处理为

式中：密度ρ、摩擦速度uτ均采用当地参数。

图21 给出了各子午面内的法向分布。由于5°攻角带来三维横流和周向梯度变化，各子午面在zref站位存在明显不同。整体来看，迎风区、横流区、背风区的全局峰值分别为k+=6.43，7.31， 13.43，高于0°攻角下的k+= 5.2。其法向位置出现在内层y+n≈ 20～30，略高于Pirozzoli 和Grasso［6］在零压力梯度可压缩湍流边界层中给出的y+n≈ 14。外层y+

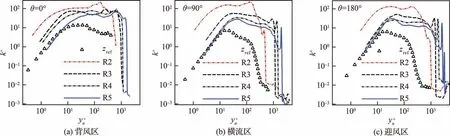
图21 湍动能法向分布Fig.21 Normal distribution of TKE

n≈ 200 附近还出现了局部峰值。湍动能在背风区外层仍然较高，而迎风区、横流区法向分布规律与以往结果一致。激波干扰对下游区域的影响主要体现在2 个方面。首先是湍动能被增强，R2～R5 站位的湍动能法向分布曲线整体抬升，在R2 外层峰值偏离上游最多，在R3、R4 中降低并形成平台区域，而在下游R5 的近壁区已出现与上游重合的部分，外层区域还存在较大差异。其次，干扰导致峰值的法向位置发生变化。各子午面的R2 峰值位置均移向外层，攻角影响下R3～R5 的背风区峰值始终在外层，而迎风区和横流区峰值已回到内层。根据图5 给出的瞬时密度梯度场可知，y+n～1 000 的小尖峰是激波导致的。背风区的激波影响明显较弱，而迎风区R5 站位的小尖峰不止一个，体现了复杂波系中存在多个压缩波相互作用。

图22 给出了雷诺应力流向分量u′′u′′、法向分量v′′v′′的法向分布，图23 给出了雷诺应力展向分量w′′w′′、剪切分量u′′v′′的法向分布，各分量均采用当地摩擦速度uτ进行处理。由于R1 位于分离点内，这里主要关注再附边界层中R2～R5 站位的变化特征，图中还给出了上游参考位置zref的结果以作对比。注意y+n～1 000 附近出现的尖峰现象表明外层区域明显受到锥裙拐角干扰区产生的激波结果影响。

图22 雷诺应力流向、法向分量的法向分布Fig.22 Normal distribution of streamwise and normal components of Reynolds stress

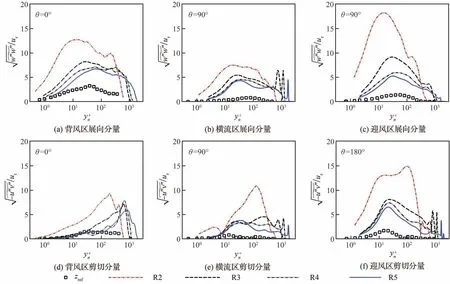
图23 雷诺应力展向、剪切分量的法向分布Fig.23 Normal distribution of spanwise and shear components of Reynolds stress

显而易见，经过干扰后各分量均被增强，这与Fang 等［10］在Ma∞=2.25 的入射激波平板中和Loginov 等［38］在Ma∞=2.95 的 压 缩 拐 角 构 型 上的现象一致。相对于上游参考值定义雷诺应力分量的放大因子，攻角的存在导致了再附点附近放大因子剧增。具体而言，0°攻角再附点附近（R1）4 个分量（u″u″、v″v″、w″w″、u″v″）的放大因子分别为3.0、16.0、9.0、17.0，而5°攻角下再附点附近（R2）在迎风子午面分别为3.95、22.19、12.79、8.48。对 比 图23（a）～图23（c）、图23（d）～图23（f），法向分量增大的倍数大于流向分量。与Schreyer 等［39］在高超声速激波边界层干扰中发现的法向脉动比流向脉动的放大更为显著的结论类似。另一个重要现象是峰值位置显著外移。以流向分量为例，在迎风区上游zref站位，沿壁面法向逐渐增大，在y+n=18.05 达到峰值，然后逐渐减小，该趋势与以往文献结果一致，但峰值出现的位置相较于Pirozzoli 等［40］在可压缩湍流边界层中得到的峰值位置y+n=13 略远离壁面。经过干扰，再附点附近R2 站位的全局峰值出现在显著远离壁面的位置，达到～100 量级，而原峰值位置在～10 量级保持并形成局部峰值。

在不同周向子午面内，雷诺应力分量的增强和峰值外移的基本特征没有发生本质上的改变。但是，相对于迎风区，横流区法向分量的放大因子有所降低，峰值位置也更加远离壁面。背风区情况则非常不同，三维横流效应对背风子午面各分量的外层影响最大，导致其峰值位置沿R1～R5 持续外移；尤其是对于包含法向速度脉动的法向分量和剪切分量，一方面，在横流和迎风子午面中近壁区域存在全局或局部的峰值，而背风子午面内完全不存在内层峰值；另一方面，横流、迎风子午面中放大因子沿R3～R5 呈逐渐降低的恢复趋势，而背风子午面内则存在波动。最后，从干扰恢复过程来看，沿再附边界层向下游发展，R3～R5 的峰值位置逐渐靠近壁面。R2～R5 的峰值放大因子逐渐降低，内层分布逐渐靠近上游参考值，表明再附剪切层逐渐衰减，近壁结构逐渐恢复。相较于0°攻角流向分量恢复最慢的特征，5°攻角下各子午面内流向分量的恢复却是最为迅速，表明攻角导致的三维横流对法向、周向速度脉动的影响强于流向速度脉动。内层恢复比外层快，直到下游R5 位置，雷诺应力各分量在所选取的周向子午面上均未完全恢复，尤其是背风区子午面中与其上游分布差异较大。

图24 进一步给出下游R5 站位处雷诺应力张量各向异性不变量的法向分布情况，根据Lum⁃ley［41］给出的三角形辅助线以观察湍流状态变化，IIIb、IIb分别为雷诺应力各向异性张量第三、第二不变量。图中的3 个顶点分别标注为一组分（One-Component， 1C）、两组分轴对称 （Two-Component Axisymmetric， 2CA）和 各 向 同 性（Isotropic， ISO）状态，3 个边界分别标注为轴对称压缩（Axisymmetric Compression， AC）、轴对称膨胀（Axisymmetric Expansion， AE）和两组分（One-Component， 2C）状态。对比图中3 个典型周向子午面情况，发现近壁区的湍流都呈2C 状态，并很快达到各向异性峰值，与可压缩湍流边界层的近壁状态一致，但是从迎风面到背风面各向异性的程度逐渐降低。随着法向位置增大，湍流各向异性减弱，折返向AC 状态靠近，但横流区更接近AE 状态，而迎风区、背风区更靠近2C 状态。此外，随着法向位置进一步增大，湍流状态再次出现反转，然后沿着AE 状态发展，由于尚未完全从激波干扰中恢复，仅在横流区子午面观察到比较接近ISO 的状态。

图24 R5 站位湍流状态法向演化Fig.24 Evolution of normal distribution of turbulent states at location R5

6 结 论

对高超声速下有攻角锥裙的激波/边界层干扰问题进行直接数值模拟研究，通过对比背风区、横流区、迎风区3 个周向子午面的典型流场结构、分离泡非定常运动特性、下游再附边界层演化过程，得到以下主要结论：

1） 激波/边界层干扰导致壁面压力、摩阻和热流显著升高，分别达到上游的10、2、5 倍左右。热流与压力在上游满足QP85 ≈ 1.0 关系式，在干扰区由分离、拐角构型变化诱发2 次上升，再附后迅速降低。热流与摩阻的RAF 关系式在分离区完全失效，在迎风区、横流区的无干扰上游、恢复区下游均符合较好。

2） 各周向子午面内均出现流动分离现象，分离泡面积脉动主频均为St≈ 0.009 7，采用低阶POD 模态重构干扰流场，表明分离泡非定常运动的低频特征。在三维横流影响下，平均分离点压力脉动在迎风区和横流区的低频段增强，对应时间尺度分别为上游的73.2、46.4 倍，表明激波低频振荡与分离泡膨胀/收缩运动密切相关，而在背风区两者无关。

3） 再附边界层演化研究结果表明，干扰后速度、温度、湍动能在近壁区迅速恢复，但外层由于恢复较慢，攻角的存在导致再附点附近雷诺应力分量放大因子剧增，流向分量恢复最迅速。三维横流效应影响主要体现在背风区，雷诺应力各分量峰值位置持续外移，下游近壁区的各向异性峰值减弱，湍流边界层仍在恢复中。