Online Consensus Control of Nonlinear Affine Systems From Disturbed Data

Yifei Li , Wenjie Liu , Jian Sun , Chen Chen ,Jia Zhang , and Gang Wang

Dear Editor,

In this letter, we introduce a novel online distributed data-driven robust control approach for learning controllers of unknown nonlinear multi-agent systems (MASs) using state-dependent representations.The proposed method is formulated as an online optimization problem, based on finite-length disturbed data and expressed in terms of linear matrix inequalities (LMIs), whose solution at each time step yields a stabilizing controller for each agent.The feasibility of the optimization problem ensures the stability of the closed-loop system.

In recent years, the control community has shown significant interest in the distributed control of MASs, driven by their diverse range of applications in different fields such as physics, social sciences,biology, and engineering, as highlighted in [1]-[5].Direct datadriven control, inspired by the Willemset al.[6] fundamental lemma,has gained recurring attention.This approach offers advantages over model-based control, such as avoiding challenges related to model inaccuracies and high computational costs of system identification.As this field has rapidly and continuously developed, data-driven techniques for controlling different systems, albeit complex and nonlinear, have become relatively mature ranging from explicit state feedback control in [7] to model-predictive control in [8].

However, one of the main challenges in data-driven control is building a data-based system representation from disturbed data, as disturbances can undermine the condition of persistency of excitation required by the fundamental lemma.The S-lemma was introduced in [9] as a general framework for handling disturbances and has been widely used in e.g., [10]-[12].Nonetheless, they assumed that disturbances are only present in the offline data collection process but not during online operation.Recent work [13] has proposed data-driven robust control strategies that consider disturbed data during both learning and closed-loop operation, while ensuring stability and performance.However, these strategies are mainly limited to linear systems, and deriving solutions for nonlinear systems remain

s challenging.On the other hand, data-driven techniques based on sum-of-squares (SoS) optimization have been developed for polynomial systems [14], but they are computationally expensive.Moreover, while previous research has focused on centralized settings for single systems, the distributed setting for MASs subject to both offline and online disturbances is particularly unexplored.

To address these challenges, we propose a novel online distributed data-driven robust control method for the consensus problem of unknown nonlinear MASs.Our method builds upon the combination of the matrix S-lemma in [9] and the state-dependent representations in [15], to synthesize a state-feedback consensus control protocol by solving an online data-based optimization problem, in the form of LMIs, for each agent at each time step, while simultaneously providing stability guarantees.The main contributions of this work lie in threefold.1) The proposed method is not limited to rational nonlinearities and simplifies the computational complexity by establishing low-dimensional LMIs, making it comparable to the linear case;2) An online distributed method for designing the controller for each agent using disturbed data is advocated, which possesses a significantly improved robustness; and 3) Under standard conditions on both offline and online disturbances, uniformly ultimately bounded(UUB) of the closed-loop system is established for the proposed data-driven robust controller.

Problem statement: Consider a discrete-time nonlinear affine MAS withNidentical agents indexed by 1,2,...,N, interacting via a co mmunication network described by a topology G.Fort∈N andi=1,2,...,N, the dynamics of each agent is described by

Assumption 1: The graph G is undirected and connected.

Assumption2:Thereexist knownbasis functions F ∈Rnfand G ∈Rng×mthatspan f andg, respectively.

Assumption 2 means the use of a function library to describe the dynamics of the MAS, which is commonly valid in practical scenarios like mechanical and electrical systems, where the dynamics can be derived from first principles, but the exact systems parameters are unknown.Under Assumption 2, (1) can be represented as

where Λ ∈Rn×nf, Θ ∈Rn×ngare unknown coefficients of f, g with the corresponding sizenf,ngof basis functions.

We commence by defining the combined measurement variable,including the relative state information between neighbouring agents and the absolute states of a portion of agents as follows:

wheret∈N,ai jdenotes thei jth entry of the adjacency matrix A,anddiare constant scalars satisfyingdi＞0 fori=1,2,...,qanddi=0 fori=q+1,2,...,Nwithq={1,2,...,q}.

Then, the following distributed state-feedback consensus control law is adopted for the nonlinear MAS (1):

whereKi(t)∈Rm×nis the feedback gain matrix of agentito be designed at each time step.To this end, the closed-loop network dynamics resulting from (4) for (2) can be described as

Our goal is to design a state-feedback consensus control protocol(4) to stabilize the unknown nonlinear closed-loop system (5) subject to unknown external disturbancewi(t).Actually, the asymptotic stabilityishardtoachieve undertheinfluence ofdisturbances.Inline ofthis,define theconsensuserroraswith total numbers of agenti’s neighborsN¯i.A natural idea is to study the robustness of consensus protocols to external disturbances,which is formulated as an issue of additional UUB performance specification.However, the lack of knowledge about dynamics coefficients Λ , Θ challenges the controller design and its associated stability analysis.To tackle this, we introduce an advanced data acquisition mechanism.We begin by supposing that the controller side of each agentipossesses a buffer of sizeT∈N+.At eacht∈N, the buffer records the latestTinput-state samples of agenti, which are collected in data matricesXi,t+,Xi,t-, andUi,t-, given as follows:

Observe that whent∈[0,T-1], the indices of the samples in (6) are negative, indicating that the initial data is acquired through an offline experiment, as shown below, i.e., replacingtin (6) withT

In this way, a state-dependent model is constructed that captures each agent’s dynamics at each time stept, which we subsequently stabilize by treating it as a linear time-invariant (LTI) system.Building on this result, the ultimate aim is to design a distributed datadriven robust consensus controller for each agent at each time step directly from data that can effectively address Problem 1 for all linear-like systems in the set Σi.

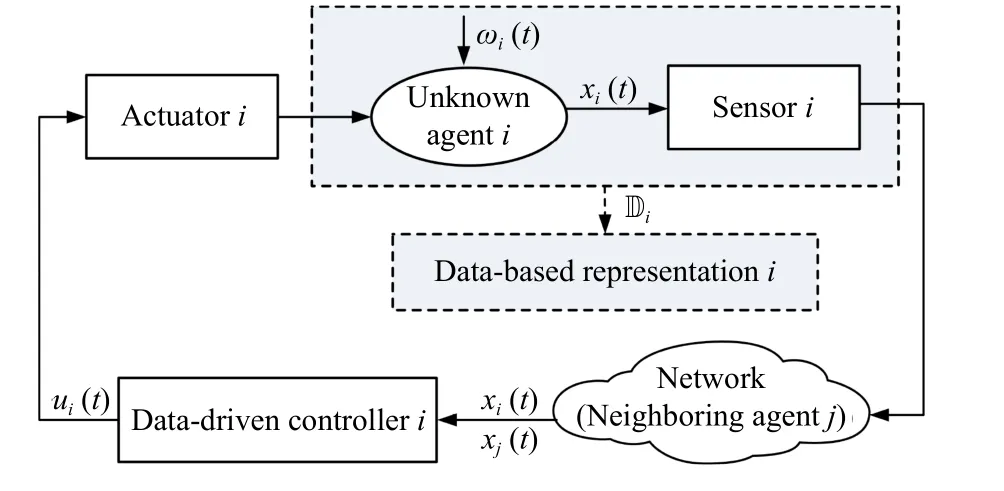
Fig.1.Distributed data-driven state-feedback consensus control.

Now, we are ready to discuss the properties associated to an equivalent data-based version of (10).An online distributed data-driven robust control algorithm for the unknown nonlinear MAS (1) under the control protocol (4), is presented in Algorithm 1, with stability guarantees provided below.

Theorem 1: Consider the nonlinear MAS (1) under the graph G.Suppose Assumptions 1-3 hold.For all [Λ,Θ]∈Σiandi∈{1,2,...,N}, if there exist matricesPi(t)=Pi(t)T≻0,Hi(t), andLi(t), and scalars τ ≥0, η ＞0 such that the following LMIs:

hold, then the UUB is achieved for any initial states under the statefeedback consensus control protocol (4).Moreover, the feedback gain matrix is computed asKi(t):=Li(t)Pi(t)-1/λ¯.

Algorithm 1 Online distributed data-driven robust control 1: Input: desired lifespan of the MAS ; data size T; data-generating input ; initial states ; matrices of the disturbance model , , and ; parameters , ; decide basis functions , ; performance matrices Q, R; and initial value of the Lyapunov function.Di Xi,T+ Xi,T- Ui,TT ui(0)∈Rm xi(0)∈Rn QdSd Rd τ η FG Vi(0)2: Collect initial T-long stream of state-input data and construc data matrices , , and.t ＜T 3: while do i=1,2,...,N 4: for do 5: Update data matrices , ,6: Solve the data-based optimization problem (11).Ki Xi,t+ Xi,t- Ui,t-7: Design controller gain matrix via Theorem 1.xi(t) j ∈Ni 8: Broadcast to agent.zi(t) xj(t)9: Compute from (5) based on the updated state.10: Update the control protocol (4) and the dynamics (5).11: end for 12: end while t

Fig.2.State trajectories of all agents under different approaches.

Conclusions: The consensus control problem of unknown nonlinear MASs has been addressed in this letter.An online distributed data-driven robust control approach was proposed to design controllers directly from disturbed data, along with rigorous stability guarantees.The resulting computational complexity at each step is comparable to that of designing a controller for a linear MAS of the same dimensions.Numerical examples have been provided under data-driven and model-based approaches, which showcases the effectiveness of the proposed method in terms of control performance and robustness dealing with disturbed data.Generalizing the results to the general directed topology constitutes interesting directions for future study.

Acknowledgments: The work was partially supported by the National Key R&D Program of China (2022ZD0119302) and the National Natural Science Foundation of China (U23B2059,61925303, 62173034, 62088101).