Fixed-Time Sliding Mode Control With Varying Exponent Coefficient for Modular Reconfigurable Flight Arrays

Jianquan Yang , Chunxi Yang ,,, Xiufeng Zhang , and Jing Na ,,

Abstract—The modular system can change its physical structure by self-assembly and self-disassembly between modules to dynamically adapt to task and environmental requirements.Recognizing the adaptive capability of modular systems, we introduce a modular reconfigurable flight array (MRFA) to pursue a multifunction aircraft fitting for diverse tasks and requirements,and investigate the attitude control and the control allocation problem by using the modular reconfigurable flight array as a platform.First, considering the variable and irregular topological configuration of the modular array, a center-of-mass-independent flight array dynamics model is proposed to allow control allocation under over-actuated situations.Secondly, in order to meet the stable, fast and accurate attitude tracking performance of the MRFA, a fixed-time convergent sliding mode controller with state-dependent variable exponent coefficients is proposed to ensure fast convergence rate both away from and near the system equilibrium point without encountering the singularity.It is shown that the controller also has fixed-time convergent characteristics even in the presence of external disturbances.Finally,simulation results are provided to demonstrate the effectiveness of the proposed modeling and control strategies.

I.INTRODUCTION

WITH the increasing demand for rotorcraft unmanned aerial vehicles (UAVs) in engineering applications,such as electrical power inspection and material transportation, the research of rotorcraft has attracted great attention.In recent years, the UAVs has developed additional capabilities to perform increasingly complex and sophisticated tasks.Examples include multimodal motion vehicles [1], [2], UAV swarms [3]-[6], modular or reconfigurable aircraft [7]-[13]and heterogeneous UAVs [14].Among those different UAVs,recently developed modular reconfigurable flight array(MRFA) system has certain advantages.In contrast to multiagent systems (MAS) and UAV swarms, MRFA can increase its capabilities by establishing physical connections.Another important capability of MRFA is to change its shape depending on the different tasks and environments.Therefore, modular reconfigurable flight array has great potential application in the military field and engineering practice.

To ensure efficient operation and perform complex missions of MRFA, dynamical modeling and control design is the foundation, which is also critical to enable its high-performance flight.Unlike conventional rotorcraft, the topological configurational variability of the MRFA necessitates that its dynamics model also has rapid variability.In [7], [12], [15], it is assumed that the center of mass of the aircraft is the origin of the airframe coordinate system when modeling the dynamics of MRFA.However, the arbitrary and variable topological configuration of the MRFA makes it difficult to obtain the center-of-mass information.When the physical structure of the flight array is altered, the modeling method based on the center-of-mass information can not realize the fast switching of the dynamics model.Therefore, a center-of-mass-independent modeling approach will be studied in this work, which enables fast online modeling of dynamics of MRFA under different operation regimes.

From the attitude control of modular aircraft, the existing work has made some important contributions.In [15], a robust feedback control strategy was used for a modular ducted-fan aircraft, and the controller is shown to possess a certain degree of robustness concerning the parasitic coupling between the controlled rotational and translational dynamics.For a fast and efficient attitude control problem of a modular aerial vehicle,an attitude compensation controller [16] was proposed to reduce the tracking and immunity errors of the nominal control loop by a quadratic programming approach to solve for the optimal auxiliary inputs.In [17], an adaptive attitude controller was designed for the control problem of an articulated modular vehicle, and the control gain was optimized to ensure the stable flight of the vehicle.In order to improve the controllability of the yaw rotation motion of a modular aircraft, an attitude controller [18] with a linear quadratic integral optimal control method was designed.However, the MRFA is a complex multiple-input multiple-output system, whose dynamics model has strong nonlinearities and uncertainties, which can have an impact on the stability and attitude control accuracy of the flight array system.Therefore, the controller design of MRFA should not only focus on robustness but also ensure fast convergence, which further presents challenges for the control design.

Sliding mode control (SMC) is a classical nonlinear control method that is robust to uncertainties and external disturbances [19].Therefore, SMC has been widely used in aircraft attitude control [20], [21], robot manipulator control [22],[23], autonomous underwater vehicle control [24], [25].Finite-time sliding mode control was proposed, which can make the state trajectory of the closed-loop system converge to the sliding mode surface, ensuring that the dynamic system reaches the equilibrium point in a finite time.The finite-time stability of SMC control strategy was also tailored for unmanned systems in [26], [27].However, the time upper bound derived from the finite-time stability theory is related to the initial values.To address this issue, a stability theory with a fixed-time was proposed in [28], [29] based on the Lyapunov method, which was applied to the design of a terminal sliding mode controller.In contrast to finite-time stability,fixed-time stability allows a convergence time upper bound to reach the equilibrium point, which is independent of the initial states.In particular, various fixed-time stabilization analysis and control designs were also developed in [30]-[33].Furthermore, fixed-time sliding-mode control methods have been studied for UAVs [34]-[37] for attitude control and formation control.However, to the best of the author’s knowledge,fixed-time sliding mode control has not been utilized with modular reconfigurable aircraft.

Motivated by the above mentioned discussions, this paper proposes a sophisticated modeling method and a fixed-time stable sliding mode control (FTSMC) method for MRFA’s height and attitude control.Firstly, the dynamic model of the MRFA is improved, where an advanced modeling method that does not consider the center-of-mass is proposed to allow the efficient control allocations for different topologies.Secondly,the detailed control design procedure of the FTSMC and stability proof of the MRFA height and attitude closed-loop control system are elaborated.The suppression of high-frequency chattering is also discussed.Comparative simulations are also given to verify the validity of the proposed schemes.

The main contributions of this work are listed as follows:

1) A control-oriented model containing the mass of the MRFA module is designed, which avoids the requirement of the center of mass of the MRFA and reduces the difficulty of handling the control allocation and over actuation.

2) The proposed FTSMC control suggests a novel reaching law with a variable exponent coefficient function depending on the system state, which retains the fixed-time convergence property but achieves a fast convergence speed over the classical fixed-time stability results [29], [38].

3) The proposed algorithms are verified based on a recently emerging MRFA plant, which also requests a constructive control allocation scheme to ensure its variety and adaptivity.

This paper is organized as follows: Section II describes the dynamics of an MRFA and formulates the control allocation problem.In Section III, a fixed-time sliding mode control is proposed based on the MRFA model.Comparative simulations on the MRFA model are used in Section IV to demonstrate the effectiveness of the proposed strategies.Finally,conclusions are given in Section V.

II.MODELING OF MRFA AND PROBLEM DESCRIPTION

A. Module Design

In this section, we design an MRFA based on module splicing.Through the arbitrary switching of flight modules, this MRFA can realize the change in the topological configuration,which extends the function of traditional aircraft.Each flight module consists of a hexagonal frame, brushless direct current motor, propeller, and electronic governor (Fig.1).In the studied MRFA, the modules are connected to each other by a connection mechanism.The hexagonal frame is made of carbon fiber material with a 200 mm side length and 6 mm thickness.The brushless motor is fixed in the geometric center of the hexagonal frame and the total mass of a single flight module is 235 g.

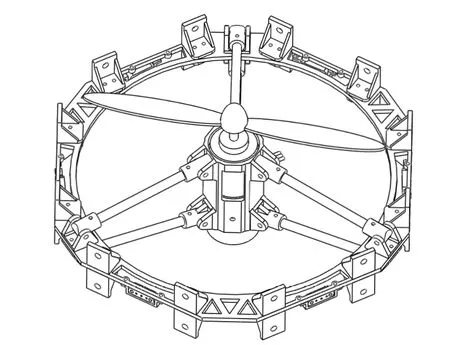
Fig.1.Flight module for modular reconfigurable flight arrays.

In order to facilitate the dynamic modeling and control design, we assume that all flight modules are homogeneous,including shape, mass, inertia, and actuators.The thrust and torque can be provided by the flight module.The thrust is expressed as Fi=Kf ui(i=1,2,...,n,n≥4), whereuidenotes the pulse width modulation (PWM) input of thei-th rotor.Similarly, Mi=Kτuidenotes the counter-torsional torque generated by thei-th propeller rotation.The relevant parameters and their annotations are listed in Table I.

The MRFA formed by splicingnmodules is defined as MRFA-n(Fig.2).These modules are connected by a lateral connection mechanism to form a planar MRFA-n, which is considered as a rigid body.Compared to traditional multirotor vehicles, the MRFA enables the number of modules and the configuration of the aircraft to be adjusted according to actual engineering requirements to accomplish more complex and variable missions.

B. Coordinate Systems

Accurate representation of the position and attitude informa-tion of the MRFA in space is a prerequisite for the control design for the MRFA, and the three coordinate systems shown in Fig.2 are defined as follows:

TABLE I THE RELATED PARAMETERS AND THE CORRESPONDING INTERPRETATIONS

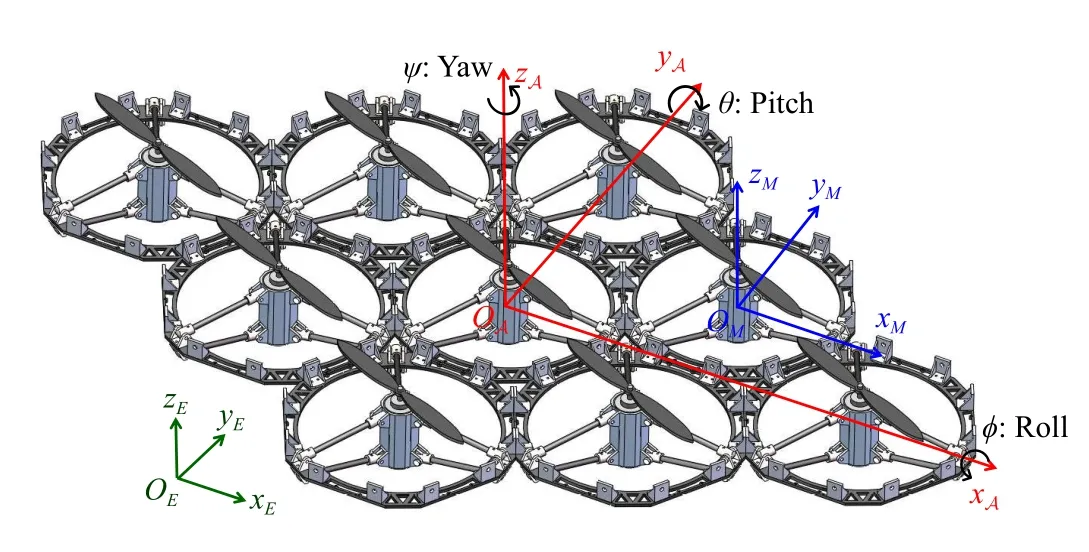
Fig.2.Coordinate schematic of MRFA (The earth coordinate frames, module coordinate frames, and flight array coordinate frames are represented by the green, red, and blue axes, respectively).

1)Earth Coordinate Frame(OE(xE,yE,zE)): The three axes of the Earth coordinate frame satisfy the right-hand rule and thez-axis is specified to be oriented upwards.In addition, the position of the MRFA in the earth coordinate system is defined asXE=[xe,ye,ze]T, and the attitude angles of MRFA are represented by the Euler angles Θ=[φ,θ,ψ]T, where,φ,θ,ψdenote the roll, pitch and yaw, respectively.

2)Module Coordinate Frame(OM(xM,yM,zM)): The module coordinate frame is a right-handed coordinate frame, and the coordinate origin is located at the center of the module.Itsz-axis direction is the same as the thrust direction of the propeller on the module.To simplify the model, we assume that all module coordinate frames are on the same plane and point in the same direction.

3)Flight Array Coordinate Frame(OA(xA,yA,zA)): We choose an intermediate module in the MRFA (which may not be the center of mass of the MRFA) as the origin of the MRFA coordinate system, and the orientation of a coordinate system is the same as the orientation of the module coordinate system.In this way, each module’s location informationXA=[xAi,yAi,zAi], the MAFA translational speedVA=[u,v,w]Tand rotational velocity ωA=[p,q,r]Tare defined in the MRFA coordinate frame.

According to the above coordinate system, the inertia tensor of the MRFA will be calculated.Since the MRFA coordinate system and the module coordinate system have the same orientation, we can compute the MRFA inertia matrix,denoted byJA, based on the inertia matrix of a single moduleJ=diag(Jxx,Jyy,Jzz)by using the parallel axis theorem [39].

which can be simplified as

Its inverse matrix is given by

C. Dynamic Model of MRFA

Based on the above definition of coordinate systems, the dynamics of MRFA can be modeled by the Newton-Euler method [40], where the translational movement is described as

where sφ=sin(φ) and cφ=cos(φ).Other attitude angles can be represented by similar rules.Tzis the thrust relative to the earth coordinate system in the same direction as thezE-axis.

In the presence of torque input, the rotational motion of the MRFA can be given as

where [τx,τy,τz]Tis the moment vector of rotation around thexA,yA,zAaxes.

D. Control Relation Equation

The thrust and torque required for the flight motion of the MRFA are provided by each flight module, and the analysis of forces and moments is the prerequisite to ensuring the stability of the MRFA.In this subsection, the force and torque analysis of the MRFA is carried out, and then the control relationship equation is constructed to realize the stable control of MRFA.

In the defined MRFA coordinate frameOA(xA,yA,zA), we specify: κ∗=2 if the propeller is rotating clockwise; otherwise, κ ∗=1.

When the topological configuration of MRFA changes, its dynamic model also changes, which poses challenges to airborne self-assembly and self-separation control of MRFA.To address this issue, the inertia parallel axis theorem (1) and the control relation (6) are used to reflect the difference between different topological configurations, so that the dynamic model of the MRFA can be updated online.

Fig.3 shows three modular reconfigurable flight arrays with different topological configurations.The difference in the topological configurations is reflected by the coordinate information of the flight module, as shown in Table II.Since the dynamic model does not depend on the centroid information,the calculation of the centroid is avoided, and the modeling steps are simplified.When the topology changes, the corresponding dynamic model can be quickly established through the geometric relationship between the modules.

Remark 1: In order to balance the air reverse torque caused by the propeller rotation, the propeller is generally set as a clockwise rotating propeller (thrust generated by clockwise rotation) and a counterclockwise rotating propeller (thrust generated by counterclockwise rotation).For example, in the MRFA shown in Figs.3(a) and 3(c), the propellers in modules #1, #3, and #5 are set to rotate counterclockwise, and #2,#4, and #6 are rotated clockwise.

Remark 2: By means of the thrust calculation Fi=Kf ui, the reverse torqueMi=Kτuiand(6),weestablishthe pulsewidth modulation (PWM)inputuiandthetorque[TZ,τx,τy,τz]T,which are indicated in the control relationship equation (6).In addition, the influence of the flight module’s gravity is also considered, which allows the control relationship (6) to still hold when the MRFA topological configuration changes or the actuators have faults.

Remark 3: Compared with the center-of-mass-based modeling methods proposed in [12], [15], [41], it is difficult to obtain the center-of-mass information rapidly and accurately for the MRFA.In addition, when the number of modules and the MRFA topological configuration change, the center-ofmass also changes, which makes the center-of-mass calculation complicated.In this paper, a modeling method independent of the center of mass is proposed, which can realize the fast online updating of the MRFA dynamic model.

Fig.3.Different flight arrays with six modules MRFA-1, MRFA-2 and MRFA-3.Red represent clockwise rotation, blue is counterclockwise rotation.

TABLE II DIFFERENCES IN MRFA WITH DIFFERENT TOPOLOGICAL CONFIGURATIONS

E. Control Allocation

To describe the control relationship equations of the MRFA more clearly, (6) is rewritten in the following form:

whereP=diag(Kf,Kf,Kf,Kτ) is the coefficient matrix of propeller.According to (7), we can get the control efficiency matrixBe1∈R4×nand the gravity compensation matrixBe2∈R4×nas

According to (7), the virtual control input is given by

where τ=[Tz,τx,τy,τz]T∈R4is the virtual control input andu=[u1,u2,...,un]T∈Rnis the PWM input (the real control input).G=[m1g,m2g,...,mng]T∈Rnis the gravity vector.

From (7) and (8), we know that the MRFA system is overactuated (4 ＜n), i.e., the number of actuators is greater than the number of virtual control inputs.This implies that the control effectiveness matrixBe1has a nontrivial zero space.Hence, there is an infinite number of control effortsusatisfying (10) for a given virtual control inputτ.

In order to obtain the desired control effortu, a control allocation strategy based on the energy optimization is proposed as

In [42], a matrix pseudo-inverse method is proposed to solve the above optimization function, and the actuator control input is obtained

With the control allocation (12), virtual control inputs are allocated to each actuator with the minimal energy consumption, thus enabling motion control of systems with actuator redundancy such as MRFA.

Remark 4: In contrast to the control allocation methods given in [7], [43], [44], the gravity termGis introduced into the control allocation, and it is compensated by the gravity compensation termBe2.Therefore, the center-of-mass information is no longer necessary in the modeling process.In addition, the proposed control allocation method can still achieve stable flight when an actuator failure occurs.

III.ROBUST FIXED-TIME SLIDING MODE CONTROLLER DESIGN

In this section, we design a fixed-time robust control to achieve height and attitude tracking control of MRFA with different topological configurations.The control system is shown in Fig.4.

Fig.4.The closed loop control block diagram of MRFA system.

A. Preliminaries

For a nonlinear system

wherex(0)=x0is the stable equilibrium point, andf(·) is a nonlinear continuous function withf(0)=0.

Definition 1[45],[46]: If system (13) satisfies: there exists a positive definite functionTs(x0):R →R+withTs(x(0))=0,whent→Ts(x0),x(t)→0 , and ∀t∈[Ts(x0),+∞],x(t)=0,then system (13) is globally finite-time stable with the settling-timeTs(x0).

Definition 2[28]: System (13) is globally fixed-time stable if: 1) It is globally finite-time stable; 2) The settling-timeTs(x0) has an upper boundTmax.

Lemma 1[28],[32],[47]: The system (13) is practically fixed-time stable, if there is a positive functionV(x)∈R satisfying

wherea＞0,b＞0, α ＞1, 0 ＜β ＜1, and ρ ∈R are positive constants, then the statexconverges into a residual setS0within the fixed-timeTmaxgiven by

The residual set S is defined as

with the constant 0 ＜Δ ＜1.Specifically, the statexconverges to the origin for ρ =0.

Lemma 2: Consider a positive definite functionV(x):R →R+for system (13) fulfilling

wherea＞0,b＞0,c＞0, 0 ＜β ＜1, α ＞1, and ρ ∈R are positive constants.Then system (13) is globally fixed-time stable,and the statexconverges into the residual set S within a fixed-timeTmaxgiven by

The residual set S is defined as

with the constant 0 ＜Δ ＜1.Specifically, the statexconverges totheoriginfor ρ=0.

Proof: The detailedproof will be given in the Appendix.■

Remark 5: When we setc=0, (17) is simplified to (14), and thus Lemma 1 can be considered as a specific case of Lemma 2.However, comparing (18) with (15), it is clear that the settling time can be tuned small by using a largec＞0, so as to enhance the convergence rate.Moreover, the ultimate residual set S of Lemma 2 in the presence of disturbance ρ can also be made smaller than that of Lemma 1 by setting a largec＞0 based on (16) and (19).

Lemma 3[48]: The following inequality holds for any constants ε ＞0 and η ∈R:

δ=e-(δ+1)δ=0.2785

whereδis a constant satisfying , e.g.,.

B. Fixed-Time Reaching Law

Some existing reaching laws used for fixed-time sliding mode control schemes use constant coefficients [38], [49].A fixed-time sliding mode control approach was proposed by using variable exponent coefficients in [29], where the fixedtime stability is obtained based on Lemma 1.In order to obtain faster convergence rate and retain robustness, a new robust fixed-time reaching law is proposed and the convergence is analyzed by using Lemma 2.that the disturbancefulfills|d(t)|≤d¯ forallt≥0.The sliding

Theorem1: Assumethatthere exists apositivescalard¯ such mode control reaching law is

Proof: Consider a Lyapunov function as follows:

Then, we have

When one sets largek3such thatk3-d¯ ＞0 and(p+1)/2 ＞1 hold, Lemma 2 ensures that the system statexreaches the origin in a fixed-time given in (22).Moreover, the sign function t urbancesd(t)and retains therobustness.x→k3sgn(x)withk3＞d¯ allowsthe rejection of bounded dis-

We compare the convergence response of reaching law (21)with disturbanced(t)=sin(10t) under different initial conditionsx(0)=8, 10, -5, -14, 16, 20 via numerical simulations,wheretheparametersaresetask1=2,k2=6,k3=2,p=1.2,λ=0.2,µ=0.1andd¯=1.As shown inFig.5,theproposed reaching law can obtain fixed-time convergence ofxto zero withTmax=1.489 s even in the presence of disturbanced(t).

Fig.5.Convergence curves for different initial conditions.

C. Robust Fixed-Time Control of MRFA

Since the altitude changes of the aircraft are directly related tothe dynamical behavior of the actuators, here we investigate the height and attitude control of the MRFA.The control state vectorx(t) is defined

Now, we derive the control inputs based on the equivalent control input method.Hence, the following control law for the heightzecan be designed:

where τ10is the control action to compensate for nonlinear dynamics in (29), and τ11is the reaching control used to deal with external disturbances and unmodeled dynamicshz(t),which are given by

Similarly, the pitch, roll and yaw controllers are given by

where

and

In the above control laws, τi0is used to compensate for the nonlinear dynamics associated with the system, i.e., the rotational inertia (1) and the control relationship (6), and τi1is the reaching control input to resist external perturbations and achieve reaching phase dominated by Theorem 1.Therefore,the proposed controller can easily be applied to MRFA with different topological configurations by incorporating the developed control allocation.Moreover, it is clear that the above designed sliding mode variablessiare free of singularity issue.

D. Stability and Convergence Analysis

The stability of the control system, the convergence of the sliding mode surface and the tracking error are analyzed.For brevity, we take the flight altitude control τ1of the MRFA as an example.The analysis and conclusions for the other controllers τ2, τ3and τ4are similar to the following theorem.

Theorem 2: The controller (30) obtained with the sliding mode surface (28) and the reaching law (21) ensures that the control errorx1converges to a small residual set in a fixedtime

whereT1is the convergence time of sliding mode variables1specified by Theorem 1, andT2is the convergence time of control errorx1on the sliding mode surfaces1=0 specified by Lemma 1.

Proof: First, the convergence analysis of the sliding mode variables1is derived by substituting (30) into (29) as

According to Theorem 1, system (35) reaches the sliding manifolds1(t)=0,t≤T1for any initial states(0)=s0within a fixed-time

Now, the convergence analysis of tracking errorx˜1will be proved.As proved, the reaching law (35) makes the sliding mode variables1converge to zero in a fixed-time, i.e.,s1(t)=0 fort≤T1.Thus, one has from (26) and (28) that

Consider the Lyapunov function defined as

Taking the derivative ofV(x˜1) along (37), we have

According to Lemma 1, the tracking errorx˜1converges from the initial conditionx˜1(0)=x˜10to a small set around zero in a fixed-time

E. Chattering Suppression

For suppressing the chattering in the control τi1caused by the actionki3sgn(si), we can further use a hyperbolic tangent function to replace the sign function, while for the chattering stemming fromki1q(si)ri(si)sgn(si), a variable gainN1(s1) is designed to reduce the chattering.Therefore, the control law(32) was redesigned to

whereN1(s1)=l1+(o1-l1)e(-z1|s1|z1).l1＞1,o1＜1 andz1＞0 are real numbers.

For the varying gainN1(s1), it can be found thatN1(s1)tends to bel1if |s1| i s large, otherwiseN1(s1) approaches too1for small |s1|, i.e.,o1≤N1(s1)＜l1.Therefore, the sliding mode variable has a faster convergence rate whens1is far away froms1=0 , and the variable gainN1(s1) has also a suppression effect on the high frequency chattering wheno1satisfies 0 ＜o1＜1 and thuss1tends towardss1=0.

Substituting (31) and (41) into (29), the sliding mode variable is govern by

To analyze the convergence of (42), we consider the following Lyapunov function:

Taking the time derivative of (43) along with (42), and using Theorem 1, we have

In conclusion, combining (44) with (45) yields

By using Lemma 2, the sliding mode variables1converges to a small set around zero in a fixed-time under the control law (41).In addition, the use of variable gainN1(s1) and hyperbolic tangent function tanh(s1/ε1) enables the designed control to have strong robustness and good suppression of high frequency chattering in the control actions.

The above modifications can also be applied to τ21, τ31and τ41, and the same conclusions can be obtained accordingly.

F. Control Parameter Selection

IV.SIMULATION VALIDATION

In this section, numerical simulations are performed to test the effectiveness of the proposed control algorithms (30), (33)and control allocation (12) in terms of trajectory tracking performance and robustness behavior against bounded uncertainties and disturbances.

1) In order to illustrate the effectiveness of the controller(30), the dynamic model of MRFA- A1is first used.To test the chattering suppression and enhance the tracking performance,the proposed control strategy is compared with the sliding mode control strategy given in [29].

We perform attitude tracking control based on the MRFAA1.First, the Band-Limited White Noise with noise power 0.05 and sampling time is 0.1 is used as the disturbance injected into the system, and the initial states are[ze0,φ0,θ0,ψ0]=[0,0,0,π/3].The control parameters are given in Table III and simulation results are shown in Fig.6.To illustrate the controller performance, the accumulation tracking errors are given in Table IV.The accumulative error is calculated as

wherekis the sampling point used in the simulations.

TABLE III CONTROLLER PARAMETERS

Fig.6.Closed-loop response of MRFA- A1 9.5 for height and attitude angle.

TABLE IV ACCUMULATED TRACKING ERRORS

It can be seen from Fig.6 and Table IV that control (30) can achieve good tracking performance for height, roll, pitch, and yaw dynamics.Moreover, compared with the controller in[29], the proposed control (30) has a faster convergence speed and higher convergence accuracy.The corresponding curves of virtual control inputs of these two different controllers are given in Figs.7 and 8, from which we can validate that the control actions are smoother than those of [29], i.e., the control has a significant suppression effect on chattering.To demonstrate the effectiveness of the control allocation (12),we perform real-time control inputsu1,u2,u3,u4,u5,u6of MRFA-1 in the hovering state (zd=5, φd=0, θd=0,ψd=0).Fig.9 shows simulation results of the control allocation.It can be seen that in the climbing stage of the MRFA, the outputs of motor #3 and #4 are larger, since the lift is mainly provided by#3 and #4, while the outputs of motor #1, #2 and #5, #6 show the symmetry of the origin of the flight array coordinate frame, which ensures the stability of the MRFA attitude.Fig.10 shows the relationship between the thrust required by hovering and the thrust provided by the motor.The sum of thrust generated by each actuator is the same as the thrust required by the MRFA to complete the hovering task.This illustrates the effectiveness of the control allocation (12), where the virtual control inputs can be allocated to each motor with the energy-optimal policy.

Fig.7.Virtual control input Tz, τx, τy and τz of FTSMC.

2) To illustrate the generality of the proposed control for different MRFA models, we apply it to different topological configurations of MRFA (as shown in Fig.3 for MRFA-2 and MRFA-3).

We select the control parameters as given in Table V.The perturbation [h2z(t),h2φ(t),h2θ(t),h2ψ(t)]Tof MRFA-2 are defined ash2z(t)=h2φ(t)=h2θ(t)=h2ψ(t)=0.5sin(2πt)+W,where W is the band-limited white noise (power is 0.05 and sampling time is 0.1).Similarly, the perturbations[h3z(t),h3φ(t),h3θ(t),h3ψ(t)]Tof MRFA-3 are defined ash3z(t)=h3φ(t)=h3θ(t)=h3ψ(t)=0.5sin(πt)+sin(2πt)+W.The control results are shown in Figs.11 and 12.Fig.11 shows the trajectory tracking performance of the designed controller for different MRFAs.The tracking error curves of MRFA-2 and MRFA-3 for the same reference are given in Fig.12.It is clear that the control proposed in this paper can be applied to MRFA with different topological configurations,which illustrates its flexibility due to the control allocation and the robustness against disturbances.Specifically, even though there are different unmodeled dynamics and external perturbations, the control can still obtain a relatively similar control result.

Fig.8.Virtual control input Tz, τx, τy and τz of [29].

In summary, the control algorithms presented in this paper can achieve satisfactory control results, have good robustness,and suppress the chattering effectively.Moreover, the designed fixed-time convergent sliding mode variable can maintain a fast convergence speed in the whole process, which ensures that the controlled system can track the reference state in a fixed-time.

V.CONCLUSION

In this paper, a center-of-mass-independent modeling method of novel MRFAs with a variable topological configuration is suggested to facilitate the control design.Moreover, a fixed-time sliding mode control method is proposed to achieve flight control of MRFA.Considering the arbitrary configuration of the MRFA and the difficulty of obtaining the center-ofmass information, the modeling method does not need to remedy the use of the center-of-mass position, and a control relationship equation with center-of-gravity compensation is designed to obtain the control allocation.To retain the overall fixed-time convergence of tracking errors, a fixed-time convergent sliding mode surface with variable exponent coefficients is designed.To address the high-frequency chattering encountered in the sliding mode control, varying gain and hyperbolic tangent functions are used in the controller, while the robustness against the unmodeled dynamics and external disturbances can be retained.Numerical simulations are given to verify the effectiveness and generality of the proposed control schemes for MRFA with different topologies and parameters.Future work may consider the fault detection and tolerant control of modular reconfigurable flight arrays to retain its survivability under actuator faults.

Fig.9.Control input of MRFA- A1 in hovering state.

APPENDIX

Proof: Inequality (17) can be rewritten as

Integrating both sides of the inequality gives

Fig.10.MRFA- A1 lift combined force curve.

TABLE V CONTROLLER PARAMETERS OF MRFA- A2 AND MRFA-A3

Fig.11.Height, attitude tracking curves of MRFA- A2 and MRFA- A3.

Fig.12.Height, attitude tracking error curves of MRFA- A2 and MRFAA3.

LetΛ˙(ϱ)=0, we get

and it follows that:

The upper bound on the minimum settling time is obtained by substituting (59) into (55)

Next, the solving process of residual set (19) will be given.To facilitate the calculation, (17) is considered in three cases.

Case 1: Inequality (17) can be rewritten as

From (61), when satisfyingV(x)≥ρ/((1-Δ)c), we getV˙(x)≤-aVα(x)-bVβ(x)-ΔcV(x), At this time, the system statex(t) will converge to the set

Case 2: Inequality (17) can be rewritten as

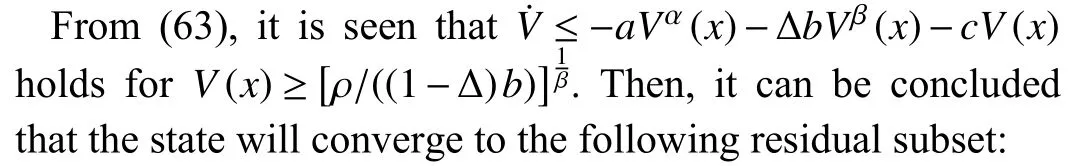
Case 3: Similarly, the following inequality is also considered:

Inthiscase,V˙(x)≤-ΔaVα(x)-bVβ(x)-cV(x)holds forV(x)≥[ρ/((1-Δ)a)]α1.Similarly,itisconcluded that thestate will converge to the following residual subset S13in a fixedtime.And the subset of residual is denoted as follows:

Based on the above analysis, when the system (13) satisfies(17), the system state will converge to the residual set