Even Search in a Promising Region for Constrained Multi-Objective Optimization
Fei Ming , Wenyin Gong ,,, and Yaochu Jin ,,
Abstract—In recent years, a large number of approaches to constrained multi-objective optimization problems (CMOPs) have been proposed, focusing on developing tweaked strategies and techniques for handling constraints.However, an overly finetuned strategy or technique might overfit some problem types,resulting in a lack of versatility.In this article, we propose a generic search strategy that performs an even search in a promising region.The promising region, determined by obtained feasible non-dominated solutions, possesses two general properties.First, the constrained Pareto front (CPF) is included in the promising region.Second, as the number of feasible solutions increases or the convergence performance (i.e., approximation to the CPF) of these solutions improves, the promising region shrinks.Then we develop a new strategy named even search,which utilizes the non-dominated solutions to accelerate convergence and escape from local optima, and the feasible solutions under a constraint relaxation condition to exploit and detect feasible regions.Finally, a diversity measure is adopted to make sure that the individuals in the population evenly cover the valuable areas in the promising region.Experimental results on 45 instances from four benchmark test suites and 14 real-world CMOPs have demonstrated that searching evenly in the promising region can achieve competitive performance and excellent versatility compared to 11 most state-of-the-art methods tailored for CMOPs.
I.INTRODUCTION
CONSTRAINED multi-objective optimization problems(CMOPs) refer to optimization problems with two or three objective functions and some constraint conditions,which widely exist in real-world applications and scientific research, such as vehicle scheduling of the urban bus line [1].
In recent years, many research efforts have been devoted to developing approaches for solving CMOPs [2].Researchers in the multi-objective optimization field have proposed many new constrained multi-objective optimization evolutionary algorithms (CMOEAs), most of which focused on algorithmic strategies or constraint-handling techniques (CHTs).Regarding the algorithmic strategies, ignoring or relaxing constraints in an auxiliary problem to help the algorithm solve the original CMOP [3], [4] and balancing the optimization of objectives and satisfaction of constraints [5], [6] are both popular.As for CHTs, theε-constrained technique [7], [8], the penalty function [1], and new CHTs [9] have been improved to handle CMOPs with more complex features by utilizing valuable infeasible solutions.However, as pointed out in the experiments of [10] and according to the No Free Lunch theory [11], a specific strategy or tailored technique, especially if it is labor-intensively designed and complicated, might overfit some problem types1Overfit in this work indicates that a method performs extremely well on some problems but unusable (i.e., cannot find a desirable number of applicable solutions) on others..As a consequence, these methods lack versatility and may be hard to use in real-world applications that are always subject to unknown features and difficulties.
To overcome the above shortcomings, this work proposes to conduct an even search in the promising region for CMOPs.To be more specific, the main contributions are as follows:
1) We propose an approach that makes use of the obtained feasible non-dominated solutions to define a promising region.The promising region has two properties.First, the constrained Pareto front (CPF) must be included in the region no matter what features the CMOP has.Thus, searching in the promising region helps search the CPF.Second, as either the number of feasible solutions or the convergence (i.e., the approximation degree to the CPF) improves, the promising region will shrink.Thus, the region where the even search should be performed becomes smaller and is more precisely defined.
2) We develop an even search method that utilizes valuable solutions located in the promising region to assist the search for the CPF.Specifically, those non-dominated solutions with good convergence and diversity are used to accelerate the approximation to the CPF and help the search algorithm escape from local optima.Moreover, those feasible solutions under a constraint-relaxed condition with good feasibility and diversity are used to exploit the detected and explore the undetected feasible regions.In addition, we use the minimum Euclidean distance between solutions as a measure to enhance diversity.In this way, the preserved solutions are well-distributed in valuable areas in the promising region to achieve an even search.Moreover, a simpleε-constrained method,containing only one parameter, is designed to evaluate the feasibility under a constraint-relaxed condition.
3) Based on the above methods, we propose a new CMOEA named constrained multi-objective optimization based on even search (CMOES).CMOES contains two stages, the first stage aims to find feasible non-dominated solutions and approximate the CPF, while the second stage conducts the even search in the determined promising region.
Compared to most existing methods in the constrained multi-objective optimization community, our methods have the following two features.First, since the CPF must be included in the promising region for any CMOP, the strategy to search in the promising region works for any class of CMOPs.Second, our proposed even search method contains only one parameter and does not require problem-specific fine-tuning.The proposed methods are tested on 45 instances from four benchmark suites with very different features and difficulties and 14 real-world CMOPs with unknown features and difficulties.Extensive experimental results have demonstrated that searching in the promising region can achieve competitive performance and excellent versatility compared to 11 most state-of-the-art CMOEAs.
The remainder of this article is organized as follows.Section II introduces the related work and backgrounds.Section III elaborates on the proposed CMaDPPs.Then, experiments and analysis are presented in Section IV.Finally, conclusions and future research directions are given in Section V.
II.LITERATURE REVIEW AND MOTIVATIONS
A. Preliminaries of CMOPs
Without loss of generality, a CMOP is formulated as follows:
wheremdenotes thenumberof objectivefunctions;x=(x1,...,xn)Tisann-dimensionaldecision vector;nisthe number of decision variables; x ∈S , and S ⊆Rnis the search space.gi(x) andhj(x) are thei-th inequality andj-th equality constraints, respectively.qdenotes the number of constraints.
For a CMOP, the degree of thej-th constraint violation(denoted ascvj(x)) of x is
whereσis a small enough positive value to relax the equality constraints into inequality ones.The overall constraint violation (CV) of x is calculated by
A solution x is feasible ifCV(x)=0; otherwise, it is infeasible.
B. Existing Approaches to CMOPs
Based on the basic ideas and foci, existing approaches for CMOPs could be roughly divided into three categories.
1)Using Auxiliary Evolution: The first category uses one or more auxiliary problems to assist the evolution of the original problem.Generally, this kind of method performs well on those CMOPs whose CPF is the same as, part of, or near the unconstrained Pareto front (UPF).Liu and Wang [3] proposed a two-phase algorithm that uses the first phase to solve a single-objective optimization problem transferred from the original CMOP to assist in solving the original problem in the second phase.Liet al.[4] proposed a two-archive algorithm that uses a convergence-oriented archive to store feasible solutions and pursue convergence and meanwhile uses a diversityoriented archive to store solutions with good diversity to assist in searching the objective space.Tianet al.[12] proposed a new coevolutionary framework that evolves a population for the unconstrained helper problem to assist the original problem, besides, the new framework performs independent mating to avoid generating useless offspring.Jiaoet al.[13] proposed a multi-tasking framework that conducts an auxiliary task to search for the CPF in feasible regions derived from the original problem through anε-constrained technique.
2)Balancing Convergence and Feasibility: The second category solves CMOPs by balancing the convergence (i.e.,approximation to the CPF) and the feasibility (i.e., satisfaction of constraints).Generally, this kind of method could perform well on CMOPs whose feasible regions are relatively large so the switches of preference between constraints and objectives need not be complicated.Tianet al.[5] proposed an auto-switched two-stage algorithm that uses one stage for the unconstrained helper problem and the other for the original problem and automatically switches between these two stages according to the state of the population.Lianget al.[6]proposed utilizing the relationship between the CPF and the UPF by learning the distribution of the CPF and UPF to balance convergence and feasibility.Yuet al.[14] proposed to dynamically adjust the selection preference between convergence and feasibility during the evolutionary process considering the state of the current population.Maet al.[15] proposed a new fitness evaluation function that automatically adjusts the weights of convergence and feasibility according to the current population state to balance the optimization of objectives and constraints.
3)Utilizing Infeasible Solutions by CHTs: The third category utilizes valuable infeasible solutions by improving or developing new CHTs to assist the search for the CPF.This kind of method could perform well in dealing with CMOPs with complex constraints and large infeasible regions.However, most CHTs were labor-intensively tailored, and thus,they might be overfitting to some benchmark problems but not applicable to others.Zhouet al.[16] proposed an infeasible solutions diversity maintenanceε-constrained handling method that utilizes infeasible solutions with good diversity to search in the objective space.Yuanet al.[9] proposed using valuable infeasible solutions determined by a comprehensive criterion that evaluates the potential value of each infeasible solution from different aspects.Fanet al.[7] proposed a pushpull search framework that pushes the population toward the UPF by ignoring constraints in the pushing stage and pulls it back to the CPF in the pull stage using anε-consrainted technique.Ma and Wang [1] proposed a shift-based penalty function that first shifts the positions of infeasible solutions according to the near feasible solutions, and then, the shifted infeasible solutions are penalized based on their constraint violations.Sunet al.[8] proposed a new constraint relaxation strategy by adopting different constraint relaxations in feasible sub-population, semi-feasible sub-population, and infeasible sub-population.
C. Motivations
As mentioned above, specific and complicated strategies and techniques might be suitable for some problem types but not applicable to other types, resulting in a lack of versatility2Evidence can be found in Secion IV, where we perform various experiments to test performances of different CMOEAs on different CMOPs.The results clearly reveal that some CMOEAs using a specific or complicated strategy (e.g., BiCo and MFOSPEA2) perform very well on one kind of CMOP but cannot handle other features of CMOPs..If we need to solve a real-world CMOP whose features and types are unknown, it is hard to determine which strategy or technique to use.Some strategies and techniques might even be too complicated to use.Therefore, in this paper, we investigated the properties of a promising region and the effectiveness of searching evenly in it for CMOPs, aiming to develop a simple but versatile approach that could suit CMOPs with different features and challenges.
Fig.1 illustrates the basic concepts of our proposed promising region definition.As shown in Fig.1(a), if we obtain a feasible solution, the non-dominated region, marked as the region within the dashed lines, is named the promising region.If we obtain more feasible solutions, the size of the promising region could be reduced.In the following, we prove that the CPF must be contained in the promising region.

Fig.1.Illustration of the proposed promising region concept.(a) Promising region determined by one feasible non-dominated solution; (b) Promising region determined by multiple feasible non-dominated solutions.
First, we introduce the basic definitions of constrained multi-objective optimization.
1)Pareto Dominance: For two solutions x1, x2∈S.x1is said to Pareto dominate x2(denoted as x1≺x2), if and only iffi(x1)≤fi(x2) for ∀i∈{1,...,m} andfi(x1)<fi(x2) for∃i∈{1,...,m};
2)Constrained Pareto Set(CPS): A set thatfor∀x⋆⊂CPS, ∄ x ∈S such that φ (x)=0&&x ≺x⋆;
3)Constrained Pareto Front(CPF):CPF={F(x)|x ∈CPS}.Then, given PR is the point set of the promising region determined by a solution x, and S is the point set distributed on the CPF.P R ∈S, S ∈S.
Suppose S ∉PR, i.e., not all CPF is in the promising region.
∵S ∉PR,
∴∃y ∈S, x ≺y,
∵∀x⋆⊂CPS∄x ∈SCV(x)=0&x ≺x⋆
, such that ,
∴∄x, x ≺y,
∴ they conflict with each other,
∴S ∈PR.
Therefore, if we can search evenly in the promising region,the CPF could be obtained no matter how the feasible regions distribute or what the relationship between CPF and UPF is.It is important to note that the term even search (search evenly)in this work means maintaining a set of well-spread solutions in the promising region that covers as many of its areas as possible.
Fig.2 provides an artificial scene where feasible regions are discontinuous and randomly distributed.The dot represents the old feasible solution and the star represents the new feasible non-dominated solutions.In Fig.2(a), the old solution will be deleted because it is dominated by the new feasible solution.In Fig.2(b), two more feasible solutions can be used to determine the promising regions because they are all feasible and non-dominated by each other.As shown in Fig.2, when the evolution processes, more feasible solutions can be obtained (i.e., the situation of Fig.2(a)) and the convergence of these solutions can be improved (i.e., the situation of Fig 2(b)).Then, the promising region shrinks so searching evenly in it becomes easier as the evolution proceeds.

Fig.2.Illustration of the variations of the promising region during the evolutionary process.(a) Variation of promising region when the convergence of feasible non-dominated solution improves; (b) Variation of promising region when the number of feasible non-dominated solutions increases.
Based on the above considerations, we proposed a new method that conducts an even search in the promising region for handling CMOPs, which will be detailed in the next section.
III.PROPOSED METHODS
A. Determine Solutions in Promising Region
In this part, we first present the method to determine whether a solution is in the promising region.As illustrated and proved in Section II-C, if a solution is not dominated by the obtained feasible solutions, it is in the promising region.Therefore, we use the method presented in Algorithm 1 to achieve this.In our method, a vector PR is initialized by ones with size S (Line 1).Then, for every solution in S, if any solution of the obtained feasible solution set F dominates the solution in S (Line 4), its mark in PR is set to zero (Line 5).Therefore, those solutions in S marked ones are in the promising region.On the contrary, solutions marked zero are not in the promising region.Since the input of this procedure contains the obtained feasible solution set F , and F is updated every generation which will be introduced in Section III-D,the shrink of the promising region can be achieved.

Algorithm 1 Identification of Solutions in PR Require: (solution set), (obtained feasible non-dominated solution set)PR S F Output: (the mark whether in PR)PR ←1: Initialize the marks as ones;F 2: for each solution x in do S 3: for each solution y in do x ≺y 4: if then PRx ←0 5: ;6: end if 7: end for 8: end for A 9: return
B. Even Search
In this part, we introduce the proposed even search strategy which is presented in Algorithm 2.This method aims to preserve valuable solutions well-spread in the promising region,achieving an even distribution to assist the search for the CPF.First, all solutions in the promising region are preselected to a temporary solution set S (Lines 1 and 2).Then, the first proportion of the population for the next generation P1is selected(Lines 3-9).The first proportion contains non-dominated solutions with a good degree of diversity.The diversity is guaranteed by deleting redundant solutions with smaller closest distances.The closest distance of any solution x is calculated by
where dist(x,y) is the Euclidean distance in the objective space.
Then, the second proportion of the population for the next generation P2is selected (Lines 10-17).The second proportion contains feasible solutions in a relaxed manner.The relaxation factorεis calculated as
whereCVmaxis the maximum CV found by the population so far;gis the current generation;Gmaxis the maximum generation, andηis a parameter to control the reducing speed ofε.In this equation, only one parameterηis used.It is set to 2, and the effectiveness ofηwill be studied in the experiments.The design ofεincludes the following underlying considerations.UsingCVmaxfound so far can guarantee a large enough initial value ofε.As the evolution proceeds,reduces from 1 to 0.Moreover, η=2 generates a gradually decreasing gradient ofεrelated to.Therefore, at the earlier stage,εreduces faster, while at the latter stage,εreduces slower.Therefore, at the earlier stage,εis a large value to produce a better exploration of feasible regions.Then, at the latter stage,εis a small value closer to 0 to ensure the exploitation of feasible regions.With a relaxation factor, all solutions that have a CV value no more thanεare preselected (Lines 10-12).Also,redundant solutions with low diversity are deleted (Lines 13-17).Finally, the closest distance values of P1and the CV values of P2are used for mating selections (Lines 19 and 20).

Algorithm 2 Even Search Require: N (required size), (candidate solution set), (obtained feasible solution set), g (current generation), (maximum constraint violation found so far)P FP1 FP2 S F CVmax Output: (population for next generation), (fitness values of first proportion of population), (fitness values of second proportion of population)PR ← P 1: Determine whether solutions of are in promising region by Algorithm 1;S ← PR=1 2: Preselect solutions satisfy ;F ← S 3: Perform fast non-dominated sorting on ;P1 ← S F=1 4: Select solutions in that satisfy ;|P1|>N 5: while do D ←6: Calculate the closest distance between each solution to its closest solution using (4);x=argminx∈P1 Dx 7: ;8: Delete solution x with minimum closest distance;9: end while ε ←10: Update the value of ε using (5);CV ←S 11: Calculate the constraint violation values of solutions in;P2 ← S CV ≤ε 12: Select solutions in that satisfy ;|P2|>N 13: while do D ←14: Calculate the closest distance between each solution to its closest solution using (4);x=argminx∈P1 Dx 15: ;16: Delete solution x with minimum closest distance;17: end while P ←P1 ∪P2 18:-FP1 ← P1 19: The closest distance values of ;FP2 ← P2 20: The constraint violation values of ;P 21: return
The benefits of using these two kinds of solutions can be illustrated in Fig.3.As shown in Fig.3(a), darker diamonds located on the UPF are preferred, so they could accelerate the approximation to the CPF and help to jump out of local feasible regions.If the UPF overlaps with the CPF, P1could even help to find feasible solutions on the CPF.As shown in Fig.3(b), darker triangles are preferred.Therefore, those solutions near, or even in, the detected or undetected feasible regions could be preserved.They could help to search the detected feasible regions and detect new feasible regions.
The reasons for developing such a method are as follows.First, an unknown CMOP might have a very large objective space, as well as a large promising region, so we have to further limit the even search to a smaller region.That is to say,we have to design some rules that preserve valuable, rather than all, solutions in the promising region.Second, the preferred two kinds of solutions are both useful for detecting and searching the CPF.Third, in order to avoid overfitting, we make these rules very simple and extensible.
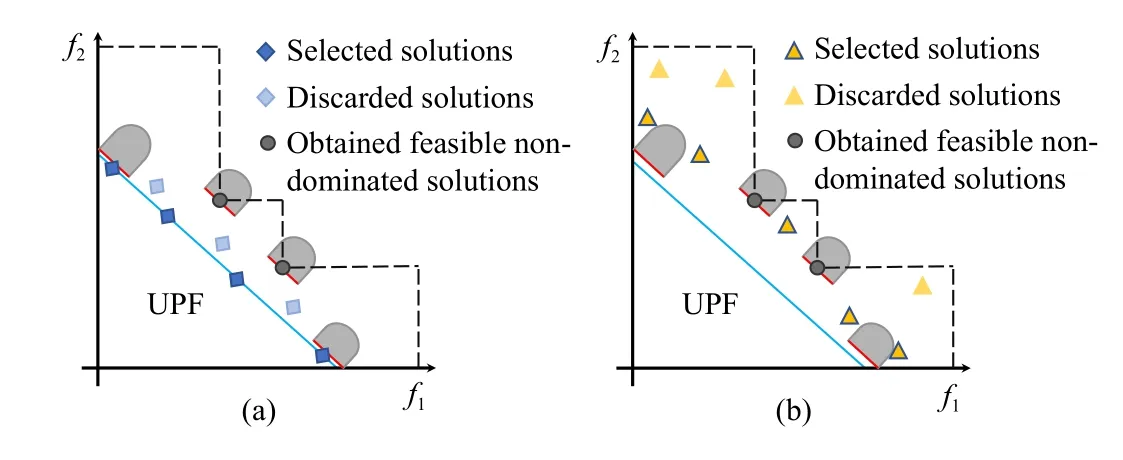
Fig.3.An illustration of the benefits of the proposed even search method.In Fig.3(a), the darker diamond solutions are preserved to accelerate the convergence and jump out of local feasible regions; in Fig.3(b), the darker triangles are preserved to detect feasible regions.
C. Mating Selection
In this part, we introduce the mating selection method based on the tournament selection mechanism.The pseudo code is presented in Algorithm 3.As mentioned in the last part, we output -FP1and FP2as the criteria used in the mating selections of P1and P2, respectively.Therefore, in the mating selection of P1, we select the solution with a larger closest distance from two randomly selected solutions each time, until the size of the mating pool reachesN.Similarly, for P2, we select the solution with a smaller CV value from two each time until the size of the mating pool reachesN.

Algorithm 3 Mating Selection Based on Tournament P Require: N (required size), (candidate solution set), F (fitness criteria)M Output: (selected mating pool)M ←∅1: ;|M|≤N 2: while do x,y ← P 3: Randomly select two solution from ;Fx >Fy 4: if then M ←M∪y 5: ;Fx <Fy 6: els if then M ←M∪x 7: ;8: else M ← M 9: Randomly add x or y to ;10: end if 11: endw hile M 12: return
Selecting non-dominated solutions with better diversity as mating parents could improve the search near the UPF.Also,selecting relaxed feasible solutions with smaller CV values as mating parents could enhance the search for feasible regions.Besides, the Tournament Selection mechanism that uses two randomly selected solutions each time could enhance the possibility that worse solutions might also be selected, so the exploration ability could be enhanced.
D. Update the Archive
In this part, we introduce the method used to update the archive that stores obtained feasible solutions.The pseudo code is presented in Algorithm 4.The archive has two functions.First, it is used to store obtained feasible solutions to determine whether solutions are in the promising region.Second, the archive is used as the final output solution set of CMOES.Therefore, the archive must be updated at each generation and the convergence and diversity of feasible solutions must be enhanced.

Algorithm 4 Update the Archive Require: N (required size), (candidate solution set), (archive at last generation)A FA P A Output: (archive for next generation), (fitness values of archive solutions)FN ←1: Perform the non-dominated sorting using constrained dominance principle in NSGA-II and obtain the front number of each solution in ;A ← P FN=1 A P 2: Add solutions in that satisfy to ;|A|>N 3: if then FA ←4: Calculate the Crowding distance of NSGA-II values of solutions in ;A, FA ←A 5: Delete redundant solutions using the Crowding distance and save the Crowding distance values of preserved solutions;6: end if A, FA 7: return
Based on the above considerations, any update mechanism of any MOEA that balances convergence and diversity could be used.In CMOES, we use the mechanism of NSGA-II, a classical and simple MOEA, for updating the archive.Other mechanisms could also be used as a substitute.In the strategy of this paper, we first include all feasible solutions of the population P.Then, if the size of A exceedsN, the redundant feasible solutions with worse crowding distance values are deleted.
E. The Framework of CMOES
Based on the above methods, we introduce the framework of CMOES.The general procedure of CMOES is presented in the flowchart shown in Fig.4.In order to perform the even search method, we need to first find feasible solutions.Therefore, the proposed CMOES contains two stages.In stage I,CMOES evolves the population by a CMOEA and updates the archive by the obtained feasible solutions.It is worth noting that terminating stage I has two conditions.The first condition indicates that stage II starts when at least one feasible solution is found and stored in A.The second conditiong>θ×Gmaxis designed to allocate more computing resources to push the population to approximate the CPF.Then, in stage II, we generate offspring sets for both the archive and the population.Since the archive contains feasible solutions, we generate offspring using it to better exploit feasible regions.
The pseudocode of CMOES is presented in Algorithm 5.One important point that we should note is the procedure of Lines 12-16.In order to provide criteria for mating selections in stage II, we need to calculate FP1, FP2, and FA at the beginning of stage II.Therefore, we use a flagsto control this step.

Fig.4.The overall framework of the proposed CMOES.

Algorithm 5 The Framework of CMOESPR Require: N (population size), (termination condition), η (evolutionary length for finding feasible solutions)A Gmax Output: (final archive solution set)P ←1: Generate the initial population randomly;CVmax ←2: Calculate the maximum constraint violation of population;A ←3: Update the archive by Algorithm 4;g ←4: Set the current generation zero;s ←5: Set the current search stage zero;g <Gmax 6: while do g ←g+1 7: ;|A|=0||g <η×Gmax 8: if then P ←9: Evolve the population by a CMOEA;A ←10: Update the archive by Algorithm 4;11: else s=0 12: if then s ←1 13: ;FP1,FP2 ←14: Calculate the fitness of two proportions of the population;FA ←15: Calculate the fitness of solutions of the archive;16: end if MA ←FA |A|17: Tournament selection for the mating pool of archive based on with size ;OA ←MA 18: Generate offspring by the GA operator based on;MP1 ←FP1 19: Tournament selection for the mating pool of the first proportion of the population based on ;OP1 ←MP1 20: Generate offspring by the GA operator based on;MP2 ←FP1 21: Tournament selection for the mating pool of the second proportion of the population based on ;OP2 ←MP2 22: Generate offspring by the GA operator based on;O ←OA∪OP1 ∪OP2 23: ;P, FP1, FP2 ←24: Update the population by Algorithm 2;A, FA ←25: Update the archive by Algorithm 4;26: end if CVmax ←27: Update the maximum constraint violation value found by the population;28: end while A 29: return
F. Computational Complexity
The computational complexity of Algorithm 1 isO(mN2)since the maximum size of the archive isN.The computational complexity of Algorithm 2 isO(mN2) for the fast nondominated sorting andO(N)2for calculating the closest distance.The computational complexity of Algorithm 3 isO(N).The computational complexity of Algorithm 4 isO(mN2) of calculating the crowding distance by NSGA-II.In summary,the computational complexity of CMOES isO(mN2).However, as the procedure runs sequentially, the practical time complexity could be several times larger.
G. Remarks
The proposed CMOES is different from existing multistage-based and multi-population-based CMOEAs, which adopt multiple stages and populations with different CHTs or algorithmic strategies.More specifically, CMOES is not a multi-stage-based CMOEA because the former stage is adopted only to ensure that at least one feasible solution is obtained to determine the PR.In addition, CMOES is not a multi-population-based CMOEA because P1and P2are used to maintain two different kinds of promising solutions found in the PR, rather than two populations.
The proposed even search method is also different from theε-constrained technique (constraint relaxation), which ignores constraints (i.e., CV) to some extent through a relaxation factor and prefers solutions with better convergence (i.e., nondominated).In even search, all solutions with a CV value smaller thanε, whether dominated or non-ominated, can survive.In addition, the even search method aims to enhance the distribution of these solutions in the PR to explore the CPF.This can provide a more comprehensive search than the constraint relaxation techniques.
Finally, CMOES is different from the methods in [10], [17],which both use constraint relaxation in one of their components (population and archive).In CMOES, the proposed even search method is adopted.Although CMOES also contains a factorε, it is more simplistic and its function is different.It is used in the even search to determine the second proportion of promising solutions.Comparative studies are conducted and presented in Section IV-F.
IV.EXPERIMENTAL STUDIES
This section presents the experimental studies, including the settings, results, and analysis, on CMOES.All experiments were conducted on PlatEMO [18]3Detailed discussions and analyses on all experimental results can be found in the supplementary file at: https: //wewnyin.github.io/wenyingong/Publication/CMOES-supp.pdf..
A. Experimental Settings
1)CMOPs for Experiments: We selected four benchmarkCMOP test suites and 14 real-world CMOPs to test our proposed CMOES.The four benchmarks include MW [19], LYO[9], LIR-CMOP [20], and DAS-CMOP [21].The 14 realworld test problems are the former 14 two-objective CMOPs from the test suite for the IEEE CEC 2021 Competition on Real-World Multiobjective Constrained Optimization [22]4Dimensions of m and n of the selected benchmarks are reported in Table S-I in the Supplementary file..

TABLE I A SUMMARY OF STATISTICAL RESULTS OF HV AND IGD+ ON ALL BENCHMARK AND REAL-WORLD PROBLEMS
2)CMOEAs for Experiments: In this paper, we selected 11 state-of-the-art CMOEAs for comparison, including methods belonging to all three categories in Section II-B.They are BiCo [23], CMOEA-MS [5], MFO [13] (the MFO-SPEA2 instantiation), ShiP [1] (the ShiP-A instantiation), URCMO[6], C-TAEA [4], CCMO [12], ToP [3], DSPCMDE [14],NSGA-II-ToR [15], and CCEA [9].
3)Parameter Settings and Genetic Operators: For algorithms that use the operators of GA, the simulated binary crossover (SBX) and polynomial mutation (PM) were adopted with the following parameter settings:
a) Crossover probability waspc=1; distribution index was ηc=20;
b) Mutation probability waspm=1/n; distribution index was ηm=20.
For algorithms that use the operators of DE, the parametersCRandFin the DE operator were set to 1 and 0.5, respectively.
The population sizeNwas set to 100, the maximum evaluationEmaxwas100000,themaximumgenerationGmaxwasEmax/N.Thisworkadopts σ=10-4forthetested problems as the relaxation for equality constraints.All other parameter settings of the comparison methods were the same as in their original literature (i.e., the default settings in PlatEMO).The parameters for our proposed methods includeηused to calculateε, it is set to 2 and the influence of this parameter will be studied in Section IV-E.
4)Performance Indicators: Inverted generational distance based on modified distance calculation (IGD+) [24] and hypervolume (HV) [25] were adopted as indicators to evaluate the performance of different algorithms.IGD+ is used because IGD is proved Pareto non complaint [24].We used two indicators to achieve a sound and fair comparison [26].
Suppose Z is a set of uniformly distributed points on CPF and A is the solution set.In IGD+,d(ai,zj) is calculated as
then, IGD+ is calculated as
whered(ai,zj) is the Euclidean distance betweenaandz.
A smaller IGD+ value indicates a better performance.
HV [25] measures the volume or hypervolume of the objective space enclosed by the obtained solution set and the predefined reference point zr, HV of a solution set A can be formulated as
where VOL indicates the Lebesgue measure.A larger HV value indicates better performance obtained.
10 000uniformly distributed points were sampled on the true CPF for the calculation of IGD+ according to [12].As for HV, the objective values were first normalized, and then,(1.1,1.1,...,1.1)was adopted as the reference point in the normalized objective space.
5)Statistical Analysis: Each algorithm executed over independent 30 runs on each test instance.The mean and standard deviation values of IGD+ and HV were recorded.The Wilcoxon rank-sum test with a significance level of 0.05 was employed to perform the statistical analysis.Additionally,“+”, “-” and “=” were used to show that the results of other algorithms were significantly better than, significantly worse than, and statistically similar to those obtained by our methods to the Wilcoxon test, respectively.
B. On Benchmark CMOPs
This part presents the results and analyses of benchmark CMOPs.A short summary of the statistical results is presented in Table I.In the Supplementary file, more detailed explanations and analyses are provided.

Fig.5.The convergence profiles on IGD+ of CMOES and other methods on DAS-CMOP1, LIR-CMOP11, LYO4, and MW11 with the median IGD+ values among 30 runs.
1)On DAS-CMOPs: DAS-CMOPs are featured as adjustable difficulties on convergence, diversity, and feasibility, which tests the versatility and generic ability of an algorithm.The statistical results on HV and IGD+ obtained by CMOES and other CMOEAs are recorded in Tables S-II and S-III in the Supplementary file.The results show that CMOES outperformed all other methods on DAS-CMOP1 to DASCMOP6, while CMOEA-MS, CCMO, URCMO, and CCEA outperformed CMOES on DAS-CMOP7, DAS-CMOP8,DAS-CMOP9, and DAS-CMOP7-8, respectively.The feasible and non-dominated solution sets obtained by CMOES on each instance of DAS-CMOPs with the median IGD+ values among 30 runs are presented in Fig.S-I in the Supplementary file.It is apparent that CMOES had finally found the CPF and achieved good diversity in each instance.To further compare the results, we depicted feasible and non-dominated solution sets obtained by all methods on DAS-CMOP3 and DASCMOP9 in Figs.S-2 and S-3 in the Supplementary file, respectively.It could be found that most of the methods in comparison could not handle these two CMOPs well.Although DSPCMDE could find the CPF of DAS-CMOP3, it performed poorly on DAS-CMOP9.Similarly, although URCMO performed well on DAS-CMOP0, it performed poorly on DAS-CMOP3.However, CMOES could only find most of,not all, the feasible regions on DAS-CMOP7-9, and the diversity performances were not very good.The reason could be that in our update strategy of the archive (which is used as the final output), the crowding distance of NSGA-II was adopted,but it is not very suitable for three-objective problems.In addition, a three-objective space is much larger, and achieving an even search is much harder.Nevertheless, CMOES could solve all instances of DAS-CMOPs, demonstrating that it has the best versatility.Fig.5(a) presents the convergence profile on IGD+ of CMOES and other methods on DASCMOP1.Compared to other methods, CMOES obtained not only fast convergence speed but also the best final IGD+value.

Fig.6.Feasible and non-dominated solution sets obtained by CMOES and other methods on LIR-CMOP8 with the median IGD+ value among 30 runs.(a) Contains the results of BiCo, CMOEA-MS, MFO-SPEA2, ShiP-A, URCMO, and C-TAEA; (b) Contains the results of CCMO, ToP, DSPCMDE, NSGA-IIToR, CCEA, and CMOES.
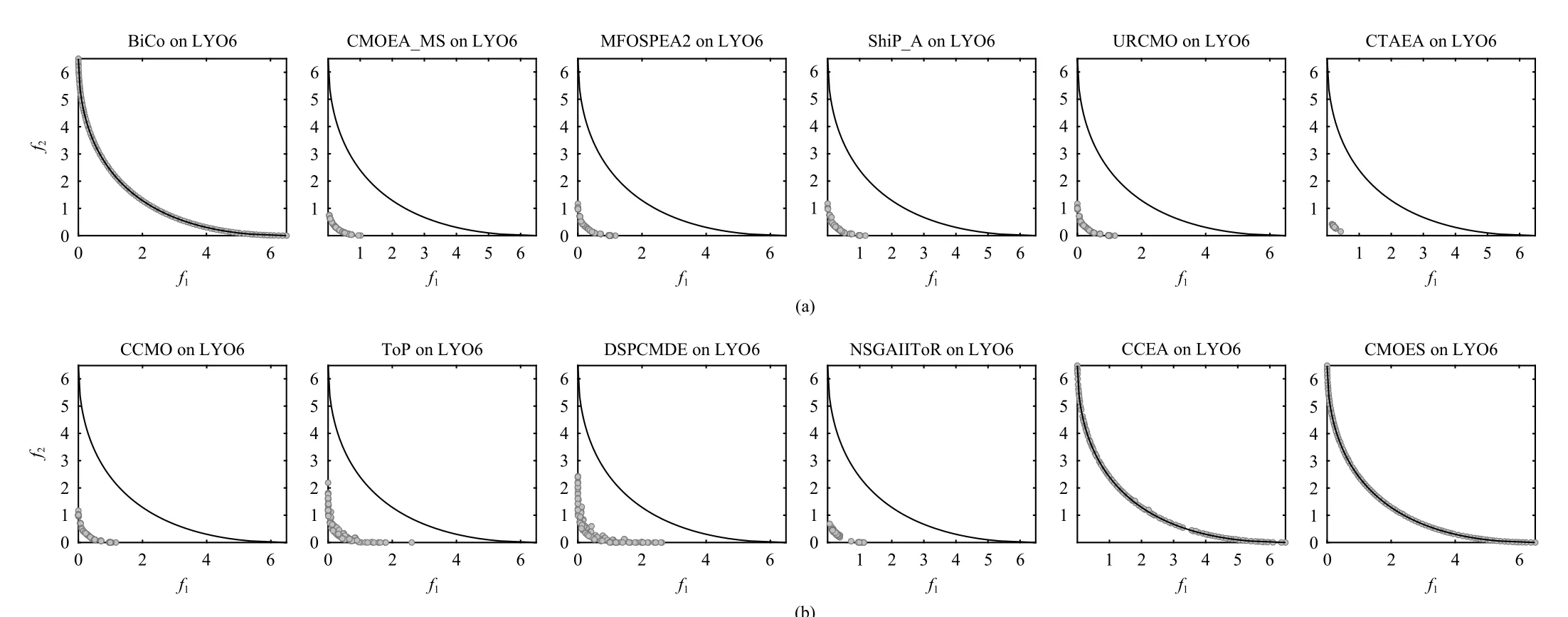
Fig.7.Feasible and non-dominated solution sets obtained by CMOES and other methods on LYO6 with the median IGD+ value among 30 runs.(a) Contains the results of BiCo, CMOEA-MS, MFO-SPEA2, ShiP-A, URCMO, and C-TAEA; (b) Contains the results of CCMO, ToP, DSPCMDE, NSGA-II-ToR, CCEA,and CMOES.
2)On LIR-CMOPs: LIR-CMOPs are featured as large infeasible regions that propose difficulties for an algorithm to locate very feasible regions, especially for those feasibilitypreferred CMOEAs.Tables S-IV and S-V in the Supplementary file present the statistical results on HV and IGD+obtained by CMOES and other methods, respectively.The results show that ShiP-A performed better than CMOES on LIR-CMOP1-4, DSPCMDE performed better on LIRCMOP5-6 and LIR-CMOP7, and some CMOEAs performed better on LIR-CMOP13-14.For three-objective LIRCMOP13-14, the reasons are the same.To further investigate the results, we depicted the feasible and non-dominated solution sets obtained by CMOES on each instance of LIRCMOPs with the median IGD+ values among 30 runs in Fig.S-4 in the Supplementary file.Also, we depicted the feasible and non-dominated solution sets obtained by all methods in Fig.6.It is apparent that CMOES had found only some parts of the CPF on LIR-CMOP1-4 and the better indicator results on LIR-CMOP5-10 were because CMOES could find the CPF impeded by the large infeasible regions.Although CMOES outperformed most of the methods in comparison,these results reveal that the effectiveness of CMOES in dealing with CMOPs with very small feasible regions has to be improved.In summary, CMOES could handle LIR-CMOPs with large infeasible regions because the even search method could explore the objective space where the small feasible regions locate.Fig.5(b) presents the convergence profile on IGD+ of CMOES and other methods on LIR-CMOP11.Compared to other methods, CMOES obtained the best final IGD+value.
3)On LYOs: LYOs are a set of special benchmark CMOPs that the initial population arises in the complex infeasible regions below the CPF in the objective space.Therefore, it proposes difficulties for an algorithm to make use of infeasible solutions to search back to the CPF.The statistical results on HV and IGD+ obtained by CMOES and other CMOEAs are reported in Tables S-VI and S-VII in the Supplementary file.CCEA and CMOES obtained the best overall results,except that only URCMO performed better on LYO2.Most CMOEAs in comparison could not handle LYO5-8, except for CCEA and CMOES.However, CMOES performed worse than CCEA, an algorithm proposed for the LYOs.To further analyze the results, we depicted the obtained final solution sets by CMOES on all instances with the median IGD+ values among 30 runs in Fig.S-6 in the Supplementary file, and the obtained solution sets by all methods on LYO6 in Fig.7.From Fig.7 we can see that only BiCo, CCEA, and CMOES could find the CPF.From Fig.S-6 in the Supplementary file it can be found that CMOES could not find all the segments of the CPF on LYO7-8.Since the distribution of feasible and infeasible regions was not given in LYO, it can be only inferred that the reason is few or no offspring could be generated in the sparse and blank areas when dealing with LYO7-8.Nevertheless, CMOES performed well on this special test suite compared to most state-of-the-art CMOEAs, demonstrating the effectiveness of CMOES in using valuable solutions in the promising region.Fig.5(c) presents the convergence profile on IGD+ of CMOES and other methods on LYO4.Compared to other methods, CMOES obtained the best final IGD+value.Additionally, the extremely bad performances of CMOEA-MS, MFO-SPEA2, and CCMO also demonstrate that these CMOEAs using a specific or complicated strategy lack versatility.
4)On MWs: MWs are featured as four relationships between the CPF and the UPF, which comprehensively represent the problem types in terms of the position and distribution of the CPF relative to the UPF.However, according to our experimental experience, MWs lack difficulties in the distribution of infeasible regions.Therefore, ignoring constraints could well assist the search for the CPF for most instances of MW, especially the Type-I to Type-III problems.However,these constraint-ignoring-assisted CMOEAs performed worse in dealing with Type-IV problems.Therefore, as the statistical results reported in Tables S-VIII and S-IX in the Supplementary file reflected, those CMOEAs using a constraintignored auxiliary problem (BiCo, CMOEA-MS, MFPSPEA2,and CCMO) performed well.Besides, although MFO-SPEA2 and BiCo performed extremely well on MWs, they also performed extremely poorly on DAS-CMOPs, LIR-CMOPs, and LYOs.This indicates that some advanced approaches lack versatility but overfit some kinds of problems.To further analyze the results, we depicted the obtained final solution sets of CMOES on all instances of MW in Fig.S-8 in the Supplementary file.It can be found that CMOES finally obtained very good results in terms of both convergence and diversity,except that it could not find the CPF segment in a very small feasible region on MW10.Fig.5(d) presents the convergence profile on IGD+ of CMOES and other methods on MW11.It can be found many state-of-the-art CMOEAs could solve this problem very well.
5)Summaries and Conclusions: The results of these four benchmark suites show the following phenomena.BiCo and MFO-SPEA2 performed very well on the MW test suite but extremely poorly on the other three.CCEA performed very well on the LYO test suite but performed poorly on the others.ShiP-A performed very well on LIR-CMOP1-4 but poorly on other instances of LIR-CMOPs, also, it performed well on some Type-I, Type-II, and Type-III instances (MW2, MW6,MW10, and MW13) of MW but performed poorly on others,especially on Type-IV instances.Therefore, these methods are somehow overly fine-tuned and overfitting.As we analyzed above, although CMOES could not achieve the best indicator values, it can find the CPF and obtain good distribution on it in the face of most instances, especially DAS-CMOPs with adjustable and multiple features.It can be concluded that searching in the promising region can achieve the best versatility.
C. On Real-World CMOPs
In this part, we present the experiment on real-world CMOPs.We selected the former 14 two-objective CMOPs from the IEEE CEC 2021 Competition on Real-World Multiobjective Constrained Optimization test suite in this experiment.It should be noted that the features and difficulties of these problems are unknown, and they include CMOPs from very different application fields.Since the true CPFs are unknown, IGD+ is not applicable, so only HV is used.The statistical results of HV are reported in Table S-X in the Supplementary file.It could be seen that CMOES generally outperformed all the other methods except for ToP.Also, they obtained the largest number of best results (four) among these 14 instances.From the results, we could draw the following three conclusions.First, different algorithms perform very differently among various CMOPs.Second, without complex strategies or techniques, CMOES and ToP performed better than those with complex strategies and techniques on realworld problems.Third, although different algorithms performed differently, CMOES generally obtained better versatility.
D. Ablation Studies on the Effectiveness of Even Search
In this part, we present the ablation study conducted to verify the effectiveness of our proposed even search method.First, we created two variants as follows
1)CMOESP1: Only the first proportion of the population is preserved and evolved in mating and selection;
2)CMOESP2: Only the second proportion of the population is preserved and evolved in mating and selection.
The results on HV and IGD+ on the four benchmarks are presented in Tables S-XI-S-XVIII in the Supplementary file.In summary, we could draw the same conclusion as mentioned in Section II-B.Preserving only the first proportion performed better on CMOPs whose CPF is close to or contained by the UPF, on the contrary, preserving only the second proportion performed better on CMOPs whose CPF is far from the UPF, especially LYOs.
Then, we depicted the distributions of the second proportion of the population at the middle stage of evolution (i.e.,Gmax/2) in dealing with DAS-CMOP1, DAS-CMOP5, LIRCMOP1, LIR-CMOP11, LYO1, and MW13 with the median IGD+ values among 30 runs in Fig.8.From these figures, we could see that the second proportion of the population had even distributions near all segments of the CPF on DASCMOP1 and DAS-CMOP5.Also, it covered the most promising regions that contain the CPF on LIR-CMOP1 and LIRCMOP11.It should be noted that LIR-CMOP1 is rather difficult due to the very small feasible region (long and thin line).It reached the CPF from several directions and finally found all segments of the CPF on LYO1.It also had good distribution near all regions that the CPF is in on MW13, includingf1∈[0,1], the CPF segments covered by very small feasible regions.In summary, the second proportion of the population could cover most of the CPF segments and help to detect new feasible regions in dealing with these CMOPs with very different features and challenges, revealing that our proposed even search method is versatile and robust.
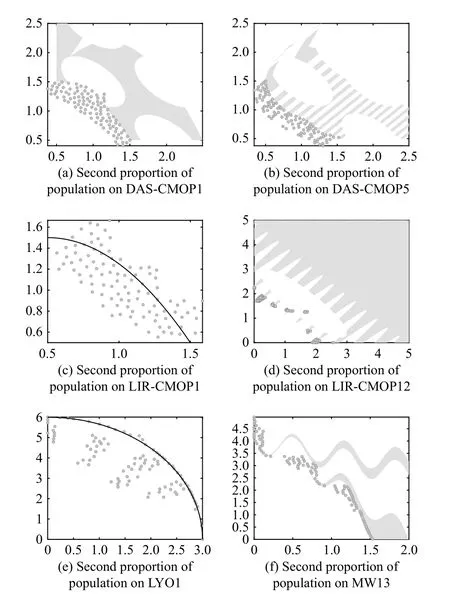
Fig.8.The distributions of the second proportion of the population at the middle stage of evolution in dealing with DAS-CMOP1, DAS-CMOP5, LIRCMOP1, LIR-CMOP11, LYO1, and MW13 with the median IGD+ values among 30 runs.
Therefore, from the above results and analysis, we have demonstrated the effectiveness of the proposed even search method.The first proportion of the population could enhance the convergence and suit some kinds of CMOPs, while the second could help to solve other kinds of CMOPs.
E. Parameter Analyses
Since our proposed methods contain two important parameters,ηused to calculateεandθused to control the length of the former stage, we also conducted experiments on studying the sensitivity of these parameters.Specifically, we changedηto 1/2, 1, 3/2, and 3 respectively, instead of 2 in the original setting, to study the effectiveness of the proposedεunder an incremental (1 /2), steady (1), gently-decreasing (3/2), and rapidly-decreasing (3) gradient.The statistical results on HV and IGD+ on the four benchmarks are presented in Tables SXIX-S-XXVI in the Supplementary file.
For DAS-CMOPs and LIR-CMOPs, η=2 is the most suitable setting for most cases.For LYOs, η=2 and η=3 perform similarly while η =2 has better general performance.For MWs, a largerεis also more suitable for those instances with very small feasible regions (MW2, MW6, MW10, and MW13).However, η=2 is more suitable for LIR-CMOPs.This also demonstrates the announcement that a specified and complicated technique might overfit some problems, and a simple strategy or technique is more applicable for real-world applications.
For DAS-CMOPs, θ=2 is the best setting, For LIRCMOPs, a smallerθresults in a shorter former stage and longer even search stage, bringing better performance on LIRCMOP1-4 which has the smallest feasible region, revealing that our proposed even search strategy can enhance the performance when the feasible regions are considerably small.The setting ofθdoes not have a significant influence on LYOs and MWs.
F. Comparison With Constraint Relaxation-Based CMOEAs
In this part, the proposed CMOES is compared to the constraint relaxation-based CMOEAS in TriP [10] and PPTA [17]to prove the superiority of even search.HV and IGD+ results on benchmark problems are reported in Table S-XXVII in the Supplementary file.Trip and PPTA outperformed CMOES only on LIR-CMOP1-6, whose feasible regions are considerably small.Similarly, TriP can only outperform CMOES on MW instances with very small feasible regions.Meanwhile,CMOES outperformed them in almost all the other instances,from which the following two observations can be made.Trip and PPTA both adopt a fine-tunedε-constrained technique,which can enhance the performance on several special instances but fail to adapt to different kinds of problems.On the contrary, CMOES, which uses only simplistic designed techniques and a general even search method, has better versatility.
V.CONCLUSIONS AND FUTURE WORK
In this article, we proposed to search evenly in the promising region to solve CMOPs.We investigated that the promising region contains the CPF and has good properties.Then,we designed an even search method that utilizes two kinds of valuable solutions to search evenly in the promising region for the CPF.A new CMOEA, termed CMOES, is developed based on simple strategies and techniques, and the experiments have demonstrated the effectiveness and the best versatility of our proposed methods on both benchmark and realworld CMOPs.The results prove that a specified, especially complicated, strategy or technique might overfit some problems with specific properties, resulting in a lack of versatility.On the contrary, methods that use simple strategies and techniques could be more applicable to real-world problems whose features and difficulties are unknown.
However, the proposed CMOES also has some limitations that need to be improved.The ineffectiveness of the proposed CMOES on LYO7-8 needs further investigation.It indicates that the proposedε-constrained technique is still sensitive to the parameters and design.Besides, how to better locate feasible regions while searching evenly in the promising region is expected referring to Fig.8(f), especially when dealing with CMOPs with very small feasible regions.Furthermore, using machine learning techniques to achieve an even search in the promising region is worth trying [27]-[29].Last but not least,extending the even search method to other types of multiobjective optimization problems to enhance the performances of existing algorithms is also valuable [30], [31].
The codes of CMOES can be obtained from the authors upon request.
 IEEE/CAA Journal of Automatica Sinica2024年2期
IEEE/CAA Journal of Automatica Sinica2024年2期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Reinforcement Learning in Process Industries:Review and Perspective
- Communication Resource-Efficient Vehicle Platooning Control With Various Spacing Policies
- Virtual Power Plants for Grid Resilience: A Concise Overview of Research and Applications
- Equilibrium Strategy of the Pursuit-Evasion Game in Three-Dimensional Space
- Robust Distributed Model Predictive Control for Formation Tracking of Nonholonomic Vehicles
- Stabilization With Prescribed Instant via Lyapunov Method
