智能消杀机器人路径规划与滑模跟踪算法研究
梁凤强,陈晓杰,韩铭雪
(国网临沂供电公司,山东 临沂 270000)
0 引言
非完整移动机器人是集环境感知、动态决策和行为控制于一体的复杂系统。近年来,非完整移动机器人控制受到业界的密切关注,相关产品和技术广泛应用于室内鸟瞰图的构建、野外道路环境调查和自动货物装卸等场合[1-3]。本文开展了基于A-star 算法的机器人连续积分滑模路径跟踪控制研究。首先,采用A-star 路径规划算法,实现移动机器人的全局快速路径规划,从而得到最优的机器人运动路径。然后,根据输出路径,设计分段连续积分滑模跟踪控制器,该控制器有效地提高了系统的趋近速率,实现跟踪误差在有限时间内趋近于零,保证了路径跟踪精度和控制系统的稳定性。最后,通过仿真实验验证了方法的有效性。
1 现状
文献[4]在移动机器人中引入模糊控制方法,提高了系统的控制精度。文献[5-7]提及滑模控制具有良好的稳健性,需要解决滑模面设计过程中固有的抖动问题。文献[8]采用A-star算法规划机器人的室内运动。文献[9-11]采用自适应模糊控制提高了机器人系统的稳健性。文献[12-14]采用了神经网络自适应控制方法,实现移动机器人较小的跟踪误差和较强的抗干扰能力。
移动机器人普遍存在约束问题,文献[15]提出的自适应控制方法成功地处理了约束。文献[16]为机器人电机的安全性增加了电流饱和约束、路径偏差和速度跟踪约束,保证机器人的稳定性。此外,文献[17-19]设计了路径跟踪自适应控制算法,机器人跟踪误差收敛到足够小的量。
2 路径规划
A-star 算法是在二维环境下进行路径规划的算法,具有简单、快速的特点。在路径搜索时,针对实际问题制定相应的启发式函数进行引导性搜索,达到减少搜索节点的目的,提高路径搜索效率。
A-star 算法结合了Dijkstra 算法和最优快速搜索算法,机器人在找到最优路径的同时,计算量较小。算法设计如下:
式中,g(n) 为节点N到起始点的移动代价;f(n) 为第n个节点的综合优先级,算法根据节点的优先级选择下一个待遍历的节点;h(n)为节点N到终点的期望代价,为快速优先算法的启发式函数。
启发式函数h(n)在A-star 算法中至关重要。在极端情况下,如果h(n)为0,函数f(n)中仅有g(n)发挥作用,A-star 算法变化为Dijkstra算法。h(n)越小,A-star 算法遍历节点越多,算法运行速度越慢。反之,h(n)越大,A-star就会成为快速优先算法。
启发式函数用以下方法计算:
该形式的启发函数可以计算直线距离和对角线距离,完整的算法包含初始化开集和闭集;将初始点放入开集,设优先级为最高;如果开集不为空,则从开集中选择优先级最高的节点为节点N。
如果节点N是目标节点,则完成路径规划,跟踪父节点从终点到起点。如果节点N不是目标节点,将节点N从开集中移除,置于闭集中,遍历节点N周围的所有节点。
如果与N相邻的节点M在闭集中,则跳过并检测下一个节点。如果节点M不在开集中,将M的父节点设为N,计算M的优先级,将节点M加入开集。
如果节点M在开集中,计算比较移动代价f(n)的值,如果f(n)更小,则该节点为父节点,重新计算该值。
3 跟踪方法
3.1 运动学模型
移动机器人状态示意图如图1 所示。机器人位姿(位置和方向)由向量P=[x y θ]Τ表示;运动速度矢量由向量q=[ν ω]Τ表示。其中[x y]为移动机器人的位置,θ为移动机器人前进方向与x轴的夹角,ν和ω分别为移动机器人的线速度和角速度,在运动学模型中作为控制输入。
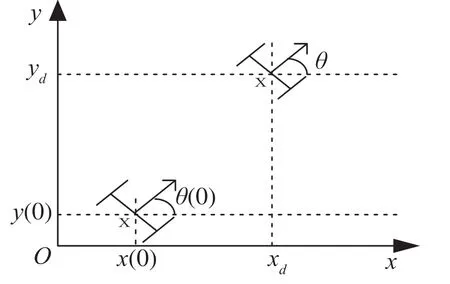
图1 移动机器人状态示意图
考虑移动机器人的运动学方程为:
由运动学方程可以得知,共有2 个自由度,模型输出为3 个变量,该模型为欠驱动系统,只能实现2 个变量的主动跟踪,剩余变量为随动或镇定状态。通过设计控制律q=[ν ω]实现移动机器人位置[x y]的跟踪,实现夹角的随动。得到移动机器人运动学模型为:
3.2 位置滑模控制律设计
通过设计位置控制律ν,实现x跟踪xd,y跟踪yd。取理想路径为[xd yd],则误差跟踪方程为:
控制律根据李雅普诺夫稳定条件确定,构造如下 Lyapunov 函数:
对上式求导可得:
设计控制律为
因此,系统状态将以有限时间到达滑模面,沿滑模面运动,跟踪误差收敛到零。
控制律可根据李雅普诺夫稳定条件确定,构造如下 Lyapunov 函数:
对上式求导可得:
设计控制律为:
因此,系统状态将以有限时间到达滑模面,沿滑模面运动, 跟踪误差收敛到0。
由式(6)可得:
如果θ的值域为则可得到满足理想路径跟踪的θ为:
上式求得的θ为位置控制律式所要求的角度,如果θ与θd相等,则理想的路径控制律可以实现。但是,实际模型式中的θ与θd不可能完全一致,尤其是控制的初始阶段,这会造成闭环跟踪系统式的不稳定。
为此,需要将式(20)求得角度θ当成理想值,取
设计理想的位姿指令[xd yd]时,需要使θd的值域满足
实际的θ与θd之间的差异会造成位置控制律式(11)和式(17)无法精确实现,从而造成闭环系统不稳定。较简单的解决方法是设计相比位置控制收敛更快的姿态控制算法,使θ尽快跟踪θd。
由式(6),可得到实际的位置控制律为:
2.3 姿态滑模控制律设计
设计姿态控制律ω,实现角度θ跟踪θd。
取θc=θ-θd,设计连续积分滑模函数为:
控制律可根据李雅普诺夫稳定条件确定,构造如下 Lyapunov 函数:
对上式求导可得:
设计控制律为:
因此,系统状态将以有限时间到达滑模面,并沿滑模面运动,跟踪误差将收敛到零。
上述的闭环系统属于内外环构成的控制系统,位置子系统为外环,姿态子系统为内环,外环产生中间指令信号传递给内环系统,内环则通过滑模控制律实现对中间指令信号的跟踪。
在控制律式(27)中,需要对外环产生的中间指令信号θd求导,求导较为复杂,为简单起见,采用线性二阶微分器实现。
式中,x(t)为待微分的输入信号;m1为对信号的跟踪变量;m2为信号一阶导数的估计;微分器的初始值为m1(0)=0,m2(0)=0。
4 仿真实验
4.1 路径规划算法
为了验证A-star 算法在路径规划方面的优势和有效性,通过MATLAB 仿真软件将A-star和Dijkstra 路径算法进行了对比。对比实验结果如图2 所示。
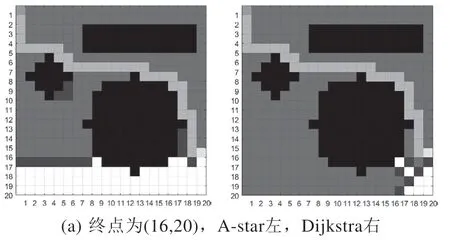

图2 对比实验结果
从图2 中可以看出,相比于Dijkstra 算法,A-star 搜索栅格更少,因此其搜索速度也更快。
4.2 路径规划仿真
为了验证A-star 算法在路径规划上的实用性,采用智能消杀机器人作为验证平台。机器人上装载了激光雷达扫描,树莓派3 以及32位MCU。通过MCU 输出PWM 控制驱动电机运动和转弯,树莓派处理数据进行地图建模。A-star 算法设计路径后,机器人通过设定的控制率循迹运行,即跟踪控制系统的体现。
实验中,机器人稳定运行躲过墙体障碍物,20 s 后准确达到目标位置。A-star 算法循迹图如图3 所示。

图3 A-star算法循迹图
4.3 路径跟踪仿真
为了验证设计的控制器使系统在满足全状态约束条件下,其各状态能够有效跟随给定的参考信号变化,在MATLABSimulink 中搭建仿真实验模型。选取控制参数:c1=c2=c3=5,γ1=γ2=γ3=2,ρ1=ρ2=ρ3=1。
A-star 算法计算的参考信号:yd=[sin(0.5x)+0.5x+1],期望路径的初始位姿为(-2, 2 0) ,进行系统仿真。机器人轨迹跟踪曲线如图4所示。
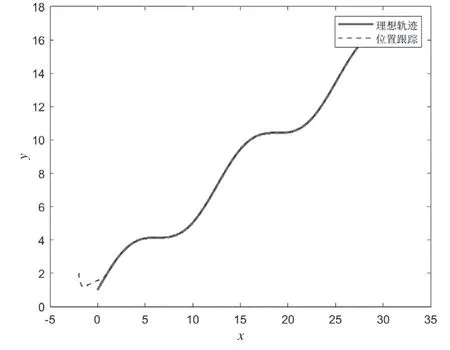
图4 机器人轨迹跟踪曲线
由图4 可以看出,基于本文中所述的运动学模型和连续积分滑模路径跟踪控制器,移动机器人具备良好的跟踪性能,可以在较大的初始误差情况下,确保在较短的时间内实现对期望路径的完全跟踪。同时,系统的抖振现象显著削弱,达到了预期的效果。从图5、图6、图7 中可以看到,机器人位置和角度状态较快地跟踪到参考信号。
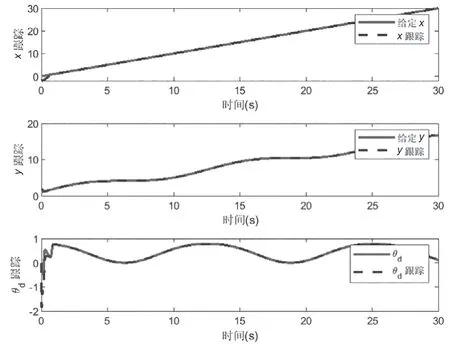
图7 机器人位置和角度跟踪曲线

图8 微分器的输入输出

图9 控制输入信号
5 结语
本文主要开展了基于A-star 算法的机器人连续积分滑模路径跟踪控制研究。为了实现机器人的快速路径规划,采用了A-star 路径规划算法,得到移动机器人所需的最优运动路径。基于规划输出路径,设计了分段连续积分滑模跟踪控制器,实现了位置和姿态的跟踪误差在有限时间内趋近于零,有效地保证路径跟踪精度,通过李雅普诺夫函数证明了控制系统的稳定性。

