高温磁流体动密封结构散热特性分析与优化

张 琛，刘金华，谢 鑫，袁诗咏，汤迎红，米承继，邓英剑，张 灵

（湖南工业大学 机械工程学院，湖南 株洲 412007）

1 研究背景

磁流体于20 世纪60 年代问世，主要被用于真空密封环境，因其具有密封性好、无泄漏、寿命长、无方向性密封、可靠性高及基本无污染等优点而被广泛应用[1-3]。发展至今，磁流体密封技术已经被广泛应用于反应釜、航空航天、单晶炉、真空热处理炉和光伏设备等多个领域。

国内外的学者们已经对磁流体密封结构做了多项研究。Liu S. J.等[4]分析了4 种不同真空磁流体密封装置的优缺点，为磁流体密封结构的设计和分析提供了参考。朱维兵等[5]对离心压缩机磁流体密封结构进行了设计与优化，优化其密封性能，优化的尺寸可为高速旋转轴磁流体密封设计提供参考。Yuan F.等[6]对斜齿径向磁流体密封结构的密封能力进行了研究，提出了一种径向斜齿的轴向-径向双向磁流体密封结构来提高密封性能，结果表明，较小角度的斜齿角度可使磁流体区域有较高的耐压性能，而且还有较低的压降和气体流速。Zhang T.等[7]研究发现磁流体密封的失效压力受永磁材料的影响，且得知磁流体密封的失效压力和永磁体最大磁能积成正比；在这之后，与之成反比。Chen F.等[8]研究了工程机械液压缸磁流体密封磁路，并对其进行了有限元分析，设计了一种八磁源均匀极片结构，结果表明，该磁路结构设计方法合理可行，对磁流体密封设计具有重要的参考意义。程杰等[9]研究了极齿关键参数对磁流体密封热特性的影响，通过研究表明，在一定范围内适当增加密封间隙和极齿高度、适当减小极齿宽度，可以减小磁流体的发热量。Guo Y. Q. 等[10]对大直径磁流体密封结构进行了研究，对磁性液体密封的低温启动力矩和高温耐压性能进行了实验研究,得到了磁性液体的最佳注入量。Yu W. J.等[11]研究了磁性液体蒸发对密封性能的影响，结果表明，蒸发在一定程度上增加了耐压能力，提高了密封性能。Y. Mitamura 等[12]对安装在植入式旋转泵中的微型磁流体密封进行了热分析，当传热系数大于500 时，温升引起的磁化强度降低可忽略不计；温升主要源于电机的热流，而由黏性摩擦产生的温升较小。Hao D.等[13]对高/低温度下大直径磁流体密封特性进行了理论分析与实验研究，实验结果表明，高温下磁性液体饱和磁化强度降低会导致耐压能力下降，低温下磁性液体黏度增大是导致分离力矩变大的关键因素。Yao Y.等[14]研究了热膨胀对磁流体密封性能的影响，数值结果表明,不同转速下流体温度和密封间隙发生变化,从而影响密封性能。李新锐等[15]对大轴径磁流体真空动密封装置进行了优化设计，结果得出楔形极靴聚磁效果更好，饱和磁化强度高，密封能力强，密封的耐压性和耐久性均与间隙呈负相关。Liu J.W.等[16]对环形磁流体密封的密封能力进行了分析以及结构优化，提出了轴向磁化开槽环形磁体磁性液体密封和径向磁化环形磁体磁性液体密封的新结构，结构表面均表现出一定的密封能力。

以上研究有对基本结构尺寸的分析与设计，进而改善结构的密封性和耐压性；也有一些研究了关键参数对热特性产生的影响，研究高温对结构的密封性和耐压性的影响；还有一些是对结构进行优化设计来优化耐压性和密封性；但是目前对其散热特性的研究较少，磁流体的工作温度是有上限的，高温环境中很容易使磁流体失效，改善基本结构尺寸或是关键参数，但很难大幅降低其工作温度，一些对结构优化的研究也没有讨论温度所产生的影响。因此，本文拟通过有限元分析方法对高温磁流体动密封结构的散热特性进行工作温度的分析与结构优化设计，采用数值模拟方法对密封结构的温度、压力和流速进行分析，并将结果与结构优化前的温度、压力及流速进行对比，以证明优化设计的可行性。

2 某型高温磁流体数值模型建立

2.1 计算流体力学

计算流体力学，其内容包含有很多学科。随着该方法现世，现已经可以在一定程度上将一些和流体相关的物理现象定性并量化分析[17]。CFD 模拟通过计算机求解对应模型的数值解，所以被广泛应用于各种工程技术领域[18]。由于某些化学反应较为复杂，如燃烧，想要用实验验证比较困难，且实验真实结果不易获得，以及设备和环境等因素会对实验结果产生较大的影响，此时CFD 的优势便可体现。

2.2 数值模拟理论

图1 是数值模拟计算的一般步骤。

图1 数值模拟计算流程图Fig. 1 Numerical simulation calculation flowchart

2.2.1 基本控制方程

磁流体动密封结构研究所用到的流体力学3 个基础方程为连续性方程、动量守恒方程和能量守恒方程。3 种方程分别由物质守恒定律、能量守恒定律和牛顿第二定律演化而来，但是一些因素会制约这些方程，会限制其使用条件，并不能很好地解决工程上相关的实际问题，此时就要用到湍流模型。

2.2.2 湍流模型

湍流现象：速度很小时，流体能分层运动，层与层之间互不渗透，阻力最小，为层流；当速度增加很大时，流体的流线就会变得很乱无序，相邻层会混合在一起，层流被打乱，这时的流动称为湍流或紊流[19]。这种流动状态的改变可用雷诺数Re来量化，计算公式如式（1）所示，当Re大于4 000 时的流体形态叫做湍流；其值越大湍流强度越剧烈[20]。

式中：ρ为流体密度；v为流体速度；d为特征长度；μ为黏性系数。

湍流是目前较为常见的流动状态，Fluent 中有多种湍流模型可供选择。因为直接数值模拟受相关计算资源影响较大，现实应用极少。非直接数值模拟对N-S方程作了相关简化，常用的模型包括[21]：k-ε、k-ω、k-τ。具体分类如图2 所示。

图2 湍流模型的分类Fig. 2 Classification of turbulence models

标准k-ε模型包含湍动能k和湍动能耗散率ε的方程，工程中使用最多，如式（2）和（3）[22]：

式中：i和j分别为x、y和z各方向的坐标分量；ui为x、y、z方向的速度矢量；Ek为平均速率所引起的湍动能；Eb为浮力产生的湍动能；Yn为可压缩湍流中对总耗能的影响；μt为湍流黏度系数；D1ε、D2ε、D3ε为经验常数，且D1ε=1.44，D2ε=1.92，D3ε= 0.09Sk，其中，S为经验常数；Rε为用户设置的源项。

Realizablek-ε模型公式补充了曲率与转动，ε方程中引申项未涵盖Ek。该模型考虑了旋转运动的影响，可以用于剪切流动、管内流动和分离流等情形。分离层和边界层计算结果尤其可信，但此模型在旋转和静止都具备的环境下误差较大，此时并不适用。

RNGk-ε模型把相关项实施局部调整，在紊流运动时形成的小尺度作用被足够考虑，提高了高速流动的准确性及漩涡流动的精度，因此在广泛流动中比标准模型更可靠。

在RNGk-ε模型中湍流黏性系数可由式（4）计算：

式中Cv≈100。

此模型与标准k-ε显著不同处在于额外项Lε：

式中：η0=4.38；β=0.012；η=Sk/ε。

3 两种热源条件下高温磁流体动密封结构热场分析

3.1 结构和热源条件

某型高温磁流体动密封装置安装在石墨烯反应釜上，该装置通过自身法兰装置与反应釜顶部法兰相连接，搅拌轴贯穿该装置中心圆柱孔并伸入反应釜内。据在现场的工人师傅提供的信息：1）该反应釜在工作时仅需两种温度工况，分别为700, 500 ℃，两种温度工况皆通过反应釜直接设置；2）为确保工作温度的准确性，还会在反应釜工况稳定的情况下通过高温温度计在磁流体动密封装置靠近热源的位置处测量其温度；3）冷却水入水口的流速设置为10 m/s；4）该结构在使用之前会对其进行气密性和温度检测实验，现有气密性实验如图3 所示。通过实验获知，该结构能够达到密封要求；此结构外壳的上表面设置有温度检测孔，通过高温温度计和该孔测得该结构磁流体域内圈正常工作最大温度为299 ℃，极端工况下最大温度为445 ℃。

图3 气密性实验Fig. 3 Air tightness experiment

首先，使用SolidWorks 三维建模软件对某型高温磁流体动密封装置进行建模，因一些零件、圆形孔和一些细小的结构对该仿真分析影响较小，因此同化一部分零件，删去一部分孔类和细小结构，最终的简化模型如图4 所示。

图4 某型高温磁流体动密封装置简化三维模型Fig. 4 Simplified three-dimensional model of a certain type of high-temperature magnetic fluid dynamio sealing device

然后，根据材料和一些需要设置的边界条件划分为磁流体域、实体域和水流域3 个部分，其材料分别为2cr13、304 和水；再通过ANSYS WorkBench 软件对整个结构进行网格划分，所有部分皆使用四面体网格，因水流域部分采用湍流模型，所以要在水流域添加边界层网格，如图5 和图6 所示。

图5 模型网格划分Fig. 5 Model meshing

图6 内部结构水管剖切面截面图Fig. 6 Sectional view of the water pipe internal structure

最后，确定所需的边界条件。由前文可知，该装置的右端面与法兰接触相连，装置中心圆柱内表面与搅拌轴接触连接，通过反应釜腔体内部温度的传递，在有限元分析时，将这两个面定义为热源面。如图6所示，将该模型圆柱孔的内表面（A面）设为第一热源面，将右端面（B面）设为第二热源面。因该结构有两种温度工况，所以需要进行两次有限元分析。第一次分析要为A面和B面同时施加第一种热源温度，为700 ℃；第二次分析为同时施加第二种热源温度，为500 ℃。设置入水口的流速为10 m/s，出水口的压力为0 Pa。

3.2 仿真分析结果

定义水流域入水口的流速为10 m/s，并为热源面A面、B面处分两次施加两种热源：第一次为同时施加700 ℃，第二次为同时施加500 ℃；水作为该结构的流体介质；在水管剖切面定义输出结果场，并通过WorkBench 计算温度场、压力场和速度场；其中网格数量为420 万，计算时间为50 h。

3.2.1 总体域温度场

分别对总体域施加两种热源进行流-热耦合仿真，观察并分析总体域在水管剖切面的两种温度云图，具体结果如图7 所示。由图7 可知，将热源温度设置为700 ℃时，水流域及其附近温度在25～50 ℃的范围，在此外的其他区域，位置越靠近热源其温度越高，平均温度为400 ℃左右；将热源温度设置为500 ℃时，水流域及附近温度也在25～50℃的范围，平均温度为310 ℃左右。

图7 总体域两种热源下水管剖切面温度场Fig. 7 Temperature field in the global domain of the water pipe section of two heat sources

3.2.2 磁流体域温度场

磁流体分布在磁流体域的外表面，磁流体域在两种热源条件下水管剖切面的温度场如图8 所示。

图8 磁流体域两种热源下水管剖切面温度场Fig. 8 Temperature field in the section area of MHD water tubes of two heat sources

由图8 可知，热源温度为700 ℃时磁流体域最高温度为453 ℃，其附近温度为210～230 ℃；热源温度为500 ℃时最高温度为305 ℃，附近温度为109～135 ℃；仿真温度和实验温度比较吻合。而磁流体工作温度不能高于100 ℃，因此，此散热结构有待改进。

3.2.3 实体域温度场

实体域与外部热源相接触，在两种热源条件下水管剖切面的温度场如图9 所示。

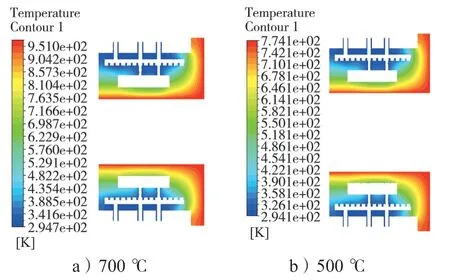
图9 实体域两种热源下水管剖切面温度场Fig. 9 Temperature field in solid domain of the water pipe section of two heat sources

由图9 可知，当热源温度在700 ℃时，靠近热源的区域平均温度为610 ℃左右，在水流域附近的温度为90 ℃左右；当热源温度为500 ℃时热源附近的平均温度为407 ℃左右，水流域附近温度为79 ℃左右。因此，有必要在热源处增加散热渠道和面积。

3.2.4 水流域温度场

水流域为冷却液，可以带走绝大部分热量，其在两种热源条件下的水管剖切面温度场如图10 所示。

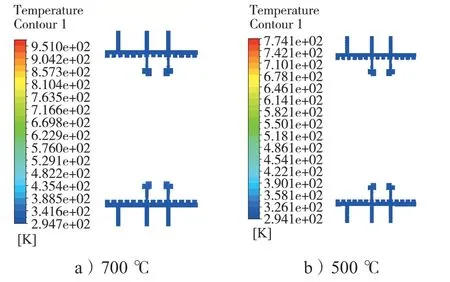
图10 水流域两种热源下水管剖切面温度场Fig. 10 Temperature field of water fluid domain in the water pipe section of two heat sources

由图10 可知，热源温度为700 ℃时，水流域的平均温度为57 ℃左右，最高温度为240 ℃左右；热源温度为500 ℃时，水流域平均温度为48 ℃左右，最高温度为180 ℃左右，充分说明介质水能够较好地带走热量；最高温度出现的位置在热源A面和热源B面交接区域的出水口附近，该位置由于形成了涡流，高温水在此聚集，故形成高温区域。

3.2.5 水流域压力场和速度场

水流域结构为圆柱形和环形的区域，不同的位置压力不同，其在两种热源条件下水管剖切面的压力场如图11 所示。

图11 水流域两种热源下水管剖切面压力场Fig. 11 Pressure field in water fluid domain of the water pipe section of two heat sources

由图11 可知，两种热源的压力场最大值为1.133×105Pa 和1.188×105Pa，即1 个大气压（没有包括外界的大气压），而实际压力场为2 个大气压，约2 kg 压力，出现在入水口附近截面突变位置。

水流域入水口的流速为10 m/s，相同的流速下两种热源条件下水管剖切面的速度场如图12 所示。

图12 水流域两种热源下水管剖切面速度场Fig. 12 Velocity field of water catchment in the pipe section of two heat sources

由图12 可以得知，热源温度为700 ℃和500 ℃时，其水流的最高流速为12.89, 13.25 m/s，出现在出水口截面突变位置。通过两种热源压力场和速度场的仿真分析结果可知，无论温度如何变化，均不会对二者造成影响。

4 高温磁流体动密封结构散热特性改进设计

4.1 优化后的结构和热源条件

根据原始结构的温度场、压力场和流速场的计算结果，提出散热改进方案：一是将水冷的散热区域往右端面延伸；二是在靠近轴热源部位开设隔热气孔，改进后的装置如图13 所示。然后，在同样的热源面即A面和B面施加同样的两种热源温度：一种为同时施加700 ℃，另一种为同时施加500 ℃。

图13 优化后磁流体结构方案Fig. 13 Optimized MHD structure scheme

通过之前的仿真结果得知，速度场和压力场几乎不受温度的影响，因此此次只计算两种热源整个结构的温度场和水流域的压力场，计算压力场可以验证结构的改变是否对水流域的压力产生影响。

4.2 优化后两种热源仿真结果与分析

改进后高温磁流体动密封装置依然设有3 个入水口和3 个出水口，水流速度依然为10 m/s。

4.2.1 磁流体域温度场

结构改进后，磁流体域在两种热源条件下水管剖切面的温度场如图14 所示。

图14 改进后磁流体域两种热源下水管剖切面温度场Fig. 14 Improved temperature field in magnetic fluid domain of the water pipe section of two heat sources

由图14 可以得知，将温度分别设置为700 ℃和500 ℃时，两种热源下的磁流体域最高温度分别为280 ℃和210 ℃，磁流体域附近结构的最高温度分别为116℃和93 ℃。相较于原始方案，优化后两种热源冷却方案的改进均效果显著，相比于优化前磁流体域在两种热源下的最高温度，分别降低了173 ℃和95 ℃。对新结构进行相同的实验，并通过温度测量孔测得在700 ℃和500 ℃的热源条件下，磁流体域最高温度分别为268 ℃和196 ℃，仿真与实验的误差均在10%以内，结果较为吻合。

4.2.2 实体域温度场

结构的改进优化体现在实体域，以阻隔温度传递和带走热量为目的，实体域在两种热源条件下水管剖切面的温度场如图15 所示。

图15 改进后实体域两种热源下水管剖切面温度场Fig. 15 Improved temperature field in solid domain of the water pipe section of two heat sources

由图15 可以得知，将实体域的温度分别设置为700 ℃和500 ℃时，靠近热源区域的平均温度分别在580 ℃和390 ℃左右，水流域附近的温度分别在51℃和47 ℃左右。由于新增了冷却区域和隔热气孔，磁流体周围结构的平均温度分别为145 ℃和111 ℃，可见两种热源高温区域的温度均有所降低；相较于优化前，在两种热源条件下，实体域在靠近热源位置的平均温度分别降低了30 ℃和17 ℃，因为该区域非常靠近热源，因此温度降低的程度不大；水流域附近实体域的温度分别降低了39 ℃和32 ℃。

4.2.3 水流域温度场

因实体域的结构改进，水流域也随之变化，水流域在两种热源条件下水管剖切面的温度场如图16 所示。

图16 改进后水流域两种热源下水管剖切面温度场Fig. 16 Improved temperature field of water fluid domain in the water pipe section of two heat sources

由图16 可以得知，将水流域的温度分别设置为700 ℃时的平均温度为42 ℃左右，在500 ℃时在平均温度为32 ℃左右，充分说明介质水能够较好地带走热量；相比于优化前，温度为700 ℃时平均温度降低了15 ℃，在500 ℃时降低了16 ℃。

4.2.4 水流域压力场

结构的改变，也会对水流域的压力产生一定的影响，水流域在两种热源条件下水管剖切面的压力场如图17 所示。

图17 改进后水流域两种热源下水管剖切面压力场Fig. 17 Improved pressure field in water fluid domain of the water pipe section of two heat sources

由图17 可知，700 ℃和500 ℃时压力场的最大值为1.114×105Pa 和1.115×105Pa，二者均为1 个大气压（未包括外界的大气压），而实际压力场为2个大气压，约2 kg 压力。由仿真结果证明，结构的改变对水流域的压力并不产生影响。

5 结论

1）优化前，两种热源温度下的磁流体附近结构的温度分别为220 ℃左右和120 ℃左右，超过了磁流体的正常工作温度，会降低磁流体的寿命，加速整个结构的损坏，因此，做出了增加冷却水道和隔热气孔的结构改进。

2）增加冷却区域和隔热气孔后，两种热源均能明显并有效降低该结构温度，水流压力和速度并无明显变化。当热源温度为700 ℃时，磁流体域的最高温度相比优化前降低了173 ℃，实体域在靠近热源区域的平均温度降低了30 ℃，水流域的平均温度降低了15 ℃；在500 ℃时，三者分别降低了95 ℃、17 ℃和16 ℃；由此证明该方案的优化效果明显。

3）在700 ℃和500 ℃两种热源温度下，磁流体域附近结构的最高温度分别为116 ℃和93 ℃，在700 ℃下，最高温度超过了100 ℃，但也仅仅只在磁流体域的一个角，并不影响整体结构的运行，因此该优化方案可以降低结构整体的温度，也可以将磁流体的温度降低至正常工作范围，提高其使用寿命。