基于生命周期成本的某水闸维修加固方案优化

李俊逸

(新疆塔里木河流域干流管理局新其满管理站，新疆 阿克苏 842200)

建国以来，为了应对水患和充分发挥有限水资源的价值和作用，各级政府投入大量的人力物力兴建水利工程设施，对农业和社会经济的发展起到了十分重要的作用。时至今日，许多建成于20世纪70年代的许多水利工程，特别是水闸仍发挥着巨大作用。但是，这些水闸在设计建设时受到当时经济技术等因素的制约，大多存在设计不合理、施工技术水平落后以及后期维护不当等问题，因此存在不同程度的病险问题[1]。由于水闸等大型水利工程一旦失事，将会造成十分严重的后果，因此有必要对这些病险水闸进行维修和加固，保证其长期安全性和稳定性[2]。

从生命周期的视角来看，组成水闸工程的各个构建均有自己的生命周期，且一般小于整体水闸的工程周期。因此，对组成水闸的构件进行必要的健康诊断，对有问题的部分进行加固乃至更换，可以有效提升水闸的整体性能，有效延长水闸的寿命和服役年限[3]。由于我国的大多数水闸已经运行了五六十年，基本步入其生命周期的“中老年”，因此健康状态呈现出不断恶化的态势不仅有较多的地方需要维修加固，且加固的次数也愈加频繁，导致工程的运行管理成本不断攀升。对于水闸工程的维修加固而言，全方位、更好的维修加固措施往往意味着更多的资金投入，水闸的整体安全水平提升效果也更显著[4]。但是，节能高效的现代经济社会对威胁计划的成本投入提出了新的、更高的要求。因此，如何保证水闸结构在全生命周期内的安全性要求，同时又体现经济层面的合理性，就成为当前水闸维修结构工程设计中亟待解决的问题。基于此，此次研究以某水闸为例，探讨基于生命周期成本的维修加固方案优化方法，以便为相关类似研究提供理论和实践方面的借鉴。

1 研究过程与方法

1.1 工程背景

此次研究以某水闸为例展开，其基本概况如下：该水闸是一座干流控制性水利工程，其闸底高程为7.5m，闸顶高程为19.5m，共有16孔，单孔净宽为4.20m，闸室的总宽度为81.24m，水闸工程的全长为173.06m，闸孔净高为4.00m，设计流量为823m3/s。闸室的底板为宽顶堰结构设计，采用消力池进行消能，其池底的高程为5.00m，水闸的闸门为平面钢闸门设计，启闭机为QP2×125kN卷扬式启闭机，备有4套浮箱式检修闸门，闸墩和胸墙为钢筋混凝土结构，混凝土标号为C30，水闸交通桥桥面高程为19.5m，净宽8.00m，为双向单车道设计。该水闸建成于20世纪70年代初，于1973年正式投入使用，截止2022年已经服役49年。该水闸由于设计建设标准相对较低，加上长期运行和维护不善，一直受到病险问题的困扰，截止2016年，已经进行了5次出现加固，基本解决了关键性的病险问题，目前处于基本安全状态。

1.2 优化方法与过程

1.2.1 维修计划优化内容

基于全生命周期的水闸维修方案优化，其内容包含维修方法优化和维修时间优化两大基本维度。

首先，水闸的维修计划优化的本质就是有效平衡维修的成本和效果[5]。显然，不同的水闸维修方法需要的成本存在一定的差异，同时在维修效果方面也有所不同。一般来说，所谓好的维修计划就是通过加倍的维修成本投入达到尽可能好的维修效果。因此，在水闸维修方案优化过程中，维修方法的选择和优化极为必要。

其次，水闸的维修时间间隔是全生命周期内维修次数的主要影响因素，而维修次数会直接影响维修的成本。显然，较短的维修时间间隔会导致维修成本的抬升，但能够使水闸性能维持在一个相对较高的水平；反之，维修时间间隔的增加有助于降低维修成本投入，但必然会降低水闸的结构性能[6]。因此，全生命周期视角下水闸维修方案优化需要协调好维修成本和维修效果，确定最佳的维修时间。从时间序列来看，水闸维修可以分为定期维修和必要性维修两种基本方式。显然，上述两种基本的维修方式均有自身的优势和不足。基于此，此次研究在全生命周期的视角小下，探求最佳的维修时间间隔，最大限度发挥资金的作用和价值。

1.2.2 维修方案优化模型

假设背景工程由n个需要考虑的构建组成，以上述优化内容为基础，确定维修加固方案优化模型。其中，模型的决策变量表达式为：

(1)

目标函数的表达式为：

(2)

模型的约束条件为：

Sn≥[S]

(3)

式中，X—模型的维修策略变量；tmn—水闸构件n进行第m次维修的时间间隔，a；kmn—水闸的构建n进行第m次维修时所采用的维修方法；Ct—水闸结构的整体维修奋勇，元；CRi—水闸的各个构建的具体维修费用，元；Sn—水闸的结构性能；[S]—水闸结构性能的最低允许值。

1.2.3 计算方法

遗传算法是一种以生物进化规律为思路借鉴的随机优化搜索方法，比较适合此次研究的需要，因此研究中利用该方法进行模型的求解计算[7]。一般来说理想的理论往往相对比较复杂，在实际操作中存在较多的困难和不确定性，因此在此次研究中一般的计算方式进行适当简化，提出如下比较可行的实施步骤：

首先，由水闸的管理部门和相关专家对水闸的现状和维修需求进行综合评估，确定出一个恰当、可行的水闸建筑物维修次数范围。这里需要说明的是资金和人员工作对维修次数的影响最为显著[8]。一般来说，如果水闸的管理单位有充足的资金支持更多次数的维修，且维修工作不会对水闸维护人员的相关工作开展产生显著负面影响，可以考虑适当增加维修次数。当然，如果资金比较缺乏，则可以考虑适当减少维修次数。对于背景工程，目前已经使用了49年，预计其生命周期还有50年，结合实际情况认为在剩余的生命周期内准备大修5～8次。

然后，将上一步确定的维修次数范围纳入模型计算的限制条件，并在其范围内考虑维修方法和成本的平衡，并利用模型计算获取不同维修次数下的具体费用。计算过程中利用MATLAB进行遗传优化算法的计算，设置种群规模为800，染色体长度为16，交叉概率为0.7，变异概率为0.3，进化次数为500。

最后，根据计算结果，对比确定成本最低的维修方案，即为最终的优化方案。

1.3 计算方案

对于水闸维修加固而言，具体的维修方法和加固措施的具体费用和可以达到的加固效果的相关研究不多，因此较难获得具体的量化值，因此在此次研究中仅能予以简单的定性处理。同时，关于水闸结构的多种维修措施的叠加效果研究也比较复杂，尚无可以借鉴的成果，因此研究中假定每次维修中各个结构也仅采用一种固定的维修措施。基于此，研究中针对背景工程的实际情况，确定5种不同的维修加固方式，其对应的加固效果和投资水平见表1。

表1 维修加固方式设计表

2 计算结果与分析

利用上节构建的模型以及提出的计算思路与方法，针对背景工程生命周期内的大修方案进行模拟计算。根据计算结果，获得大修次数分别为5、6、7、8次的最佳维修计划，结果分别见表2—5。从计算结果可以看出，不同大修次数下的最佳维修计划方案均可以满足使用年限的要求，但是各方案的全生命周期维修加固费用存在较大的差异，在修次数分别为5、6、7、8次的情况下，全生命周期的维修总费用分别为794.3万、633.0万、505.3万、517.5万元。由此可见，较少的大修次数并不能实现维修总费用的降低，反而会导致全生命周期维修费用的大幅升高。例如，大修次数为5次时，最佳维修计划的总费用为794.3万元，与维修次数为7次时的费用相比，增加约57.19%。当然，大修次数过多时全生命周期的维修费用也会升高。总体来看，对背景工程而言，当大修次数为7次时的全生命周期费用最低，其对应的维修方案为最佳维修方案。

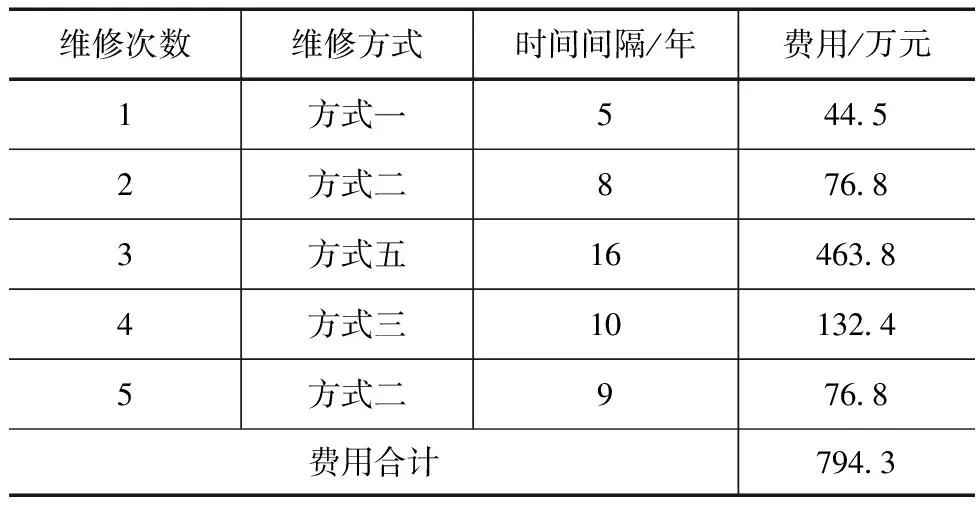
表2 大修次数5次最佳维修计划

表3 大修次数6次最佳维修计划

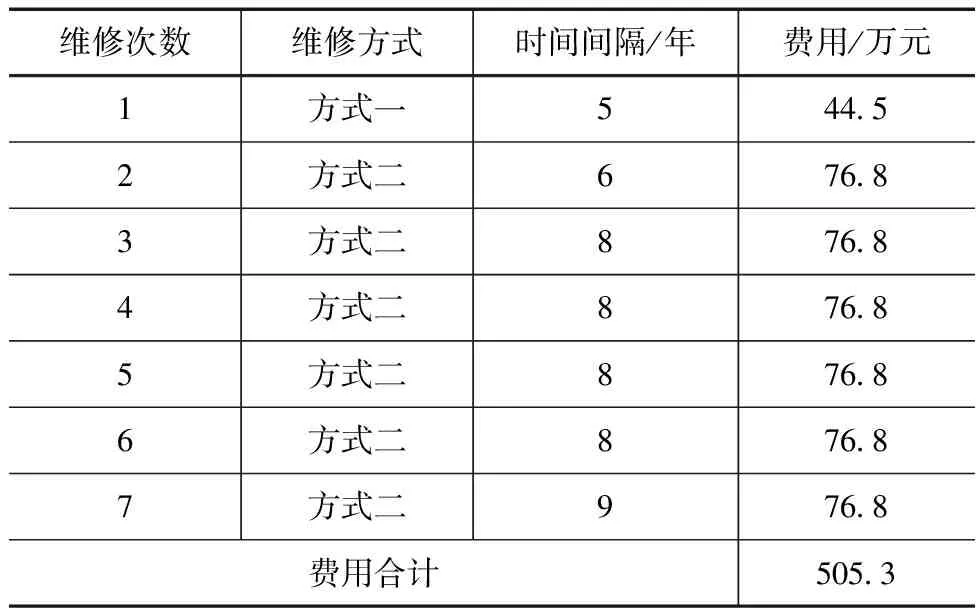
表4 大修次数7次最佳维修计划

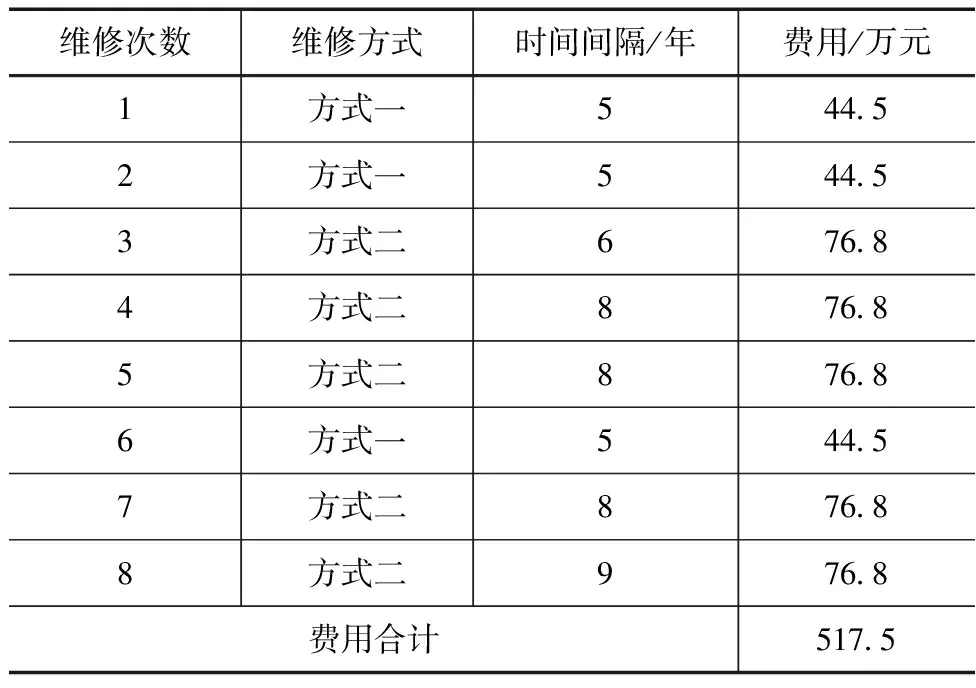
表5 大修次数8次最佳维修计划

研究中对最佳方案条件下的水闸的结构可靠度进行模拟计算。根据计算结果，绘制出结构可靠度随时间变化曲线，结果如图1所示。由计算结果可以看出，随着年限的增加，结构可靠度呈现出不断下降的变化特点，当年限为52年时的结构可靠度为0.59，已经低于0.6。由此可见，在本文提出的最佳方案条件下，可以保证水闸再安全服役52年，由于水闸本身已经服役49年，加上后续安全服役年限53年，可以完全保证该水闸最低服役100年的基本要求。

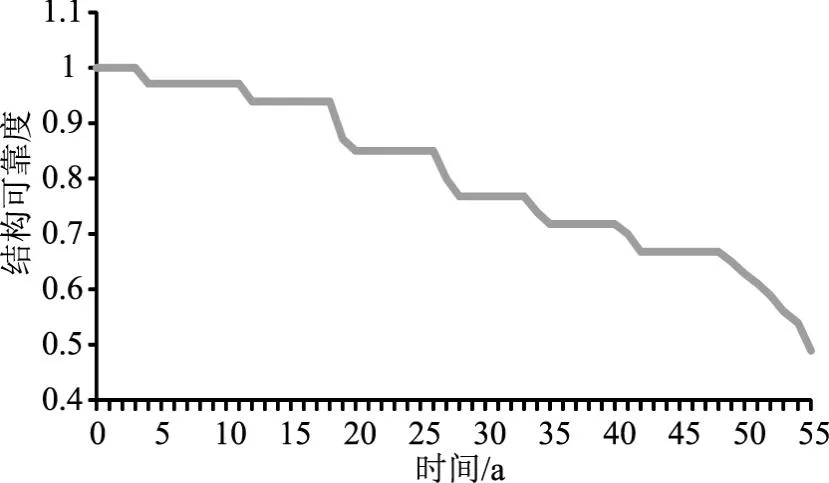
图1 最优方案结构可靠度变化曲线

3 结语

水闸的维修加固对提升其安全水平，保证其功能发挥具有重要意义和作用。在服役期限内，采用最小的维修成本获得最佳的维护效果一直是学界和工程界所关注的重点。此次研究以具体工程为背景，探讨全生命周期水闸维修加固方案的优化计算方法，并获得背景工程的最佳维修加固方案，具有重要的理论意义和应用价值。当然，维修方法的效果和成本都是最优方案的影响因素，但是目前可以用于量化研究的相关资料较少，因此研究中仅针对固定维修措施展开。在今后的研究中，需要针对不同维修方式的组合进行进一步的深入研究，以便获得更为全面的研究成果，为工程应用提供更有利的支持。