基于博弈论的水生态PPP项目风险分担研究

王 超

(北京市泽通水务建设有限公司，北京 101100)

近年来，PPP模式在我国得到了快速的发展，PPP项目日益增多[1]。但是由于相关法律法规并不完善、实践经验有所欠缺，在PPP项目操作过程中，照搬国外模式，未考虑我国国情，导致大批项目出现各种各样的问题[2-3]。同时，各地区为了响应上级政策，在没有考虑实际需要的情况下开工建设PPP项目，这些PPP项目在风险管理制度方面设计不健全，最终造成项目失败[4-6]。在这种背景下，我国PPP模式进入“冷静期”，各地区也已经加大对新PPP项目的审查[7]。

PPP项目具有合同复杂、参与方众多、合作周期长等特点，尤其是水生态PPP项目，具有一定的公益属性和公共属性，在其全生命周期的各个阶段都存在风险，可能发生风险事件。如果不能对风险进行有效的控制，可能会给水生态PPP项目带来巨大的损失，甚至直接导致项目失败。因此，对水生态PPP项目存在的风险进行科学的评估，设计合理的风险分担机制，就显得尤为必要。

1 水生态PPP项目风险评价指标体系

完善的评价指标体系是进行风险评价和风险分担的前提和基础。为了建立合理的水生态PPP项目评价指标体系，本文首先采用文献调研法对水生态PPP项目的风险进行了初步的识别；接着，采用调查问卷法和专家访谈法对指标进行删减和补充；最后，采用因子分析法对指标进行分层和归类，得出最终的风险评估指标体系。同时，本文采用因子分析法确定指标权重。

1.1 基于因子分析法的指标体系建立及权重计算

本文采用因子分析法建立水生态PPP项目风险评价体系，并建立指标权重的计算，具体步骤如下：

第一，提取数据。采用因子分析法需要大量的客观数据，即数据越多则评价结果越客观、准确。定性指标由于其主观性较强，容易给指标赋权带来影响。采用因子分析法能够解决该问题。本文将调查问卷数据收回后作为风险分析数据库。

第二，信效度分析。信度分析和效度分析是验证问卷调查是否符合标准的方法之一。在对数据进行因子分析之前必须进行信效度分析。本文采用Cronbachs alpha法进行信度检验，其公式如下：

第三，进行KMO检验和Bartlett球形检验。当KMO的数值越接近于1时，说明越适合采用因子分析。在计算KMO值时，可采用SPSS软件进行操作。Bartlett球形检验可以用来检验指标相关性，一般来说，当Sig<005时，表示满足要求，可以采用因子分析法。

第四，对公共因子进行求解。采用SPSS软件对原始数据进行分析，得出因子负荷矩阵，当累计方差贡献率大于75%的时候，将其作为公共因子，即二级指标。同时，对因子负荷矩阵进行旋转，可得：

X1=b11F′+b12F′+…+b1mF′+γ1

X2=b21F′+b22F′+…+b2mF′+γ2

…

Xp=bp1F′+bp2F′+…+bpmF′+γp

第五，计算因子得分并确定指标权重。因子得分系数表达式为：

F1=c11X1+b12X2+…+b1pXp

F2=c21X1+c22X2+…+c1pXp

…

Fm=cm1X1+cm2X2+…+cmpXp

则因子权重计算公式为：

1.2 构建指标体系

根据上述方法，构建了水生态PPP项目风险指标评价体系，具体见表1。

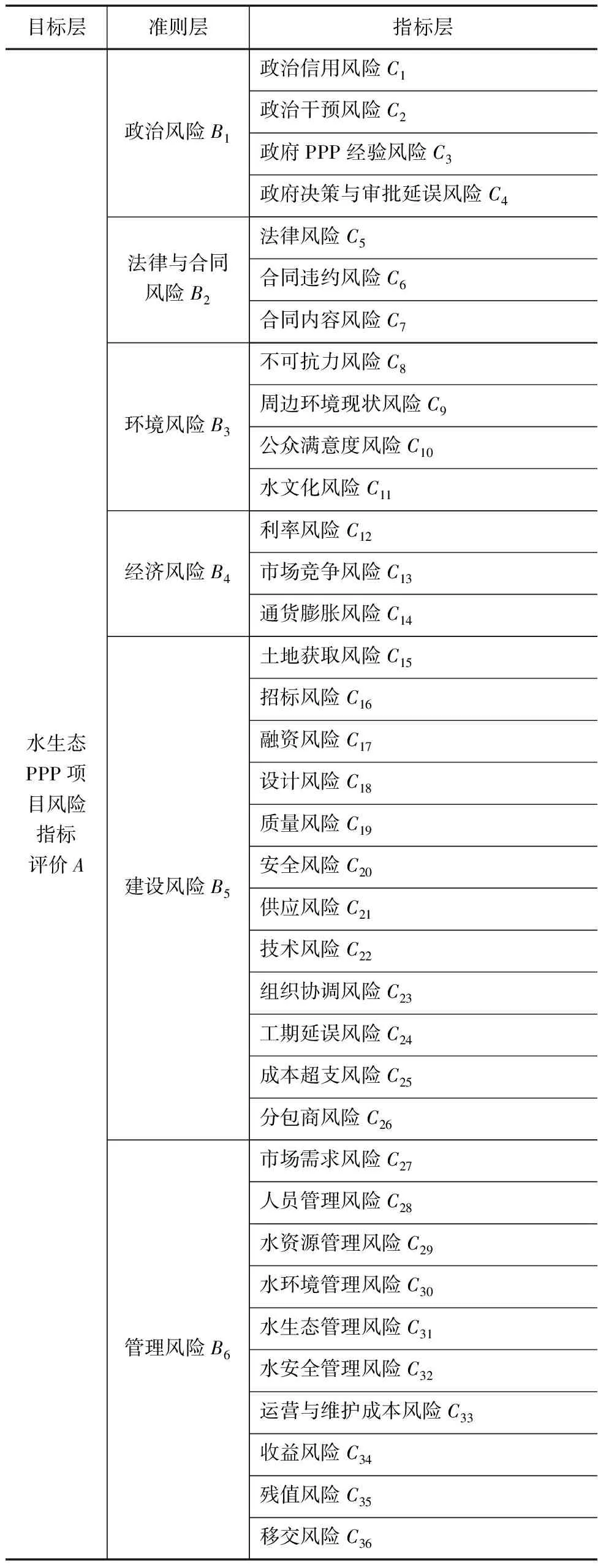
表1 水生态PPP项目风险指标评价体系

2 基于多层次模糊综合评价法的水生态PPP项目风险评价

水生态PPP项目由于其自身特点，决定了风险具有一定的模糊性。因此，本文采用模糊综合评价法对其进行评价，具体步骤如下：

第一，确定评价集及相关因素集。假设U为评价集，则有U={u1，u2，u3，…，un}，其中，u表示评价因素。将评价集设定为5个等级，则有V={低、较低、中、较高、高}。

第二，计算权重。根据层次分析思想，将指标集划分层级，并表示为U={u1，u2，u3，…，uk}，其中，u表示评价指标，将结果进行规范化处理，确定指标权重。

第三，对水生态PPP项目风险指标进行模糊综合评价，确定隶属度矩阵，并进行计算，可得：

Bi=Wi×Ri=(wi1，wi2，wi3，…，win)×

第四，进行综合评价，计算公式如下：

B=W×(B1，B2，…，Bk)T

=(w1，w2，…wk)×(B1，B2，…，Bk)T

3 基于博弈论的水生态PPP项目风险分担分析

3.1 博弈分析

生态PPP项目参与方众多，包括社会资本、政府、SPV公司、施工单位等等，但是主要参与方可以分为政府方和社会资本[8-9]。因此，本文将上述两方作为风险分担的主要对象来展开讨论。

一般来说，影响水生态PPP项目的风险承担因素主要包括对风险的偏好程度、预期净收益以及投入成本。其中，风险净收益计算公式为：

在本次博弈中，涉及到的模型要素见表2。

表2 模型要素集相关假设

3.2 模型的构建

政府的目的是公众满意，社会资本方的首要目的是自身利益。因此，要在双方博弈中找到平衡点，达到双方能够接受的状态。承担风险一方的总净收益为：

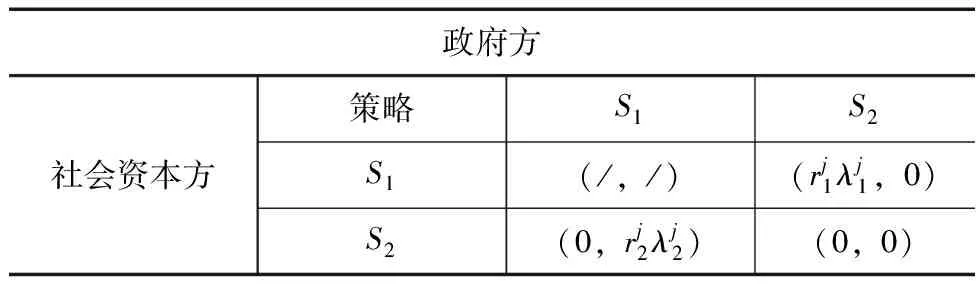
表3 政府与社会资本方博弈模型

对风险进行分配时，双方应当对风险因素比较了解，在此基础上进行讨价还价。因此，本文基于完全信息条件下的政企双方对风险分担进行博弈分析。

假设政企双方共同承担的风险为π，政府方提出不承担的风险部分为k，社会资本方不承担风险部分为1-k，双方对此分配可以接受，也可以不接受。当接受时，博弈结束。当不接受时，提出新的分配方案，直到博弈完成。在博弈之前，提出以下基本假设：

第一，政企双方愿意合作；

第二，项目风险因素之间互相独立；

第三，政府方提出不承担风险部分为k，社会资本方不承担风险部分为1-k；

第四，由政府方先出价。

在博弈过程中，假设耗损系数为δ，政府希望转移的风险部分为p。根据上述条件建立完全信息条件下的政企双方风险博弈模型：

第一轮博弈，政府提出其不承担风险部分为k1，社会资本方不承担风险部分为1-k1，由于在水生态PPP项目中，政府处于优势地位，其希望转移风险部分为p1，则本轮博弈结果为：

政府方P1=k1+p1

社会资本方Q1=1-k1-p1

如果社会资本方接受，则博弈结束。如果社会资本方不接受，则由社会资本方出价，进入下一轮博弈。

第二轮博弈，假设社会资本方提出其与政府方承担风险部分分别为k2和1-k2，社会资本方能够接受政府方风险转移部分为p2，则第二轮博弈结果为：

政府方P2=δ1(k2+p2)

社会资本方Q2=δ2(1-k2-p2)

同理，如果社会资本方接受，则博弈结束。如果社会资本方不接受，则由社会资本方出价，进入第三轮博弈。

第三轮博弈，在该轮博弈过程中，社会资本提出承担风险部分为k3，政府承担风险部分为1-k3，社会资本方能够接受政府方风险转移部分为p3，则第三轮博弈结果为：

政府方P3=δ12(k3+p3)

社会资本方Q3=δ22(1-k3-p3)

如果双方接受结果，则博弈结束。反之，则博弈继续，直至找到最优点，即双方都满意的风险分配方式。

3.3 模型的求解

为了求解，本文将第三轮谈判作为博弈模型逆推起点。在实际的博弈过程中，当政府方提出的承担风险部分与社会资本方提出的政府方应当承担风险部分相等时，才能达到最优，即p2=p3，此时可得：

k2=δ2(1-δ1k3-δ1p3)

在第二轮博弈中，当Q1=Q2时，可得到博弈均衡，此时可得：

k1=1-δ21-δ1k3-δ1p3-p1

在无限回合的博弈中，当政企双方都接受博弈结果时，即达到纳什均衡时，可得：

政府方

P分担=Q′=p1+δ2-δ1δ2-δ1δ2p3/(1-δ1δ2)

社会资本方

Q分担=P′=(1-δ2+δ1δ2δ3-p1)/(1-δ1δ2)

4 基于博弈论的水生态PPP项目风险分担理论应用

4.1 工程概况

新凤河位于北京大兴区北部，其主要功能为防洪排水和风景观赏，是北京市南部地区的重要生态廊道。20世纪80年代，随着经济的快速发展和城市的快速扩张，粗放型的生产方式使新凤河饱受生活污水、工业和养殖废水、生活垃圾等污染。新凤河流域无天然水源补充，区域再生水利用率低，河流水动力不足，人类活动密集区域河段干涸，水体自净能力丧失，生态系统脆弱。2017年3月区水务局依据“两评一案”批复结果通过政府采购方式中的竞争性磋商形式，确认北控水务(中国)投资有限公司为本项目成交供应商。采用PPP模式对新凤河进行治理。

4.2 风险评估

根据上文建立的风险指标评价体系，运用模糊综合评价法对其进行评价，得出结果见表4。

表4 新凤河水生态PPP项目风险评价等级

根据计算，得出评价结果为(0.115，0.231，0.351，0.241，0.061)。该水生态PPP项目风险等级为中级，需要制定相关的措施应对风险，加强风险监控措施。

4.3 风险分担

采用上文建立的博弈模型求解进行计算，得出该水生态PPP项目风险分配结果，见表5。

表5 政企双方风险分担结果

从表5可知，由政府分担的风险包括政治信用风险、政治干预风险、政府PPP经验风险、决策与审批延误风险、法律风险、周边环境风险、公众满意度风险、水文化风险、利率风险、通货膨胀风险、土地获取风险；社会资本方承担的风险包括融资风险、设计风险、质量风险、安全风险、供应风险、技术风险、组织协调风险、分包商风险、人员管理风险、水资源管理风险、水环境管理风险、水生态管理风险、水安全管理风险、运维成本风险、收益风险、残值风险；其余风险则有双方共担风险。

5 结论及建议

为了使评价指标体系更加科学，风险评价更加客观，风险分担更加合理，本文将因子分析法、模糊综合评价法和博弈论思想应用到水生态PPP项目的风险管理过程中，给水生态PPP项目的风险管理工作提供了新的方法。结果表明基于博弈论的风险分担模型能够对水生态PPP项目风险进行合理的分配，具有一定的推广应用价值，为当前PPP项目的发展困境提供了新的解决思路，极大地促进了PPP模式在水生态领域可持续发展。本文的博弈过程是基于双方信息完全对等情况下进行的，未讨论不完善信息条件下双方的博弈过程。因此，下一步将重点分析信息不对等条件下水生态PPP项目政企双方的博弈过程，为水生态PPP项目风险分担提供全面的理论支持。