灰色模型在蓄水池变形预测中的应用
魏周会,唐永鹏
(1.甘肃省水务投资有限责任公司,甘肃 兰州 730000;2.甘肃水务节水科技发展有限责任公司,甘肃 兰州 730000)
蓄水池工程是国家一项重要的水资源调控和灾害防控的基础设施,蓄水池的变形监测和预测对于其安全运行和维护至关重要。变形监测作为评估各类建筑物安全状况及其结构稳定性的一种必要手段,贯穿建筑物施工、竣工以及整个运营管理期内。随着数学建模和预测方法的不断发展,灰色模型作为一种简单而高效的时间序列分析方法,在各类构筑物的变形预测中得到了广泛的应用。本文将探讨灰色模型在蓄水池变形预测中的应用,以及其在该领域取得的研究进展。为蓄水池的安全管理者提供重要的数据支持[1-3]。
变形分析是对建筑物、桥梁、隧道、坝体等工程结构的变形情况进行测量、记录和分析的一种技术手段,旨在评估其结构安全性。变形预报则是根据变形监测数据,对工程结构未来的变形趋势和程度进行推测和预测的一种技术手段[4-5]。灰色模型是一种基于灰色系统理论的建模方法,通过建立灰色微分方程来描述和预测数据的变化趋势。可以处理不完备、不全面的监测数据,可以高效地在短时间内准确估计工程结构变形趋势并预测未来的变化,大大降低了工程变形预测难度;同时可以对监测数据进行插值和恢复,从异常数值中恢复有用信息,提高数据利用率。灰色模型结构简单且易于建立和使用,提高了工程变形预测的效率;具有动态调整能力,根据监测数据的实时变化不断优化预测精度,提高了变形预测结果的准确性和稳定性[6-7]。在蓄水池变形预测中,灰色模型可以根据历史变形数据建立模型,并据此预测未来的变形趋势和变形量。灰色系统模型作为一种常用的变形预测方法,在实际工程中广泛应用。通过变形预报,可以提前预知工程结构的变形情况,并采取措施进行修复和加固,避免事故的发生,从而提高工程结构的安全性和稳定性,保障人民群众的生命财产安全。在工程变形预测领域,灰色模型的应用已经取得了一些重要的研究进展。研究者们通过选择适当的灰色模型、进行数据预处理、优化模型、模型的精度评估等方面的研究,不断提高了模型的预测准确性和稳定性[8-12],并为工程管理和决策提供了重要的参考依据。需要指出的是,灰色模型在蓄水池变形预测中的应用还存在一些挑战和局限性[13-16]。例如,对于复杂和非线性的变形情况,灰色模型可能效果不佳,需要结合其他模型和方法进行综合分析和预测。此外,数据观测质量和采集频率等因素也会影响灰色模型的预测效果[16-18]。
本文利用灰色理论构建了蓄水池GNSS监测点位移的预测模型,采用MATLAB实现了相关算法;结合蓄水池的实测数据,对变形预测结果进行精度分析;并对蓄水池结构的安全性做出整体评价,为蓄水池的安全管理和维护提供更有效的支持。
1 研究方法
灰色系统理论可以深入理解研究对象的动态演化规律及其发展趋势,将研究对象抽象为输入与输出之间的关系,并基于系统动态发展的基本规律,提出了一系列新的建模思想和方法。它不仅可以进行系统分析和预测,还可以进行决策分析和优化。相比于传统方法,灰色系统理论采取一种灰度化的方式对数据的序列进行处理,能够更好地体现出数据序列的内在规律和稳定特征,更注重处理未知信息和数据的过程,从而实现对系统动态行为和发展趋势的深入分析和理解;能够通过建立合适的数学模型和算法来预测和分析未来的发展趋势、动态变化和特征规律。此外,它还具有强大的可解释性和可视化能力,能够直观地呈现分析结果和决策建议,为决策者提供科学参考和有效技术支持。灰色系统理论具有计算简单、模型高效和预测精度较高的特点;可以提供了一种直观易懂、可解释性强的建模方法。
1.1 灰色模型的建立
构建用以预测、分析和控制复杂系统的运行规律和发展趋势的数学模型,主要包含两个方面:模型建立和模型参数的估计[20]。
1.1.1 模型的建立
GM(1,1)一种基于灰色系统理论的预测方法构建的灰色模型,其适用于数据集较小、含有复杂或未知规律情形的预测,可提供更加精准和可靠的预测结果。构建的GM(1,1)模型建立步骤如下。
假设已知一组数据的序列x(1),x(2),…,x(n),我们要通过建立一个灰色预测模型来预测其后续的位移趋势。灰色预测模型的一般形式为:

我们可以将原始序列进行一次累加,得到新的序列z(i):
对新序列进行一阶差分,得到一个新的序列y(i):
y(i)=z(i+1)-z(i),(i=1,2,…,n-1)
我们将y(i)序列看作是一个一阶线性常微分方程的解,并用灰色系统理论的思想对其进行建模,得到一个灰色预测模型。其中,最常用的是灰色预测模型GM(1,1),其形式为:
式中,a、b—模型的参数,需要通过数据拟合来确定[27]。
1.1.2 模型参数a和b的估计
通过最小二乘法或最小残差平方和法,拟合出一阶常微分方程的参数a和b;
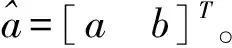
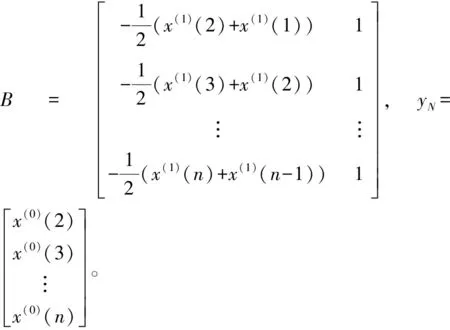
利用拟合出的参数,GM(1,1)模型的预测公式为:
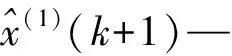
1.2 模型精度评估
灰色模型构建后,其预测精度能否满足工程需要,有必要对其进行精度检验。
由灰色预测模型可得到:
计算残差e(k)的序列

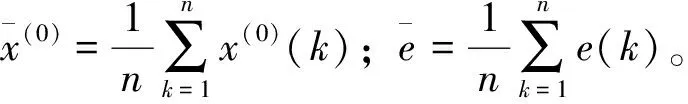
分别计算后验差比值C和小误差概率P:
C=S2/S1
用后验差比值C和小误差概率P判定模型的模型预测精度,精度检验等级见表1。

表1 GM(1,1)模型精度等级
一般来说,C值越小,表明预测的离散度小,模型的预测精度越高;P值越大,表明小误差概率大,模型的预测精度越高。
2 数据处理与分析
2.1 实验区域概况及数据准备
本次实验采用古浪县黄花滩蓄水池的GNSS监测数据,该蓄水池共布置的8个GNSS监测点进行连续观测。为得到监测点高精度的时间序列,采用GAMIT/GLOBK软件对GNSS数据进行处理。主要的数据处理流程如下:①GNSS数据预处理;②GNSS单日观测数据处理;③平差计算。具体流程如图1所示。

图1 GNSS数据处理流程图
基线解算主要的参数设置见表2,其余参数采用GAMIT软件默认设置。
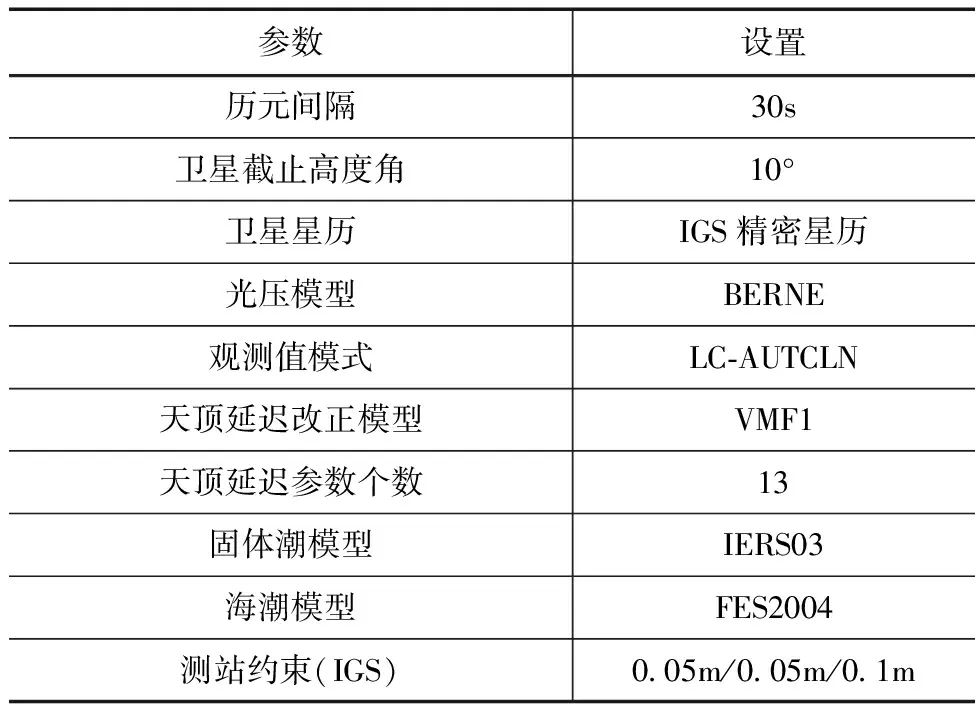
表2 基线解算参数设置
平差计算采用GSCORS基准站的坐标,平差参数设置见表3,其余参数采用GLOBK软件默认设置。
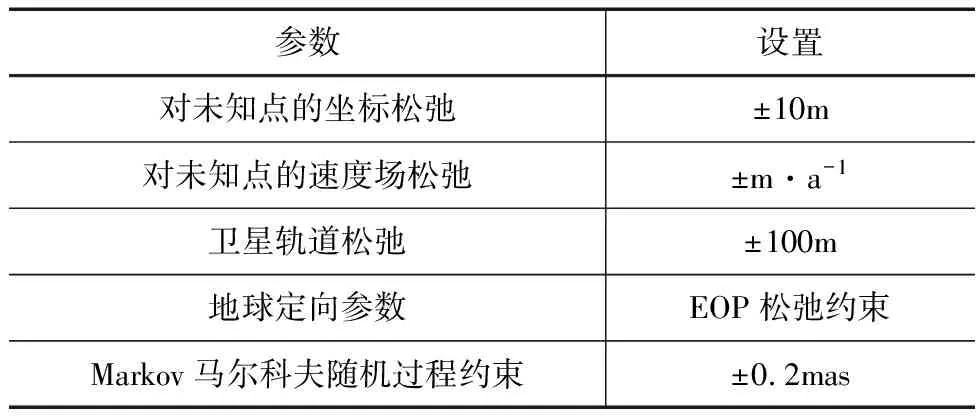
表3 平差参数设置
2.2 结果分析
对古浪县黄花滩蓄水池监测点的时间序列,采用GM(1,1)模型对实测的数据进行预测。通过用Matlab软件编写程序,用该模型做预测,得出结果如图2—4所示。
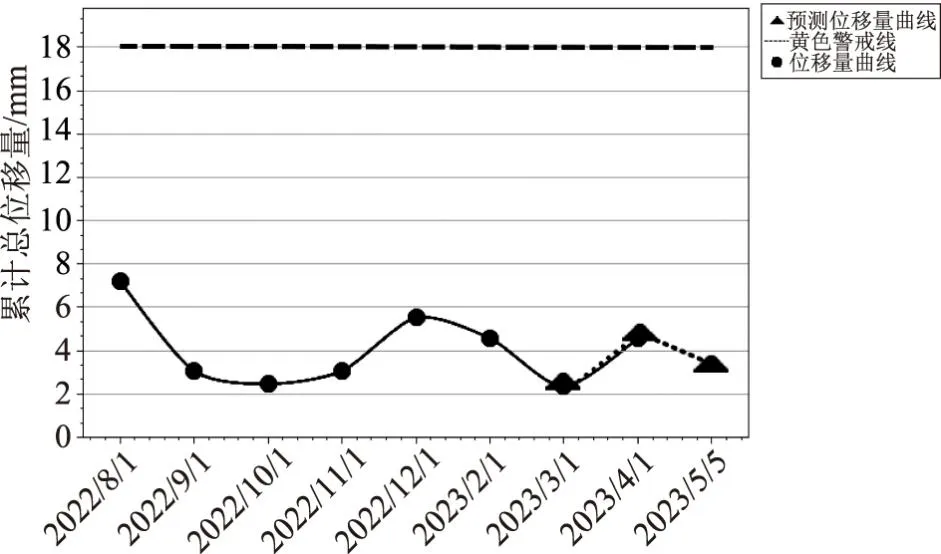
图2 2#监测点x方向变形监测位移量预测图
图2—3分别为2#监测点x方向和y方向上变形监测位移量预测图,黑色的曲线为蓄水池实际的位移曲线,由蓄水池变形监测位移量曲线图可知,监测期间累计位移量均低于警戒数值18mm,表明蓄水池运行安全。黑色的虚曲线为监测点变形监测位移量预测,在4月1日的预测值与实测数据高度吻合,验证了模型的精确程度,能反映GNSS监测点的位移变化趋势。
图3分别为2号垂直方向上变形监测位移量预测图,黑色的曲线为蓄水池实际的位移曲线,由蓄水池变形监测位移量曲线图可知,表明蓄水池运行安全。黑色的虚曲线为监测点变形监测位移量预测,在增加蓄水量后垂直方向上的沉降量增加,同样在4月1日的预测值与实测数据高度吻合,验证了模型的精确程度,能反映GNSS监测点的位移变化趋势。

图3 2#监测点y方向变形监测位移量预测图
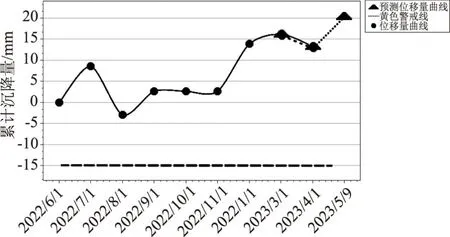
图4 2#监测点垂直方向变形监测位移量预测图
通过对每个监测点运行模型后计算得出的数据进行完整整理,可得到模型精度评估表,见表4。
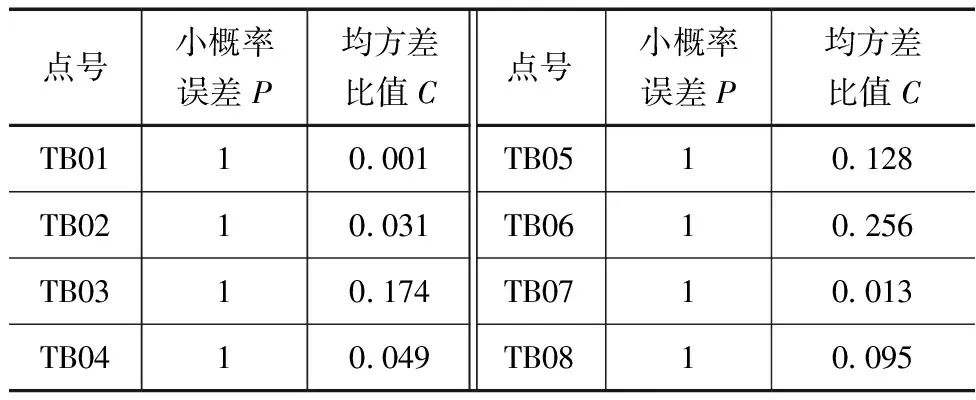
表4 模型精度评定
根据上述数据分析结果,可以得到每个点号对应的小概率误差和均方差比值。对于所有监测点,模型的精度达到了最高等级“好”,证明其精度符合要求。均方差比值用于比较预测误差大小和波动程度,数值越小说明预测越准确。由数据可以看出,TB01具有最小的均方差比值为0.001,表明该点号的预测误差和波动都非常小,因此预测效果是最准确的。相反,相对较大的均方差比值例如TB03和TB06则表明预测误差和波动都相对较大。可以看出,均方差比值C的大小与其代表的误差大小成反比,因此数值越小代表预测误差越小。从结果可以看出,模型在不同点号下的均方差比值C均在0.001到0.256之间。从均方差比值的角度来看,TB01的预测效果最好,而TB03和TB06的预测效果相对较差。但需要注意的是,这些结果都是在满足高精度要求的前提下得出的。综合来看,该预测模型的预测精度结果相对较高,并且各点号下误差比较稳定,具有一定的可信度。
3 结语
本文介绍了灰色模型的基本原理、建模方法,然后对的黄花滩蓄水池的监测点GNSS数据进行处理,获得了高精度的时间序列,而后通过Matlab编写程序,采用灰色模型构建了黄花滩蓄水池的监测点的预测模型,并结合实测数据进行了比对分析。主要的结论如下:
(1)基于灰色模型构建的监测点预测模型,具有很高的精度。模型预测的结果逼近实际测量结果,模型具有可行性和有效性,适用于蓄水池变形监测的应用要求。
(2)用后验差比值C和小误差概率P判定模型预测精度,蓄水池所有监测点精度均达到了模型精度等级最高等级“好”,证明其精度能够满足蓄水池变形监测要求。

