基于FPGA的硅微陀螺数字测控和温补技术研究
胡 远,黄海滨,陈东傲,徐大诚
(苏州大学 电子信息学院,江苏 苏州 215100)
0 引言
硅微陀螺由结构和测控电路两部分组成,测控电路集成化也是近年来的发展趋势。目前国内外研究机构的测控电路大多为模拟接口电路完成信号读出,FPGA实现陀螺仪信号处理和控制,采用分立器件实现的方案。国外Bosch公司[1]、STM公司[2]、佐治亚理工学院[3]等,国内北京大学[4]、东南大学[5]、上海微系统所[6]等都对陀螺仪测控ASIC展开研究。除了信号读出部分,信号处理和控制部分也多采用模拟ASIC完成,缺乏数字化输出[7]或最终采用高精度ADC实现[8],存在体积大功耗高的问题。相比模拟电路,数字电路抗干扰能力更强,更善于信号处理和数字化输出,所以有必要进行陀螺仪数字ASIC研究[9-11]。在陀螺仪数字测控电路的研究过程中通常采用先Simulink模型仿真,然后用IP或工具生成代码集成整个系统验证性能的方案,不利于数字测控ASIC实现。在分析硅微陀螺结构和工作原理的基础上,通过硬件描述语言实现测控功能是一种有效实现陀螺仪数字ASIC途径。
针对以上问题,本文采用Verilog硬件描述语言设计陀螺仪数字测控系统,驱动模块采用自动增益控制(AGC)和锁相环(PLL),敏感模块采用科氏力平衡闭环和正交校正闭环,考虑温度对陀螺性能的影响,利用驱动轴谐振频率和温度的关系[12],对标度因数和零偏进行补偿。
1 硅微轴对称陀螺
1.1 动力学方程及分析
硅微机械陀螺仪可以等效为二阶质量-弹簧-阻尼系。由于敏感模态采用力平衡闭环检测的方式,忽略敏感轴对驱动轴的耦合干扰,在理想情况下,不存在刚度和阻尼不对称,理想动力学方程可以表示为:
(1)
mx和my分别为驱动模态和检测模态的有效质量,dx和dy为阻尼系数,kx和ky为刚度系数,x和y分别为两个模态的振动位移,Fx和Fy分别为两个模态的激励信号。设定驱动模态激励信号为:
Fx=Adcos(ωdt)
(2)
Ad为激励信号幅度,ωd为激励信号频率,代入式(1)求得驱动模态位移的稳态解为:
x(t)=Axcos(ωdt+φx)
(3)
Ax为振动位移幅度,φx为驱动模态相移,敏感模态传递函数同驱动模态一致。则位移稳态解为:
y(t)=Aycos(ωdt+φy)
(4)
(5)
(6)
Ay为振动位移幅度,φy为敏感模态相移,ωx为驱动轴频率,ωy为敏感轴频率,Qx为驱动模态谐振频率,Qy为敏感模态频率,从式(5)可以看出,力平衡模式下通过检测敏感振动幅度大小可以计算出输入角速率。
在实际加工中,由于工艺问题会造成陀螺刚度和阻尼的分布不均匀,与电极轴有偏角,在硅微陀螺二阶动力学方程中会有刚度和阻尼的耦合误差项。在科氏输出中会有正交误差项和同相误差项,对硅微陀螺仪的高精度测量产生性能影响,对于采用真空封装的陀螺,同相阻尼可忽略不计,正交误差影响较大。
当外界输入角速度时,敏感模态产生振动位移,经过模拟接口电路拾取信号后得到检测输出Vs,通过ADC转换后进入FPGA中。由科氏力数学公式可知,敏感模态的检测输出Vs,在忽略刚度和阻尼误差时,可以表达为:
(7)
其中:kc/v为敏感模态模拟接口电路的总增益。由于陀螺敏感模态的检测输出必须经过解调,其解调参考信号是来自驱动部分PLL的输出信号。可知信号Vs的噪声源主要有3个部分:敏感模态接口电路的噪声、驱动模态振动速度的幅度噪声和PLL输出信号的噪声。综上,一个低噪声的模拟接口电路,低噪声的PLL、高稳定性的AGC是实现陀螺高精度输出信号的前提。
根据陀螺批次不同,其有不同的谐振频率,模拟接口电路输出的有用信号频率在5~20 kHz之间,由奈奎斯特采样定理可知,采样频率至少为40 kHz。考虑所使用ADC最高采样频率,本文ADC采样频率为625 kHz,后续数字算法以此频率为时钟。对于18位的ADC其量化误差SNRQ分贝形式可表示为:
SNRQ≈6.02*b+1.76=110.12 dB
(8)
量化噪声可视作加性噪声,可以通过增加位宽和动态范围内输入信号的幅值来提高ADC信噪比。本文ADC输入参考电压Vref为2.5 V,满量程5 V,模拟接口C/V信号拾取电路的噪声经测试为230 nV/√Hz,则输入信噪比SNRin:
(9)
可以看出,选择18位的ADC足够保证其量化噪声小于模拟接口电路信号噪声。
1.2 力平衡模式测控系统
力平衡模式测控系统如图1所示,包括两个部分:接口驱动部分和数字算法部分,接口驱动部分包括DAC(数模转换器)、ADC(模数转换器)、串口等硬件的驱动;其中数字算法采用AGC和PLL驱动陀螺稳幅稳频的振动,科氏力闭环抑制敏感模态的科氏振动,正交校正闭环从结构刚度耦合层面上抑制正交误差,其基础构成算法为乘法解调算法、PI(比例积分)控制、NCO(数控振荡器),其中数字算法部分如图2所示。
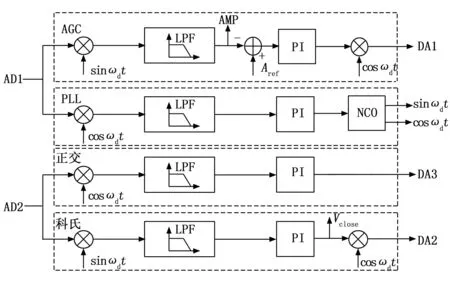
图2 力平衡模式数字测控算法
在Vivado2018环境下设计了测控系统,用自带仿真软件Simulator进行功能仿真。
FPGA设计流程为:综合将用硬件描述语言的输入转换为 FPGA 能够识别的描述,得到门级网表,与FPGA内的逻辑块和硬件资源相对应。综合之后得到门级网表,通过在 FPGA 内自动布局、布线工具将内部逻辑块连接起来,通过指定的 IO 口进行输入输出。约束包括位置约束和时序约束。位置约束是指分配顶层设计的输入输出引脚和电平与FPGA芯片相对应。时序约束是让时序收敛,保持建立时间和保持时间不违例,影响着布局布线。仿真主要包括功能仿真、综合后仿真和时序仿真。功能仿真是为了验证寄存器传输级(RTL)级描述下是否能够准确实现设计的功能,又称为行为仿真。综合后仿真是验证综合后结果是否与原设计一致,又称为门级仿真。时序仿真是加入布局布线后模块和连线之间延时的仿真,更接近实际情况。静态时序分析是为了查看各个路径延时,延时最大的路径决定了整个系统最高频率,对于不满足时序要求的设计要进行修改。在以上步骤分析和验证后,生成bit流,下载至FPGA芯片中,也可固化到配置Flash芯片中。
在FPGA平台上,浮点运算很不方便,所以信号和系数均以有符号定点数形式参与运算,定点数即小数点位置固定,在设计初约定好。如补码形式24Q21定点数表示总位宽24 bit,小数位21 bit,整数位2 bit,最高位表示符号位,格式精度为1/221,约为0.000 000 48,能表示数的范围为[-4,3.999 999 52]。以24Q21格式表示的数,需乘上221,结果保留整数位即可。对于有符号数的基本运算,reg和wire类型要用signed修饰。
PLL第一个部分是鉴相器采用的是乘法鉴相器,PI控制器构成环路滤波器,用数控振荡器替代压控振荡器。AGC环路的鉴幅器部分采用的是乘法鉴幅器,提取驱动模态振动幅值的原理与乘法鉴相器类似,通过低通滤波器滤除二倍频分量后得到幅度信息,增益为1/2。
首先在AGC和PLL中都需要乘法器和低通滤波器,乘法器的输入为驱动模态检测信号(24Q21),PLL输出的sin和cos信号(24Q21)。相乘结果经过截断处理后送入低通滤波器中。乘法作为基本运算的核心,Vivado综合器会将乘法运算符综合优化为移位相加结构,在一个时钟周期内输出计算结果。本文数字算法为625 kHz,频率较低,无需流水线结构,性能也能满足需求。低通滤波器由FIR(有限脉冲相应)和IIR(无限脉冲相应)两种形式,其中FIR滤波器有着线性相位、容易设计的优点,但相同的性能指标,FIR的阶次过高,所需资源和计算时间都更长,因此选择IIR滤波器进行设计。数字滤波器有巴特沃斯型、切比雪夫型、椭圆型等形式。在Matlab中采用不同方式设计滤波器,设计指标:通带截止频率500 Hz,通带最大衰减3 dB,阻带截止频率2 kHz,阻带最小衰减40 dB,采样频率625 kHz。根据巴特沃斯滤波器阶数公式得最小为4阶,在相同阶数下各方法设计得到巴特沃斯幅频特性在通频带是最平坦的。由于IIR滤波器有反馈结构,字长效应影响较大,而级联型易于控制有限字长带来的影响。乘法解调模块中低通滤波器采用4阶巴特沃斯IIR低通滤波器,由2个2阶IIR滤波器级联而成,如图3所示。
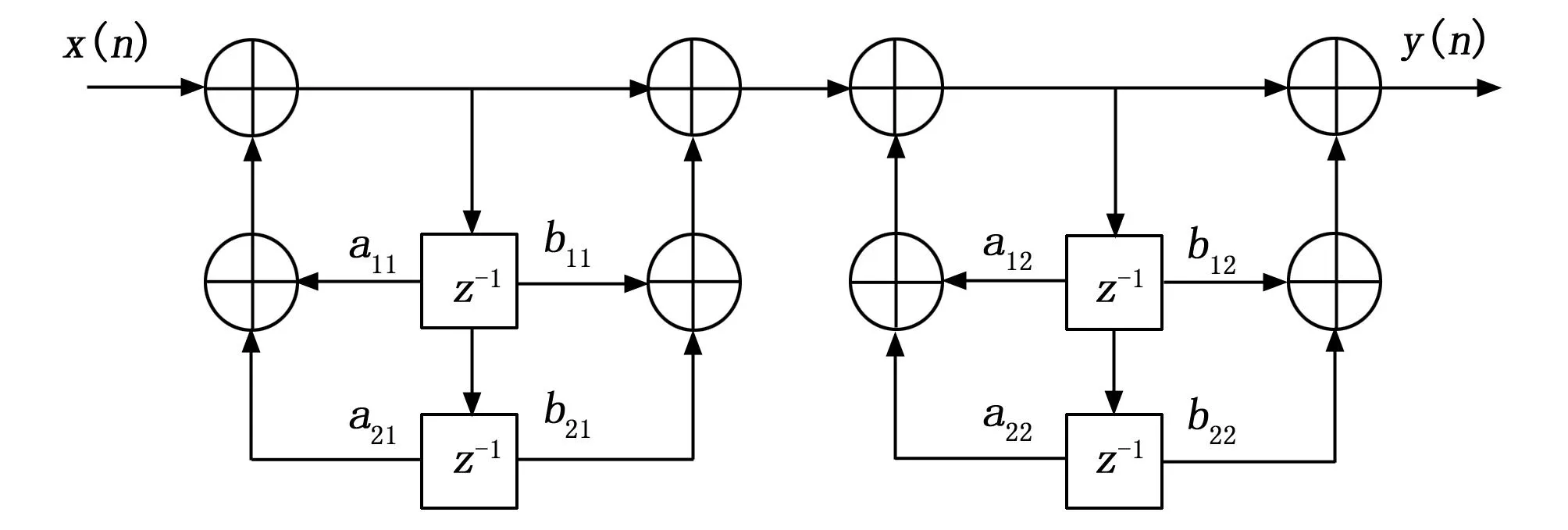
图3 级联型四阶IIR滤波器框图
仿真结果如图4所示,仿真为输入为0.001sin(ωdt)和sin(ωdt)相乘结果,ω为2π*5 000,理想滤波输出0.000 5,实际输出0.000 499 7附近,相对误差0.06%,精度满足要求。

图4 乘法解调仿真结果
AGC和PLL环路中低通滤波器的输出会送给PI控制器。带被控对象的位置式PI控制器如图5所示。PI控制器对误差信号e(n)进行比例放大和微分累加处理,负反馈闭环下误差信号e(n)会逐渐减小,使被控对象的输入信号yin和输出信号yout逐渐接近。
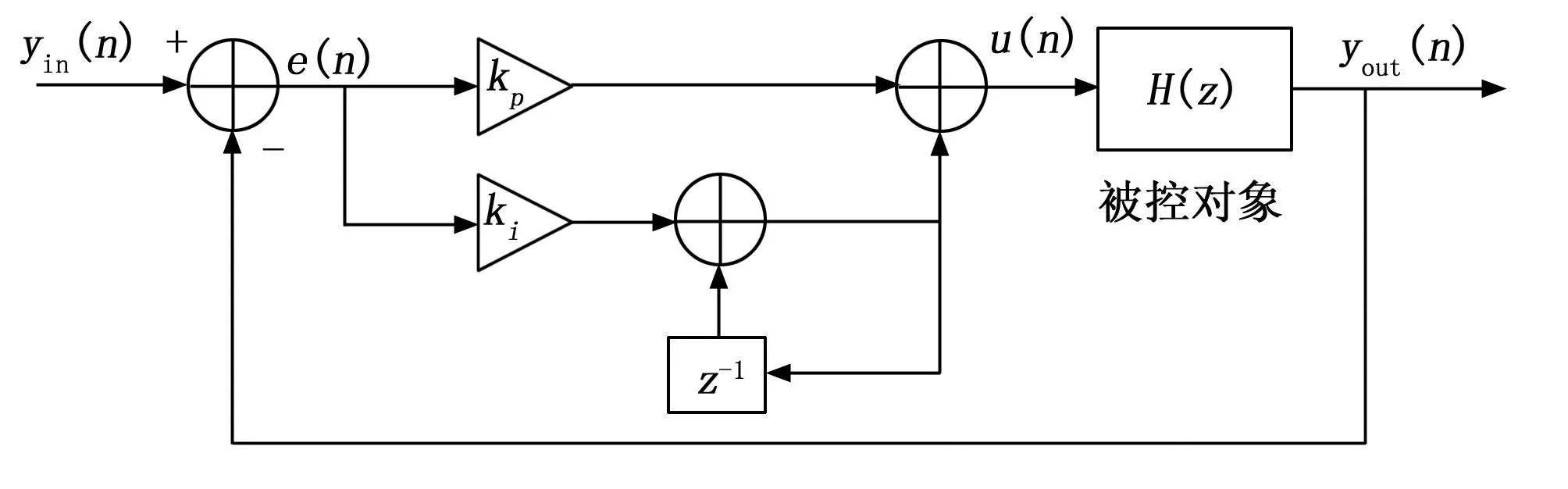
图5 带被控对象的PI控制器
比例控制能提高信号增益,有利于控制系统的快速稳定,减小稳态误差。积分控制对累计误差信号,推动PI控制器的输出不断增大,进一步减小稳态误差直至完全消除。微分控制能对误差信号的变化趋势进行预测,可以预先调整控制量,对系统误差进行有效抑制。但对于硅微陀螺仪,振幅信号的变化是缓慢的,微分控制器在这里的作用不大。而且微分控制器会放大噪声信号,降低信噪比,因此采用PI控制就可达到减小误差的目的。设定陀螺仪AGC稳幅0.5 V(24Q21),使用内嵌式逻辑分析仪ILA在线调试采集AGC稳幅输出AMP,如图6所示,理想输出为24’d1048576,实际值在其附近波动,PI控制器能稳定进行控制。

图6 ILA采集AMP结果
CORDIC算法是通过角度旋转和迭代计算逼近目标值,将三角函数运算转化为逻辑位移运算,使旋转角度无限接近目标值。NCO系统如图7所示,由输入频率控制字和相位累加器构成,CORDIC作波形发生器。频率控制字FC=(fo+ff)2M/fclk,fo为中心频率,ff为PLL中PI控制器输出信号,M为相位累加器位宽32,fclk为625 kHz。
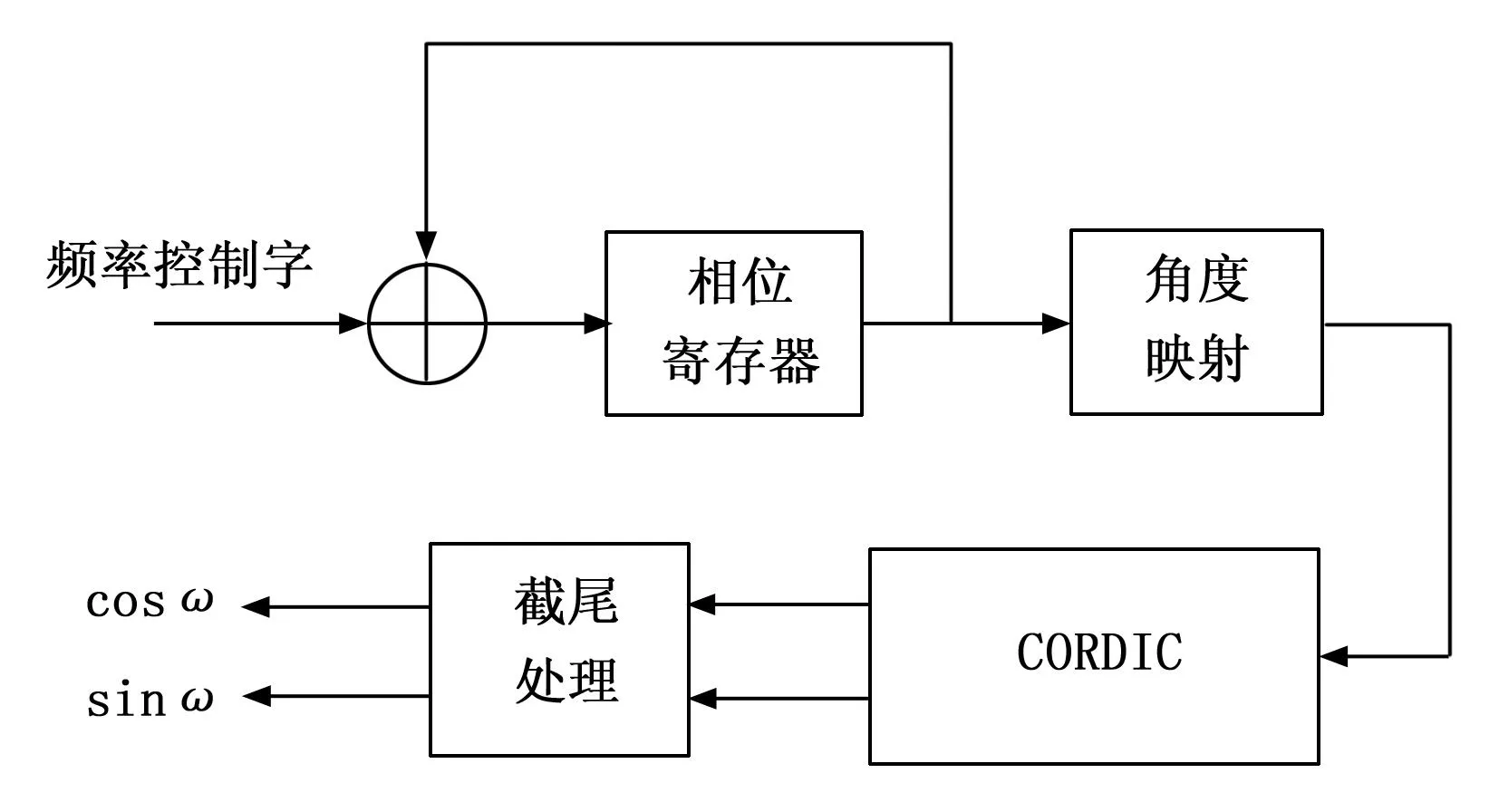
图7 基于CORDIC的NCO框图
由于CORDIC算法中角度旋转范围在(-99.88°,99.88°),因此进入CORDIC模块的信号首先通过角度映射到第一象限(0°,90°),定义2 bit的flag信号,寄存16个时钟,在最后输出时根据flag值和三角函数关系恢复对应值。CORDIC经过16次迭代,最后对输出做截尾处理产生sin和cos信号。输出信号的分辨率由相位累加器位宽M决定,频率分辨率约为0.000 15 Hz。在频率控制改变下的仿真结果如图8所示。
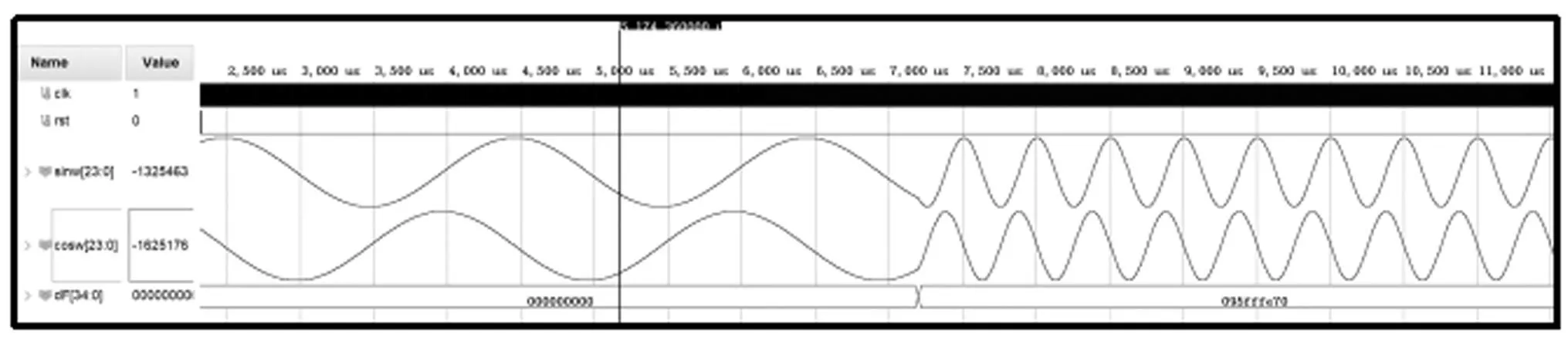
图8 NCO的仿真结果
在基于AGC和PLL的驱动方案设计完成后,驱动模态能够稳幅稳频的振动。对于敏感模态,其检测信号中包含科氏分量和正交分量,为了能够检测科氏力的大小,同时抑制正交误差,设计了科氏力闭环和正交校正闭环电路。
科氏力闭环检测有环境适应性好、标度因数和零偏稳定等优点。当外界有角速率输入时,陀螺敏感模态产生科氏力,在其作用下,敏感模态产生振动位移,通过模拟接口电路提取信息,经ADC转换进入FPGA中。其中乘法解调模块提取幅度信息,PI控制器输出经调制产生与科氏力同频反相的信号作用于敏感模态激励电极,抑制其科氏振动,所以PI控制器的输出可以反映科氏力。
受限于加工精度的限制和材料特性,硅微陀螺存在质量、刚度及阻尼不对称的问题,导致驱动模态和敏感模态不完全正交。为了抑制正交误差,常用的正交误差抑制方法有电荷注入法、正交力校正和正交耦合刚度校正[13],在这几种方案中正交耦合刚度校正方法能从结构耦合层面上消除刚度不对称,以下简称为正交校正闭环。通过乘法解调模块提取正交信号幅度,作为误差信号输入到PI控制器中。由于DAC输出电压最大幅度较小,所以将正交校正闭环中PI控制器输出信号经DAC转换后与外加电压Vqnn相加,共同施加到陀螺的正交校正电极上。采用PI控制器进行控制,正交校正闭环是一个Ⅰ型系统,当系统稳定后,稳态误差为零,正交校正闭环产生的等效刚度会与驱动模态和敏感模态之间的耦合刚度相互抵消,正交误差将会被抑制到很小。
数字算法由3部分构成:1)幅度和相位控制闭环数字部分;2)科氏力平衡闭环和正交校正闭环的数字部分;3)压控振荡器NCO模块。
在Vivado中用Verilog硬件描述语言设计AGC和PLL,输入data_x(24Q21)为经过ADC转换的驱动检测信号。DA_data1为AGC经调制后的驱动激励信号。AMP和PHA分别表示幅度和相位控制闭环中低通滤波器的输出信号(24Q21),dF为PLL环路PI控制器的输出信号。科氏力闭环和正交校正闭环的数字部分中,输入data_y(24Q21)为经过ADC转换的敏感检测信号。DA_data2和DA_data3分别为科氏力闭环和正交闭环的检测反馈信号和正交校正信号。QUA(24Q21)表示正交校正闭环中PI控制器的输出信号。内部的滤波器沿用驱动闭环系统中的设计COR代表科氏信号输出,为24位补码形式有符号数。NCO模块输入信号dF加上扫频测试中的驱动模态谐振频率,通过移位和相位累加,其结果输入到CORDIC子模块中,产生sin和cos信号,如图9所示,3个模块的信号名称端口。
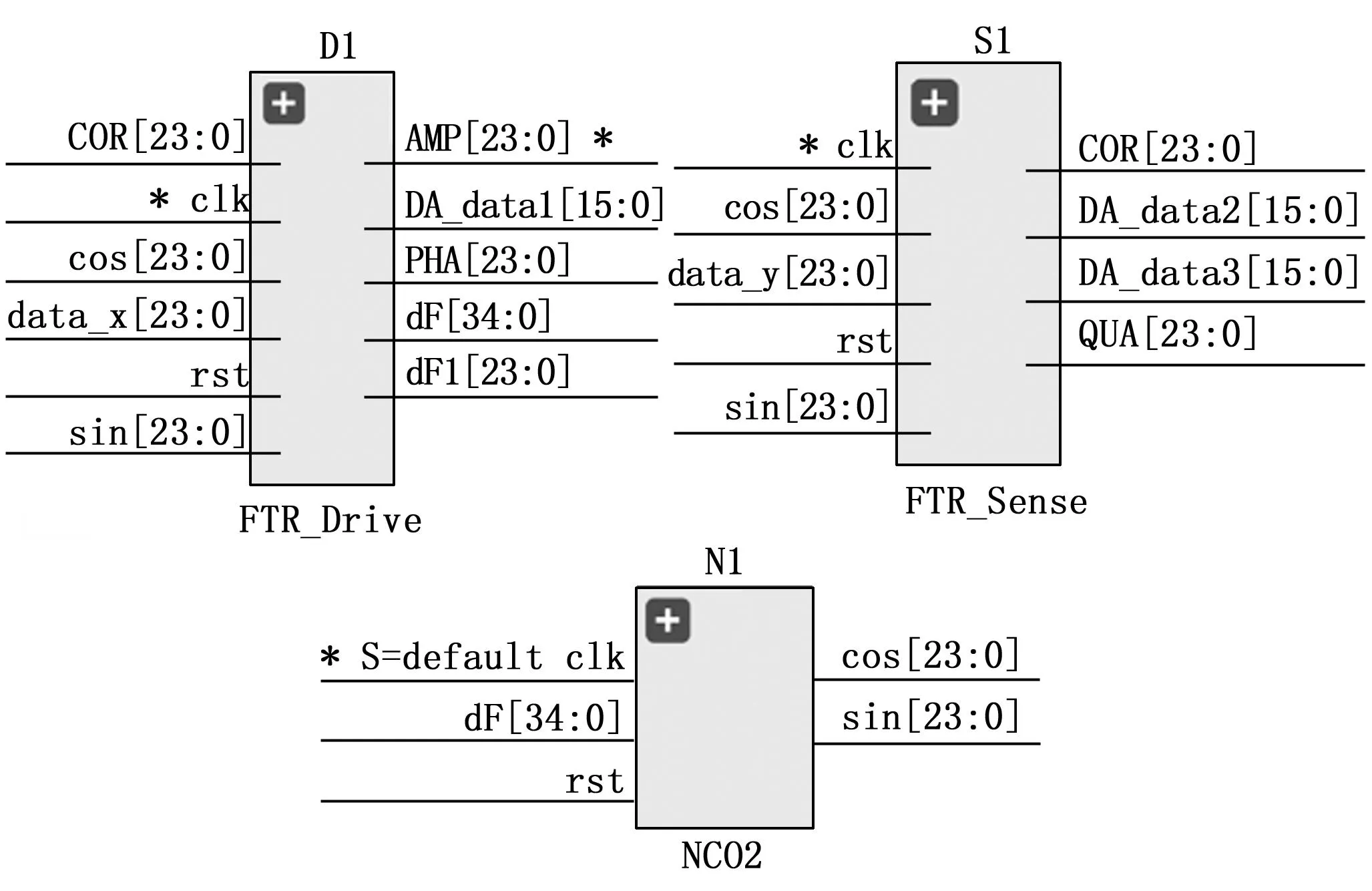
图9 主要模块和信号名称
在xc7a100tcsg324芯片上数字算法部分综合后资源消耗如表1所示。未使用到DSP48E1和BlockRAM资源,FTR_Drive和FTR_Sense模块中主要消耗资源为查找表,少量消耗寄存器。为了保证滤波精度,其中2/3的查找表都是低通滤波器中高位宽运算消耗的。NCO模块中采用并行计算的方式,模块启动经过固定时钟等待后开始输出。
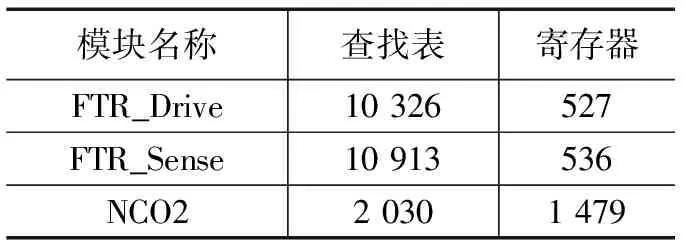
表1 FPGA资源消耗表
同FPGA一样,数字ASIC开发也要经历需求分析、设计输入、功能仿真、综合、布局布线、时序仿真及静态时序分析等步骤。不同的是数字ASIC为了验证设计的准确性会有形式验证、FPGA验证和对复杂系统的验证方法学。为了在布局布线中避免阻塞,FPGA资源利用率最好只用到70%~80%,而ASIC能更好地满足定制化需求,减小面积和功耗。FPGA是快速实现系统功能的平台,在功能实现的情况下大多不会考虑面积和功耗,而数字ASIC流片成本高,面积和功耗是必须关注的指标。
2 温度特性
当温度变化时,硅微陀螺仪的机械结构尺寸和材料的弹性模量会发生变化。材料弹性模量是物质的一种固有属性,它的变化会改变微结构的刚度,导致硅微陀螺仪的谐振频率产生漂移[14]。温度为T时的硅材料弹性模量E(T)可表示为:
E(T)=E0[1-KET(T-T0)]
(10)
式中,E0表示硅材料在温度为T0时的弹性模量,T0=300 K,KET为硅材料弹性模量的温度系数,其值在10-5数量级。由于硅微结构系统刚度与弹性模量呈线性关系,可得刚度K与温度T的关系:
K(T)=E0[1-KET(T-T0)]
(11)
式中,K0表示温度为T0时的系统刚度。硅微轴对称陀螺谐振频率与温度的关系可表示为:
(12)
式中,ωn(T)表示温度为T时的陀螺谐振频率;m为检测质量块的质量。根据泰勒公式,将上式在T=T0处展开为:
(13)
取前两项,可表示为:
(14)
由此可见,温度和谐振频率之间近似线性关系,所以采用驱动谐振频率进行温度补偿,补偿方案如图10所示。

图10 温度补偿模块
图10中,用驱动轴谐振频率计算温度,再通过温度和标度因数、零偏的关系得到SF(f)、ZROBP(f),SFref表示参考标度因数,Vclose表示科氏输出,Vcomp表示补偿后输出。
温度引起陀螺敏感单元弹性模量改变,导致谐振频率变化,同时温度影响模拟接口电路的相位,导致正交环路和科氏环路的耦合,恶化陀螺性能。所以为了提升陀螺仪的温度性能,采用驱动轴谐振频率为温度相关量,建立温度和驱动轴谐振频率的关系。
硅微陀螺仪零偏输出主要由耦合的正交误差和同相阻尼误差构成,对于采用真空封装的高Q值陀螺,同相阻尼误差可忽略不计,因此正交误差是影响陀螺仪零偏的关键因素,设计的正交校正闭环会大幅度降低耦合影响[15]。
温度影响陀螺的结构参数和电路参数,而且主要影响模拟电路。模拟电路中的滤波器、放大器、ADC、 DAC以及电子元器件都会受到温度影响产生幅度噪声,而对基于FPGA的数字测控电路,温度对其影响较小。但除了正交误差,陀螺零偏还会受到电馈通噪声、结构热噪声等因素影响,是多因素综合作用的结果。因此采用温度建模补偿的方法,该方法简单有效,不会对陀螺闭环控制电路产生额外的影响。这种采用陀螺内部变量表征温度的方法能及时反映陀螺内部温度的变化[16-17]。
BP(Back Propagation)神经网络是人工神经网络中一种经典的算法,能够学习并记忆给定的输入与输出之间的关系,具有较好的函数拟合能力。采用traingd函数作为训练函数,tanh函数作为层与层之间的传递函数,LM算法更新BP神经网络权值和阈值。采用Matlab的nntool神经网络工具箱进行数据进行建模训练,会对训练数据预处理,进行归一化和反归一化加速模型收敛[18-20]。
补偿步骤如下:
1)在0~65 ℃内驱动轴谐振频率和零偏输出。
2)将训练数据输入到BP神经网络训练模型中,通过多次迭代获得各网络层的最佳权值和阈值参数。
3)将训练好的模型参数写入FPGA中的BP神经网络中,实时补偿陀螺零偏。
BP神经网络由乘法、加法和激活函数组成,所用激活函数tanh含有指数运算,无法直接在FPGA中实现。tanh函数的数学公式为:
(15)
考虑到计算精度、实现性与资源占用问题,本文采用了分段线性插值法近似计算,如图11所示。

图11 tanh函数硬件实现方法
首先tanh(-x)=-tanh(x),只需实现x轴的正半部分,利用输入最高位判断正负选择相应的输入和输出。通过输入x移位后取高12位作为ROM的地址,地址中存放的是[0,4]等分4 096段后每一段的斜率b和偏置a,经过一个时钟的数据读取进行相乘相加。最后根据最高位判断输出。
3 测试结果与分析
3.1 测试平台与系统
以硅微轴对称类蛛网式圆盘谐振陀螺(CDRG)为实验对象是由环式结构发展而来的十六边形类蛛网型。用8个交替辐条将10个十六边形类蛛网同心环和单个中心锚点相连。在环与环之间的空隙,悬挂集中质量块和设置电极,用16个矩形梁连接环与环[21-22]。
在室温环境下使用锁相放大器HF2LI扫频采集陀螺两个模态的频率响应曲线,得到驱动轴谐振频率5 047.99 Hz,Q值为13.83万,敏感轴谐振频率5 045.56 Hz,Q值为13.75万,初始频差为2.43 Hz。通过施加10.61 V 与 8.90 V 的调轴与调频电压对陀螺,减小频率裂解,提高模态匹配程度。经过开环扫频得到频率裂解由 2.43 Hz 减小到 0.40 Hz FPGA芯片为Xilinx的xc7a100tcsg324-2,工业级温度可在-40~85 ℃。由温控转台提供角速率输入。测试环境和测控系统如图12所示。硅微陀螺仪测控样机由两块四层板构成,上板由陀螺表头、模拟接口电路和激励电路组成,下板由ADC、DAC模块和基于FPGA的数字测控电路组成。

图12 测试环境和陀螺样机
现场测试时,将陀螺样机放置固定于温控转台中央,用工控机输入角速度。在温控转台设置温控程序步骤。两台电源通过滑环给陀螺样机提供所需的供电电压、调轴和调谐电压。RS422电平标准的差分线也通过滑环传输给上位机,在LabVIEW中图形化搭建接收程序,虚拟示波器显示数据,采样频率180 Hz。
3.2 力平衡模式测控系统性能测试
将硅微陀螺仪样机上电,放置10分钟稳定后,测试1个小时数据。AGC闭环中设计参考幅度为0.5 V,多次调试,选择合适PI参数,测试结果如图13(a)所示。在1个小时内,驱动幅度信号的标准差为62 μV,相对稳定性达124 ppm。如图13(b)所示,PLL设计中相位理想情况下应该为-90°,但是因为电路延迟、控制误差和截断误差的存在,在1个小时内,相位信号的标准差和相对稳定度分别7.1 m°和79.1 ppm。
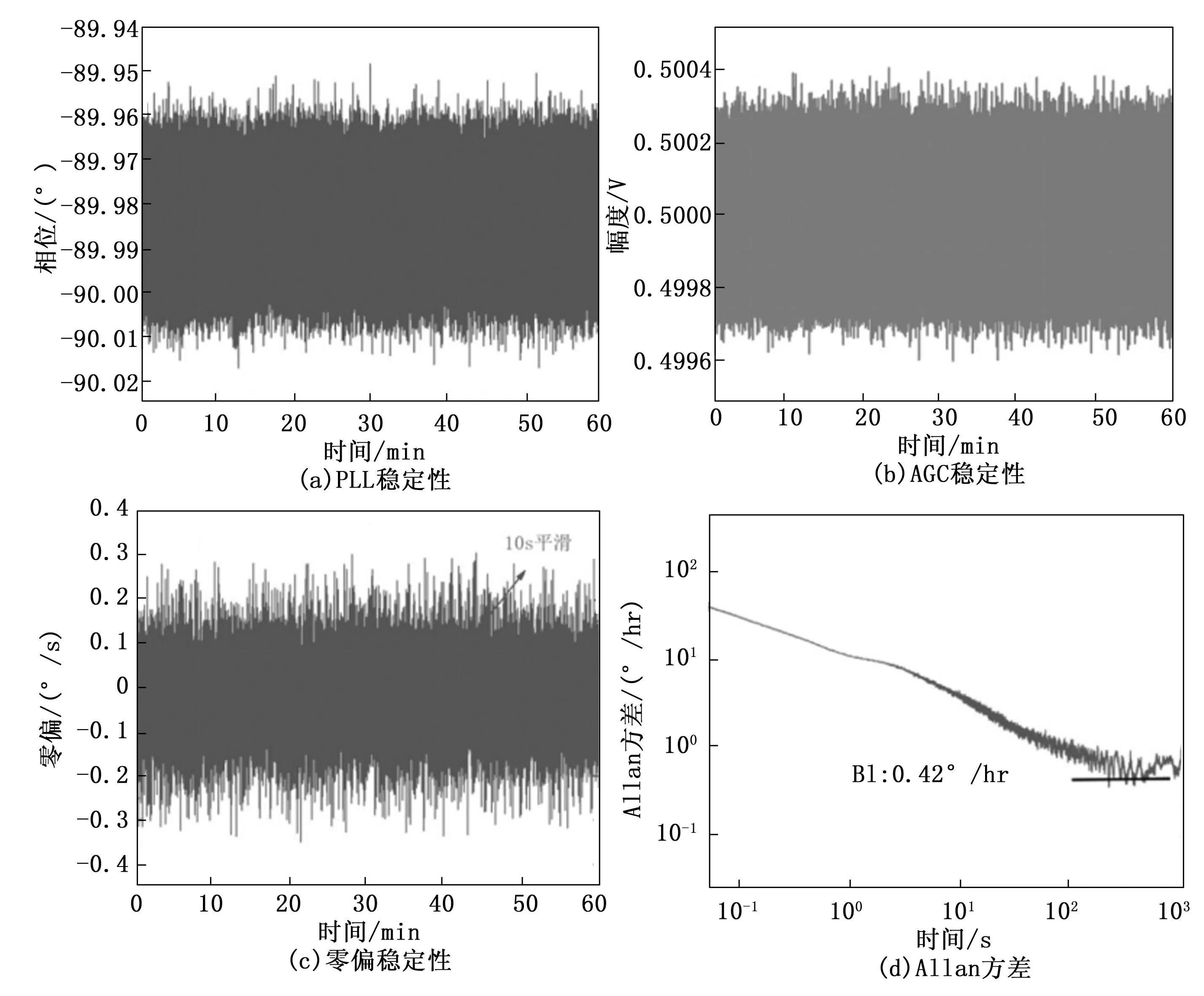
图13 输出性能测试图
根据《SJ 21266-2018 MEMS陀螺仪测试方法》,标度因数是输出量与期望量的变化量之比,单位一般为mV/(°/s)。
(16)

U=KΩ+b+ε
(17)
其中:Ω表述陀螺仪输入角速率,b为拟合零位,ε为拟合误差。用最小二乘法按式(16)~(19)计算标度因数SF。
(18)
(19)
其中:输出值和拟合直线的最大值绝对偏差|ΛU|max,计算|ΛU|max与陀螺最大量程的比值即为标度因数非线性Kn:
|ΛU|max=max[|Ui-(KΩi+b)|]
(20)
(21)
标度因数温度灵敏度是由工作温度变化引起的标度因数变化程度,标度因数温度灵敏度Kt计算公式如下:
(22)
其中:kmax和kmin表示工作温度范围内标度因数最大值和最小值,ktm为室温下标度因数;TH和TL表示工作温度上限和下限。
在外界无角速率输入情况下测得的陀螺仪零偏输出为:
(23)
其中:Ui为第i次采样时陀螺仪输出,N为采样率,K为标度因数,Q为平均输出值的个数。采用10 s平滑,1σ计算零偏稳定性。
采用科氏力闭环和正交校正闭环后,硅微陀螺仪样机放置稳定10分钟后,测试1小时,测试结果零偏和Allan方差如图13(c)、(d)所示。经过计算,零偏稳定性为2.9 °/h,由Allan方差可知零偏不稳定性为0.42 °/h,ARW为0.16 °/√h。
3.3 温度补偿实验
在0、10、20、30、40、50、60、65 ℃共8个温度点,测试不同温度点下驱动轴谐振频率。实验结果显示,驱动轴谐振频率和温度之间有较好的线性关系,采用线性拟合方法拟合出结果。
f(T)=-0.1253*T+5048
(24)
在0~65 ℃内相同的8个温度点,进行标度因数测试:±1、±5、±10、±30、±50、±100、±200、±300°/s。每个温度点在稳定半个小时后开始标度因数测试,每个速率点输出稳定后采集30 s数据,根据最小二乘法拟合得到标度因数和拟合零位。补偿前标度因数和温度之间近似线性关系。
SF(T)=1.025e×10-5T+0.005566
(25)
补偿的思路是将随温度不断变化的标度因数用谐振频率数学表达出来,在陀螺输出时除去这个表达式,将陀螺的标度因数归一化到1 °/s。再乘上设定的标度因数值0.005 6,即完成0~65 ℃下陀螺标度因数的温度补偿。采用线性补偿后标度因数温度灵敏度1 800 ppm/℃降至102 ppm/℃,提升1个数量级。
在0~65 ℃内,从0 ℃以1 min/℃升温速率升至65 ℃保持。在这个温度范围内零偏稳定性为17.7°/h,构建隐含3层BP神经网络,其中隐含层数12,进行零偏补偿,补偿后0~65 ℃内零偏稳定性降至9.1°//h。在设计了正交校正闭环后,硅微陀螺仪零偏性能大幅提升,但仍然有小幅度的漂移,采用BP神经网络温度补偿后性能提升近2倍。
4 结束语
本文基于FPGA采用Verilog 硬件描述语言对数字驱动闭环进行设计与实现,高稳定性的AGC和PLL为高精度输出提供了基础。在此基础上,对科氏力闭环和正交校正闭环设计实现功能,对正交误差的进行耦合刚度抵消,科氏力闭环实现高精度输出。测试结果表明,常温环境下,零偏稳定性为2.9 °/h。经过温度补偿后,在0~65 ℃变温范围内,零偏稳定性仍低于10 °/h,标度因数非线性为198 ppm,标度因数温度灵敏度大幅度降低。不仅提升了陀螺仪的温度性能,也为陀螺测控电路ASIC提供了便利途径。

