Symmetric Brownian motor subjected to L´evy noise
Kao Jia(贾考), Lan Hu(胡兰), and Linru Nie(聂林如)
Faculty of Science,Kunming University of Science and Technology,Kunming 650500,China
Keywords: symmetric Brownian motor,average velocity,energy conversion efficiency,L´evy noise
1.Introduction
Much attention has been paid to the energy problem to ensure continued development.[1]Since Smoluchowski and Feynman’s Gedanken experiment about converting thermal energy into useful work,[2]Brownian motors (BMs) have been intensively investigated due to their wide range of applications in bioengineering[3]and nanotechnology,zeolite,[4]cerebral cell,[5]environmental fractal dimension,[6]and so on.A symmetric BM based on the Feynman ratchet has been proposed,[7,8]which performs like a Carnot engine.Although Gaussian white noise is involved in many aspects,such as binocular rivalry,[9–11]transport of coupled BM,[12]simulated molecular dynamics,[13]stochastic gene transcriptional dynamics[14]and so on,BMs work with small current and low energy conversion efficiency due to Gaussian white noise.
In the action of a periodic force,particles in periodic potentials behave with anomalous transport behaviors.There are some instances where the periodic force induces multiple current reversals and absolute negative mobility in periodic potential systems.[15–20]Furthermore,noise-induced phenomena have prompted researchers to investigate stochastic systems with anomalous diffusions in recent years.[21–23]Continuoustime random walk,fractional Fokker–Plank equation and L´evy noise are frequently used to describe systems with anomalous diffusions.[24–27]Stochastic L´evy processes,which serve as paradigms for description of many unusual transport processes,are characterized by the mean squared displacement of their state variables〈(x(t)-〈x(t)〉)2〉 ∝tν(ν=2/α), whereαis the stable index.The motion of a free Brownian particle driven by L´evy noise belongs to superdiffusion for 0<α<2,subdiffusion forα>2, and normal diffusion forα=2.[28]The L´evy noise with anomalous diffusion involves many complex dynamical behaviors.L´evy noise causes multiple absolute negative mobilities in periodic potential systems.[29,30]For ratchet systems,symmetry breaking of the L´evy noise also induces multiple current reversals.[31,32]During the region of superdiffusion,there is a current maximum in the asymmetric flashing systems.[33]The authors of Ref.[34]investigated heat conduction in low-dimensional nonlinear lattices subjected to L´evy noise,and found that the noise generates anomalous thermal conduction.In particular,L´evy noise induces a divergent thermal conductivity with the system size forα<2 or a convergent thermal conductivity(or an insulator in the limit case)forα>2.However, the characteristic dynamical behaviors caused by L´evy noise have not been completely understood.In this paper,it will be seen that the current and energy conversion efficiency of the symmetric BM can be greatly enhanced in the case of L´evy noise or the L´evy noise can improve the operating performance of the symmetric BM.
We aim to investigate the effects of the L´evy noise on average velocity of the symmetric BM without load, its energy conversion efficiency in the case of load,and the measures for optimizing its operating performance.The rest of this paper is structured as follows.In Section 2,the model and theoretical analysis are provided.In Section 3,the results and discussion are presented.Finally,the conclusion is given in Section 4.
2.Model and theoretical analysis
In this section, we will consider the symmetric BM subjected to L´evy noises, which consists of two compartments connected by a spring, each of which contains blades and wheels, see Fig.1 from Ref.[7].The blades are driven by two independent temperature sources.The BM is characterized by a Carrot heat engine with two constant temperature heat baths.In this sense,the BM plays a role in transforming thermal energy into useful work.The transport of particle and energy in biological organisms and nanomachines can be realized via the BM.Previous research regarded the two heat baths as the Gaussian white noises, which resulted in a extremely low energy conversion efficiency.In contrast, here they are considered to be two independent L´evy noises, and therefore the case can be considerably improved.The stochastic differential equations describing the symmetric BM read

whereV0controls the height of the potential,anddis the number of teeth per cycle 2π.
Theξi(t)(i=1,2)in Eqs.(1)and(2)are the L´evy noises.There are many molecular BMs in biological systems, where the noises are usually assumed to be L´evy noises due to their complexity.[7,15,22]The statistical properties of L´evy noise can be specified according to the following characteristic function:

forα=1, whereD,αandβare the noise intensity, the stability index, and the symmetry parameter, respectively.The three main parameters vary within the regimesα ∈(0,2),β ∈[-1,1],andD ∈(0,∞).
Thus, the probability distributionLof the L´evy noise is given by
whereξrepresents the L´evy random variable.Theδassociated Gaussian white noise occurs only whenα= 2,which is a special case of the L´evy noise.
It is difficult to find an analytical expression of the system.Therefore, we will use numerical calculations to solve Eqs.(1) and (2).The numerical algorithm is obtained with a discrete time steph
whereαi(i=1,2)is the stability index of the L´evy noise andξi(i=1,2)is the L´evy random variable.
The time stephis chosen to be so small(e.g.,h=0.001)that the errors brought by the above Euler algorithm can be accepted.The random variableξicorresponding to the characteristic functions(6)and(7)can be generated using the Janicki–Weron algorithm.Forαi ̸=1,ξican be realized by the following method:[28]

In these equations,VandWdenote independent random variables; namely,Vbeing uniformly distributed in the interval(-π/2,π/2)andWbeing exponentially distributed with a unit mean.Here,letβ1=β2=β,and the noise is symmetric forβ=0,while it is asymmetric forβ ̸=0.Diis the intensity of the L´evy noise.
Thus,the mean velocity(or current)of the BM can be obtained numerically via Eqs.(1)–(12)according to its definition
where〈〉denotes the ensemble averaging.In the hypothesis of ergodicity,the time averaging is equal to the ensemble averaging.In the process of computing〈v〉,500 different trajectories were run,and each trajectory was evolved fort=2×104.
The physical mechanism of the BM is similar to that of the Carrot heat engine, where its input total energy from the compartment with a higher noise intensity is passed to the other compartment with a lower noise intensity through the coupling spring.Some of them are then used to lift the loadτor do useful work,and the others are dissipated.The useful work is given by
wheretiandtfare the initial time and the final time, respectively.The input total energy can be obtained by

which can reflect the operating performance of the BM.By adjusting the parameters of the L´evy noise,the energy conversion efficiency can be maximized to optimize the BM.

Fig.1.Schematic diagram of a symmetric Brownian motor.
3.Results and discussion
The current and the energy conversion efficiency of the symmetric BM can be computed numerically at different parameters of the L´evy noise via Eqs.(1)–(17).The results are plotted in Figs.2–6.The operating performance of the BM will be discussed in the following two cases.
Let us first discuss the case where the load is not suspended under the BM, i.e.,τ= 0.Figure 2 shows the dependence of the average velocity〈v〉(or current)on the phase shiftφat different symmetry parameters:β=-1,0,1.The other parameters areα1=α2=1.2,V0=3,d=4,k=100,D1=1, andD2/D1=2.Here, letktake a great value (e.g.,100), which means that there is a rigid coupling between the two compartments of the BM.From Fig.2, the current oscillates periodically with the phase shift and its amplitude is greatly affected by the symmetry parameter of the L´evy noise.Asβ=0,-1, the〈v〉 is both very small and negative.This means that the system is not used to lift the load and does not play a role of BM forα1=α2=1.2.However,forβ=1,the amplitude of the〈v〉is the greatest and its direction is always greater than zero.Therefore,the asymmetric L´evy noise withβ=1 can enhance the current of the BM forα1=α2=1.2 if the phase shift takes an optimal value.In what follows,the noise symmetry breaking withβ=1 will be addressed.
The factors causing symmetry breaking in the system are the ratchet potentialV,the noise intensity difference,the load,and the noise symmetry parameterβ.Therefore,the direction of the system’s current is mainly determined by a combination of them.It is generally thought that adjusting the phase shiftφcan let the〈v〉 be positive forD2/D1=2 andβ=0.Nevertheless, it is worth noting that in Fig.2 the average velocity forβ=0 is always negative, even thoughD2/D1>1.This means the stable state index of the noise also can change the symmetry of the system,and induce current reversal of the system.
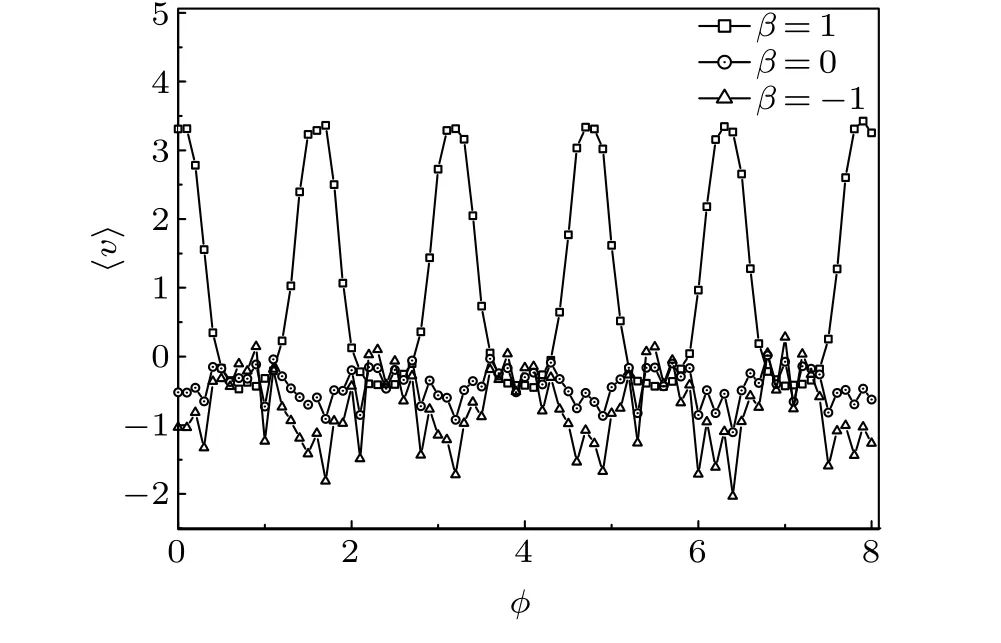
Fig.2.The dependence of the average velocity〈v〉on the phase shift φ at different symmetry parameters: β =-1,0,1.The other parameters are α1=α2=1.2,V0=3,d=4,k=100,D2/D1=2,D1=1,and τ =0.

Fig.3.The〈v〉versus φ at different stability indexes: α1 =α2 =1.2,1.5,1.8,2,with β =1,φ =1.7.The other parameters are the same as those in Fig.2.
To illustrate the effect of the stability indexes of the L´evy noises, the〈v〉 versusφat different stability indexes, i.e.,α1=α2= 1.2,1.5,1.8,2, in the asymmetric caseβ= 1 is shown in Fig.3.In the computing process, it was found that when the stability indexαi<1(i=1,2),the state variables of the system fluctuate very seriously and have heavier tails.[35]Thus, the region ofαi ≥1 will be discussed here.Figure 3 shows that the smaller the stability indexes,the greater the amplitude of the〈v〉versusφ.For smaller stability indexes(e.g.,α1=α2= 1.2), choosing an optimal phase shift can make the BM possess a greater positive current.It is well-known that the L´evy noise causes superdiffusion of free overdamped particle forαi ∈(0,2), subdiffusion forαi ∈(2,∞), and normal diffusion forαi=2.[28]In other words, the L´evy noises with anomalous diffusions can enhance the current of the BM.With the increment ofαi(e.g.,α1=α2=2), the〈v〉 oscillates slightly near the horizontal axis ofφ.It is very difficult to pick out contribution of the asymmetry of the L´evy noiseβ=1 from the curve ofα1=α2=2 in Fig.3.Thus, it is deduced that the amplitude of〈v〉versusφforαi>2 will be smaller than that forαi=2.Therefore,an interesting conclusion can be made: the L´evy noises with smaller stable indexes in the serious symmetry breakingβ=1 can enhance the positive current of the BM.

Fig.4.The〈v〉versus D2/D1 at different stability indexes:α1=α2=1.2,1.5,1.8,2 for(a);α1=1,α2=1.2,1.5,1.8,2 for(b);α1=1.2,1.5,1.8,2,α2=2 for(c).The other parameters are the same as those in Fig.3.
Since the stability indexes of the two noise sources are equal to each other, the〈v〉versus the ratio of noise intensityD2/D1is drawn in Fig.4(a).From Fig.4(a) we can see that the stability indexes also affect the curves of〈v〉versusD2/D1.Forα1=α2=2, i.e., the noises with normal diffusions,〈v〉versusD2/D1exhibits a very low peak.This result agrees with that in Ref.[7].With the decrement of the stability indexes(e.g.,α1=α2=1.5),the peak becomes higher and gradually shifts to the negative direction of theD2/D1axis.The〈v〉is still greater than zero asD2/D1≤10 due to the symmetry breakings by the phase shift and the noise symmetry parameterβ=1.The left-hand shift of the peak happens because the smaller stability indexes can bring about greater fluctuations in the system.As the stability indexes are decreased further,e.g.,α1=α2=1.2,the direction of〈v〉changes from positive to negative withD2/D1increasing, namely, a current reversal phenomenon.It is inferred that the reversal point becomes smaller with the decrement of the stability indexes.The current reversal phenomenon should be attributed to nonlinearity of the real noise intensityDαi,β,Diin Eq.(12)withαi.
The symmetry breaking between the stability indexes of the two L´evy noises also influences the current of the system.Figure 4(b)shows the curves of〈v〉versusD2/D1at differentα2=1.2,1.5,1.8,2 with the fixedα1=1.Figure 4(b)shows that the peak of〈v〉 versusD2/D1gradually goes up withα2decreasing,and its value is much greater than that in the case ofα1=α2.The L´evy noise forαi=1 causes ballistic diffusion of free overdamped particles.In other words, the L´evy noises with ballistic diffusions can enhance the positive current of the BM to a large degree.Letα2=2 unchanged(see Fig.4(c)).However, no matter how muchα1takes, the positive current of the system is much smaller than that in Fig.4(b).This means that the L´evy noises withαi=2 can weaken the positive current of the system.
The case ofτ ̸=0 will be addressed next.Figure 5 shows the dependence of〈v〉on the loadτat some stability indexes:α1=α2=1.2,1.5,1.8,2.From Fig.5,we can see that the〈v〉decreases as the load increases.The lighter load can only be elevated by the BM subjected to the L´evy noises with normal diffusionsαi=2,while the heavier load can only be elevated by the BM with the L´evy noises withαi<2.Thus, energy conversion efficiency of the BM driven by the L´evy noises with smaller stable indexes is obviously higher than that of the BM by the L´evy noises withαi=2,see Fig.6.In particular, adjusting the stable indexes of L´evy noises can enhance the energy conversion efficiency of the symmetric BM.Note that asD2/D1=2, the curve of the efficiencyηwithτforα1=α2=1.2 is much lower than that forα1=α2=1.5.However, the〈v〉 forα1=α2=1.2 is greater than that forα1=α2=1.5 asτ=0, see Fig.4(a).Therefore, in the region of superdiffusion,the L´evy noises with optimal stability indexes can let the BM achieve the highest energy conversion efficiency.In addition,it is deduced that ballistic diffusion can make the symmetric BM possess greater current but lower energy conversion efficiency.
In the following,the intrinsic physical mechanism of the symmetric BM will be discussed.Compared with the system considered in Ref.[7],the difference is that the noise sources used here are two L´evy noises, not Gaussian white noises.The last termh1/αiηi(t) in Eqs.(9) and (10), which has the same expression as the free Brownian particle by the L´evy noise, plays a very important role in determining the dynamical behaviors of the system.The stable index of the L´evy noise is smaller than 2, the free Brownian particle will make a superdiffusive motion, while it will make a normal diffusive motion forαi=2.This is equivalent to increments of the noise intensitiesDiin Eq.(12) in contrast to the case ofαi=2.Therefore, the greater current of the BM can only be achieved in the case of symmetry breaking (e.g.,β=1).Of course,the symmetry breaking and the smaller stable indexes also enhance the energy conversion efficiency of the BM.The nonlinearity of the energy conversion efficiency with the stable indexes in Eq.(17)brings about the nonmonotonicity ofη.It is worth noting that the very low efficiencies in Fig.6 result from the ratchet potential described by Eq.(3).However,the efficiencies are close to 1 if the potential of system is chosen as a flashing ratchet potential.
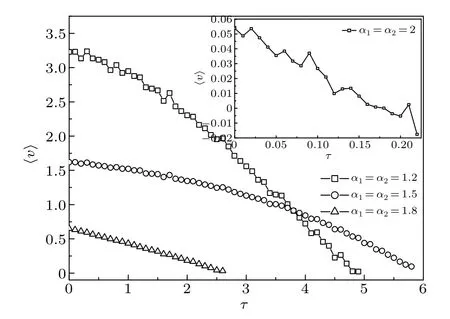
Fig.5.The〈v〉versus the load τ at different stability indexes: α1=α2=1.2, 1.5, 1.8, 2 with D2/D1 =2.The other parameters are the same as those in Fig.3.
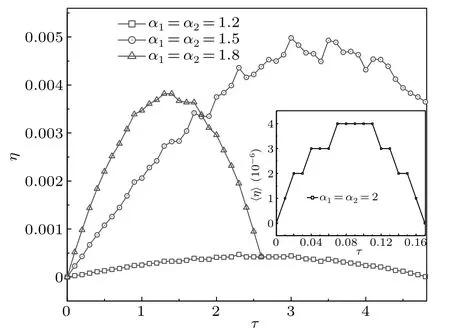
Fig.6.The energy conversion efficiency η versus τ at different stability indexes:α1=α2=1.2,1.5,1.8,2 with D2/D1=2.The other parameters are the same as those in Fig.5.
4.Conclusion
Most researchers previously studied the operating performance of the BM driven by the Gaussian noises.In this paper, we have investigated effects of the L´evy noises on the current and the energy conversion efficiency of the symmetric BM.Our results indicate that the BM subjected to the L´evy noises with smaller stable indexes can work in the greater current without the load and the higher energy conversion efficiency with the load than that subjected to the L´evy noises withαi=2.This means that the noises with superdiffusions can better improve the operating performance of the BM.However,the prerequisite is that the L´evy noises must be those with symmetry breaking.For the ratchet potential of the systemVR(θ)(see Eq.(4)),the noise symmetry parameterβtakes 1,while-1 for-VR(θ).Sinceα1=α2=2(i.e.,the L´evy noises with normal diffusion),the current of the BM is not sensitive to the noise symmetry parameterβ.Yet, for the L´evy noises with superdiffusions, the symmetry breaking can let the BM be the best operating state.In symmetry breaking, the L´evy noises withαi=1 can make the BM achieve a greater current but it does not acquire a better energy conversion efficiency.In addition,the nonlinearity of the real noise intensities of the L´evy noises with their stability indexes can induce the current reversal of the system aboutD2/D1.Of course, for the L´evy noises withαi>2 the BM will lose its intrinsic essence due to the smallest fluctuations in it,and it has no potential research significance.Experimentally, we let a Gaussian white noise drive an RLC circuit and obtain a harmonic noise.Then, applying the harmonic noise to a system with ratchet periodic potential can generate an abnormal diffusion with diffusive indexν.Thus, according toα=2/ν, control of the stability index is realized by adjusting the parameters of the RLC circuit.
The BM usually exists in some nanoscale machines and organisms.Greater current and higher energy conversion efficiency of the BM are very important for them to perform normally.Our research results not only have crucial significance in understanding performance mechanisms of nanomachines and organisms but they also provide a theoretical basis for experimentally improving the performance of the symmetric BM.
Acknowledgments
Project supported by the Research Group of Nonequilibrium Statistics (Grant No.14078206) and Kunming University of Science and Technology,China.
- Chinese Physics B的其它文章
- Unconventional photon blockade in the two-photon Jaynes–Cummings model with two-frequency cavity drivings and atom driving
- Effective dynamics for a spin-1/2 particle constrained to a curved layer with inhomogeneous thickness
- Genuine entanglement under squeezed generalized amplitude damping channels with memory
- Quantum algorithm for minimum dominating set problem with circuit design
- Protected simultaneous quantum remote state preparation scheme by weak and reversal measurements in noisy environments
- Gray code based gradient-free optimization algorithm for parameterized quantum circuit

