Protected simultaneous quantum remote state preparation scheme by weak and reversal measurements in noisy environments

Mandal Manoj Kumar, Choudhury Binayak S., and Samanta Soumen

Department of Mathematics,Indian Institute of Engineering Science and Technology,Shibpur B.Garden,Howrah 711103,West Bengal,India

Keywords: multi-qubit entangled channel, quantum remote state preparation, noisy environments, weak and reversal measurements

1.Introduction

In this paper, our basic program is to present a protocol for simultaneous remote preparation of a one-qubit and a twoqubit state at a distant location where the preparations are intended by two different parties.It is a remote state preparation protocol which belongs to a different category of quantum communication schemes compared to teleportation, the basic difference between the two is that in the former the states to be remotely created are known to the parties who intend to create them while in the latter the states intended for transfer are totally unknown to the senders in the protocol.The teleportation protocol was first proposed by Bennettet al.[1]in 1993.It is supposed that quantum communication science was initiated in this particular work.Remote state preparation protocol came into being through the work of Lo[2]in 2000.Both these types of protocols have several variations and are applied to very wide varieties of quantum states.References[3–14]are some instances from the literature on quantum teleportation while[15–22]are works on remote state preparation protocols.Particularly, in this paper we present a remote state preparation protocol in which there are two parties Alice and Candy whose intentions are to create a single-qubit and a two-qubit state respectively in the laboratory of Bob.The protocol is executed by utilizing a five-qubit entangled state shared between Alice,Bob and Candy where Bob holds three-qubits while Alice and Candy hold one-qubit each.

Our protocol is included in the program of multi-tasking quantum communications which is that through a single protocol, more than one quantum communication tasks are performed.These types of works have appeared in a good number of recent articles.Bidirectional teleportation in which the simultaneous exchange of two quantum states takes place was discussed by Jianget al.[23]in 2021, Wanget al.[24]in 2021 and Verma[25]in 2021.Quantum conference protocols have appeared in works by Banerjeeet al.[26]in 2018, Choudhuryet al.[27]in 2022,etc.A hybrid protocol involving both remote state preparation and quantum teleportation was presented by Choudhuryet al.[28]in 2023.In all these multi-tasking protocols, there is an unavoidable requirement for entanglement resources involving a high number of qubits shared amongst the parties participating in the protocol.This is a challenge for quantum communication science since multipartite entanglement is difficult to produce and,even if produced,they are susceptible to environmental noise due to which the communication protocol may develop unreliability to a certain extent.There are certain methods for minimizing the effect of such noises such as quantum error correction,[29–31]entanglement purification,[32,33]weak and reversal measurements,[34–41]etc.The ideal noiseless case is discussed,following which the effect of amplitude-damping noise is considered.It is shown by analysis of specific cases that the fidelity of the protocol decreases with the increase in the noise parameter.Further, by performing weak and reversal measurements,we observe that the effect of noise can be minimized.

The present protocol is a demonstration of performing two remote state preparation tasks through a single protocol by utilization of a single entangled resource.There can be different ways of performing the same tasks,for instance,two separate entangled channels of two-qubits and three-qubits can be utilized here.But that would be the case of exactly two separate protocols.Our objective here is to use a single integrated protocol where Bob finally executes unitary operations on the basis of the classical communications jointly received from Alice and Candy.

Quantum communication protocols have a vast range of applications.Its versatility extends to various fields within the realm of quantum information science, facilitating advancements in quantum communication and enabling new possibilities in quantum computation such as quantum key distribution,[42–52]quantum secure dense coding,[53,54]etc.

For experimental aspects of the implementation of weak and reversal measurements, we refer to Ref.[55] and references therein.

In the present case we use a five-qubit entangled state as a quantum channel.We describe the generation of this entanglement resource and execute the circuit algorithm on the IBMQ platform.[56,57]We consider the effect of amplitude-damping noise on the protocol and show that the effect of such noise can be minimized by executing weak and reversal measurements.

2.Remote state preparation with two senders and one receiver

Suppose there are three parties namely, Alice, Bob and Candy.Also,there are two quantum states

In this scenario suppose Alice wants to create the quantum state|M1〉 at Bob’s laboratory and also at the same time Candy wants to create the quantum state|M2〉at Bob’s site using a single entangled resource given in Eq.(2) (see below).The sender Alice knows the information about the state|M1〉and Candy knows the information about the state|M2〉,that is,the coefficients (α0,α1) and (β0,β1) are known to Alice and Candy,respectively.

There is a maximally entangled state amongst three parties which serves as the quantum resource which is given by

where the particlea1belongs to Alice, particlec1belongs to Candy and particles (b1,b2,b3) are in the hands of Bob.The above-mentioned task of quantum information transfer is to be accomplished using the quantum channel Eq.(2).Here the state|M1〉and|M2〉intended for creation at Bob’s site is possessed by none of the parties.

Alice prepares a basis for a possible measurement on her qubita1given by

Alice and Candy perform measurements on the qubitsa1andc1,respectively.After the measurements of Alice and Candy,they transmit their outcomes to Bob utilizing two separate 1-bit classical communication channels.According to the measurement results, Bob applies a suitable sequence of unitary operations on his three particles to get the intended states.The details of the sender’s measurement outcomes and corresponding unitary operations are given in Table 1.After using unitary operations all the possible reduced states can be written as (α0|0〉+α1|1〉)b1⊗(β0|00〉+β1|11〉)b2b3.This is the end of the protocol.

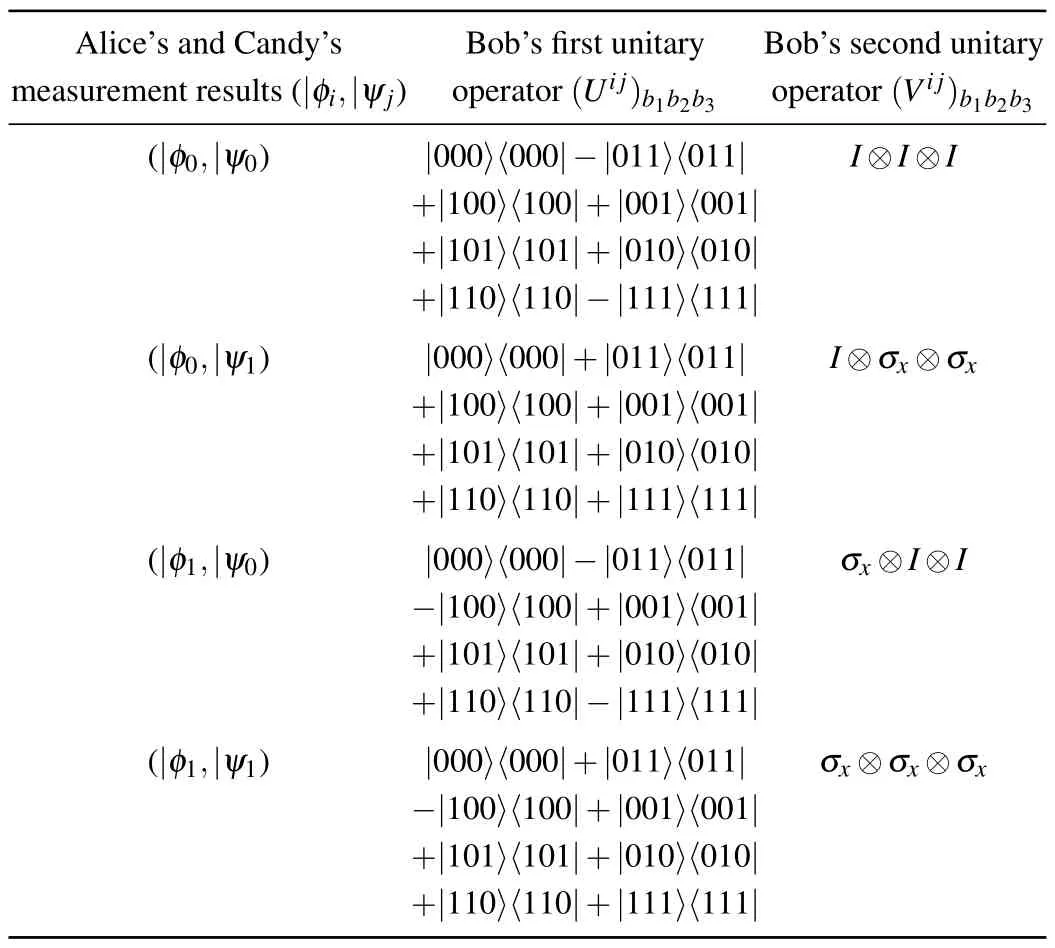
Table 1.Outcome results and corresponding unitary operators.

As an illustration, using the basis given in Eq.(3) the quantum channel|τ〉in Eq.(2)can be written as

Now Bob first applies a unitary operator (|000〉〈000|+|011〉〈100| +|100〉〈100| +|001〉〈001| +|101〉〈101| +|010〉〈010|+|110〉〈110|-|111〉〈111|) on the state of the qubitsb1,b2, andb3.After that Bob applies another unitary operatorI ⊗σx ⊗σxon his qubitsb1,b2, andb3.Then the final state of the qubitsb1,b2, andb3becomes(α0β1|011〉+α0β0|000〉+α1β1|111〉+α1β0|100〉)b1b2b3=(α0|0〉+α1|1〉)b1⊗(β0|00〉+β1|11〉)b2b3.This is the end of the protocol.

3.Preparation of entangled channel

The circuit for generating the quantum state|τ〉in Eq.(2)is given in Fig.1.It is generated by utilizing two Hadamard gates,four CNOT gates and one Z-gate.

Initially,a five-qubit state is prepared with five zero initial states as

In the next step, one CNOT gate is applied with qubit 1 as the control qubit and qubit 3 as the target.Again two CNOT gates are applied with qubit 2 as the control qubit for each of qubits 4 and 5, respectively.Lastly, one Z-gate is applied on the qubit 2.Then the state|X3〉of five-qubits is transferred to gain one Hadamard gate is applied on qubit 2, then the state|X2〉of five-qubits becomes

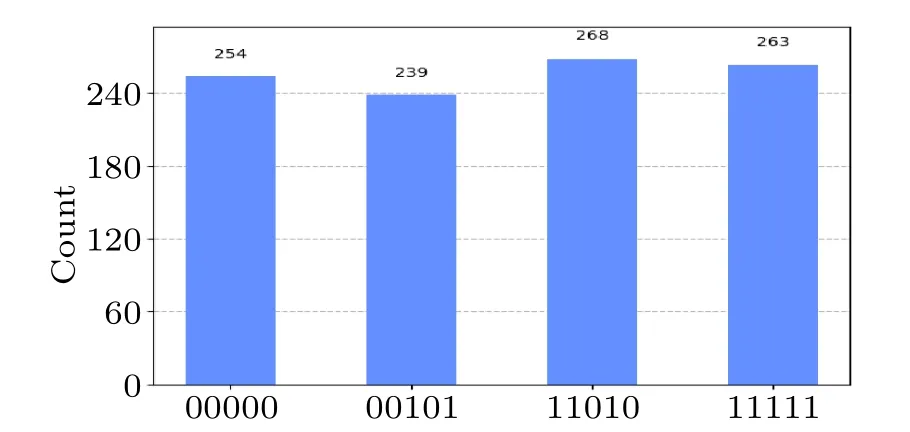
Fig.2.Output of the quantum circuit in Fig.1 on IBMQ.

Fig.3.Bloch sphere representation of the output of the circuit in Fig.1.

4.Effect of noise in the protocol

From the experimental point of view, a real quantum state will couple inevitably with its surrounding environment which disturbs the coherence of the entangled channel and produces an environmental noise.The quantum entangled channel which is the fundamental ingredient for the purpose of a remote state preparation scheme between two distant parties is completely affected by the environmental noise during the distribution of qubits amongst the entangled parties.As a result,the performance of the present remote state preparation protocol is decreased.In this section,we discuss the effect of noise in our proposed remote state preparation scheme.

To minimize the influence of quantum noise,as much as possible, we suppose that the receiver Bob creates the fivequbit entangled state|τ〉a1c1b1b2b3in his laboratory and distributes qubita1to Alice and qubitc1to Candy.Also, we assume that in the process of distribution of qubits, only two qubits go through amplitude damping noisy channel and qubitsb1,b2,b3are not affected by this noise since these are not transmitted.

The density matrix of the corresponding entangled channel(2)can be written asρ=|τ〉a1c1b1b2b3〈τ|and,after passing through the noisy environment,the corresponding density matrix evolves as

whereKis are the Kraus operators satisfying ∑i K†i Ki=Iand†stands for the conjugate transpose of a matrix.

4.1.Simultaneous remote state preparation protocol via amplitude damping noise

In this subsection, we particularly analyze the effect of amplitude damping (AD) noise in the simultaneous remote state preparation scheme.The Kraus operators of the AD noise are defined as[36]

wherek ∈[0,1]represents the decoherence rate of AD noise.

In this protocol,Bob prepares the 5-qubit entangled channel in his laboratory and distributes the qubitsa1andc1to Alice and Candy respectively through AD noisy environment.Also,suppose that during the distribution process,these qubits pass through all possible AD noise.Then the corresponding density matrix of the transformed channel evolves in the following way:Now Alice and Candy perform their measurement with the basis given in Eqs.(3)and(4)and transmit the measurement results to Bob via 1-bit classical channels, respectively.After obtaining all the measurement results,Bob performs appropriate unitary operations with his qubits to get the desired state which both Alice and Candy want to create at Bob’s laboratory.

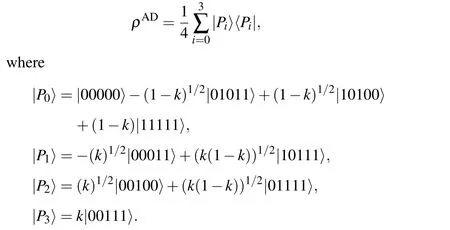
As an illustration,suppose Alice’s and Candy’s measurement results be|φ0〉a1and|ψ1〉c1,respectively.Then,according to the Eq.(6), the density matrix of the final output state reduces to

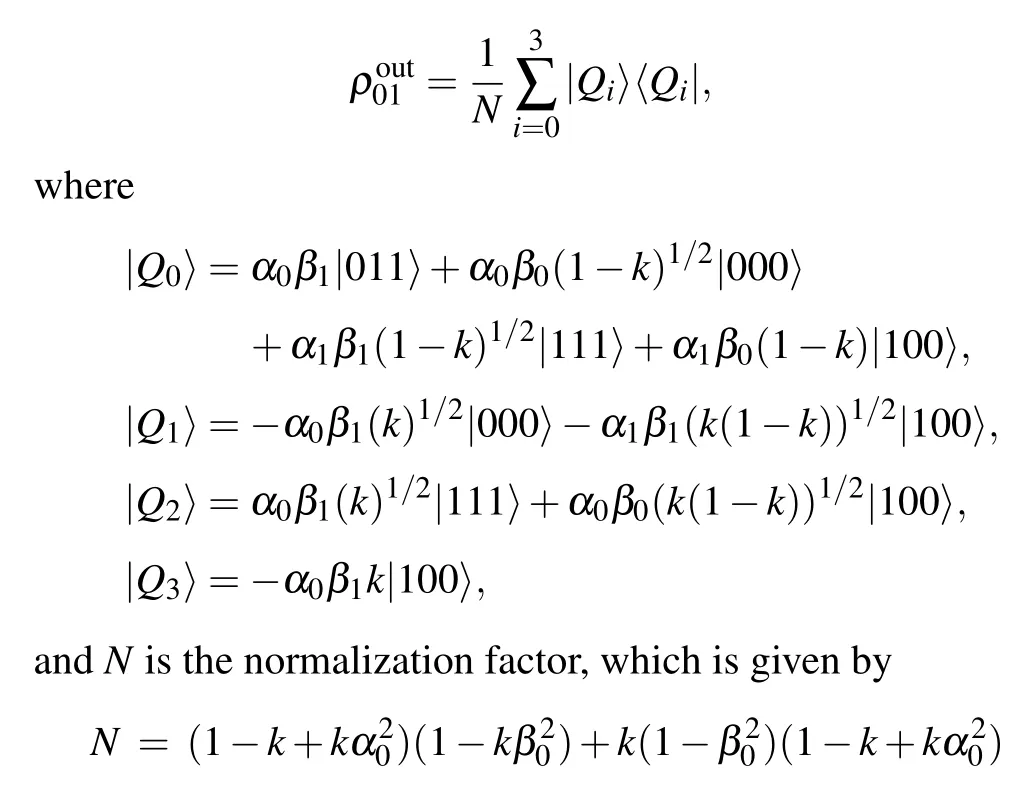
In Fig.4,we examine the changes in fidelityF1as we vary different parameters.Figure 4(a) demonstrates that when the noise strengthk=0.5, fidelity decreases asα0increases, but it increases with the increment ofβ0.Figures 4(b)–4(d)illustrate that fidelity consistently decreases as the noise strength increases.In the upcoming section,we will explore the incorporation of weak and reversal measurements to enhance the fidelity of our scheme.

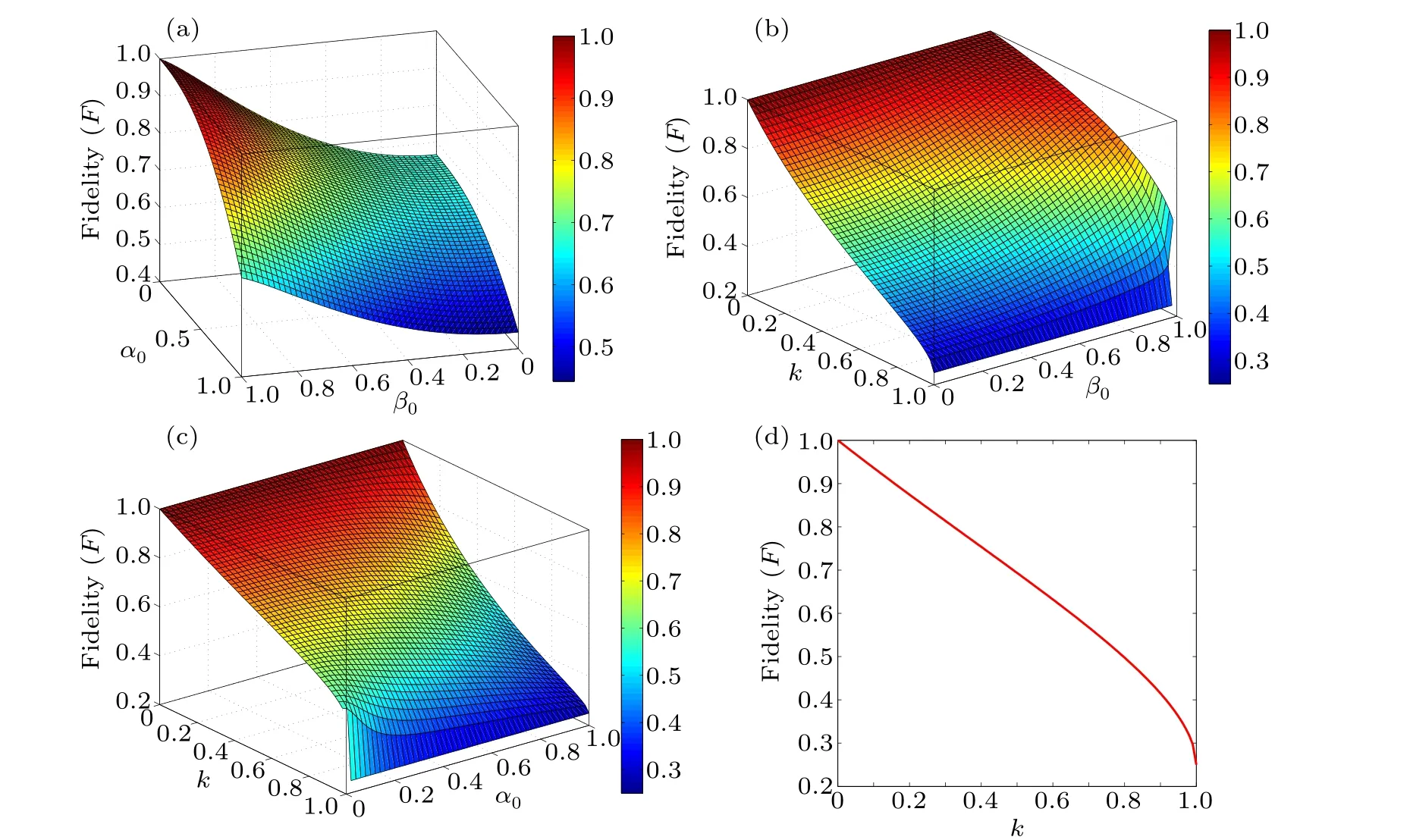
Fig.4.(a)Variation offidelity F1 with α0 andβ0 whenk√=0.5.(b)Variationof fidelity F1 withβ0andkwhen|M1〉=(0.4|0〉+0.6|1〉).(√c)Variation offidelityF1 with α0 and k when|M2〉=(0.3|000〉+0.7|111〉).(d)Variation of fidelityF1withk when|M1〉=(0.4|0〉+0.6|1〉)and|M2〉=(0.3|000〉+0.7|111〉).

5.Protected remote state preparation protocol via weak and reversal measurement

Here we discuss the performance of weak and reversal measurements regarding the fidelity of our protocol.To protect the entangled resource, first weak measurements are carried out on the qubits before they are transmitted and reversal measurements are performed after the distribution of qubits to the respective parties.

The weak measurement and the corresponding reversal measurement operators on a single-qubit system can be expressed as[35]

Now Bob distributes the qubitsa1andc1to Alice and Candy respectively and during this transmission qubitsa1andc1pass through AD noisy environment.Then according to Eq.(5),the density matrix of the state(12)is evolved into

After that, Alice and Candy execute their measurement with the basis given in Eqs.(3) and (4) and transmit the measurement outcomes to Bob via 1-bit classical channels, respectively.After receiving all the measurement outcomes, Bob performs appropriate unitary operations with his qubits to get the original states which both Alice and Candy want to prepare at Bob’s laboratory.

As an illustration,suppose Alice’s and Candy’s measurement results be|φ0〉a1and|ψ1〉c1respectively.Then,according to Eq.(6), the density matrix of the final output state reduces to

In Fig.5,we represent the fidelity with and without weak and reversal measurements for specific values of the parameters.The figures show improvements in fidelity after executions of weak and reversal measurements in all the considered cases.

The total success probability for the protection of the scheme against noise can be calculated by taking the trace of the entangled channel after entanglement sharing is completed.[58]

In the ideal noiseless condition, the total success probability of our scheme is

Also, in AD noisy environment (without weak and reversal measurements),the total success probability of our scheme is

But in the case when weak and reversal measurement is performed to increase the fidelity of our scheme,the total success probability is

Figure 5 shows that the application of weak and reversal measurements improves the fidelity of our protocol.The utilization of weak and reversal measurements enhances the fidelity of our protocol compared to scenarios affected solely by AD noise.A comparison between Figs.6(a) and 6(b) reveals the interesting feature that in the case whenk=0,the fidelity is always of value 1 while success probability decreases with an increase inkw.But with an increase in the value ofk,for fixedkw,the fidelity decreases while the success probability also decreases.Thus there is an inverse trade-off between fidelity and our failure to control the environmental noise.

Fig.5.(a) Variation of fidelity F1 and FOP 2 with a0 and b0 when k = 0.5, kw = 0.3.(b) Variation of fidelity F1 and FOP 2 with b0 and k when|M1〉= (√0.4|0〉+√0.6|1〉) and kw = 0.3.(c) Variation of fidelity F1 and FOP 2 with a0 and k when |M2〉= (√0.3|000〉+√0.7|111〉) and kw = 0.3.(d) Variation of fidelity F1 and FOP 2 with k when |M1〉= (√0.4|0〉+√0.6|1〉), |M2〉= (√0.3|000〉+√0.7|111〉) and kw = 0.3.Here all the upper curves represent optimal fidelity (FOP 2 ) with weak and reversal measurements while lower curves represent fidelity F1.

Fig.6.(a)Variationof fidelityF1andF2OPwith kw and k when|M1〉=(0.4|0〉+0.6|1〉),|M2〉=(0.3|000〉+0.7|111〉).(b)Variation of successprobabilitywith respect to k andkw.

6.Discussion and conclusion

We observe the fact that more deviation from the pure entangled resource has an adverse effect on fidelity.This has a physical implication that pure entangled states are better suitable for teleportation purposes.The noise may have different physical origins, which should bear a complex relationship with the performance of the protocol.In quantum systems, noise can arise due to random interactions with the environment and cause the system to lose coherence,leading to the degradation of quantum states.As the noise parameter increases, the rate of decoherence also increases, resulting in a decrease in fidelity.

In this paper, our final observation through Fig.5 is that amplitude damping noise can be controlled successfully to some extent by employing weak and reversal measurements.Noise is unavoidable in a communication system.Any realistic picture of communication protocol must involve the effect of noise.For a reliable system of communication,the analysis and control of noise is very important.Here we have considered amplitude damping noise but there are several other types of noises like phase-flip, bit-flip, bit-phase flip, phase damping,etc.which are also modeled with the help of appropriate Kraus operators.A particular feature of the noise analysis,as it appears in Fig.4, shows that the fidelity tends to 1 as the noise parameter goes to zero,which is what should be expected.Remarkably,the fidelity,albeit low,is never zero,even if the noise parameter is at its maximum.

Acknowledgment

Project supported by Indian Institute of Engineering Science and Technology,Shibpur,India.