低温共烧陶瓷激光测厚系统设计与误差分析

张铮, 薛波, 金子博, 邱达河

(湖北工业大学机械工程学院, 武汉 430068)

低温共烧陶瓷(low temperature co-fired ceramic,LTCC)是一种通过叠片和层压陶瓷生片,将多层印刷线路图形的立体拼接而形成的陶瓷电路基板,以集成电路技术为基础,迎合了电子元器件小型化、高频化、集成化的发展潮流,具备广阔的应用市场[1-2]。由陶瓷生片作为基础材料组成的陶瓷基板,作为产品其层压前后的厚度数据可以直观反映压机的工作状态和产品的质量优劣,是一项重要的质量指标[3]。因此,研发一种高精度的在线无损检测系统,确保LTCC制作过程的高效率和最终产品的高成品率,是具有重要意义的。

目前,工业化厚度测量的方法和系统较多,比较常用的有机械式测量、超声波测量和激光测量等,不同测量方式有各自的特点和适用场合。机械式测量方面,英国真尚有公司研制了一款CHY-C2A机械式测厚仪器,分辨率达到0.1 μm[4];中国中慧天诚科技有限公司研发了JS-QCHY-5机械测厚仪测量精度≤5 μm[5]。但由于是通过压力进行接触式测量,不适合柔性材料。超声波测量为非接触测量,以声压反射系数谱为依据,可以测量多种类薄层厚度。刘姝麟等[6]设计了一款超声波涂层测厚系统,能快速准确测量厚度。Janez等[7]利用激光脉冲在试样表面产生超声波,可以精准分析板的厚度和两板表面的凹凸度。但测量多层材料时易受干扰,导致测量精度失准甚至无法测量,且对使用环境要求严格。而激光测量作为非接触测量中的主流之一,安全可靠,精度高,更加适合陶瓷基板无损检测的需求。

激光测距技术高速发展,主要有脉冲法、相位法、三角反射法等。詹道桦等[8]提出了一种基于全相位傅里叶变换(all phasefast Fourier transform,apFFT)的相位式激光测距系统,具有良好的稳定性和抑制频谱泄露能力,但此设备成本较高。许敏娟[9]基于三角反射法设计一种双轨式钢轨测距仪,具备测量数据全程记录、回放、分析等功能,但对操作者的要求较高。针对目前市场测厚系统精度不高,测量数据易丢失等问题,基于激光相位测距的原理,设计一款双激光同轴位移测厚系统, 在对系统检测精度、效率与可追溯性等方面改进的同时,分析并消除产生的精度误差,通过取证该系统性能优于流行的激光测厚器。

1 LTCC激光测厚系统本原理

1.1 总体设计方案

LTCC激光测厚系统的总体结构如图1所示,本系统由定点采集部分和数据处理部分构成,定点采集部分包括激光测量模组和机械定位模组,数据处理部分包括可编程逻辑控制器(programmable logic controller,PLC)控制模组和上位机。

图1 LTCC激光测厚系统Fig.1 LTCC laser thickness measurement system

定点采集部分由激光测量模组和机械定位模组组成,激光测量模组包括激光传感器和传感器控制器;机械定位模组包括XY运动模块和定位治具,XY运动模块带动定位治具在水平面的X轴方向与Y轴方向运动,X轴行程250 mm,Y轴行程250 mm。在测量过程中,将陶瓷基板放入定位治具中,经由一侧定位,另一侧弹片固定,治具在XY运动模块的带动下,根据需要测量多个测量点;双激光位移传感器按序读取定位点数据,并传输到PLC控制模组,PLC控制模组同时将数据与位置信息上传到上位机,在上位机中完成厚度数据的分析处理。

1.2 激光测量模组

为保障激光测量模组的测量精度,需两个激光传感器的光束同轴、数据同步。本系统采用厚度测量用调整夹具固定传感器探头,可以向三坐标轴6个方向调整探头的空间位置,具体如图2所示。

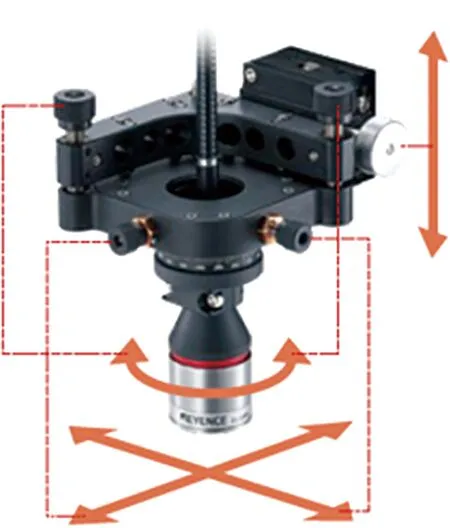
图2 厚度测量用调整夹具Fig.2 Adjustment jig for thickness measurement

同轴方面,调整激光传感器探头位置并保持装置稳定,在激光传感器的测量点处上固定一标准量块,采集其两侧表面的位置信息,通过最小二乘法处理数据,计算出上、下两条理想轴线;进一步地,通过理想轴线调整传感器自身的Z坐标轴,达到大致的同轴状态;校准完毕后,将标准量块替换成陶瓷基板,采集两侧表面测量点的位置信息,将下坐标系的数据换算到上坐标系中,通过数据分析计算出传感器此时的理想轴线和公共基准轴线,得出剩下的同轴度误差。将得到的同轴度误差将代入系统算法参数中,减小其引起的误差[10]。

同轴度误差具体计算步骤如下,假设标准量块上表面在上激光传感器中的测量坐标系中的方向向量为a(a1,a2,a3),选择理想轴线上的一点为(x0,y0,z0);上坐标系中Z轴的方向向量为b(b1,b2,b3),取其上的一点为(x1,y1,z1),可得

(1)

(2)

式中:α为上坐标系原点固定后,Z坐标轴向方向向量a旋转的角度;d为上坐标系中的Z坐标轴在旋转过程中过原点且垂直相交于理想轴线方向所移动的距离。

下侧激光传感器原理同式(1)、式(2),取下坐标系的方向向量为c(c1,c2,c3),旋转角度为β,移动距离为g。

将下坐标系采集的位置数据取反,即通过下坐标系Z轴旋转其XOY平面至上坐标系,与上坐标系理想轴线的方向向量同向。假设下理想轴线在下坐标系的方向向量为c(c1,c2,c3),下理想轴线在下坐标轴中相反的方向向量为h(h1,h2,h3),计算出下侧激光传感器测量坐标系需旋转的角度θ为

(3)

通过对两侧采集到的陶瓷基板位置数据进行平移与旋转,将上坐标系的位置数据向方向向量a反向旋转α角度,向过原点且垂直相交于理想轴线的相反方向平移距离d;下坐标系的位置数据向方向向量c反向旋转β,向过原点且垂直相交于理想轴线的相反方向平移距离g;进一步的,通过对下坐标系的位置数据取反,再绕下坐标系的Z坐标轴反相旋转θ。至此,下坐标系的位置数据转至上坐标系中,通过最小二乘法拟合出上、下两条理想轴线,进一步拟合出公共基准轴线。通过计算上、下理想轴线两端点到公共基准轴线距离最大值的2倍,即可得到同轴度误差值。

同步方面,传感器控制器最多可以联机8个激光传感器,采用与电子计算机(computer of processing,PC)、PLC的无协议指令通信,可进行测量数据的输出及控制的输入输出,保证双激光传感器的同步性,保障测量结果的稳定性。

激光测量模组采用差分测厚法获得厚度数据[11]。双激光差分测厚原理如图3所示,将两组激光传感器同轴固定安装,两激光测头间的距离为D,再测量出两个激光传感器各自到被测表面的距离分别为X1和X2,即可计算出被测物体的厚度dth,其计算公式为

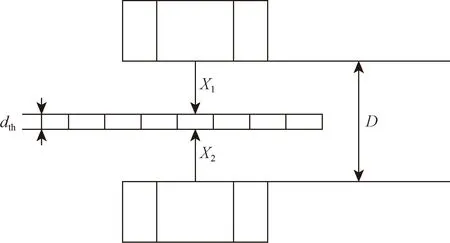
图3 双激光差分测厚原理Fig.3 Principle of double laser differential thickness measurement

dth=D-(X1+X2)

(4)

激光传感器作为整个测厚系统核心的功能部件,担负数据采集的作用,系统精度与其测量精度息息相关[12]。选取的基恩士彩色激光(color laser,CL)系列激光同轴位移计,其内置彩色光源,可进行大范围高精度的距离测量,对应陶瓷材质也具备较高的测量精度和稳定性,基于激光相位测距原理,可以快速精准地测量出到被测表面的距离。

相位激光传感器的测距原理如图4所示,通过对光束进行调制,对被测目标发射激光束,采集测量工件反射回来光的波长,解析出测量相位差,进而得到测量时间,计算出测量点到被测目标的距离[13]。

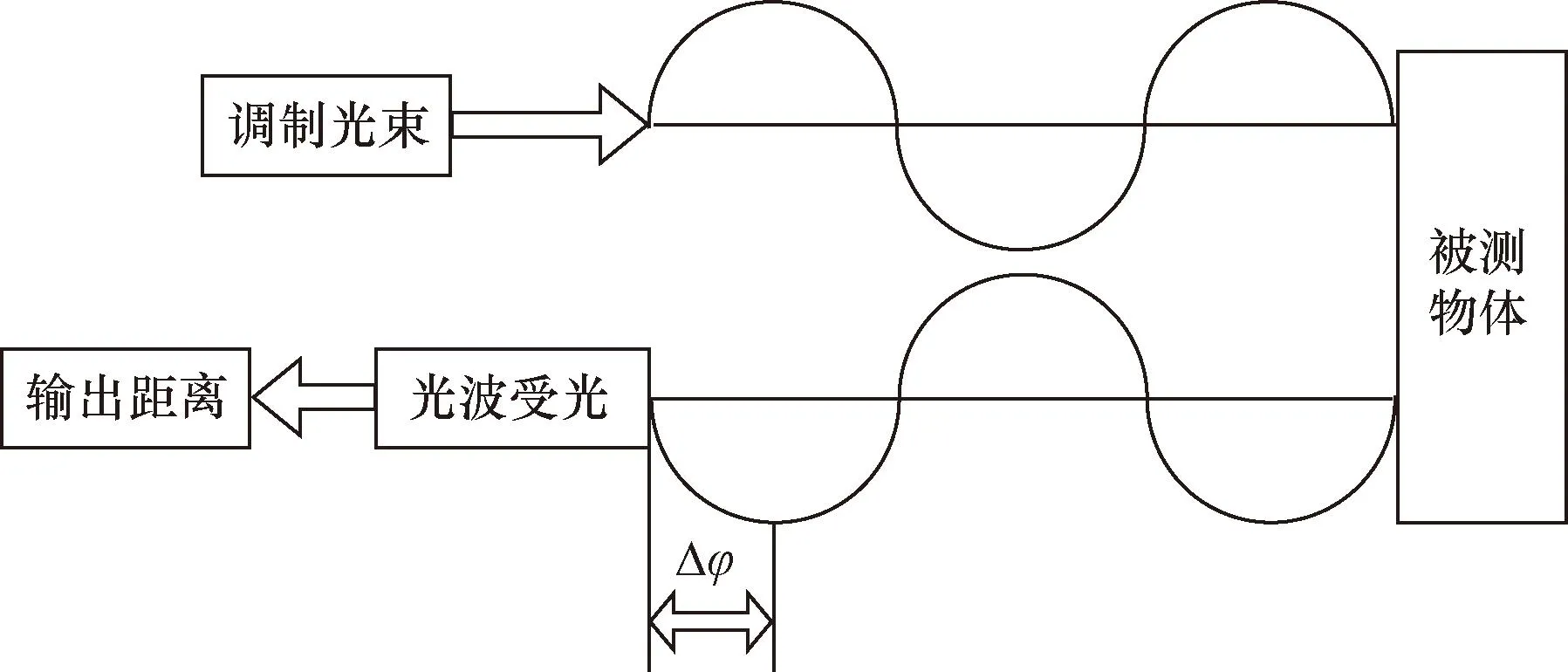
Δφ为不足整数周期的余数相位值图4 激光相位测距原理Fig.4 Principle of laser phase ranging

设调制频率为fV,激光往返一次的时间为ti可以通过调制波的周期数来表达,即

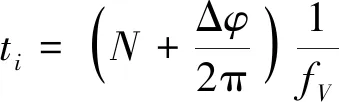
(5)

式(5)中:fV为调制频率,Hz;N为光波往返一次的整数周期个数;Δφ为不足整数周期的余数相位值。

得到时间ti后即可通过光速c计算出被测物的距离,即

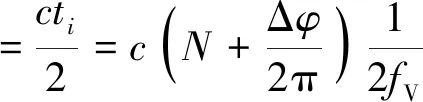
(6)

式(6)中:Xi为测量点到被测目标的距离。

1.3 机械定位模组

机械定位模组负责移动定位治具上的定位点到传感器测量点。定位治具中心处安置有定制的不锈钢镂空扫描架,其镂空处对应陶瓷基板的测量点。将陶瓷基板放入定位治具中后,在四角可安置L型定位块,避免陶瓷基板在镂空扫描架运动过程中发生轻微位移,造成精度误差。

提供动力的XY运动模块藉由两组单轴定位平台堆叠组合,构成龙门架构定位平台,XY模组的行程都是250 mm,依靠滚珠丝杠在导轨内滑动,可以通过X、Y方向运动模组实现陶瓷生片任意点的测量,机械定位模组结构如图5所示。

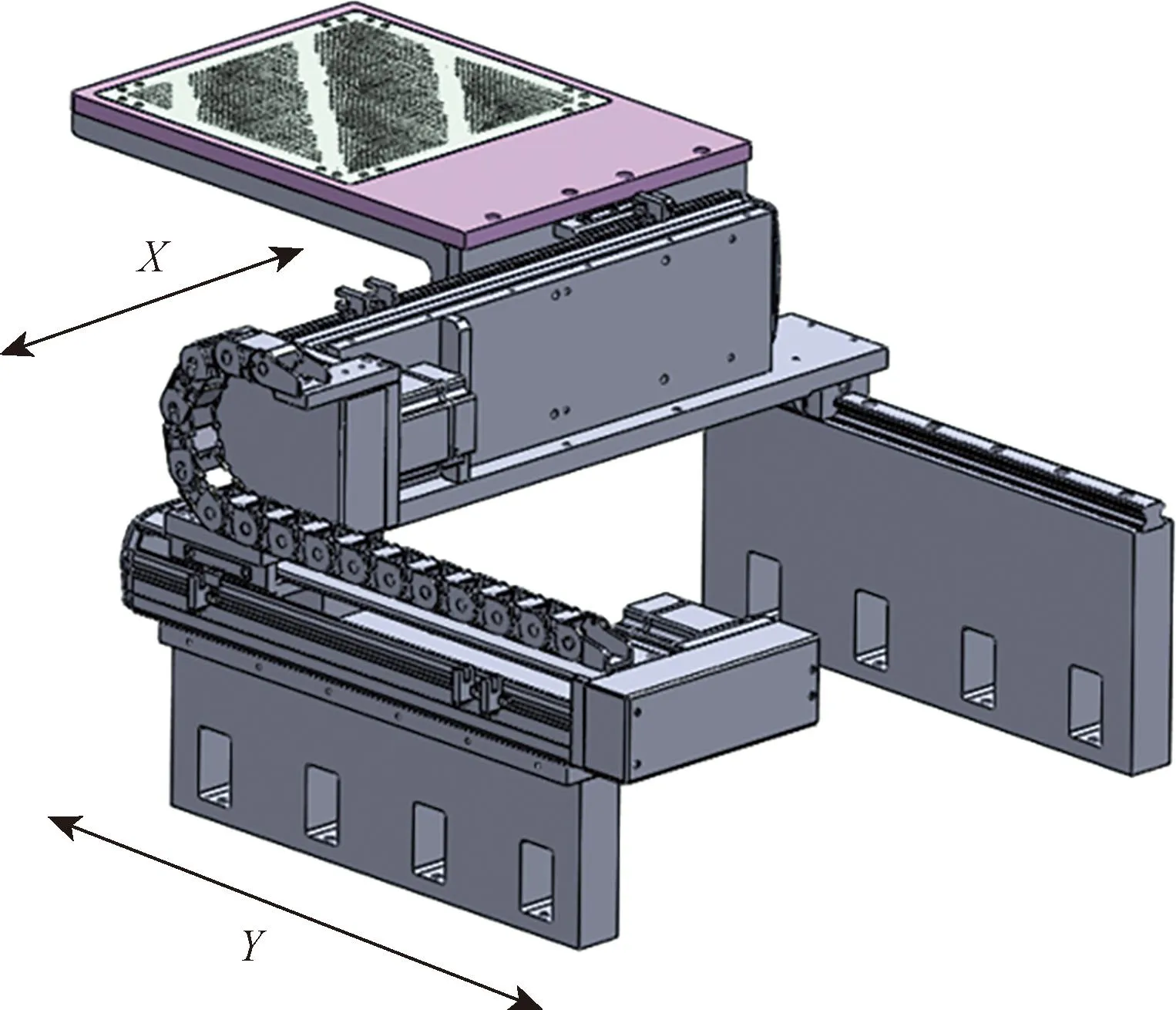
图5 机械定位模组结构图Fig.5 Structural drawing of mechanical positioning module

2 现场实验与误差分析

陶瓷基板的测量厚度在0.6～12 mm,要求测量精度≤ 5 μm,单日测量250片×2次,基于上述要求进行现场测试实验,在实际测试中发现有以下问题:①仪器存在线性误差,测量不同厚度的同材质目标,误差有明显波动;②仪器的稳定性差,随着时间推移,对于同一目标的测量结果也随之变化,误差会逐渐变大。为实现精度要求,针对这些问题,通过数据分析对不同来源的误差进行补偿是常见方法之一。

从功能上分析,系统是由激光测量模组和机械定位模组相互配合,共同完成被测物体的厚度数据采集,因此对双激光测头的性能和机械结构的运动参数进行测试分析,找出误差的主要来源。

2.1 激光测量模组误差分析

2.1.1 静态线性度误差分析

激光测量模组的非线性度是精度误差的主要来源之一,通过开发的系统对激光双测头进行线性度检测。将激光双测头安装在厚度测量用调整夹具上,在测量点固定厚度为1 mm的标准量块,调整两个测头到量块的距离相等,调整两侧的激光测头向量块等间距移动,分别记录下每次移动采集到的数据。在推荐测量范围(70±10) mm内,激光双测头的测量值如图6所示。

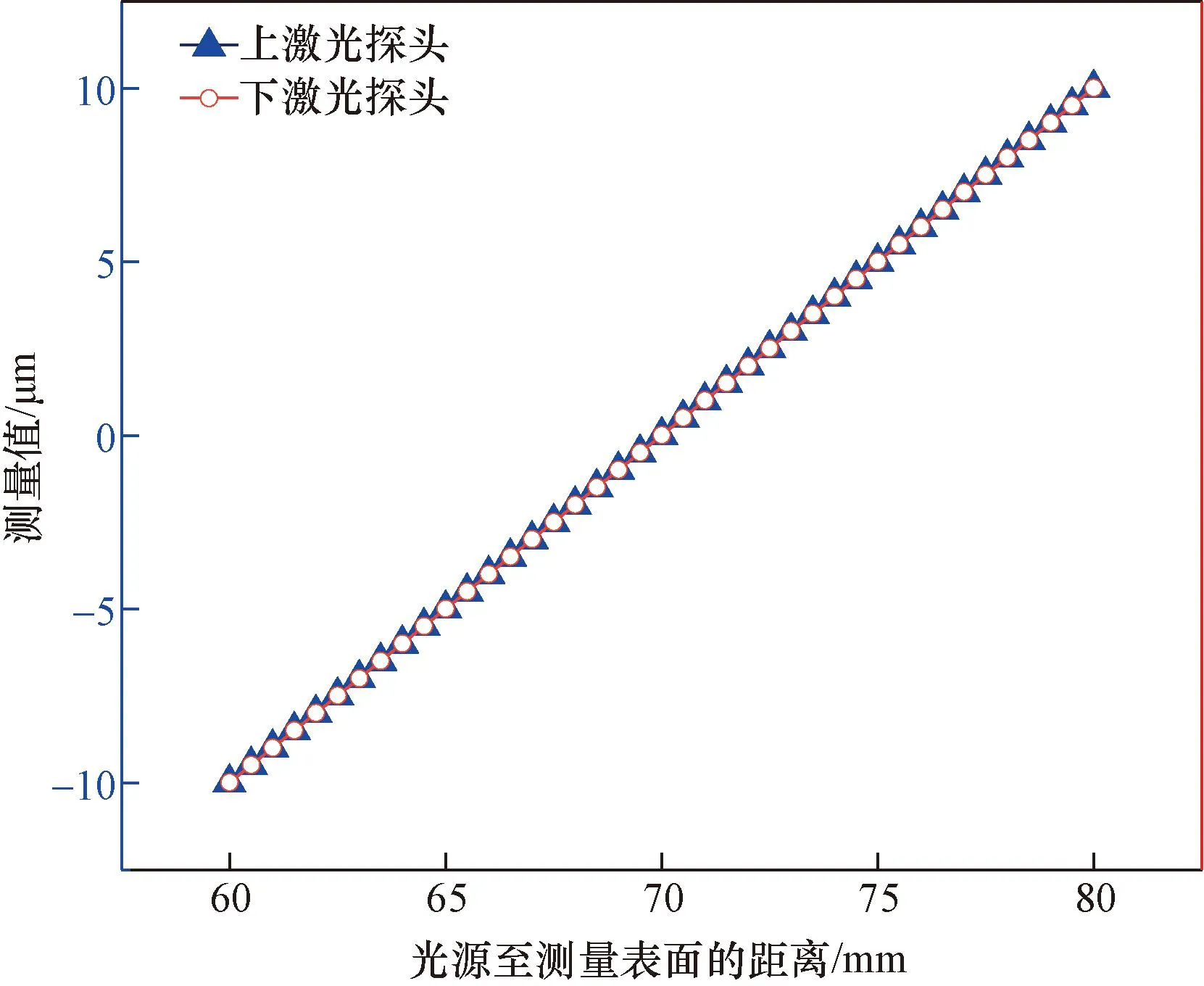
图6 双激光测头输出特性曲线Fig.6 Output characteristic curve of dual laser probe

通过最小二乘法拟合得出上、下测头的输出特性曲线分别为

y1=1.000 1x-70.002

(7)

y2=1.000 2x-70.003

(8)

式中:x为激光测头到测量表面的距离;y1、y2为各自的测量误差,其非线性误差曲线如图7所示。

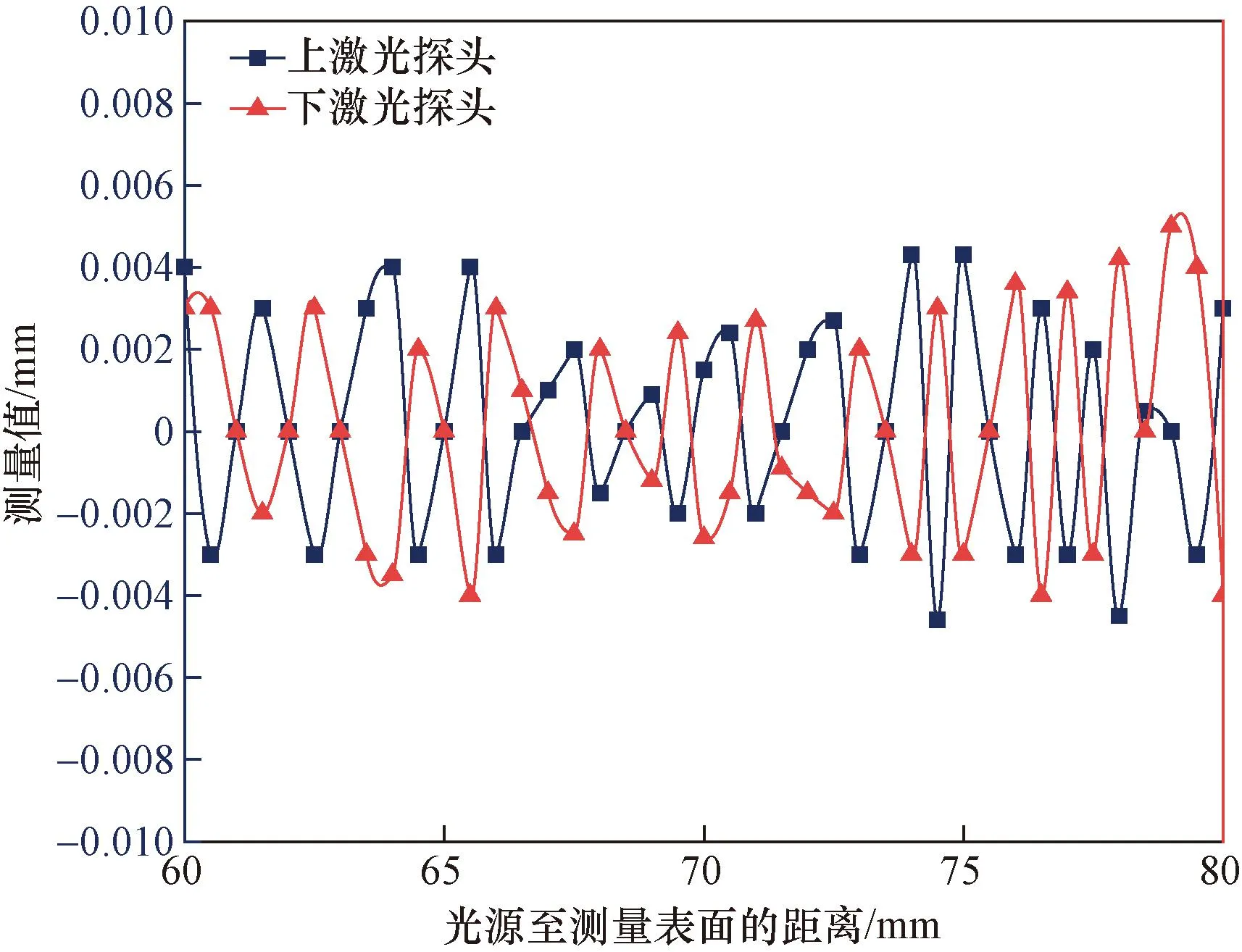
图7 双激光测头非线性误差曲线Fig.7 Nonlinear error curve of dual laser probe

从图7中可以看出,在测量距离70 mm附近的测量误差最小,考虑到测量精度要求,尽量使传感器探头到测量面的距离控制在(70±3) mm的最佳测量范围内。因此,在测量不同型号不同厚度的陶瓷基板之前,先通过厚度测量用调整夹具调整探头,配合系统测量数值,保证传感器探头到测量面的距离X1和X2尽量相等且在最佳测量范围内。

2.1.2 静态重复性误差分析

系统自身需在工作前进行标定设置,具体步骤为测量两个不同的标准量块厚度,将标准量块的数值设置为初始标定值,与实际测量值对比,拟合成两条特性曲线。基于这两条特性曲线,将测量到的厚度数据做非线性优化,消除实测值与显示值之间的差值,即传感器自身的偏移量,如图8所示。

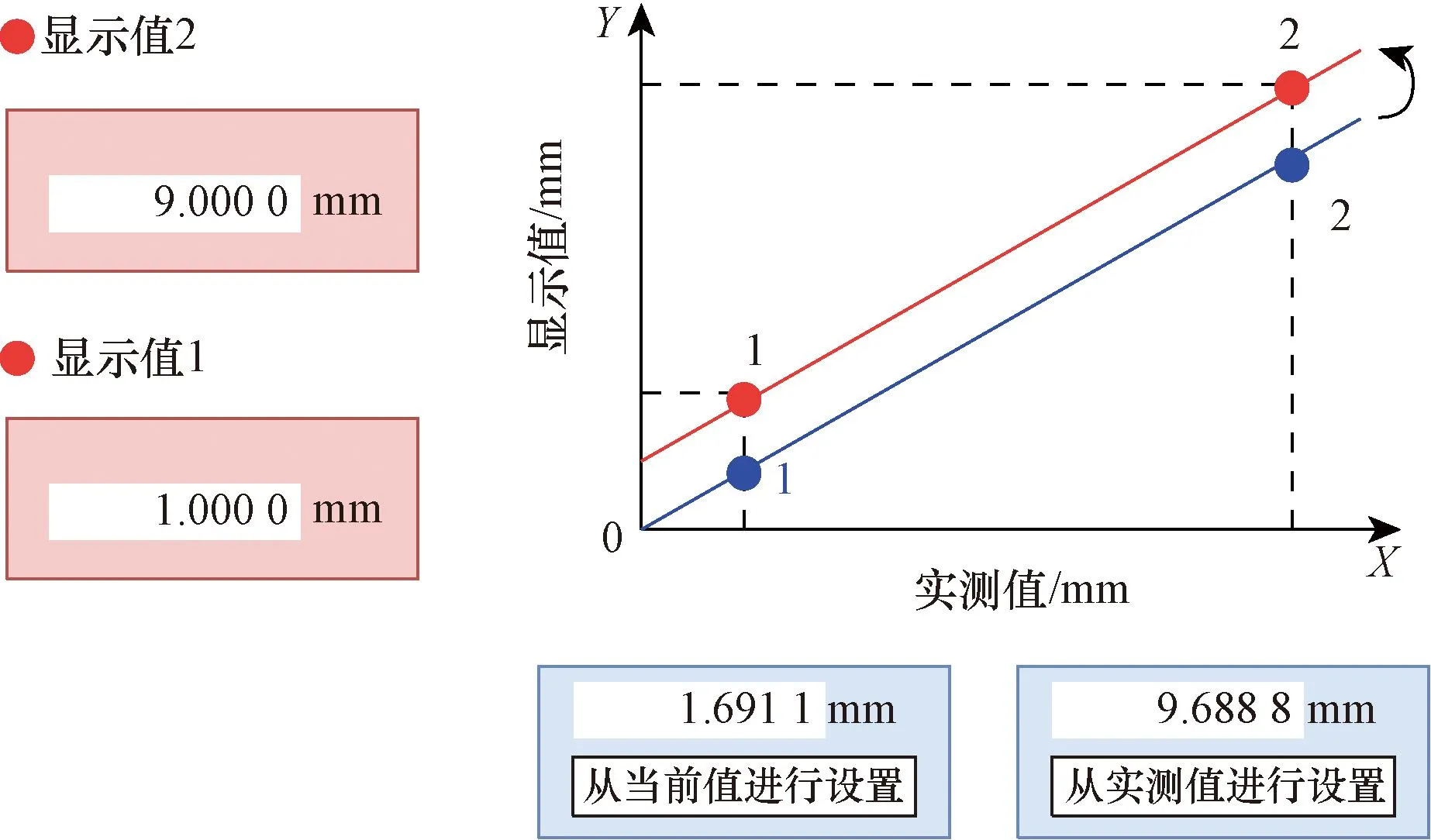
图8 系统标定设置图Fig.8 System calibration setup diagram

通过现场进行重复性实验,在镂空扫描架上固定1.4 mm和1.8 mm的标准量块,设置一个点连续测量600次,做两组,其测量结果如图9所示。

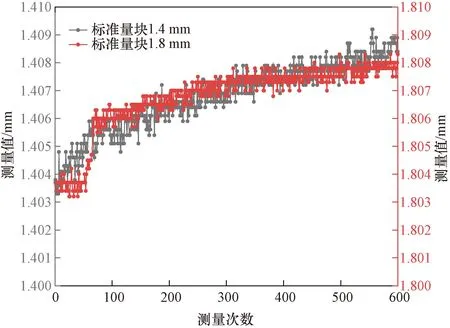
图9 重复性实验误差曲线Fig.9 Repetitive experimental error curve

从图9中可以看出,在激光传感器稳定的静态测量过程中,对同一个点的测量数据,其重复性发生变化,随着时间变化其误差逐渐增大,重复性精度较差。经过程序与数据解析可知:在规定的范围内,当测量值增加和减少时,输出中出现的最大差值,即为滞后值。在长时间的测量过程中,传感器测量的显示值受到温度、光照、暗电流等因素的影响,不断变化,导致滞后值开始变大,进一步致使偏移量逐渐增加,导致系统优化后的结果逐渐偏离实际值,这是构成重复性误差的主要原因[14]。

因此,编写量值溯源调整程序,在系统测量完成一个循环后,根据初始标定值重新开始优化,消除已累计的误差。通过改进后的系统进行同一实验进行数据对比,图10为改进后结果,可以看出,误差的变动趋于平稳,系统重复性显著提高。

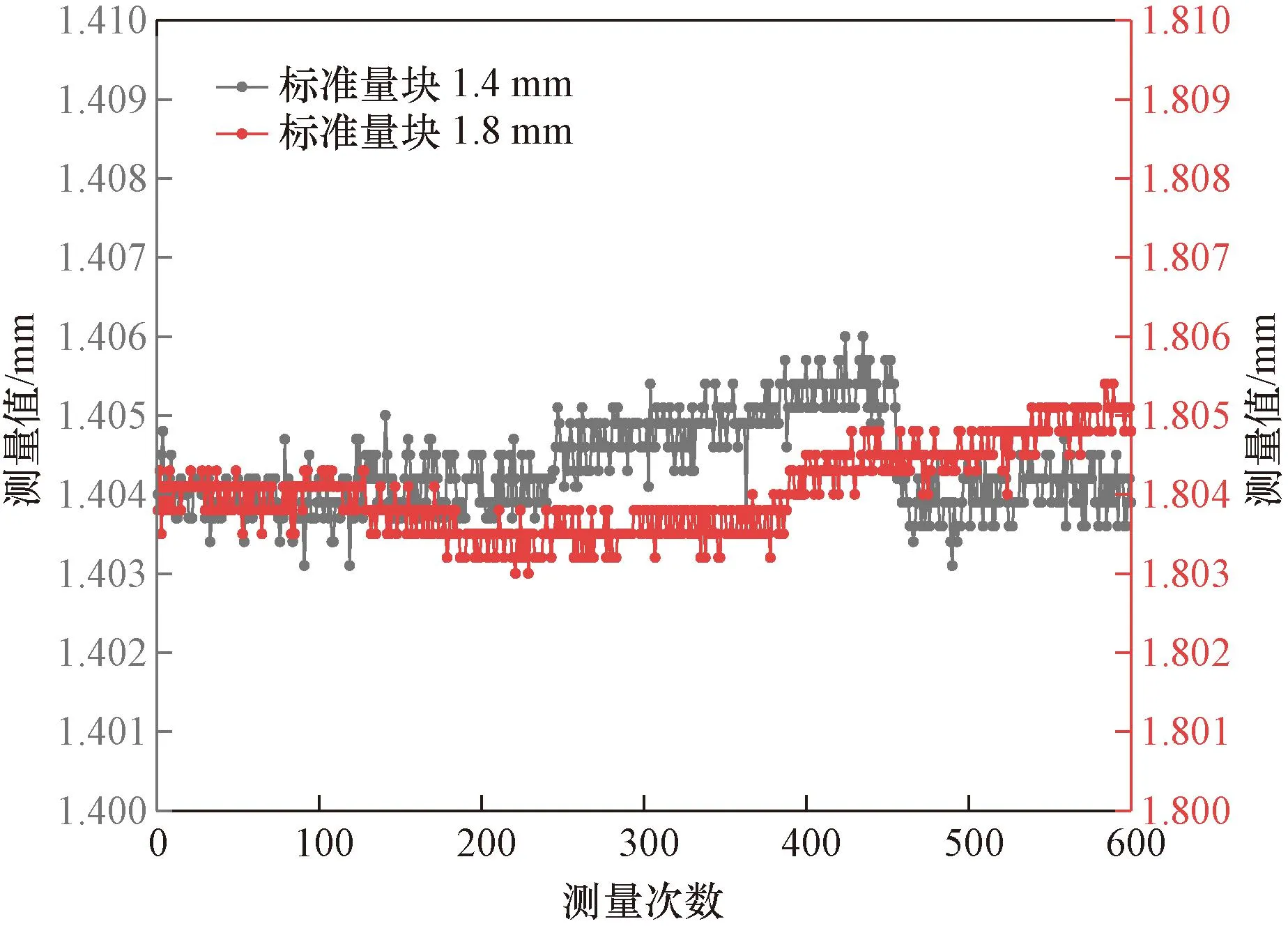
图10 改进后重复性误差曲线Fig.10 Modified repeatability error curve

2.1.3 静态倾角误差分析

理想情况下,双激光测头的激光束应与被测表面相互垂直,但实际测量中,系统自身的机械结构存在加工误差,机械定位模组并非水平,且陶瓷基板为柔性材料,导致传感器的光轴与被测件的测量表面处于非垂直状态,对测量精度造成严重影响。

假设待测件表面的倾角为θ,标准厚度为ds,实际测量的厚度为s,测量示意图如图11所示。

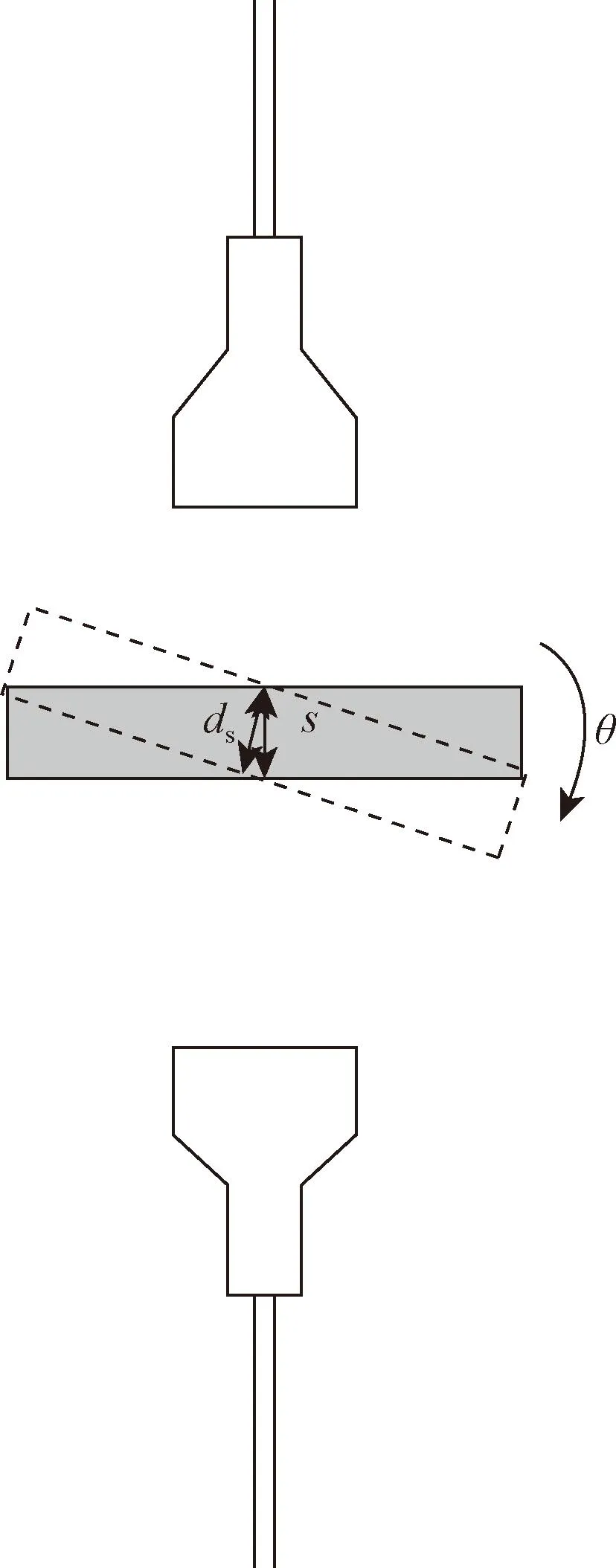
图11 倾角测量示意图Fig.11 Diagram of inclination measurement

由图11可得

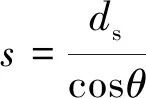
(9)

倾角θ越大,实际测量的厚度数值s就越大,进行倾角实验探究不同倾角引发的测量误差。首先在镂空扫描架上固定1 mm厚度的标准量块作为待测对象,然后通过正弦规分别将测量倾角θ调整为1°、2°、3°、4°、5°、6°、7°和8°,最后记录下激光测量系统采集到的厚度值,分析结果如表1所示。

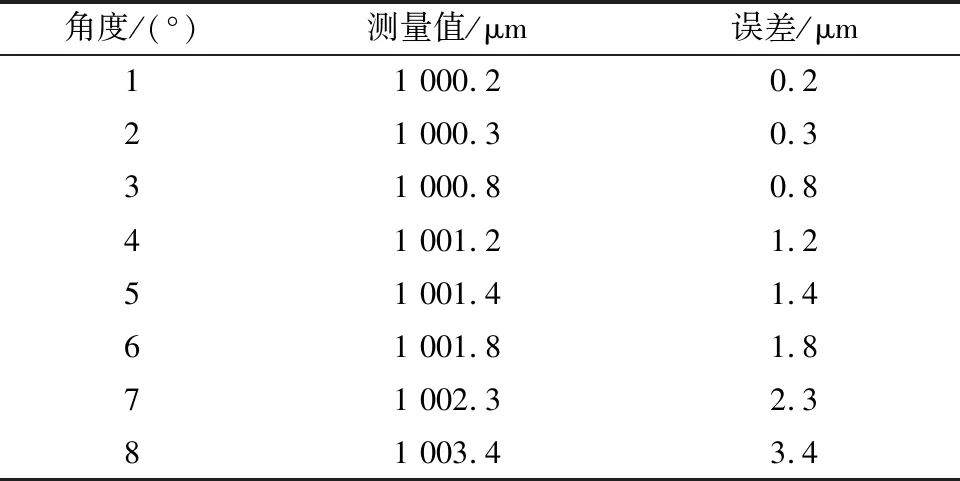
表1 倾角误差分析Table 1 Inclination error analysis

由表1可知,被测面倾角对厚度测量具有影响,误差随倾角的增加而增大,当倾角为7°时测量误差为2.3 μm,综合其他因素的误差影响,已接近系统的精度指标。为了减少倾角带来的影响,进一步改进定位块的结构,在定位的同时将陶瓷生片四角拉伸压紧,将倾角控制在7°以内。

2.2 机械定位模组误差分析

在程序中设置所需测量点的X坐标和Y坐标,通过机械定位模组将定位点的厚度数据采集。在检测多组测量点的过程中,机械运动引起的振动、变形等,都会对测量精度造成一定的影响。经过运动分析,影响测量精度的机械结构相关因素有运动模块的定位精度和机械运动产生的振动。

2.2.1 动态重复性误差分析

运动模块的X、Y两方向单轴定位平台在往复运动中存在定位偏差,工作台所在地面的不平整,自身机械运动及地面存在的振动,都会产生一定的影响,可能导致循环测量时光束的光点逐渐偏离原定点,从而影响测量结果的精度。

通过重复性实验进行分析,固定一块陶瓷基板在定位治具上,设置一个测量点,运动模块在该点和原点之间往复运动,设置循环测量600次,数据分析如图12所示。

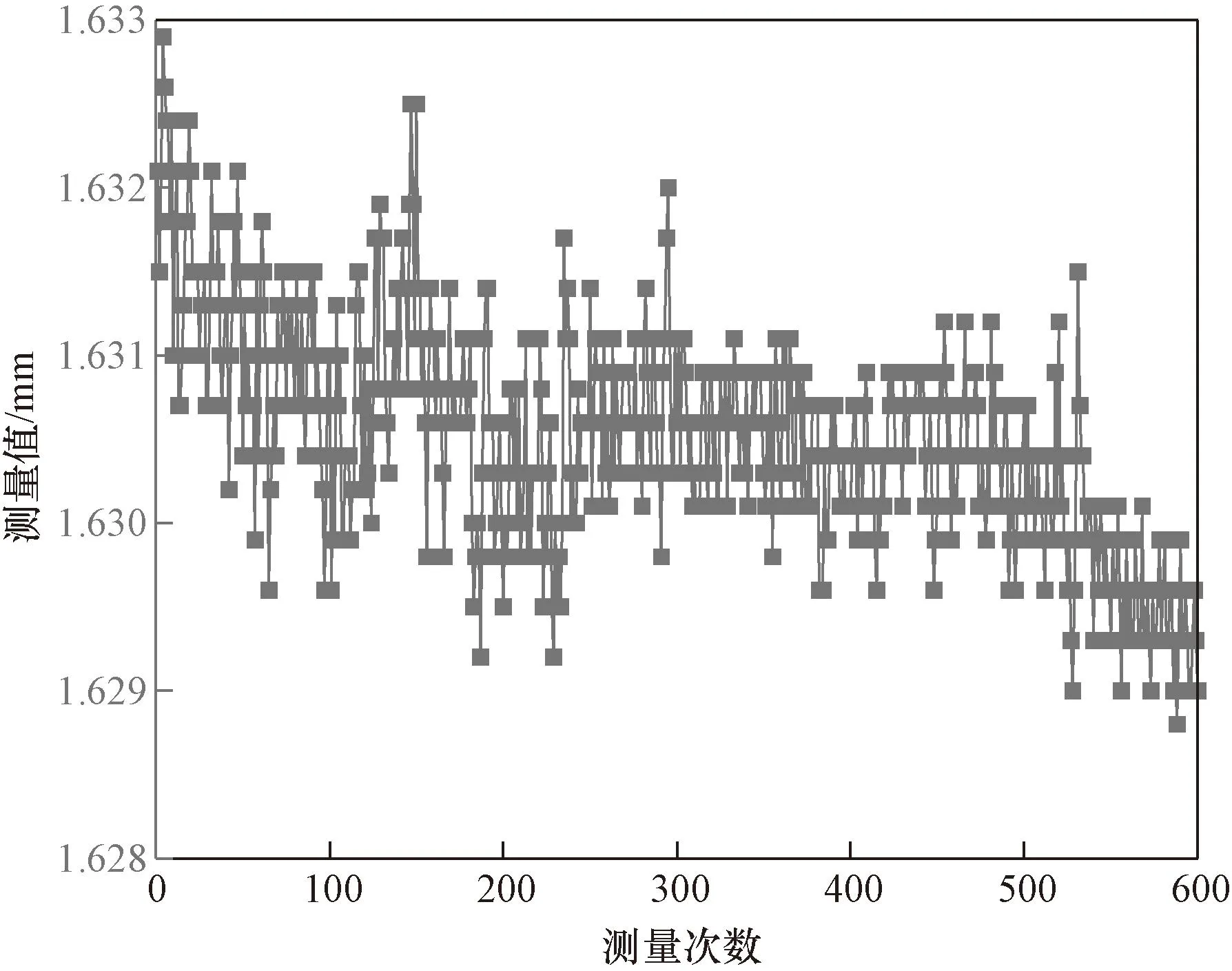
图12 单点循环测量结果Fig.12 Single point cycle measurement results

从图12中可以看出,在600次测量中,厚度波动明显,重复性较差。针对这种情况,在机械结构方面,对于XY运动模块,通过细化设计基准,保障较高的重复精度和定位精度;运动模块直接安装于底座上,自身振动影响较大,在底座与运动模块之间增设一个自水平隔振平台,其防振效果明显,能够保证系统在机械运动过程中的平稳性。在数据处理方面,采取“变异点滤波法”,如果某一个点和相邻两点的数值超过阈值,即为变异点,给予消除。改进后重复实验,数据分析如图13所示,可以看出,厚度数值无较大变化,在1 μm的范围内波动,系统的动态重复精度显著提高。

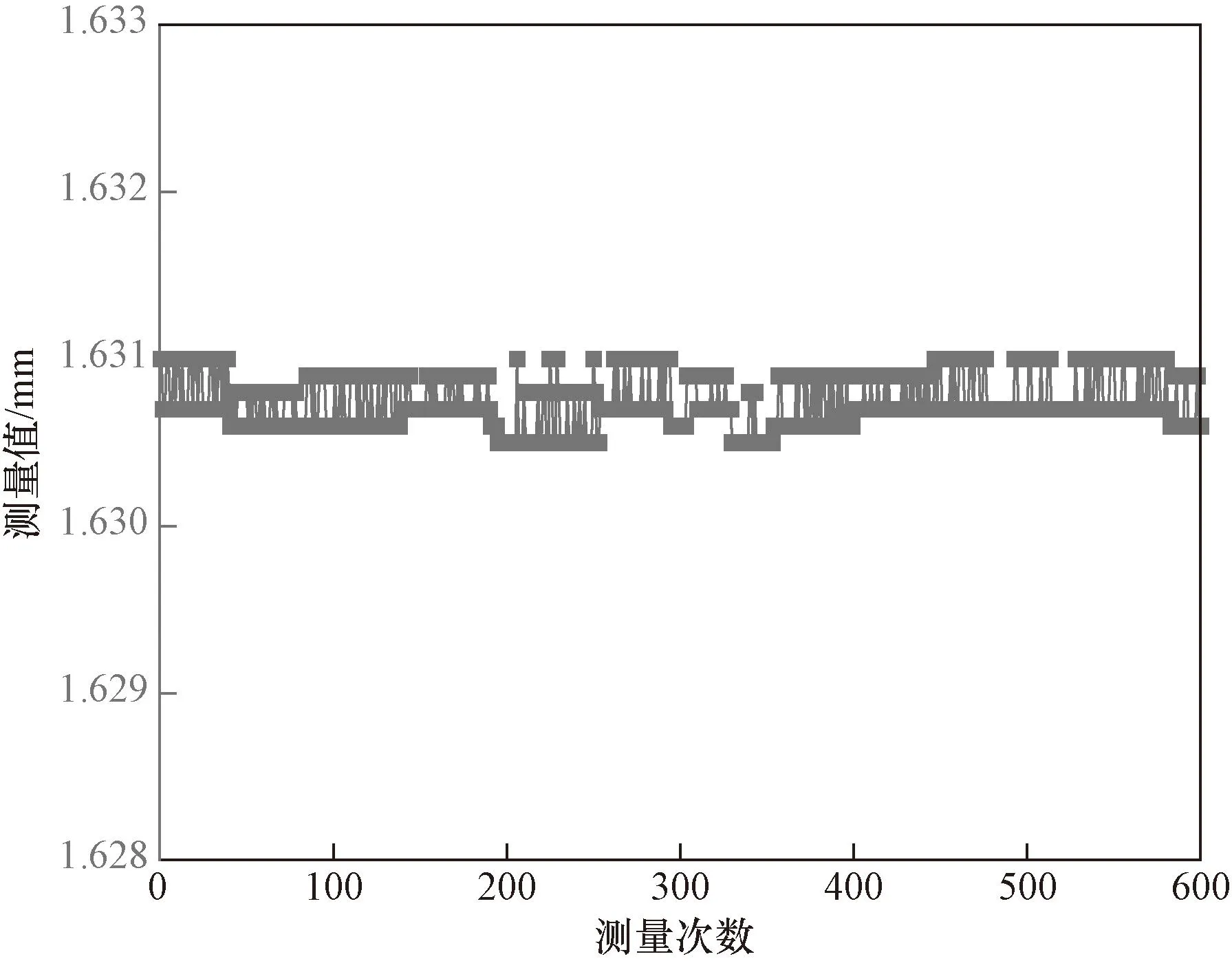
图13 改进后单点循环测量结果Fig.13 Improved single point cycle measurement results

2.2.2 动态机械振动误差实验

静态测量的情况下,两个激光测头的间距D是保存不变的,测量点处的轻微位移不会影响测量结果,这从原理上消除了机械运动带来的一些误差影响。但机械运动会导致两个激光测头的间距D变化,是引发测量误差的可能因素。在半封闭的工作环境中,机械结构的变形很大程度上来源于机械运动,因此需要对系统采集到的厚度数据进行滤波处理,消除机械振动带来的影响。

XY运动模块通过滚珠丝杠连续滑动运行,机械振动的频谱的连续且相似的。在相同的工作条件下,采集不同陶瓷基板的频谱数据,对数据进行傅里叶变换,设置起始频率为fa,终止频率为fb,通过余弦相似度公式进行计算,得出所选频谱的余弦相似度C,其计算公式为

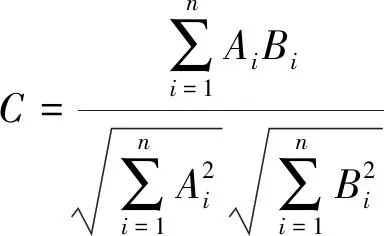
(10)

式(10)中:Ai、Bi为两组频谱区间的采样点;n为带宽,

n=fa-fb

(11)

将所选频谱向右扩展L的距离,起始频率仍是fa,终止频率值变为fb+L,通过上述余弦相似度公式计算扩展后频谱的余弦相似度C1;重复上述步骤m次,比较多次计算结果,选择其中的最大值Cmax,针对Cmax所在的相似区间,设置滤波器对数据进行滤波处理[15]。

为了验证滤波处理后数据的有效性,采用同一批生产的产品进行静态间隔测量和动态连续测量,采集定位点的厚度数据,并用千分尺对比测量数据,测量数据如表2、表3所示。

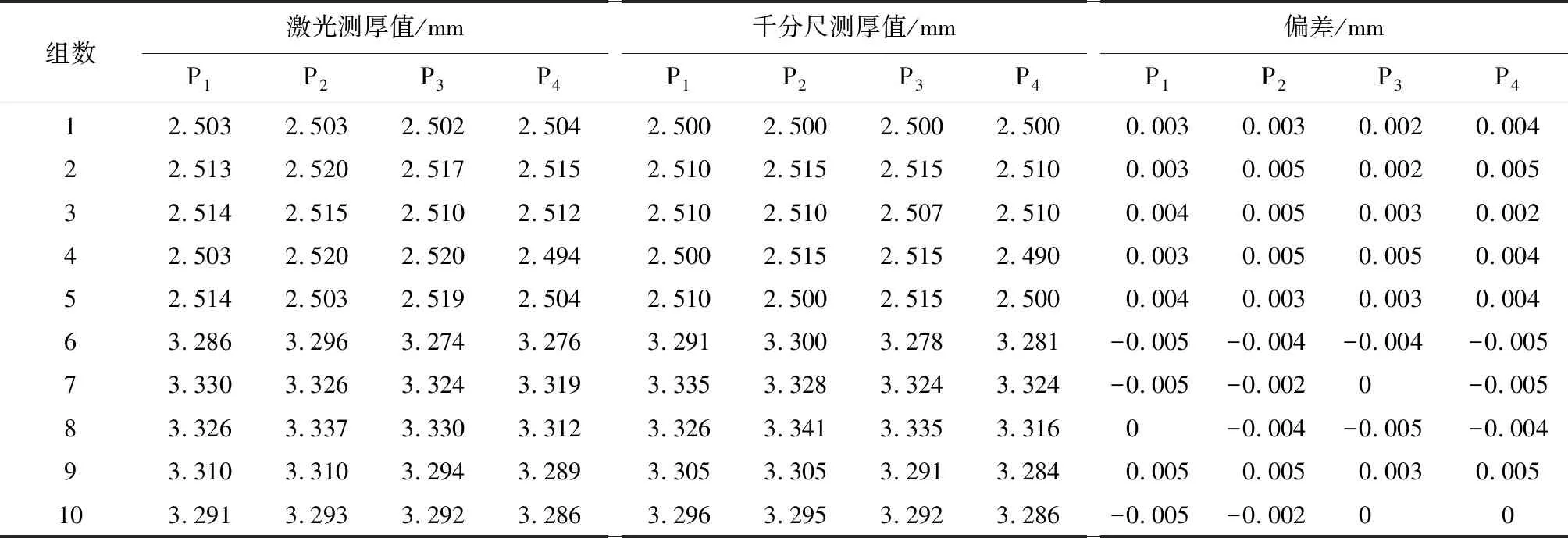
表2 静态间隔测量结果Table 2 Static interval measurement results

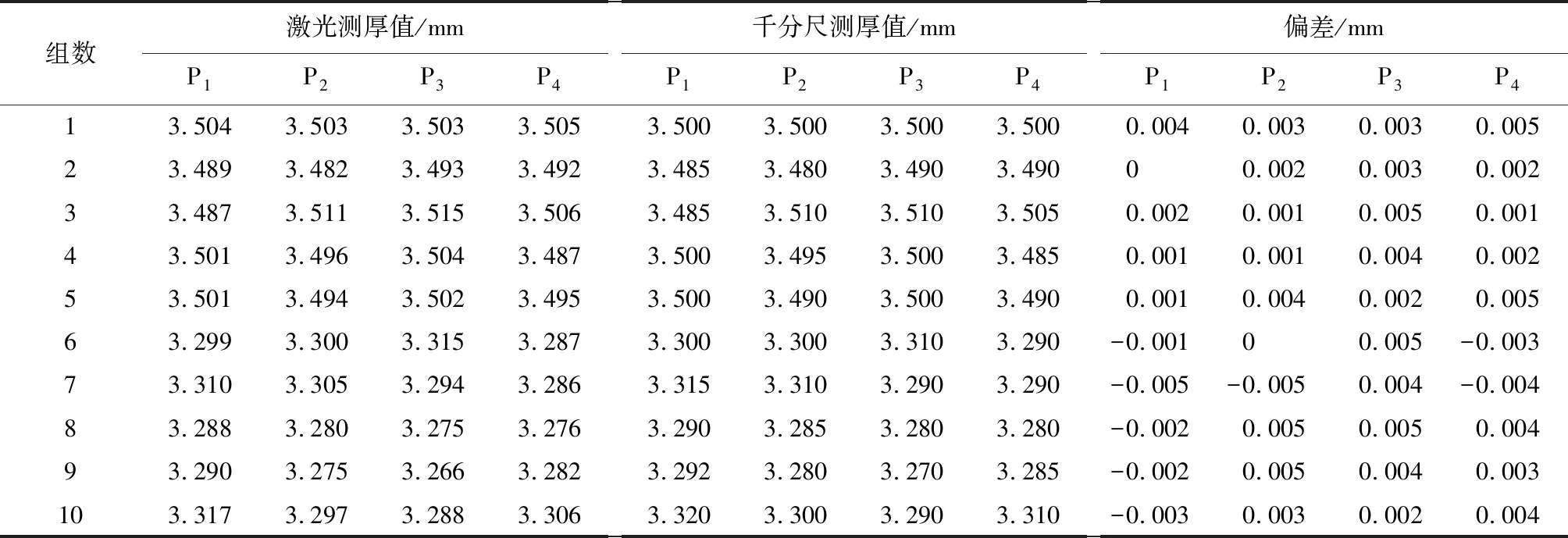
表3 动态连续测量结果Table 3 Dynamic continuous measurement results

系统测量值与千分尺测量值的偏差值如上述表格所示,静态间隔测量和动态连续测量的偏差值整体较为平稳,系统的静态测量精度误差范围与动态测量精度误差范围为±5 μm,两种方式的测量精度大抵相同。实验证明滤波有效去除了机械振动的影响,较好地保留了真实的厚度值,提高了系统的精度。

2.3 结果分析

以一批厚度3.5 mm的LTCC为例,通过精度补偿后的系统测量LTCC,与之前处理过的厚度数据相对比,测量数据的波动明显减小,稳定性明显提高。借助千分尺测量定位点数据,对比结果显示,最大误差为5 μm,平均误差为3 μm,满足测量精度要求。

3 结论

针对LTCC传统测量方式精度不高的问题,设计一种LTCC激光测厚系统。结合产品测量需求,通过现场试验,分析系统的主要误差来源,通过结构优化、标定循环、数据优化、滤波处理等方法,克服了线性度误差、传感器数值误差、机械结构振动误差等因素带来的影响,对系统进行优化改良。结果表明,LTCC激光测厚系统精度误差≤5 μm,达到需求指标,在LTCC的生产领域和薄板测厚领域有广泛应用前景。