具有双重时延的电力信息物理系统的同步控制

宋晴, 李琰*, 葛耀东, 徐天奇

(1.云南民族大学云南省高校电力信息物理融合系统重点实验室, 昆明 650504; 2. 云南省无人自主系统重点实验室, 昆明 650504)

随着先进的通信技术被广泛的应用在现代电力系统中,传统电网逐渐向电力信息物理系统(cyber physical power system, CPPS)靠近。CPPS是由电力网与通信网耦合而成的双层网络,先进的信息系统,如测量系统和管理系统,有助于对电力网的运行状态掌握的更加全面,控制技术也更加有效[1-2]。在电力网同步状态下,所有的节点都运行于同一相位和频率,并且电力网许多环节都需要运行在同步状态下[3]。针对单个电网的同步控制,文献[4]针对弱电网提出了一种机-网侧变流器混合功率同步的双馈机组控制策略。文献[5]对含异构微源孤岛微电网中由于锁相环与电网的耦合作用导致VSG(virtual synchronous generator)失稳的问题,提出基于虚拟电流的VSG预同步控制策略。文献[6]针对光伏并网出现的同步稳定性下降稳定设计逆变器附加H∞阻尼控制进行参数的整定提高了光伏并网的同步稳定性。而在CPPS中,同步是指系统内的节点,在外部驱动或者相互耦合的作用下,调整它们的节点动态行为达到期望的轨迹[7-8],即系统从一个稳定状态,接受指令之后,调整自身的行为,重新达到一个新的稳定状态。在CPPS中时延会使节点接受指令延迟导致相应的动作延迟等状况的发生,会严重影响到系统的同步[9]。大部分时延是由通信容量的限制等原因而产生,所以时延对CPPS同步的影响是一个值得令人关注的问题。

目前关于复杂网络同步与控制的研究已经在单层网络取得很大的突破[10-11]。文献[10]分析了一类具有量化网络攻击的单层复杂网络的自适应事件触发同步控制问题。但是与研究单层网络不同,双层网络的节点数目更多,拓扑结构更复杂,节点类型更加多样,研究其同步的难度也更大[12]。CPPS属于复杂网络的一个特例,节点具有异质性且更复杂,而大多数复杂网络是基于同质节点的理想模型进行分析的[13-14],所以关于单层复杂网络在同步与控制方面的研究成果不能直接应用于CPPS中。由于系统内节点的异质性以及时延或者扰动的存在,使系统仅依靠自身的耦合作用很难同步,所以需要给系统节点施加控制器。为此提出了牵制控制[15-16]、事件触发控制[17-18]、自适应控制[19]和间歇控制[20-21]等控制方案。文献[15]分析了在信息物理系统这类复杂动态系统里基于牵制控制设计了控制方案,但是方案是基于同质节点设计且并未考虑时延带来的影响。文献[20]考虑时延搭建随机不确定时滞网络模型,并且设计了间歇控制器改善时延带来的影响。但是系统仅包含一种时延。由于系统内节点较多,测量节点状态的成本过高,针对这类问题,文献[22]提出对节点的输出反馈量化的同步控制方法,减轻了信息传输带来的压力。文献[23]考虑电力网与通信网的互相影响,基于复杂网络理论提出信息熵的重要节点识别方法,找出电力信息耦合网络的重要节点。分析可知,在CPPS这类双层异质复杂网络中不只有一种类型的时延,所以对于CPPS来说具有双重时延的异质系统模型将更具有一般性,设计的控制器也更加有效。

基于上述讨论,以节点间不同耦合强度系数区分节点类型,考虑节点时延和耦合时延,搭建出具有双重时延的异质CPPS模型。提出自适应同步控制器解决小规模系统中时延带来的影响。考虑大规模系统的复杂性,基于牵制控制设计自适应牵制同步控制器,可以有效减少控制器的数量。自适应牵制同步控制器对解决实际大型系统难控制的问题具有一定的指导意义。

1 系统模型

1.1 电力信息物理系统模型

在CPPS中,电力网与通信网的层间耦合模式为相互依赖模式,电力网主要包括发电机节点与负荷节点,并为通信网运行提供电力支撑;通信网主要为通信节点,负责监测与控制电力网节点。考虑电力网与通信网节点皆为N的CPPS模型为

(1)

令{C1,C2,C3,C4,dX_Y}∈c,则网络模型[式(1)]变化为

(2)

式(2)中:G=(gij)∈R2N×2N为CPPS的外耦合矩阵;Zi为CPPS中节点i的状态;Zj为节点i的所有邻居节点;1≤i≤N为电力网节点;N+1≤i≤2N为通信网节点。

1.2 具有双重时延的电力信息物理系统模型

耦合时延一般在电力或者信息传输的过程中由于节点之间的物理距离较远而产生。考虑到电力网节点是由实际电力网中的电力设备(如变电站、发电厂、开闭所等)高度抽象而成。因为这些电力设备之间的物理距离较远,电压电流波的传输或者断路器动作等等会产生时延。通信网节点也是由实际网络中的通信设备(终端服务器、工业路由器、TCP客户端等)高度抽象而成。并且通信设备由于通信网节点之间的距离或者通信容量等原因会导致通信网节点含有时延。

节点时延是节点内部由于执行器或者控制器对数据的运算或处理等原因所导致。在实际网络中与电力网设备耦合的通信设备需要对电力设备的运行状态实时监测,在运行监测的基础上,对电力网的安全与经济运行实施控制,例如需要监测电力网节点的频率、电压、潮流、发电与负荷容量。所以与电力网节点耦合的通信网节点由于需要收集电力网节点的数据,计算和控制电力网节点运行状态存在节点时延。

将上述两种时延类型同时考虑,可得到同时具有耦合时延和节点时延的双重时延CPPS模型,可表示为

(3)

式(3)中:τ1为耦合时延;τ2为节点时延。

同时含有两种时延的CPPS模型比不含有时延或者单类型时延的模型更具有一般性,它同时包含了节点内部存在或不存在时延、层间或层内节点之间存在时延的各种情况。这表明每一个系统中的节点与其他节点间在传输电力或信息时可能会由于某种原因导致延迟τ时刻后抵达。 那么,在CPPS中如果

(4)

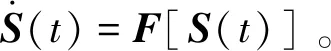
2 自适应同步控制器

因为系统内时延的存在,其同步会受到较大影响,可能会导致系统无法同步或者达到同步的时间过长。为了减小或者消除时延给系统带来的影响,需要添加控制器调整节点的行为。自适应同步控制器主要根据节点输出误差调节控制器增益去调和被控对象以及时延带来的动态变化使定义的误差迅速为零,使系统同步。对于中小型的CPPS,要求其同步速度要快,所以考虑采用自适应同步控制器去控制系统内的所有节点。为了设计自适应同步控制器,首先做以下假设。

假设1对于上述系统模型[式(4)],Z(t)∈Rm,F:Rm×Rm→Rm是一个连续的函数,并且对任意初始值(t0,Z0)都存在唯一的解。

假设2对于向量函数F[Zi(t),Zi(t-τ2)],F[Zi(t-τ1),Zi(t-τ2)],其中,τ1为耦合时延,τ2为节点时延,假定任意的Zi=[zi1(t),zi2(t),…,zim(t)]T∈Rm,S(t)=[s1(t),s2(t),…,sm(t)]T∈Rm都存在L1>0,L2>0,有

‖F[Zi(t)]-F[S(t),S(t-τ2)]‖

≤L1[‖Zi(t)-S(t)‖+‖Zi(t)-S(t-τ2)‖]×

‖F[Zi(t),Zi(t-τ2)]-F[S(t),S(t-τ2)]‖

≤L2[‖Zi(t)-S(t)‖+

‖Zi(t-τ2)-S(t-τ2)‖]

(5)

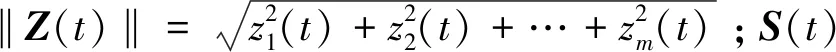
定义系统的误差向量为

Ei(t)=Zi(t)-S(t), 1≤i≤2N

(6)

那么,CPPS的误差系统可表示为

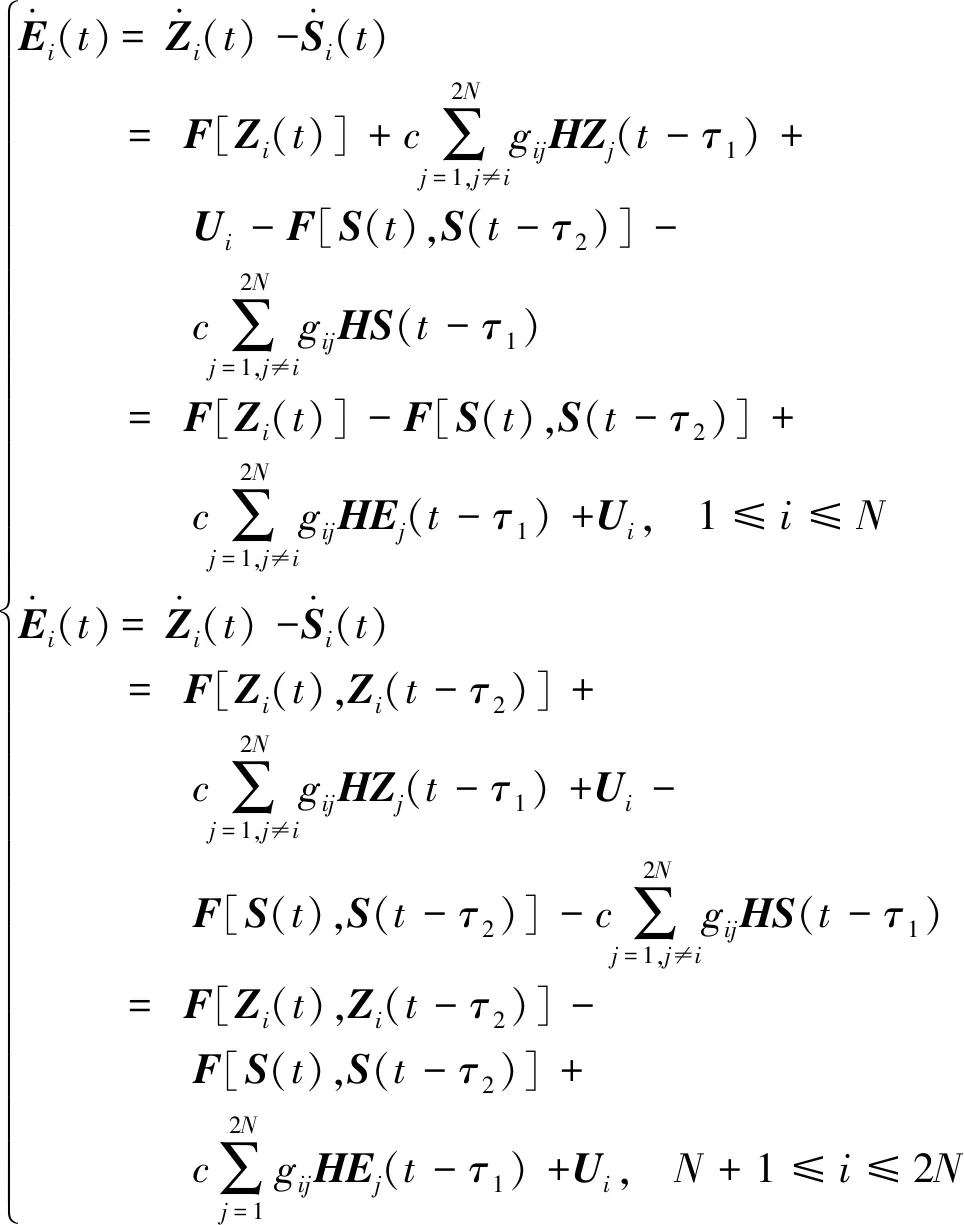
(7)

式(7)中:Ej为节点i的邻居节点的误差。

假定假设1和假设2成立,令自适应同步控制器为

Ui=-kiEi

(8)

式(8)中:ki为控制器的更新律,满足

ki=σi‖Ei(t)‖2exp(μt)

(9)

式(9)中:σi、μ为控制器的参数,是常数。

误差系统可以在控制器的作用下实现收敛,即CPPS系统在控制器的作用下可以达到同步状态。

证明：构造Lyapunov函数,如式(10)所示。

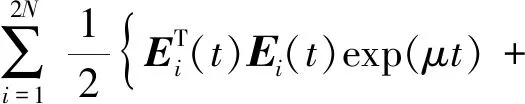
(10)

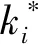
由不等式xTy≤|xTy|≤‖x‖‖y‖,以及式(4)～式(9)得

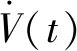
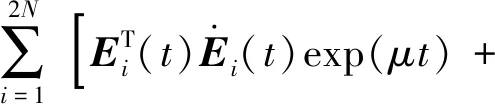
(11)

当1≤i≤N时,满足:

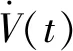
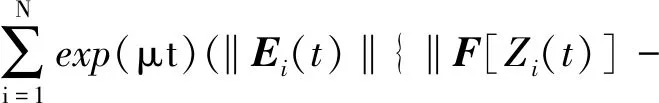
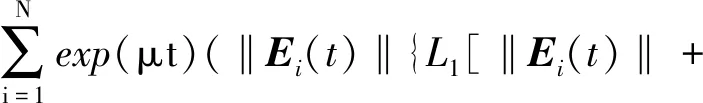
(12)

由2ab≤a2+b2,令L=L1,τ=τ1=τ2,可得

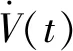
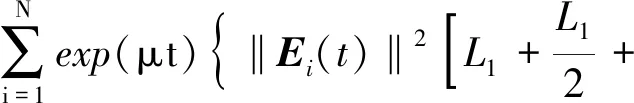
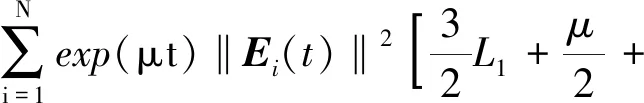
(13)

当N+1≤i≤2N时,类似于1≤i≤N的求解过程,且L=L2,τ=τ1=τ2。因此有

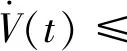
(14)

3 自适应牵制同步控制器

随着CPPS的规模变大,其结构复杂度也会随之提高,系统的全局信息很难被全部掌握,对系统中的每个节点施加控制器的难度也会加大。即使解决困难给每个节点施加控制器,其经济成本也很昂贵,所以需要选取对系统影响力较大的节点进行控制。基于牵制控制的思想可以在系统中筛选出牵制节点集W,对W中的节点施加控制器,其余节点不予控制,其控制器的具体形式表述为

(15)

其误差系统可表示为

(16)

为了判断在牵制节点集的作用下,系统是否可控,介绍引理1进行判断。关于牵制节点集的影响力,以Grounded Laplacian矩阵的最小特征值衡量λ1(2N-l)[24],即系统Laplacian矩阵删除牵制节点集所对应的行和列之后的子矩阵(该子矩阵的阶数为2N-l)的最小特征值。λ1(2N-l)越大说明节点集对系统的影响力越大。

引理1[25]rank(I2N-A,Β)=2N,如果该式成立,则系统在牵制节点集的作用下可以完全可控。其中,A为系统的邻接矩阵,B为控制矩阵,I2N为2N阶的单位矩阵。

在CPPS中,电力网节点的度值越大,说明在实际网络中该节点对电力网的支撑作用越强,影响力也越大,同时该节点对有功功率的平衡、电压与频率的稳定起重要作用;通信网节点的度值越大,说明该节点能够与更多的通信节点进行信息交换,从而影响信息的传输效率。基于节点的度可以算出结构熵,结构熵是利用节点的一阶邻居节点计算出基于某节点的局部网络对整个网络的影响力。节点i的结构熵表示为

(17)

式(17)中:n为节点的邻居节点的个数;j为节点i的邻居节点;Pi为节点i的概率集;Pi(j)的定义为

(18)

式(18)中:degree(j)为节点的度数。

4 算例仿真

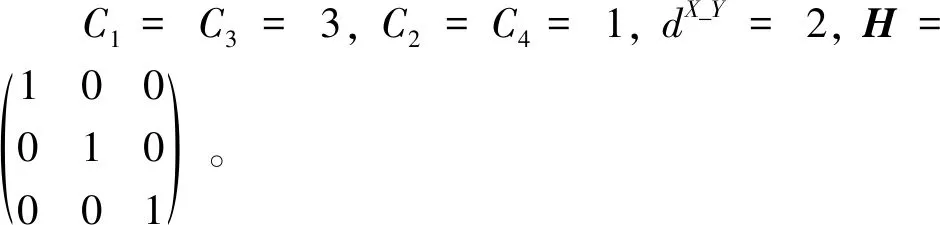
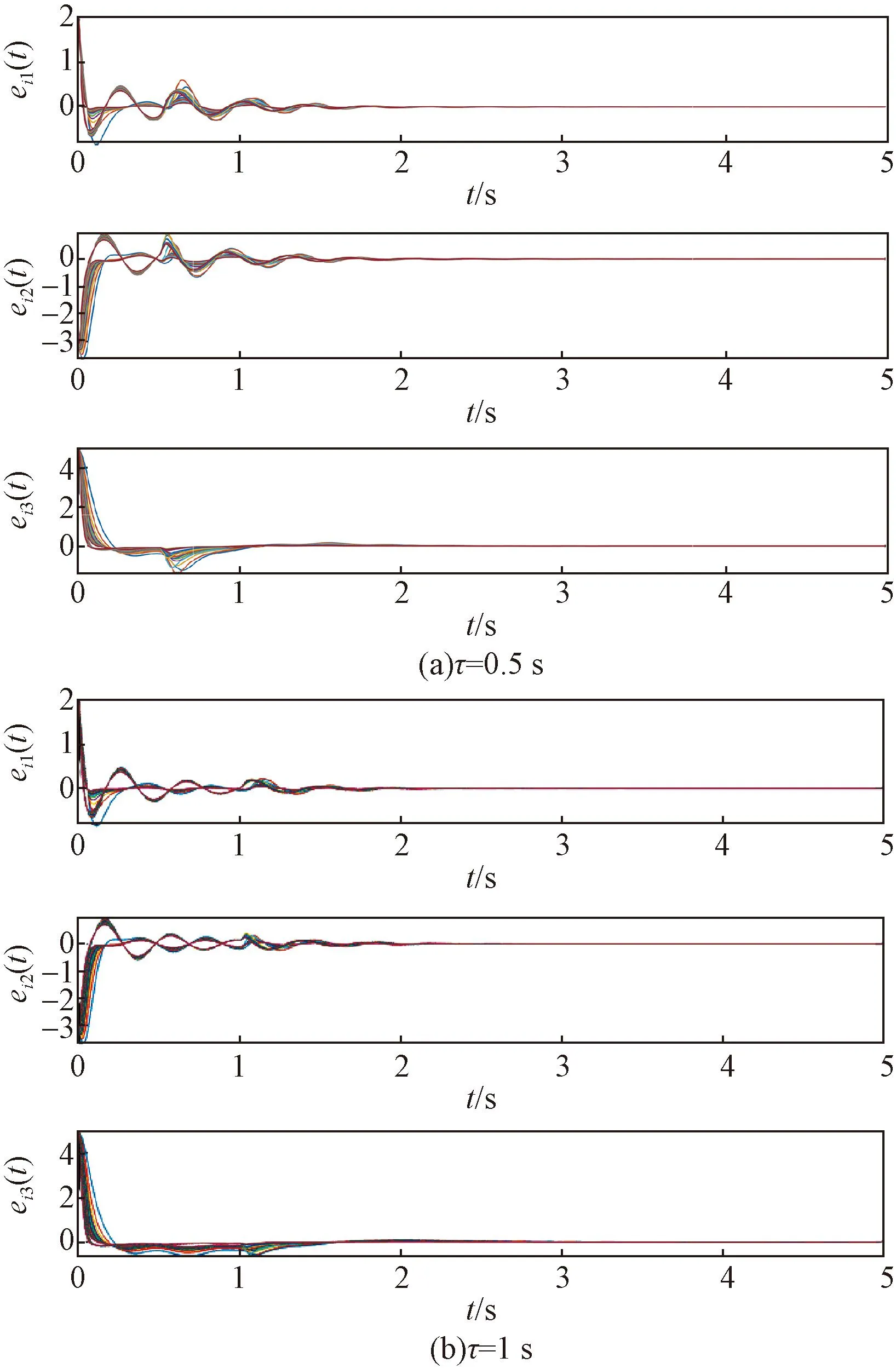
节点i有3个状态分量, ei1、ei2、ei3为3个状态分量的误差变化;τ为时延;t为时间图1 不同时延的系统同步误差Fig.1 System synchronization errors with different delays

考虑电力网为IEEE 118,通信网为118节点小世界网络的大规模CPPS。计算各个节点的度,选取度最高的8个节点如表1所示。

表1 部分节点的度数Table 1 Degree of the partial node

在表1中节点12和节点80的度一致,如果按照度评价节点影响力,那么节点12和节点80对系统的影响是一致的,所以选取牵制节点集W={49,100,12}和W={49,100,80}对系统的影响力也是相等的。

计算出个别节点结构熵如表2所示。在表2中对度相同的节点按照结构熵的大小重新进行了排列,如果按照结构熵评价节点影响力,那么节点80的影响力大于节点12。计算出删除节点或者节点集对应的行和列Grounded Laplacian矩阵的最小特征值λ1(2N-l)如表3所示

表2 部分节点的结构熵Table 2 Structural entropy of some nodes

表3 节点或者节点集的λ1(2N-l)Table 3 λ1(2N-l)of the node or set of nodes

通过表3节点集的Grounded Laplacian矩阵的最小特征值λ1(2N-l)可以看出按照结构熵选择的牵制节点集的影响力要优于按照度选择的。

为了使具有双重时延的系统达到同步状态的时间大约等于理想状态下(不含有时延)系统同步的时间,理想状态下系统部分节点状态分量变化如图2所示。因此,按照结构熵选择牵制节点集W={49,100,80,12,69,201,183,138,145,213}。取c=1,由引理1得rank(I236-G,B)=236,其中,rank表示求秩,G为CPPS的邻接矩阵所以在牵制节点集W的作用下,系统可控。系统的其他参数如上述例子一致。将控制器添加在牵制控制节点集的节点上,图3(a)显示了在小时延的影响下,系统的同步误差可以在规定时间内快速收敛为零。为了更好地消除大时延带来的影响,在之前的牵制节点集的基础上增加了4个控制节点,使W={49,100,80,12,69,201,183,138,145,213,59,168,77,17}。系统的同步误差变化如图3(b)所示。

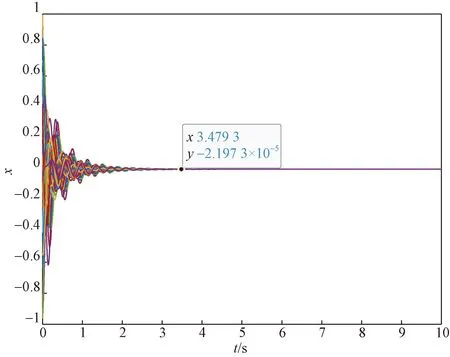
图2 节点(100-136)状态分量变化Fig.2 Node (100-136) state component changes

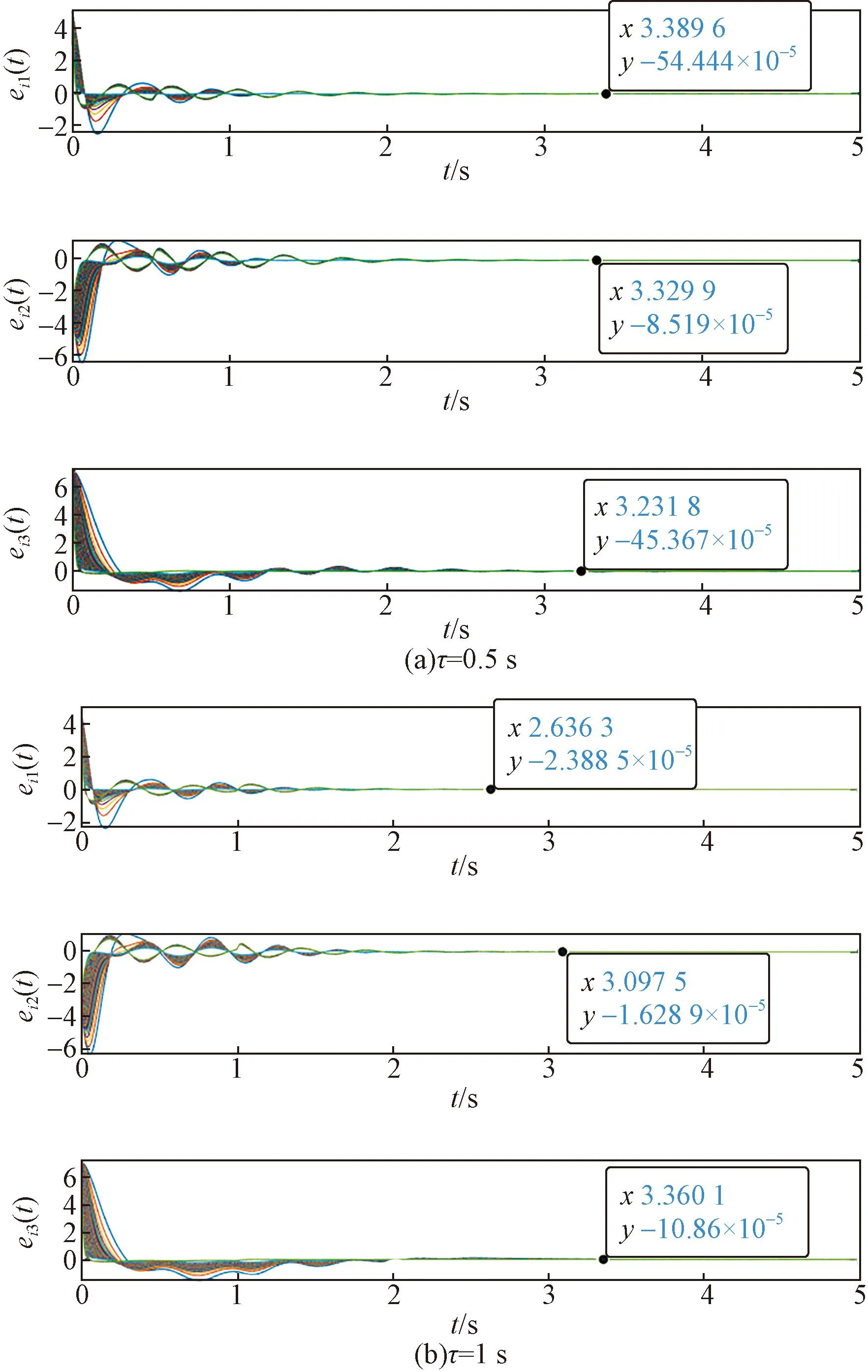
图3 不同时延的系统同步误差Fig.3 System synchronization errors with different delays

5 结论

研究具有双重时延的电力信息物理系统的同步问题,其中时延包括耦合时延和节点时延,在系统模型的搭建中,考虑节点的异质性,并以不同的耦合强度系数表示不同的节点类型。对于时延对系统同步带来的影响,设计了自适应控制器进行处理,并且通过构造Lyapunov函数证明了控制器的有效性。由于大规模系统全局信息难以掌握以及将控制器添加在每个节点上有成本限制,所以基于牵制控制的思想,提出一种适用于大规模系统的自适应牵制控制器。最后,通过两个算例证明两种控制器的有效性。