自制旋转机械故障模拟试验台的转子振动特性研究

王康, 张一凡, 孙天翔, 王永岩, 秦楠

(青岛科技大学机电工程学院, 青岛 266100)

随着科技的进步和经济的发展,现代生产过程对设备的依赖程度越来越高,任何设备都有它的寿命周期,因此设备的故障具有客观必然性。机械设备的迅速发展推动了机械故障诊断技术的不断提升,然而,对故障的诊断研究仅依靠现有故障案例或对理论模型分析是不够的,一套旋转机械故障模拟设备,以便研究人员可随时对所需要的故障类型进行研究分析。旋转机械故障模拟试验台需要模拟不同转速下的各种故障,尤其在模拟点碰摩故障时会使转子受到一定的冲击,不平衡故障会加剧这种情况的发生。在对转子系统进行受力分析的基础上,使用仿真技术手段计算分析,这是研究转子振动特性的常用方法[1]。丛蕊等[2]、程勇等[3]使用数值仿真研究了转子碰摩故障和振动响应。Zhang等[4]建立了转子的运动微分方程,通过仿真和试验对转子的响应进行求解,证明可以调整控制参数改善支承特性。Hajžman等[5]对涡轮转子进行了建模与动力学分析,总结了旋转轴建模的标准方法,并介绍了将基础效应纳入动力模型的两种方法。张永旺等[6]考虑了转子的陀螺效应,创建了基于瑞利梁的转子动力学模型,并用数值仿真进行模态计算。然而,数值仿真中为了追求结果精确而建立的动力学模型往往比较复杂,程序编程也颇具难度。

针对上述情况,有限元仿真可以对转子系统进行静力学分析[7]和动力学分析[8-10],因此有限元软件仿真可以比较彻底的研究转子的振动特性[11]。赵宇等[12]使用有限元软件对整体叶盘进行了仿真分析,并进行了模态分析和振动特性分析。姚星宇等[13]使用ANSYS对转子系统的动力学特性进行了研究,求解出不同预紧力下的临界转速。周涛等[14]为获得转子静力学特性将SolidWorks建立的模型导入ANSYS Workbench进行分析。崔博等[15]针对高速转子的离心应力所致失效问题使用ANSYS Workbench进行了静力学和模态分析。文献[16-19]针对耦合故障建立了转子系统有限元模型,通过仿真得到转速对转子振动特性的影响,并以搭建试验台进行试验来验证仿真结果的正确性。陈付平等[20]、宋骏琛等[21]基于ANSYS Workbench有限元分析软件对转子进行分析,计算了陀螺效应下的临界转速,绘制了转子系统的Campbell图,并与试验结果对比论证。溥江等[22]通过绘制Campbell图来分析转子系统的临界转速、不同转速下的涡动频率,并结合各阶模态振型云图进行分析,为旋转机械故障模拟试验台的设计与结构改进提供了参考。

基于此,以自制旋转机械故障模拟试验台的转子为研究对象,对该系统进行有限元建模和静力学、动力学分析。由于旋转机械故障大多是由转子不平衡引起的,同时碰摩、轴承故障也占部分比例,为确保在故障模拟实验工作转速区间内不会发生共振,提高故障模拟实验的安全性与故障数据信号采集的可靠性,对该试验台转子的振动特性研究显得尤为必要。

1 动态分析理论

通常N自由度有阻尼系统的运动方程为

(1)

而转子动力学分析则必须考虑陀螺效应,它的作用是将转子系统的模态频率的大小与其自转角速度变化生成关系,从而导致转子的径向振动展现为正进动与反进动两类模态[23]。此时动力学方程为

(2)

式(2)中:G为陀螺矩阵;B为旋转阻尼矩阵。

2 转子有限元模型

2.1 建立三维实体模型

研究对象为自制旋转机械故障模拟试验台的转子。该转子由双飞轮与转轴组成,飞轮上设有螺栓孔,可以添加质量块来模拟转子不平衡故障。通过两个深沟球轴承与转子A处、F处轴肩过盈配合,轴承型号为6005ZZ。转子右端由弹性联轴器与三相伺服异步电动机转轴相连,转轴左端与磁粉制动器直接相连。转子结构尺寸如图1所示。

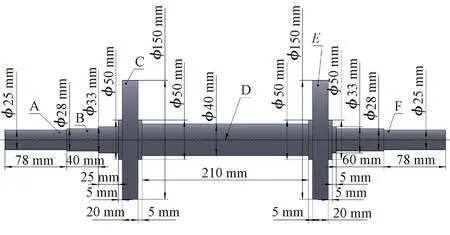
A为轴颈1;B为轴颈2;C为左盘;D为轴中点;E为右盘;F为轴颈3;φ为转轴直径图1 双盘转子结构图Fig.1 Structure diagram of double disc rotor

利用SolidWorks软件对双盘转子进行三维实体建模。在建模过程中,对模型的圆角、倒角、螺纹以及退刀槽等局部特征进行了合理的简化。简化后的模型有利于减少计算用时,提高计算效率,且对计算结果的影响较小。简化后双盘转子的实体模型如图2所示。

图2 双盘转子实体模型Fig.2 Solid model of a two-disc rotor

2.2 建立有限元模型

把SolidWorks生成的.STEP文件导入Altair Hyper Mesh软件进行手动网格划分。根据双盘转子在运动中所表现得结构力学特性,为了提高计算精度,整体采用六面体网格进行划分,对局部轴承接触的网格进行细化处理,并检查了翘曲度5.0、雅可比值0.7等网格质量参数。网格划分后的节点数为16 447,六面体单元数为13 520,得到三维有限元模型如图3所示。

图3 双盘转子网格模型Fig.3 Double-disc rotor mesh model

2.3 材料属性与约束条件

把Altair Hyper Mesh生成的.inp文件通过外部模型组件导入Workbench软件。转轴、飞轮材料均为28MnCr5,输入参数:密度为7 800 kg/m3、弹性模量为215 GPa、泊松比为0.3。

对于转轴类零件的边界条件约束,有多种方法:远程位移(remote displacement):可引入转动自由度,对位移和角度同时设定的约束。圆柱形支撑(cylindrical support):施加在圆柱面可以对径向、轴向、切向单独控制的约束。仅压缩支撑(compression only support):在表面上施加仅限制法向方向移动的约束。

这些方法各有优劣,需要根据情况去选择约束类型。

3 双盘转子静力学分析

分析中使用Compression Only Support作为约束条件,可以更接近于实际情况。以分量的形式在轴颈A、F处的外圆表面上施加Y轴负方向800 N的轴承载荷。打开弱弹簧功能以防止刚体约束不足。为了模拟碰摩力,以分量的形式在碰摩区B处施加Z轴正方向40 N、Y轴正方向8 N的力,材料摩擦系数为0.2,满足库仑定律。对有限元模型求解,得到转子的总变形与Von-Mises等效应力云图如图4所示。

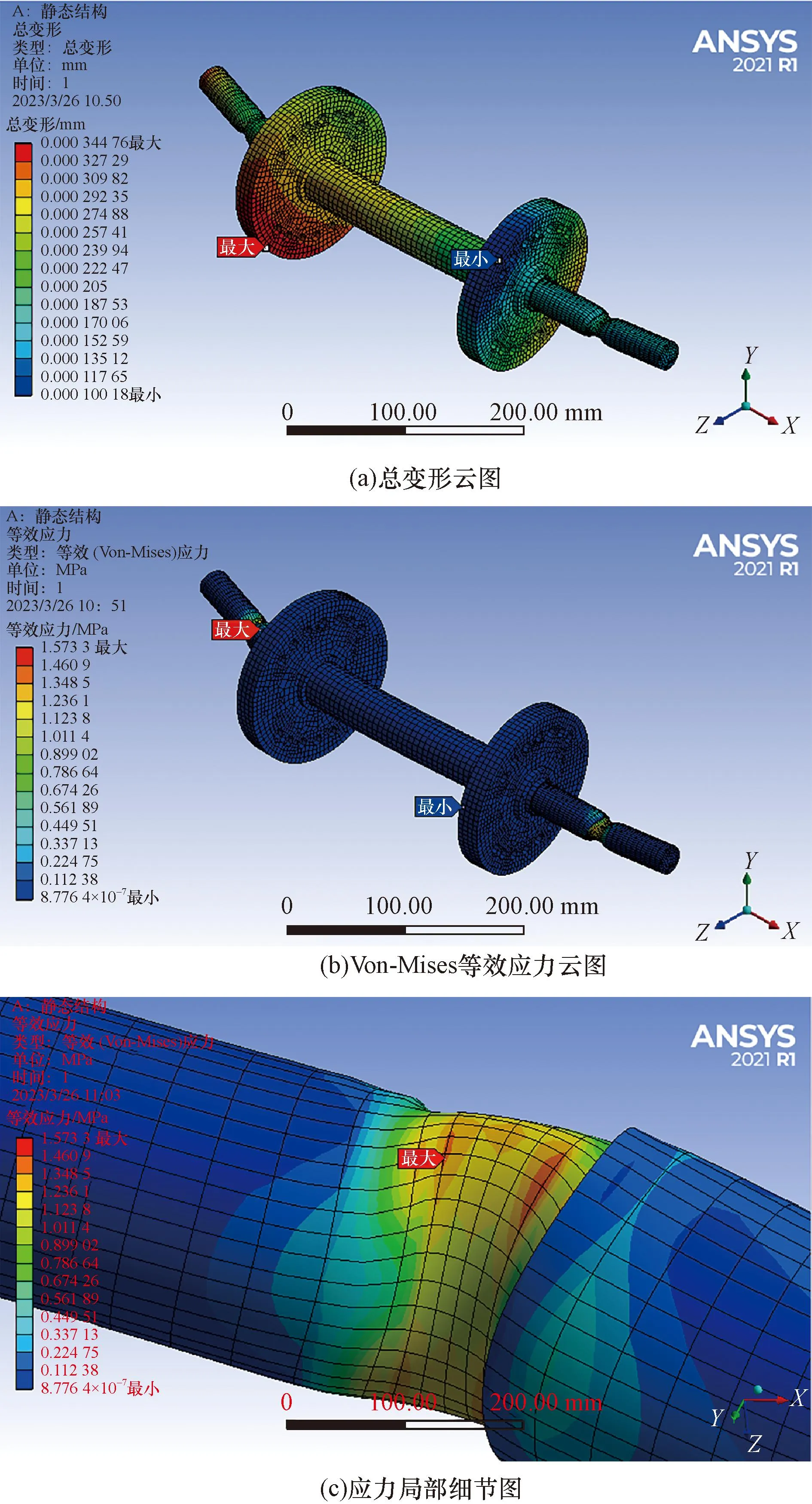
图4 静力学分析云图Fig.4 Static analysis cloud

由总变形云图[图4(a)]可知,最大变形量为0.34 μm,最大值点在近碰摩力飞轮C圆周处。由Von-Mises等效应力云图[图4(b)]可知,最大值点在近碰摩力轴颈A处,最大应力为1.57 MPa。

由应力局部细节图[图4(c)]可以清晰看出,轴承内圈对转轴轴肩的应力情况,由于受到轴承载荷与碰摩力的影响,转轴受到的轴承内圈约束后的局部应力特征应,出现了应力集中。

4 双盘转子动态分析

对于旋转机械故障模拟试验台的转子,通常在模拟故障实验时,受到作用在转子本体上以动载荷形式出现的激振力,而且在模拟多种故障实验中,根据不同情况,转子转速一般能达到高转速带。为了确保旋转机械故障模拟试验台的使用安全性与故障数据可靠性,不仅要对结构进行静力学分析,更要考虑结构的动态特性,当结构在遭受一定幅值的周期性激振力时,可以有良好的动态特性。

因此,对双盘转子模型进行动力学仿真分析,其中包括模态分析与谐响应分析,据此研究该模型的动态特性,并为旋转机械故障的模拟实验提供了参考。对于转子的动力学仿真,还必须重视陀螺效应的影响,同时也应考虑支承条件的设定,以达到准确获得转子振动特性的目的[24]。

4.1 模态分析结果

通过Workbench的模态分析系统对双盘转子进行模态分析,得到转子系统前8阶模态振型如图5所示。

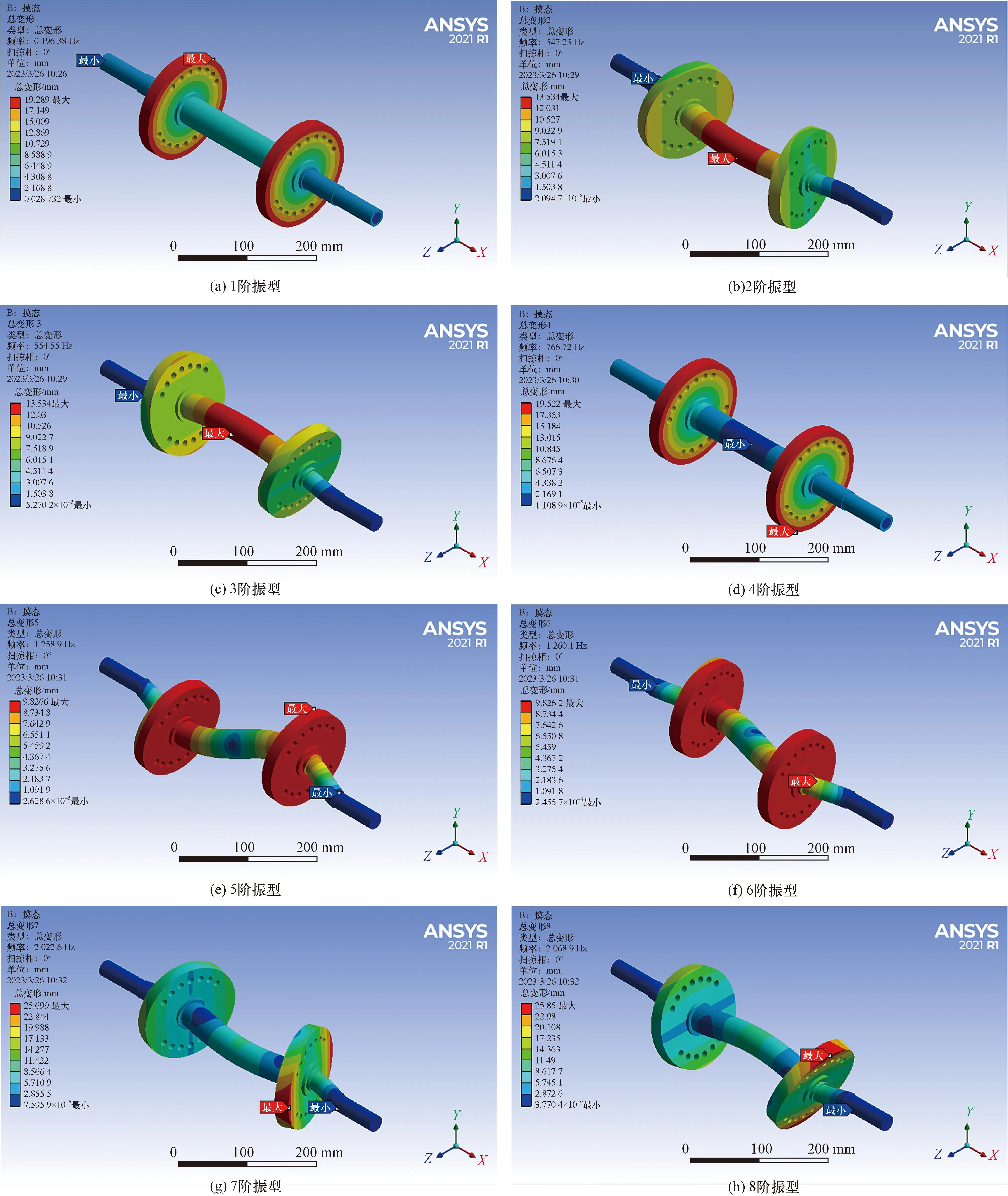
图5 转子系统模态振型图Fig.5 Rotor system modal mode diagram

从各模态总变形的动画可以看出,双盘转子的第一阶振型为刚体模态振型,不予考虑。一阶模态最大位移在转子跨中D处,二阶模态最大位移在左右飞轮C、E处。

固有频率是双盘转子动态性能的重要参数,具体如表1所示。

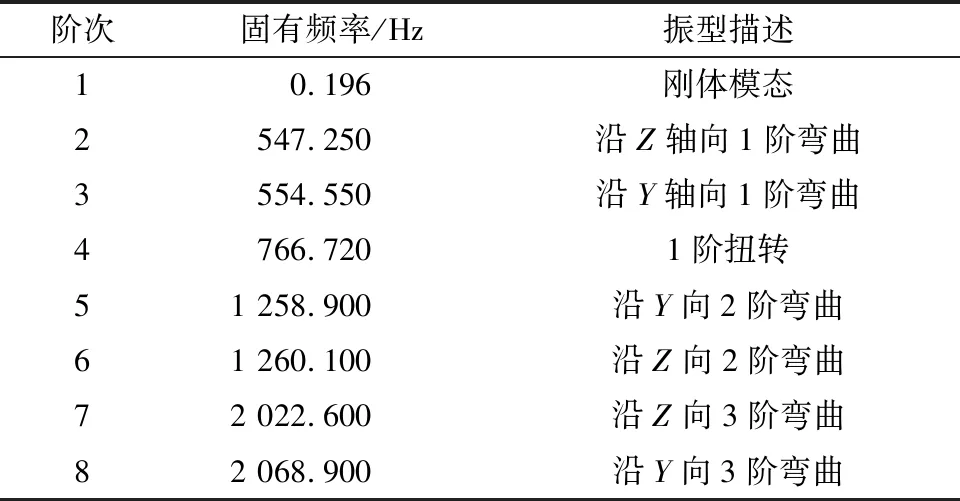
表1 转子系统固有频率Table 1 The natural frequency of the rotor system

4.2 临界转速计算

在Workbench中可以用Campbell图来表示模态频率随转速变化,得到转子在规定转速范围内的振动分量的变化特征,从而确定转子系统的临界转速。

使用Cylindrical Support(圆柱形支撑)作为约束条件,作用在轴颈A、F处的外圆表面上,同时固定径向、轴向自由度,释放切向自由度。对模型整体设置5种转速,确定X轴正方向为转轴法线方向。在求解器控制中打开阻尼选项,在转子动力学控制中打开科里奥利效应与Campbell图选项,点数量设定为5。最大模态阶数设置为8,此时模态分析是求解5种转速下对应的前8阶模态。Campbell图比率设置为1,并求解。转子系统Campbell图和临界转速与不同转速下的涡动频率表分别如图6和表2所示。

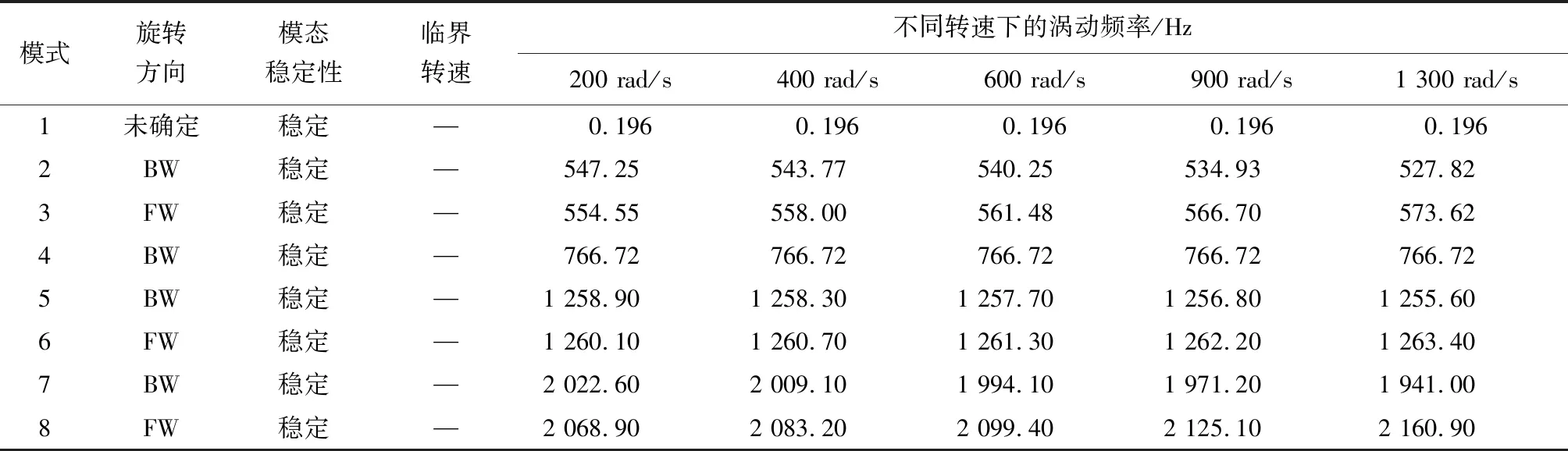
表2 转子系统临界转速与不同转速下的涡动频率Table 2 Critical speed of the rotor system and the vortex frequency at different speeds

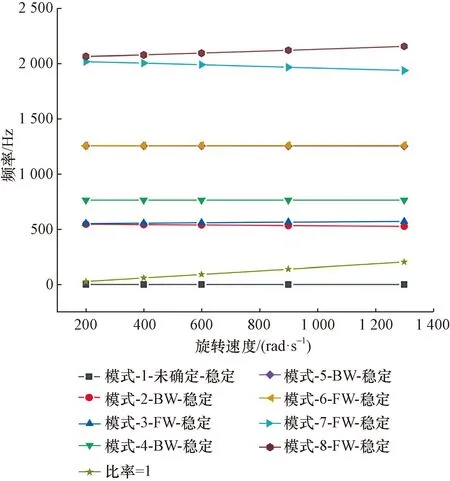
图6 转子系统Campbell图Fig.6 Campbell diagram of the rotor system

从图6可以看出,转子在200～1 300 rad/s的角速度范围内特征频率的变化相对平稳,等速线和各阶模态频率线没有任何交点,这说明转子系统在该转速范围内没有临界转速。从表2可以看出,第1行的频率值接近于0,这属于转动自由度的问题,由于计算临界转速的系统的质量矩阵、阻尼矩阵、刚度矩阵本身具有半正定性质,即行列式的系数是不小于0的,因此会出现1阶频率为0的情况,应当忽略这种情况下的结果。各转速下前8阶涡动方向以正反规律交替出现,每种转速情况下的涡动特性基本相同,一般来说旋转方向为反进动时模式都是稳定的,但正进动往往会提升转子刚性,从而增加振动的可能性,只有轴的转动与涡动方向是一致时才需要判断模式是否稳定。而模式稳定性的主要影响因素是轴承系统的刚度,它包括轴承自身的刚度和润滑油膜的刚度。

结合表2和图5可知,该转子系统第3、6、8阶为正进动,2、4、5、7阶为反进动,仅分析正进动的情况,发现主要变形出现在转轴跨中位置以及飞轮处,这和双盘转子系统本身的结构有关,是符合实际运行情况的。

4.3 谐响应分析

通过Workbench的谐波响应分析系统对双盘转子进行谐响应分析,在轴颈A、F处的外圆表面上添加转动副,连接类型为几何体-地面,扭转刚度、扭转阻尼可根据需要调整。在转轴跨中位置以分量形式定义激振力,Y分量10 000 N,Z分量10 000 N,同时定义Y相角90°,对转子右端施加200 N·mm的扭矩载荷。考虑陀螺效应,并将解法设置为完全法,分析整个系统在受给定激振力下在设定的扫频范围内的不同转速下的响应情况。

结合模态分析的结果可知一阶模态最大位移在转子跨中D处。首先研究固有频率约为554 Hz的幅频响应曲线,截取频率范围500～600 Hz,求解方案间隔设置为50,选取跨中位置查看变形结果,Z轴向的频率响应曲线如图7(a)所示,当频率从500 Hz增加到554 Hz过程中,该位置的径向位移逐渐增加,急剧上升达到峰值27.907 mm,此后迅速下降,然后缓慢降低。除近峰值区域外,其他频率处的振幅都很小,说明该转子有良好的动刚度,符合设计要求。同样也证明了该转子若发生共振会在近554 Hz区域带内,实际使用时该试验台三相伺服异步电动机最高工作转速远不会达到该频率,所以能有效地避开共振带。X轴向的频率响应曲线如图7(b)所示。该频域段内轴向位移最大值为8.61 μm,较于径向位移非常微小,因此转子主要表现为径向振动。

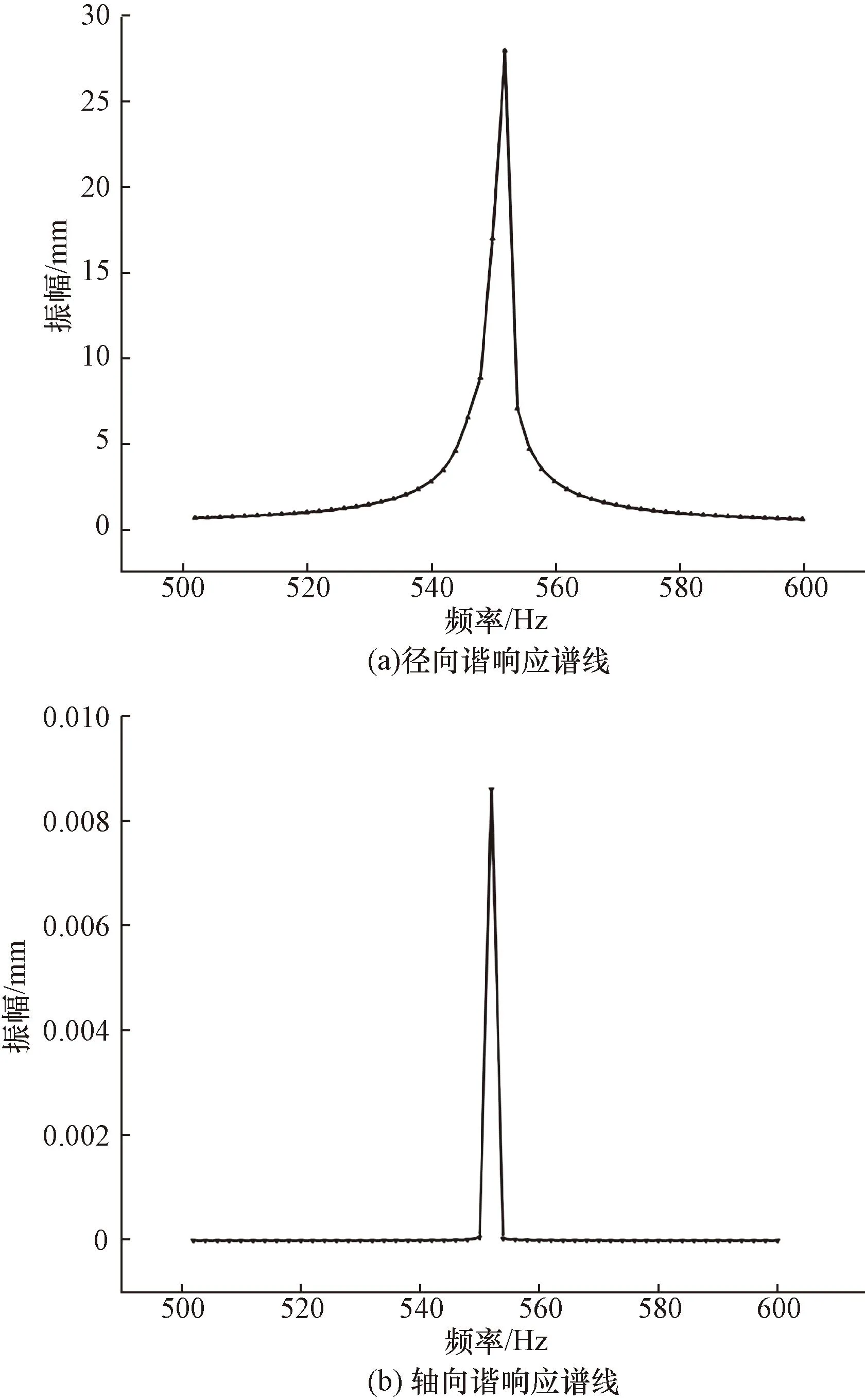
图7 转子谐响应分析结果图(500～600 Hz)Fig.7 Rotor harmonic response analysis result plot(500～600 Hz)

当转子在实际工作频率范围内运转时,即在一个相对低频的区域内分析,可得转轴跨中位置的径向谐响应谱线如图8所示。

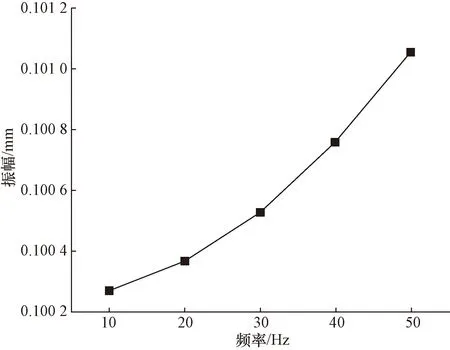
图8 径向谐响应谱线(0～50 Hz)Fig.8 Radial harmonic response spectral line(0～50 Hz)

在低频范围内,随着频率的增大,该位置的响应位移是逐渐增加的,在此区域内转轴跨中位置的最大位移在101.06 μm,是符合设计要求的。

5 实验研究

使用自制的旋转机械故障模拟试验台进行静模态实验分析,实验流程如图9所示。综合考虑现有的软件条件与实验条件,对转子使用锤击法进行多点激励单点拾振的轴承约束模态实验。实验设备是北京波谱品牌的WS-5294锤击测振系统,包括数据采集仪、台式计算机、压电式加速度传感器、力锤等[25]。

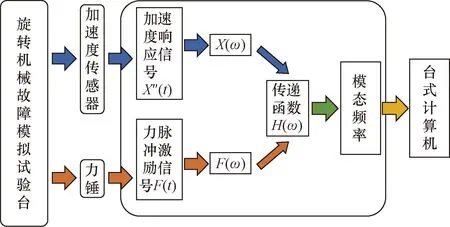
X(ω)为经过电荷放大及滤波、积分后由FFT算法处理为频域下的位移响应信号;F(ω)为经过电荷放大及滤波后由FFT算法处理为频域下的激励力信号图9 实验流程图Fig.9 Experimental flowchart

将传感器通过磁座吸附于预选点处,最后用信号传输线连接至数据采集仪上[26]。实验仪器连接如图10所示。

图10 实验设备图Fig.10 Diagram of experimental equipments

利用力锤依次敲击实验选取的24个测点,使用锤击测振系统软件获取转子前8阶固有频率。将实验所得结果与仿真结果进行比较,并计算相对误差。具体情况如表3所示。

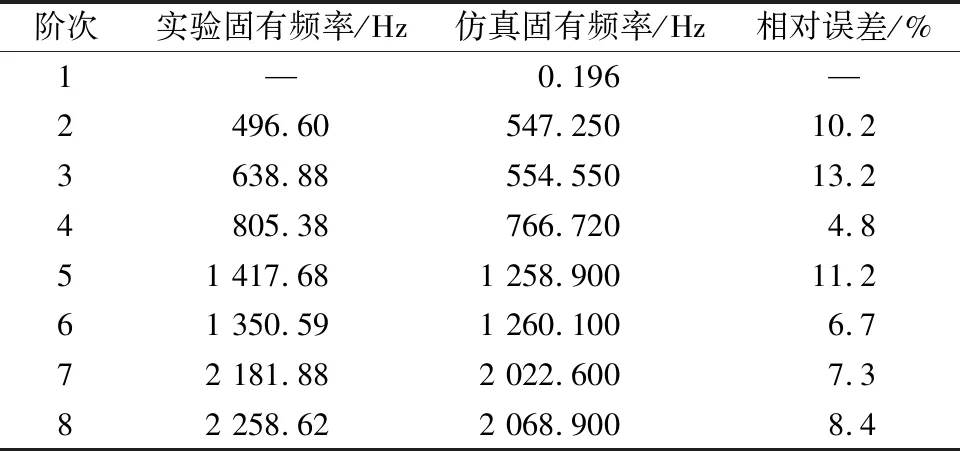
表3 仿真模态与实验模态对比Table 3 Comparison between simlation mode and test mode

根据表3可以看出,从实验模态测得的频率与有限元软件仿真分析获得的频率相对误差在15%之内。该误差出现的原因是有限元仿真中对实体模型进行了简化,并且使用力锤激励存在着实验误差[27]。综上所述,有限元仿真模型较为合理,仿真结果基本正确。

6 结论

(1)依据自制的旋转机械故障模拟试验台转子系统结构特点,阐明了动力学理论,使用SolidWorks软件建立双盘转子的三维实体模型,通过Altair Hyper Mesh软件划分了网格,在Ansys Workbench软件里进行后处理,为同类型转子的动力学分析提供了一定程度的参考。

(2)进行碰摩力下的转子静力学分析,通过选用仅压缩支撑约束条件正确反映了轴承内圈对转轴轴肩的应力情况,获取了最大应力位置。

(3)通过对双盘转子的模态分析与Campbell图计算,得知其在设定转速区间内并不会发生共振。了解获取临界转速的方法,为后续研究不平衡质量在临界转速区域内的响应提供了基础。

(4)通过谐响应分析研究整个系统在受给定激振力下在设定的扫频范围内的不同转速下的响应情况。转子跨中位置的动态变形很小,说明该转子有良好的动刚度,在低频范围内工作时,跨中位置最大变形101.06 μm,完全符合设计要求;同样也印证了该转子若发生共振会在近554 Hz区域带内。

(5)对转子进行了实验模态分析,并与仿真结果进行对比,误差在15%以内,从而验证了有限元模型的准确性。