波浪作用下平台吊放遥控水下机器人系统共振响应研究*

李文喆, 常安腾, 曹航语, 杜君峰

(中国海洋大学工程学院, 山东 青岛 266100)

随着海洋油气开发向深海发展,水下生产系统设备的应用越来越多,全世界有130多个海洋油气田应用了水下生产系统[1],水下安装、检测、探伤修复等深水作业需求重大,遥控水下机器人(Remotely operated underwater vehicle,ROV)在水下石油生产系统的运行维护中扮演非常重要的角色[2]。然而,在ROV投入作业前的下放过程中,动力现象复杂、风险大,因此在ROV的下放过程中保障其系统安全至关重要。

现阶段,人们对作业船舶吊放机器人做了一些研究。刘永林[3]采用时域和频域方法分析母船-吊缆-ROV系统的动力学特征,对垂直缆索运动特性进行了研究。徐诗婧[4]通过建立ROV多体耦合系统运动学和动力学模型,分析了母船-脐带缆-ROV多体耦合的运动学和动力学特性。顾永宁等[5]和任会礼等[6]采用数学建模的方法,对船舶-吊物系统进行耦合计算,得到吊物的共振区域范围。在这些研究中,主要针对的是采用母船进行ROV下放的过程。近年来,由于油气钻采平台直接下放ROV具有操作简单、灵活性高、经济性好等特点,因此越来越受到青睐。但深海石油钻采平台和作业船舶的水动力特性差异较大,整体系统动力响应特征不同,深海石油钻采平台下放ROV的过程需要进一步的深入研究。

在ROV的实际下放过程中,随着缆长的变化,吊缆-ROV系统的固有频率不断变化,在整个下放过程中,系统存在较宽的共振频率范围,且同波浪激励和平台运动发生共振或谐振的可能性较大。要安全、有效地下放,就需要对ROV下放过程中的共振机理和共振响应特性有清晰的认识。Driscoll等[7]通过对垂直吊放ROV系统进行了自由度相关性测定发现,起重船同ROV的垂向耦合运动明显。朱克强等[8]通过建立缆索系统垂向吊放解析模型,计算了系统固有频率,预测缆索松弛情况。王莹莹等[9]针对水下管汇下放,建立了运动方程,进而求解管汇发生轴向共振时的水深。综上可以看出,目前人们主要关注ROV的垂向共振,事实上,在ROV下放过程中更易发生共振,进而会引起吊缆的弯折。此外,ROV摆动幅度过大会引起较大的纵荡,从而会有ROV同平台及其附属用具发生碰撞的危险。

本文针对某深水半潜式钻井平台下放ROV的过程,使用Orcaflex建立平台-吊缆-ROV系统的耦合分析模型,采用时域方法研究波浪作用下ROV下放过程的共振响应及影响因素,重点关注ROV共振时的ROV摆动角度、吊缆张力、ROV纵荡响应,并给出了下放速度的取值建议以降低共振响应,对保障ROV的安全下放具有一定的工程意义。

1 计算模型

本文耦合模型如图1所示,通过钻井平台上的绞车将ROV于钻井平台的一侧进行吊放。其中,某半潜式钻井平台为双下浮体、四立柱、两组横撑、箱型甲板的船体型式,如图2所示。平台作业水深为1 000 m,作业工况下吃水19 m,排水量51 616.4 t。如图3所示,系泊系统分4组,共有12根系泊缆,系泊缆为锚链-聚酯缆-锚链三段式。应用商业软件HydroD计算平台运动的响应幅值算子(Remotely operated vehicle,RAO),结果如图4所示。

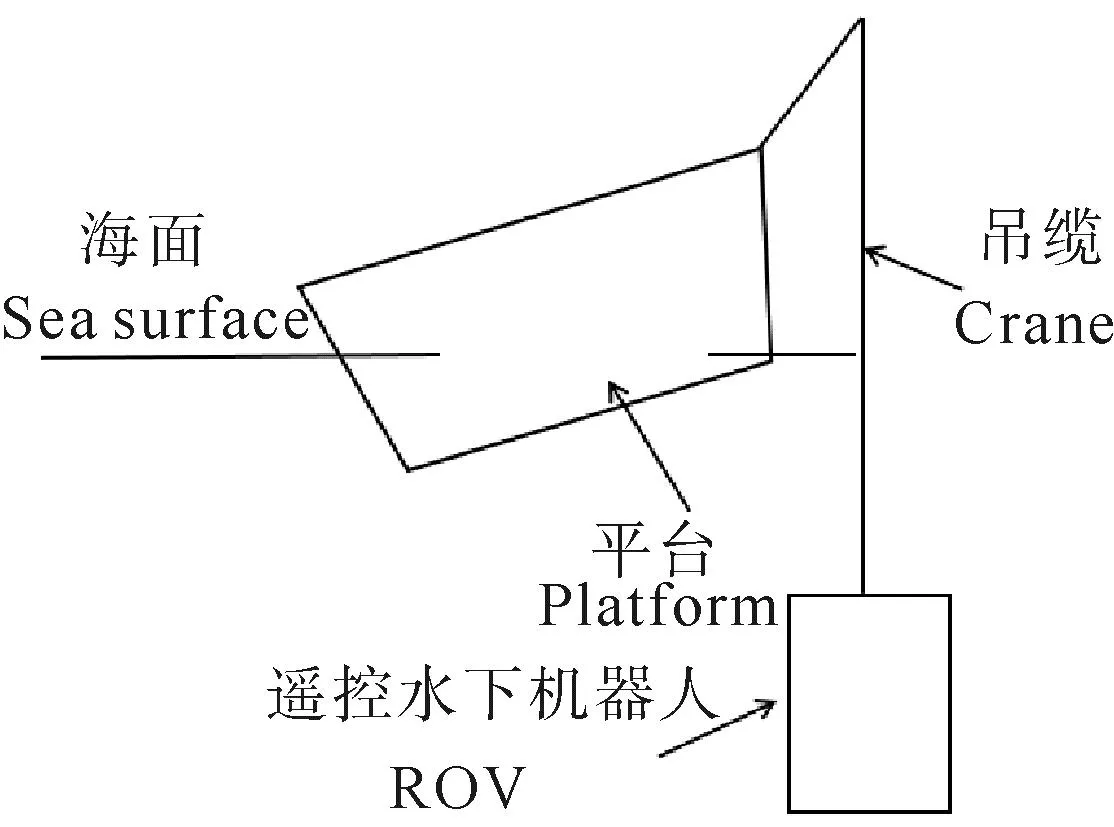
图1 耦合模型

((a)湿表面模型 Wet surface model; (b) 网格模型 Grid model.)

(①～分别为1～12号系泊缆。①～ are mooring cables from No.1 to No.12, respectively.)

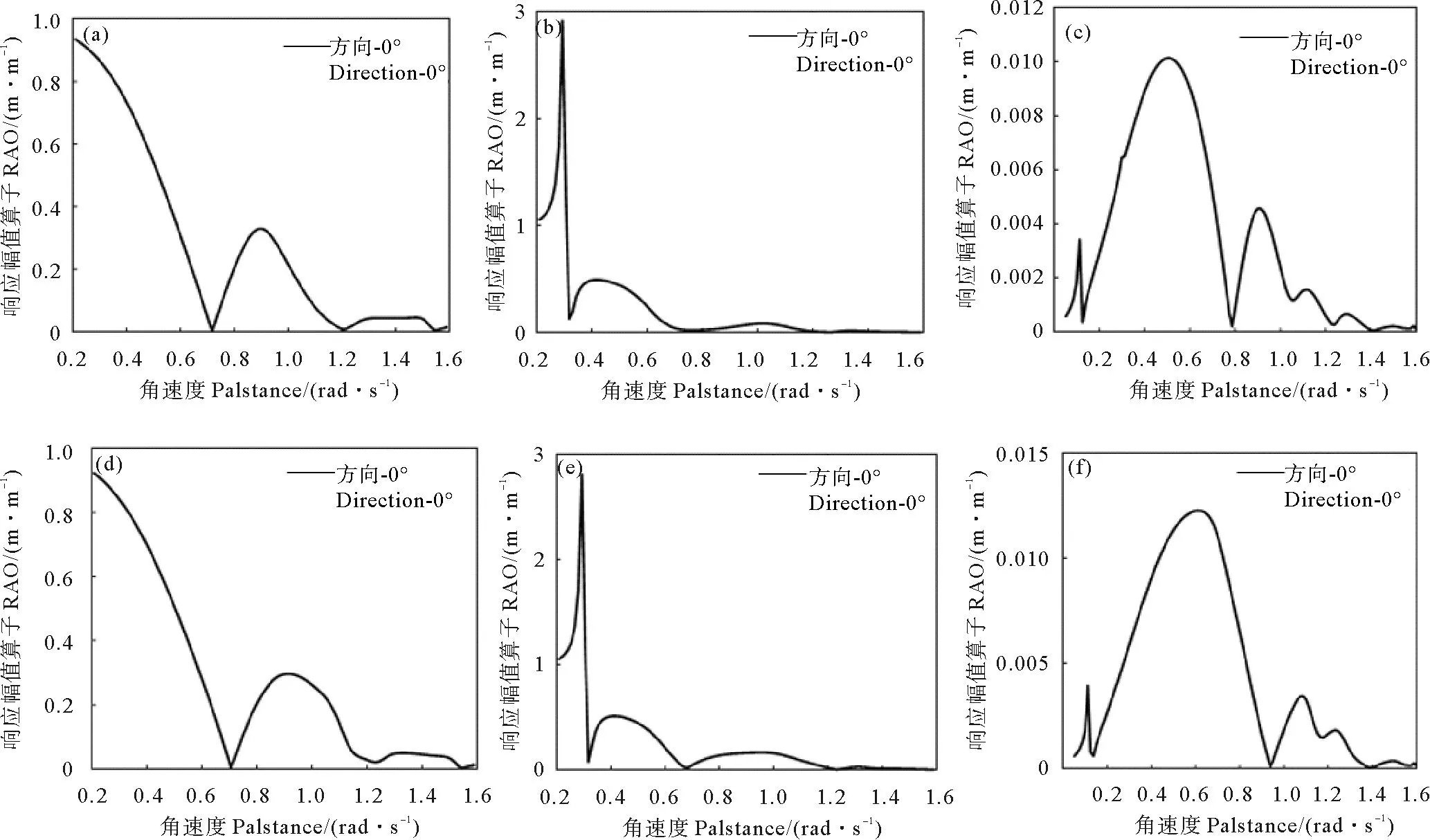
((a)纵荡RAO;(b)垂荡RAO;(c)纵摇RAO;(d)横荡RAO;(e)垂荡RAO;(f)横摇RAO。(a)Surge RAO;(b)Heave RAO;(c)Pitch RAO;(d)Sway RAO;(e)Heave RAO;(f)Roll RAO.)

ROV采用SAAB公司的某型号水下机器人,置于平台左侧,搭配8型中继器系统。为方便计算,将带有中继器的ROV模型简化为长方体,参考规范DNV-RP-H103[10],根据ROV形状简化计算得到水动力系数,用于ROV的运动响应分析。吊缆数据参考文献[11],吊缆和ROV的具体参数设置如表1和2所示。

表1 吊缆参数

表2 带有中继器的ROV参数Table 2 ROV parameters with TMS

2 空中下放阶段的ROV共振响应分析

基于频域水动力分析数据,考虑平台-吊缆-ROV的耦合运动,采用海洋工程软件Orcaflex对耦合系统进行时域分析,研究ROV在空中下放阶段的共振响应特性,分析不同吊缆长度的ROV共振响应。

首先,计算了4种缆长在2～10 s周期的单位波幅波浪作用下的ROV摆角幅值,如图5所示。

((a)吊缆长度5 m时的ROV摆角 ROV swing angel when the cable length is 5 m;(b)吊缆长度10 m时的ROV摆角 ROV swing angel when the cable length is 10 m;(c)吊缆长度15 m时的ROV摆角 ROV swing angel when the cable length is 15 m;(d)吊缆长度20 m时的ROV摆角 ROV swing angel when the cable length is 15 m.)

在波浪荷载的作用下,摆动幅值在特定波浪周期下出现峰值,ROV有明显的共振响应,当吊缆长度分别为5、10、15、20 m时,ROV摆动对应的共振波浪周期分别为4.5、6.5、7.9、8.9 s。

为进一步完整分析空中下放阶段中ROV的共振响应特性,进一步细化下放过程,得到空中下放阶段的吊缆长度、波浪周期和ROV摆动角度的三者关系图(见图6)。

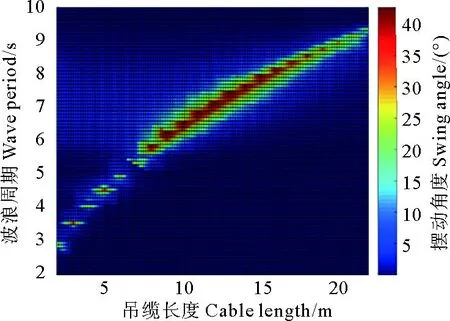
图6 吊缆长度、波浪周期、ROV摆动角度关系图

提取图6中的峰值点,分析下放缆长与对应共振周期的关系,并将ROV共振周期与单摆共振周期公式所计算的数值进行对比(见图7)发现,二者符合较好,误差均小于3%,即在空中下放阶段ROV摆动共振周期可用单摆固有周期计算公式进行估算,可在作业过程中进行快速分析。

图7 不同吊缆长度下的ROV共振周期统计图

此后,进一步分析共振时的ROV摆动角度同吊缆张力峰值关系(如图8)发现,吊缆顶端张力峰值同ROV摆动角度正相关。在吊缆长度为8～15 m时,由于ROV共振频率和平台纵摇RAO峰值对应的频率区域重合,加剧了吊缆-ROV系统的共振响应,因此出现摆动角度较大的情况。

图8 不同吊缆长度下的ROV摆动角度和吊缆张力峰值

结合图7和8可以看出,空中下放阶段的ROV共振波浪周期范围在2.8～9.3 s之间,尤其当波浪周期在5～8 s时,ROV共振响应尤为剧烈,这与平台纵摇RAO的一个峰值区域相对应(见图4(c))。

3 水中下放阶段的ROV共振响应分析

3.1 ROV水中下放的共振响应特性

本章研究ROV在水中下放阶段的共振响应特性。考虑ROV的水动力系数,选取不同的下放位置,计算不同吊缆长度的ROV共振响应结果运动响应。分析水中下放阶段的缆长同对应的共振周期的关系,并同单摆的共振周期的计算公式进行对比(见图9)发现,误差随缆长的增加不断增大。对单摆的共振周期公式进行修正如式(1)所示,修正公式估算共振周期误差能保持在4%以内,可为水中下放阶段估算ROV共振周期提供参考。

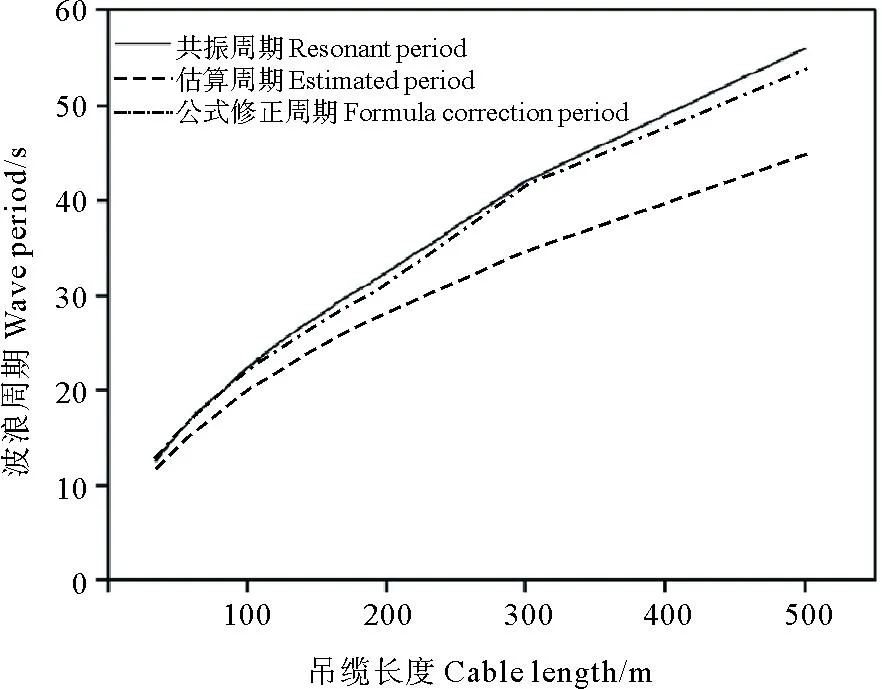
图9 不同吊缆长度下的ROV共振周期统计图

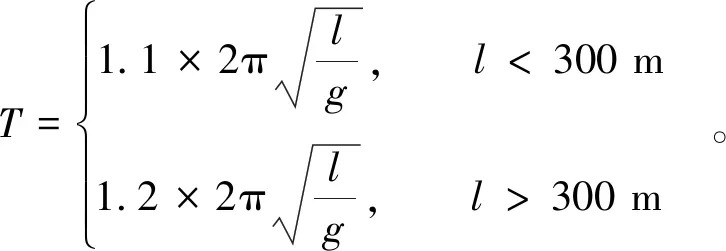
(1)

式中:T为ROV的共振周期;l为吊缆长度。

水中吊放时,ROV共振摆角幅值明显较空气中下放时小,这主要是因为海水对ROV和吊缆产生了较大的阻尼荷载;同时,吊缆长度的增加使吊缆-ROV系统在水中的阻尼增大,导致ROV的共振摆角随缆长的增加而减小。分析吊缆长度同ROV共振时的摆动角度和吊缆张力响应峰值的关系(见图10)发现,由于ROV的摆动角度较小,吊缆张力的动力项较小,张力主要受系统重力影响,因此吊缆顶端张力峰值随缆长的增加而增大,增加值主要来自于吊缆缆重的贡献。

图10 不同吊缆长度的ROV摆动角度和吊缆顶端张力峰值

3.2 流荷载对ROV共振响应的影响分析

考虑到流荷载对ROV运动响应的影响,对流速大小对ROV共振周期及共振响应的影响规律开展研究,结果见表3,发现流速越大,共振周期越大,ROV受到阻力越大,共振摆角则越小,但是对吊缆顶端张力峰值影响不大。

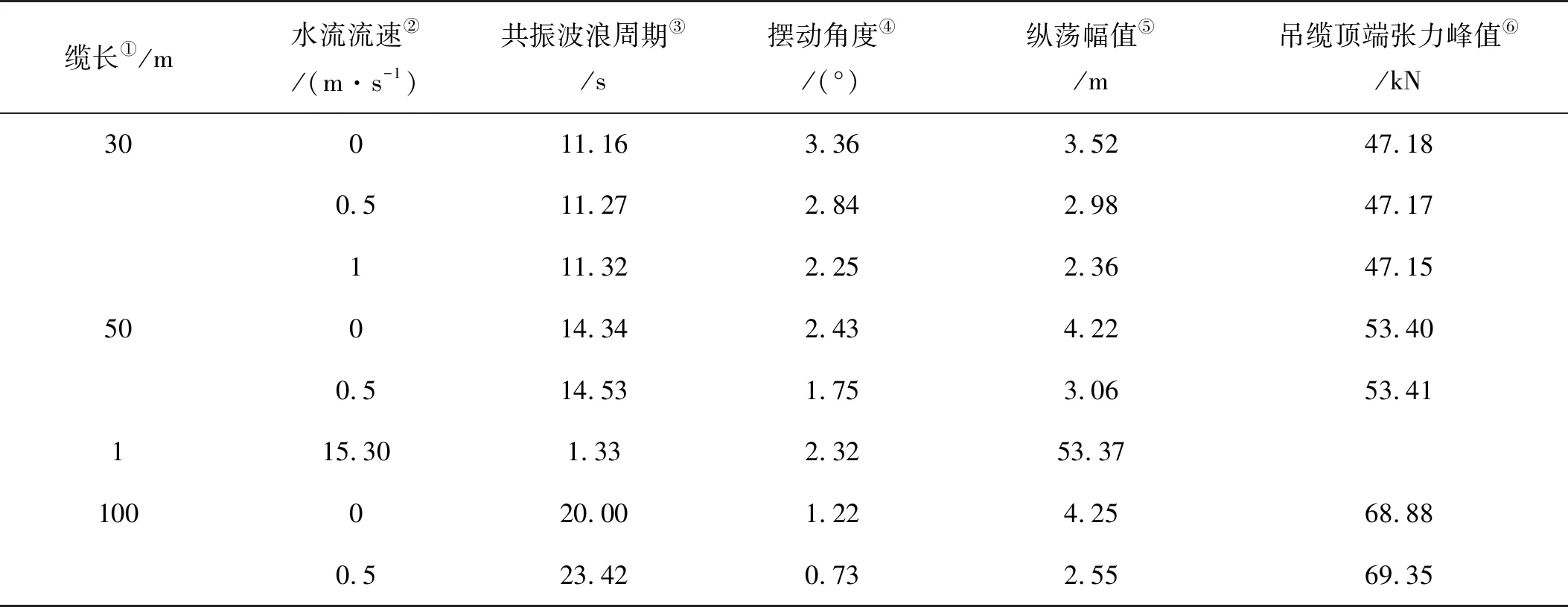
表3 特征缆长下,不同海流流速下ROV共振响应

4 ROV下放过程模拟分析

4.1 ROV下放过程中的共振分析

依据不同海区的波浪条件特征,选取特定作业工况,有义波高2 m,谱峰周期为8和16 s。设置吊点高度25 m,ROV起吊高度22 m,初始缆长3 m,下放速度0.1 m/s。对ROV连续下放过程进行分析,得到其动态响应,计算结果如图11和12所示。由结果可以发现,ROV下放过程中存在明显的共振现象。当谱峰周期Tp=8 s时,且ROV下放至120 s时,ROV纵荡和吊缆底端张力突然变大并持续到200 s,此时缆长伸长至15～23 m,对应的吊缆-ROV系统共振周期为7.8～8.3 s,固有频率为0.12～0.13 Hz,正好与波浪谱能量集中的频率区域相重合,如图13所示,激发系统产生共振响应;类似地,当谱峰周期Tp=16 s时,ROV下放至470 s时,ROV纵荡和吊缆底端张力变大并持续到550 s,此时缆长伸长至50～58 m,对应系统的共振周期为15.4～16.9 s,固有频率为0.05～0.06 Hz,与波浪谱能量集中的频率区域相重合,如图14所示。

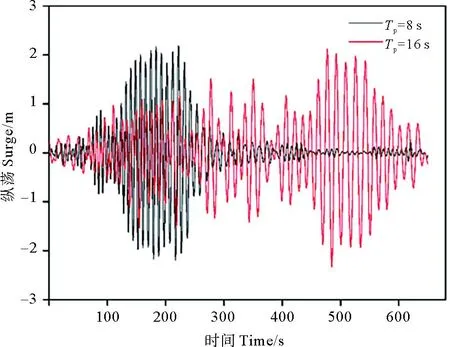
图11 下放速度为0.1 m/s时的ROV纵荡响应时历图

图12 下放速度为0.1 m/s时的吊缆底端张力时历图

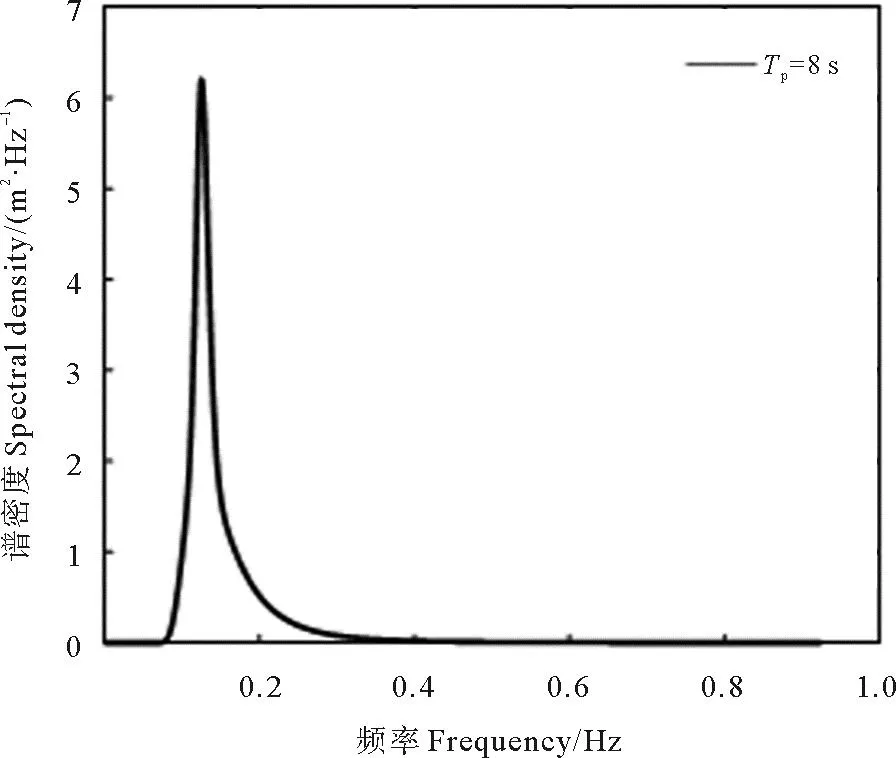
图13 谱峰周期Tp=8 s的波浪频谱

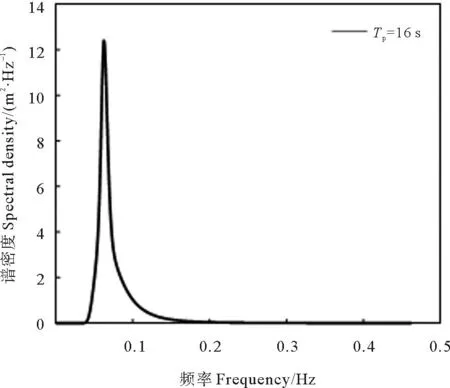
图14 谱峰周期Tp=16 s的波浪频谱

特别地,图12中出现张力骤降是因为随着吊缆的下放,ROV从空中下放至水中,由于海水给ROV提供了浮力,因此吊缆底端张力会出现突然减小的现象。吊缆张力出现较大波动区域的原因则是因为ROV处于共振区域,吊缆张力受系统的运动影响,因此吊缆底端张力随ROV运动响应的增大而出现较大的波动。

4.2 下放速度对共振现象的影响分析

考虑到不同下放速度可能对ROV下放过程中的共振现象的影响,本文针对4.1节中的第一个作业工况(有义波高2 m,谱峰周期为8 s),分别以0.1、0.2、0.3 m/s的速度下放ROV,响应时程如图15—16所示。

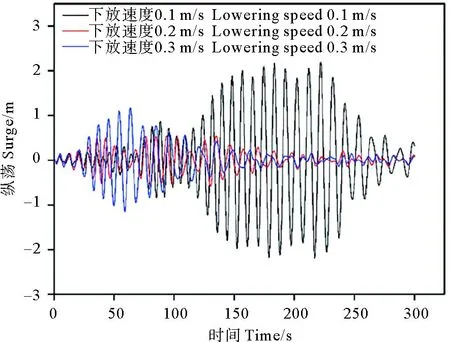
图15 谱峰周期为8 s时的ROV纵荡响应时历对比图

图16 谱峰周期为8 s时的吊缆底端张力时历对比图

可以看出,通过不同速度下放ROV都会存在共振问题,但相应特征差别明显,下放速度为0.2 m/s时,ROV的纵荡响应明显较其他两个速度下放时的响应小。因此,在该海况下作业时,推荐以0.2 m/s的速度进行ROV的下放。

5 结论

(1)空中下放阶段,ROV的摇摆共振周期可通过单摆固有周期计算公式进行估算;吊缆顶端张力峰值同ROV摆动角度正相关。ROV共振频率与平台纵荡RAO峰值所对应的频率区域重合时,将导致ROV共振更加剧烈。

(2)水中下放阶段,通过本文修正的单摆共振周期计算公式可相对准确地对ROV共振周期进行估算。由于吊缆-ROV系统在水下存在阻尼,ROV共振响应相比空中阶段大幅度减小。考虑流荷载的影响,水流速越大,ROV共振周期越大,ROV共振摆角越小。由于ROV的摆动角度较小,所以吊缆张力的动力项较小,因此张力主要受系统重力影响而随缆长增加而增大。

(3)选取典型的作业工况,对ROV的连续下放过程进行模拟,响应时程显示存在明显的共振段,共振响应区域对应的系统固有频率范围与波浪谱能量集中的频率区域重合。ROV下放速度对下放过程中的共振响应有显著影响,可通过选择合适的下放速度以降低ROV共振响应,保障系统安全。