循环荷载作用下含水合物粉细砂的残余变形*

孙宏鑫, 张 安, 王 栋**, 马慧龙

(1. 中国海洋大学海洋环境与生态教育部重点实验室, 山东 青岛 266100; 2. 中国海洋大学海洋地球科学学院, 山东 青岛 266100)

0 引言

天然气水合物是一种由甲烷分子和水分子在低温高压下形成的笼型结晶化合物,广泛分布于陆地永久冻土区和大陆架边缘海底地层中,是一种储量丰富的新型能源[1]。在海洋环境中,开采井筒承受的循环风浪荷载最终传递给水合物储层[2],井筒设计和水合物储层稳定性评价都需要考虑含水合物土的循环强度和变形特性。以往对含水合物土的试验[3-9]与本构理论[10-17]研究主要集中在静荷载,国内外已完成的循环加载试验还很有限。Zhu等[18]进行了有限数量的循环三轴试验,试图获得含水合物土在地震荷载作用下的循环强度。循环荷载导致含水合物土中的超孔隙水压力累积,土体强度和刚度降低,显著影响应变的发展,因此还需要描述动力应变的发展过程。

循环荷载下残余应变预测模型主要分为两类:弹塑性模型和经验方程。当模拟高循环次数的加载时,弹塑性模型通常导致较大误差[17]。而经验方程可直接表征残余变形随载荷循环次数的变化,例如Monismith[19]提出软黏土的残余应变与循环次数的关系:

εr=ANb。

(1)

式中:εr是残余剪应变;N是循环次数;A和b是拟合参数,取决于土体性质和应力状态。其它类型残余应变与循环加载次数之间的关系类似式(1),关键影响因素在参数A和b中表示,包括初始应力状态(动剪应力σd、有效围压σ3′、超固结比等)、排水条件和加载条件(循环荷载波形和频率、主应力轴旋转等)。类似式(1)的多个模型[2,20-28]已用于海床响应和路基沉降等问题。对于特定密实状态的一般砂土,残余应变主要依赖循环应力比CSR和有效围压σ3′[27],循环应力比定义为CSR=σd/(2σ3′)。

本文进行含水合物粉细砂的三轴不排水循环加载试验,定量探索循环应力比、有效围压和水合物饱和度对残余应变的影响。基于一系列试验结果,总结残余应变和孔隙水压力特性,改进Monismith公式,提出预测残余应变的简化公式。

1 试验方案

使用福建建材标准砂,筛除0.5 mm粒径以上的砂粒,所得试样级配曲线见图1。最大孔隙比emax= 0.91,最小孔隙比emin= 0.59,颗粒比重为2.65,平均粒径为168 μm。

图1 试验粉细砂的级配曲线

含水合物试样的合成与剪切均在中国海洋大学的高压低温三轴试验仪内完成,该装置已在我们之前的工作中[29]介绍,它可以模拟水合物原位生成和分解等多种工况,研究不同有效围压、温度和饱和度等条件下的沉积物强度、变形和渗透率等特性,在计算机系统上可以输出应力、应变、围压、孔压和时间等试验测试结果以及多种试验曲线。水合物储层大多埋藏在海底以下100～300 m,取循环加载试验有效围压σ3′为1和3 MPa,饱和度Sh目标值为0%和40%,在给定的有效围压和水合物饱和度下,进行不同循环应力比的不排水剪切试验,具体方案见表1。荷载频率为0.1 Hz。试验步骤如下。

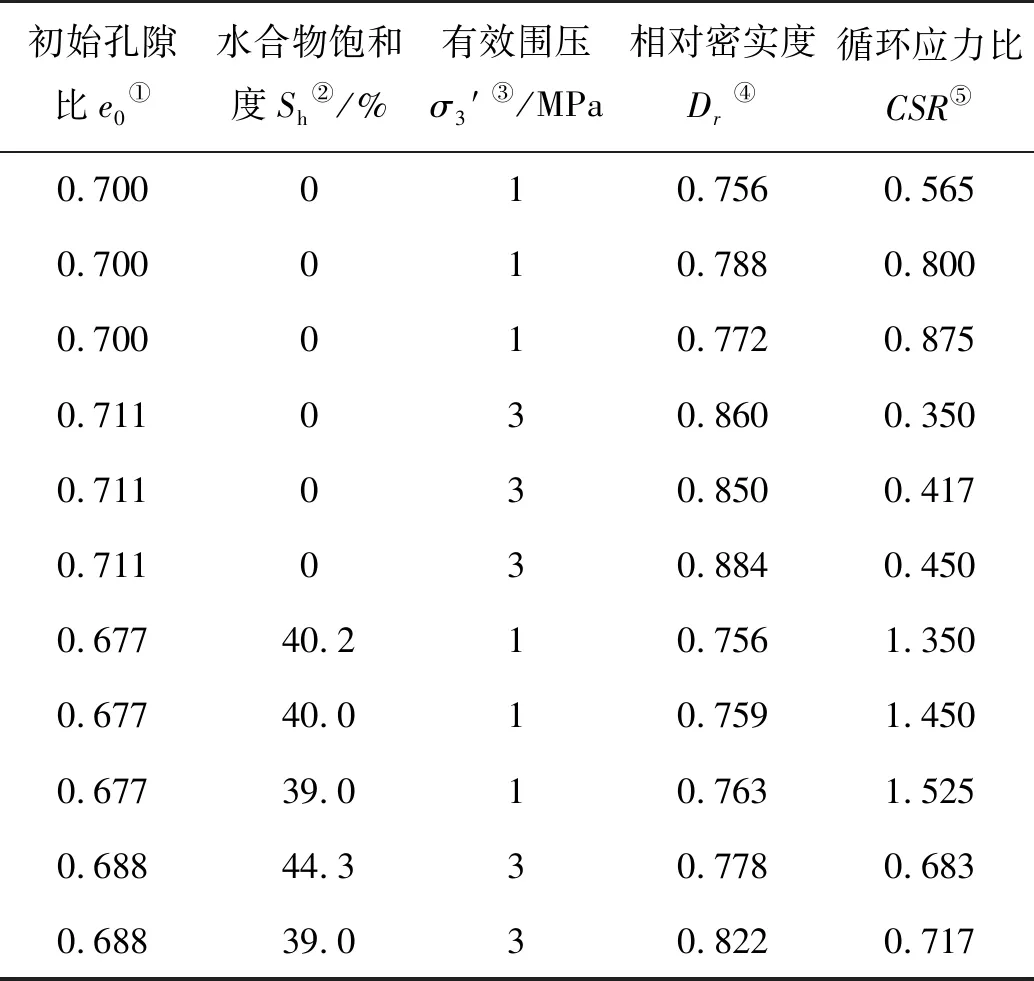
表1 试验方案

(1)将目标饱和度所需的蒸馏水量与目标孔隙比所需的砂粒进行混合。

(2)将混合后的砂样分为10等份,在制样器中均匀击实,制得试样高约100 mm,直径50 mm。套两层乳胶膜,单层乳胶膜厚度为0.5 mm。

(3)将试样放入围压仓密封,围压仓内注满硅油,通过围压泵施加100 kPa压力维持试样的形态稳定。

(4)进行气饱和,通甲烷气排出试样内的空气,继续缓慢注入甲烷气至气压达到4.4 MPa,气体注入过程中保持围压比气压高200 kPa。压力达到目标值后将温度降至1 ℃,达到水合物合成条件,并维持48 h以充分合成。

(5)水合物生成后,维持温度和围压,进行水饱和,将试样上下两端连接两个反压泵,通过底部反压泵向试样通入蒸馏水以排出多余的甲烷气,充满后从试样顶部流进顶部反压泵,调节试样底部和顶部压力,使进水速度控制在4 mm3/s,进水过快可能破坏水合物结构,而过慢则可能与残余的甲烷气形成新的水合物。水饱和维持48 h。

(6)将试样顶部阀门关闭,施加1或3 MPa的有效围压进行固结,通过反压体积变化,计算试样体变,每小时体变小于0.05%视为固结完成。维持围压和温度,对试样进行不排水循环剪切,当轴向应变达到20%或试样破坏时,停止试验。

2 试验结果分析

2.1 典型试验结果

本节给出了纯净砂和含水合物粉细砂试样在循环荷载下的典型试验结果,包括应力-应变曲线、应变与循环次数关系曲线和孔压与循环次数关系曲线。其中,εa为轴向应变,偏应力q=σ1′-σ3′。

图2为典型的应力-应变曲线,从图中可以看出,初始加载阶段,偏应力随轴向应变增加,与王兆祥等[29]和赵志超等[30]的静三轴试验结果一致。含水合物粉细砂在循环荷载作用下的轴向应变大致可分为稳定型和破坏型两种,当循环应力比较低时,试样最终达到稳态,循环应力比较高时,试样破坏。

图2 循环加载的剪应力-轴向应变关系曲线

图3为图2中应力-应变曲线所对应的应变与循环次数关系曲线。如图3(a)所示,轴向应变可分为残余部分εr和循环部分εc。随着循环次数的增加,循环应变在开始时增加,随着残余应变趋向于稳定而达到稳定的值,残余应变在初期加速增加,中期平缓,如果达到剪切破坏,则可能加速增加。残余应变是本文关注的重点。

图3 循环加载的典型应变时程曲线

图4为图2中应力-应变曲线对应的超孔压曲线。在图4(a)和(b)中,纯净砂试样在加载初期产生正超孔压。而图4(c)和(d)表明,含水合物试样的孔压发展模式与纯净砂不同。Ghiassian等[31]的静三轴试验表明,含水合物砂在剪切过程在会产生负超孔压,本文循环三轴的试验也发现了类似的现象。如图4(c)所示,由于水合物的胶结和填充作用,含水合物砂在1 MPa有效围压加载下呈现剪胀趋势,导致负超孔压。在图4(d)中,当有效围压增加到3 MPa,水合物砂在加载前期呈现剪缩趋势,引起正超孔压,但35次循环后孔压迅速下降,可能的原因是:前期孔压累积导致有效围压降低,含水合物粉细砂的结构发生渐进性破坏,剪切带形成(见图5),试样由剪缩转变为剪胀,从而导致孔压下降。

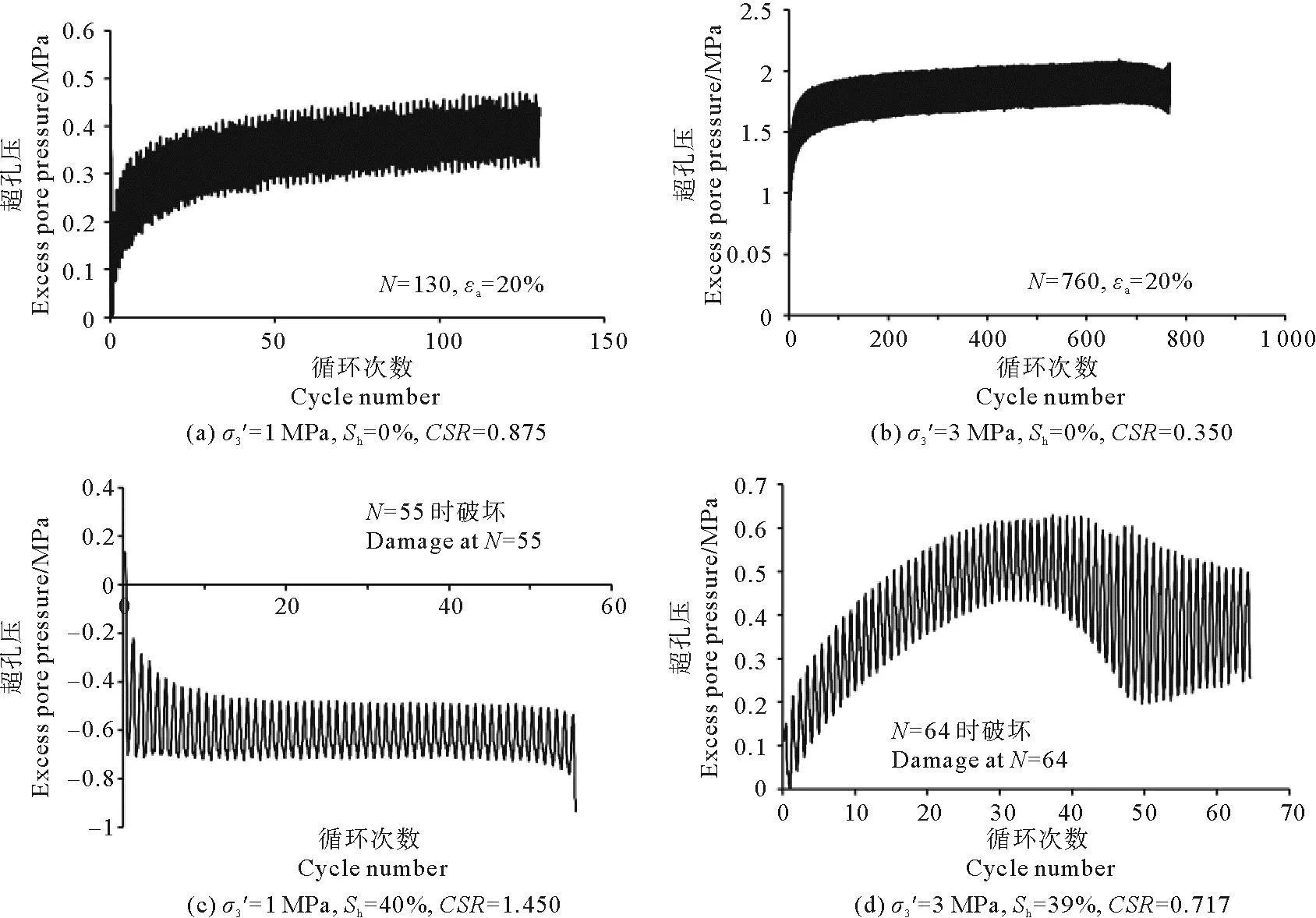
图4 循环加载下的典型超孔压时程曲线

(σ3′=3 MPa,Sh=39.0%,CSR=0.717。)

2.2 残余应变表达

2.2.1 确定指数bMonismith等[19]和Li等[28]认为式(1)中的指数b不受循环应力比影响,Ren等[27]主张指数b取决于土体类型和土体物理性质(如相对密实度),是给定的常量。为检验指数b的变化,整理循环三轴试验结果:对式(1)等号两侧取对数,然后线性拟合未破坏阶段,图6为典型试验结果,不同循环应力比、有效围压和水合物饱和度条件下,粉细砂残余应变和循环加载次数的双对数曲线存在线性关系,斜率b基本一致。

(σ3′ = 1 MPa,Sh≈40%。)图6 双对数坐标下残余应变与循环加载次数曲线的斜率拟合

图7所示进一步给出参数b与循环应力比、有效围压和水合物饱和度之间的关系。参数b大多位于0.32～0.39区间,建议取为0.34,其标准差Sd= 0.041。对双对数坐标下残余应变与循环加载次数曲线的未破坏阶段重新线性拟合,取拟合线斜率为0.34,得到11条拟合线的平均决定系数R2= 0.978,高R2和低Sd表明拟合参数b取值的合理性,b值与循环应力比、有效围压和水合物饱和度无关。

图7 不同试验条件对参数b的影响

2.2.2 确定系数A式(1)中的系数A代表第一次循环加载后土体的残余应变。图8为四种不同条件下A随CSR的变化曲线,循环应力比、有效围压和水合物饱和度对系数A的影响都不容忽略。观察图8所示的趋势,系数A与循环应力比的关系接近幂函数,与归一化有效围压σ3/σatm和Sh的关系可视为对数函数。σatm为标准大气压,取101 kPa。系数A可近似表示为:

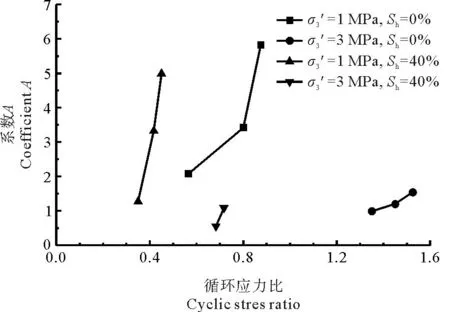
图8 系数A随CSR的变化曲线

A=a1CSRa2exp(a3σ3′/σatm)exp(a4Sh)。

(2)

式中:参数a1代表土体的典型残余应变值[32];a2、a3和a4代表循环应力比、有效围压和水合物饱和度对残余应变的影响。采用多元非线性回归拟合第一次循环加载后土体的残余应变,得到a1=1.873、a2=3.8、a3=0.137 5和a4=-7.7。

2.2.3 残余应变预测公式 结合式(1)和(2):

εr=a1CSRa2exp(a3σ3′/σatm)exp(a4Sh)Nb。

(3)

式(3)预测的残余应变与试验结果的比较见图9。相同的循环次数下,CSR越大,残余应变越大,并且初始残余应变随着CSR的增加而增加。式(3)的预测数据与试验数据较接近,只有图9(d)中CSR=0.683时误差较大,这可能是由于试验误差。

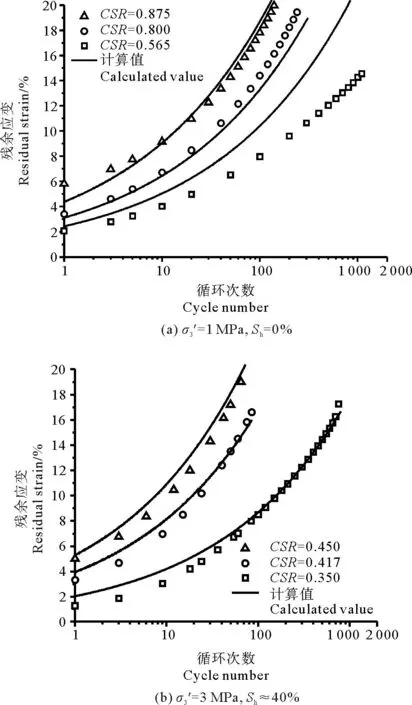
图9 残余应变预测值与实测值的比较

3 结论

对含水合物粉细砂进行了一系列不同有效围压、水合物饱和度和循环应力比的不排水循环三轴试验,研究了轴向应变和超孔隙水压力的发展规律,提出残余应变预测公式,得到结论如下:

(1)水合物的存在增强了土体的剪胀性,含水合物粉细砂在低有效围压下循环加载产生负超孔压。而有效围压增大减弱了土体剪胀性,导致超孔压累积的趋势。

(2)在双对数坐标内,残余应变和循环加载次数呈线性关系。不同循环应力比、有效围压和水合物饱和度条件下,直线斜率b基本不变。

(3)循环应力比、有效围压和水合物饱和度对残余应变的影响体现在第一次循环加载造成的残余应变A,A随循环应力比增大、随有效围压和饱和度的增加而减小。

(4)提出了一个同时考虑循环应力比、有效围压和水合物饱和度的残余应变预测公式,预测结果和实验数据吻合较好。