利用机器学习从切片的孔隙结构特征预测多孔介质渗透率

孟胤全，蒋建国，吴吉春

南京大学 地球科学与工程学院，表生地球化学教育部重点实验室，南京 210023

确定多孔介质的渗透率对于地下水运动、油气开采、二氧化碳地下封存以及核废料泄漏等问题的研究具有重要意义（Neuman, 2005；Tsang et al.,2015；Zhou et al., 2019）。达西压力梯度法（Miguel and Serrenho, 2007）测定多孔介质渗透率的周期较长且受环境干扰较大，因此无法大量应用。随着计算流体力学的快速发展，孔隙尺度的多孔介质流体流动数值模拟已经广泛应用于计算渗透率。然而，复杂的边界条件与非线性的Navier-Stokes 方程使得数值模拟计算成本较高，从而限制了多孔介质的计算尺寸。根据达西定律，多孔介质的渗透率由孔隙空间结构决定，两者之间映射关系可转化为机器学习有监督问题。前人选择使用随机森林模型、梯度提升模型、人工神经网络（ANN）和卷积神经网络（CNNs）等等机器学习回归模型预测多孔介质的渗透率（Araya and Ghezzehei, 2019 ；Rabbani et al.,2020 ；Srisutthiyakorn et al., 2016）。

作为计算机视觉领域最为经典的模型, CNNs已被广泛用于预测多孔介质数字图像所对应的渗透率（Kamrava et al., 2019；Tang et al., 2022；Tian et al., 2020；Wu et al., 2018）。然而，孔隙空间结构数据量、CNNs 模型的复杂度与GPU 内存之间的矛盾限制了多孔介质的研究尺寸与模型的预测性能（Kashefi et al., 2021）。例如，尺寸为256×256×256立方体素的三维多孔介质数字图像具有超过1000万个体素，直接输入至复杂度高的深层3D CNN 时会给GPU 带来巨大的负担。然而降低CNNs 模型的复杂度会导致欠拟合从而降低预测性能，增加GPU 的内存或数量则会大幅增加计算成本。因此前人考虑应用多孔介质领域的专家知识对孔隙空间结构进行手动特征提取，而后再输入至机器学习模型中。Kashefi 等人将孔隙—固相边界的位置信息提取为点云数据并输入至点云神经网络，大幅度降低了模型的数据输入量并取得了很好的预测结果。此外，平均曲率积分、多点相关函数等孔隙空间结构特征也往往作为人工神经网络（ANN）或支持向量机回归（SVR）或XgBoost 等机器学习模型的输入（Rabbani et al., 2019 ；Röding et al., 2020 ；Tian et al., 2020）。然而提取多孔介质孔隙结构特征参数的过程往往复杂而较难实现，且参数一旦冗余并且经过组合后输入至机器学习模型中，则该模型应用于渗透率值范围窄且样本量少的多孔介质数据集时，会产生明显的过拟合（Tian et al., 2020）。因此，本研究考虑一种易于理解与实现的孔隙结构特征提取方法，能够通过机器学习模型有效地建立起孔隙结构特征参数与渗透率的映射关系。

多孔介质的切片在空间上是连续的，可视为一种空间序列（Zhang et al., 2022）。对于任意一个多孔介质，本研究提取其所有切片的单一孔隙结构特征以形成一个多维向量。该向量中的元素数即多孔介质的切片数。切片的孔隙结构特征保留了空间的连续性，所组成的向量因此可视为序列数据。我们将其作为经典机器学习模型与长短期记忆神经网络（LSTM）模型的输入。LSTM 模型在自然语言处理（NLP）、语音翻译等序列建模问题上取得了许多成功（Hochreiter and Schmidhuber, 1997），本文采用该模型来处理切片孔隙结构特征的连续性。

本文首先介绍多孔介质的生成和获取方法、切片的孔隙结构特征提取方法。其次介绍 3 种常用的经典机器学习模型与长短期记忆神经网络模型的原理。再次，介绍模型的应用方法并以两个案例展示模型在测试集上的预测性能。而后讨论本研究方法的优势。最后，对文章内容进行总结。

1 数据与方法

1.1 数据准备

应用有监督机器学习模型预测多孔介质渗透率的前提是获取足够多的样本，包括三维的多孔介质数据与对应的渗透率值。在实践过程中采用成像技术获取大批量真实孔隙结构断层扫描数据受时间、经济成本的制约（Song et al., 2019）。而为了提高效率，利用数值模拟来生成多孔介质这一方法被广泛采纳（Graczyk et al., 2020；Volkhonskiy et al.,2022）。本文采用沉降法生成由球状颗粒填充的多孔介质（Vold, 1960；Pilotti, 1998），如图1 所示。直径可变的球颗粒从顶部依次释放，在下落过程中如果其中一个颗粒撞击到另一个颗粒，则该颗粒会沿着下部颗粒的表面下落。这一下落过程一直持续到颗粒势能达到局部最小值，此时该颗粒与其他三个球颗粒接触或撞击到底部。此沉降法生成的多孔介质保留了真实孔隙结构的拓扑特征，但孔隙度通常大于0.4。为降低孔隙度，我们将部分球颗粒的直径扩大10%，使得孔隙度降低至0.38 以下，同时配位数保持不变。我们采用周期性边界条件，将球颗粒沿x和y轴周期性放置。

图1 生成多孔介质的示意图Fig. 1 The schematic diagram of the generation of porous media

多孔介质的渗透率k由达西定律计算得出，即u=k ∆P/L，其中u为平均流速，∆P是压力差，L是多孔介质在流动方向上的长度。因此，当计算出水流的平均流速u时即可确定渗透率值k。Navier-Stokes 方程描述具有复杂几何边界的多孔介质中的水流，而格子玻尔兹曼方法（LBM）采用简便的反弹方案处理无滑移边界条件，是求解Navier-Stokes方程的有效手段。本文采用LBM 的D3Q19 模型首先计算出多孔介质中z轴方向水流的平均流速，然后再根据达西定律计算出多孔介质在该方向上的渗透率（Qian et al., 1992；Wolf-Gladrow, 2004）。

应用上述方法本研究生成了1000 个由球颗粒填充的多孔介质（图2a）并计算出了相应的渗透率值，我们将其作为研究案例1。此外，我们还从公开可用的DeePore 多孔介质数据集（Rabbani et al., 2020）中随机选取了5000 个多孔介质样本（图2b）, 其渗透率通过孔隙网络模型（PNM）计算得出，我们将其作为研究案例2。

图2 本研究使用的两类多孔介质Fig. 2 Two types of porous media used in this study

1.2 特征提取方法

本研究认为，三维多孔介质由空间中连续的二维切片构成，从而形成一种空间序列。切片的孔隙结构特征在空间上仍然具有连续性，因此可视为一组序列数据。本研究将三维多孔介质表示为由二维孔隙结构特征参数所组成的多维向量，由于向量的元素具有连续性，我们称此类向量为特征序列。特征序列的长度即向量的维数、切片的数量。

长期以来，含有孔隙度、比表面积这两个全局物理参数的半经验公式Kozeny-Carman 方程（Carman，1939）被广泛应用于预测多孔介质的渗透率。本研究提取多孔介质切片的孔隙度与比表面积，分别组成孔隙度序列与比表面积序列来表征三维多孔介质（图3）。切片的孔隙度和比表面积可以表示为数字图像像素的函数。孔隙度是孔隙像素数与总像素数之比。二维孔隙结构的比表面积定义为孔隙总周长与其总面积之比（Rabbani et al., 2014；Yu et al., 2009），本研究将比表面积表示为孔隙—颗粒边界的像素数与孔隙像素数之比。此外，本研究还考虑了切片孔隙结构的连通性并以图像欧拉数来表示（Ohser et al., 2002 ；Shamsi et al., 2021 ；Vogel et al., 2010）。作为图像拓扑性质的量度，欧拉数由孔隙部分的连通分支与其中固相颗粒之差确定。对切片图像进行旋转、拉伸等操作并不会改变欧拉数，且欧拉数越小，孔隙的连通性越好。我们借助scikit-image 包，以4-邻域（1-连接）的模式提取每一切片的图像欧拉数。

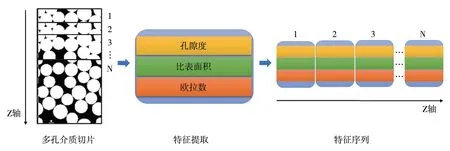
图3 提取多孔介质切片特征的示意图Fig. 3 Schematic diagram of extracting slice features of a porous medium

本小节以4 个样本为例，说明特征序列具有表征多孔介质孔隙空间结构的能力。我们采用沉降法生成两个孔隙度为0.38 的多孔介质作为样本1 与样本2，两者分别由直径为0.3 mm、0.6 mm的球颗粒填充，z轴方向上的尺寸为400。我们从DeePore 多孔介质数据集中选取两个孔隙度为0.10、z轴方向上的尺寸为256 的岩石样本作为样本3 和样本4。我们将这些样本沿着z轴方向表示为切片序列（图4），然后由特征提取方法得到每个样本的孔隙度序列、比表面积序列和欧拉数序列（图5）。对于固相均为球颗粒且孔隙度相同的样本1 与样本2，两者孔径不同这一信息隐含在各自特征序列的震荡中。对于非均质性更强的样本3 与样本4，即便孔隙度相同，由不同地质条件所形成的孔隙空间结构以及由此产生的特征序列都能够将两者明显区分开。因此，我们通过特征提取方法建立的序列能够表示任意的多孔介质并且不会存在重复。我们计算每个样本的三种特征序列两两之间的相关度，并以Pearson 相关系数表示，结果如图6 所示。我们发现，对于样本1 与样本2 而言，两者的孔隙度序列与比表面积序列的Pearson 相关系数都接近-1，说明由球颗粒填充的多孔介质其孔隙度序列与比表面积序列线性相关性高，且为负相关。而孔隙度序列与欧拉数序列虽然也为负相关，但线性相关性明显减弱。两个样本的比表面积序列与欧拉数序列的Pearson 相关系数分别为0.77 与0.66。对于样本3 与样本4 而言，孔隙度序列与比表面积序列之间仍然有很高的负线性相关性，但是欧拉数序列与孔隙度序列或比表面积序列的线性相关性则显著减弱。在本研究中，代表多孔介质孔隙空间结构的特征序列可以作为经典机器学习模型或长短期记忆神经网络模型的输入。三种特征序列也可以合并为一个多维数组而后输入至长短期记忆神经网络中。

图4 沿z轴方向不同位置的多孔介质切片Fig. 4 Slices of the porous media at different positions along the z-axis direction

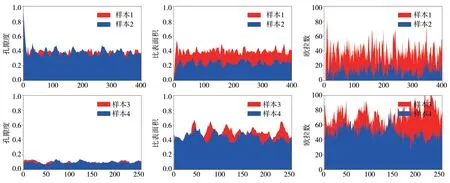
图5 多孔介质的特征序列Fig. 5 Feature sequences of the porous media

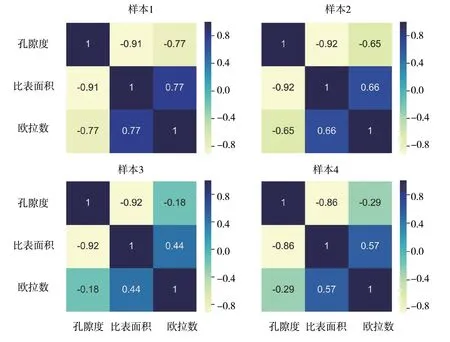
图6 特征序列的Pearson 相关系数热图Fig. 6 Pearson correlation coefficient heat map of feature sequences

1.3 机器学习方法

本研究采用经典机器学习模型k近邻（KNN）、随机森林（Random Forest）、支持向量机回归（SVR），长短期记忆神经网络（LSTM）来预测多孔介质的渗透率。算法介绍如下。

k近邻算法会寻找最接近输入样本的其他k个训练样本并以它们的平均标签值作为模型的预测结果（Cover and Hart，1967）。k近邻模型的复杂度由最近邻数量k控制，k值越小则表示模型越复杂。随机森林是一种相对简单的bagging 集成算法（Breiman, 2001），旨在训练多个随机且独立的决策树从而提供更好的预测结果。支持向量机回归算法使得所有样本数据接近超平面并保持总偏差最小（Cortes and Vapnik, 1995），模型采用结构风险最小化原则来学习数据特征，可以很好地处理小样本集的非线性或高维回归问题。

长短期记忆神经网络LSTM 是循环神经网络（RNN）的变体（Hochreiter et al., 2001），通过门控机制来控制网络中信息的流动和记忆，可以有效解决反向传播过程中的梯度消失或梯度爆炸，往往适用于时间序列建模问题。LSTM 的网络结构和工作流程如图7 所示，网络中引入长期状态ct来存储特定时刻的历史信息，并将该信息非线性地输出到隐藏层的外部状态ht。长期状态ct的计算公式如下：

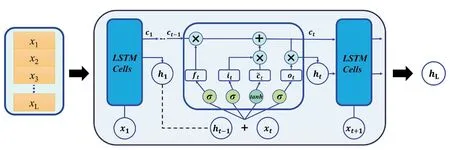
图7 长短期记忆神经网络结构示意图Fig. 7 Schematic diagram of the structure of long short-term memory neural network

其中ft∈[0,1]D、it∈[0,1]D与ot∈[0,1]D分别是控制信息传输路径的遗忘门、输入门与输出门。⊙表示向量对应元素的乘积，ct-1是上一时刻的长期状态，c~t是通过双曲正切函数得到的候选状态，其定义为：

遗忘门、输入门与输出门的计算公式如下：

其中W*、U*与b*均为神经网络的可学习参数，* ∈{c,i,f,o} 。

在水文地质领域，LSTM 模型广泛应用于降雨径流模拟预测、洪水预测以及地下水位预测等水文模型的预测预报问题（Ni et al., 2020 ；Xiang et al.,2020 ；Zhang et al., 2018）。本研究将LSTM 模型的时间记忆和预测能力应用于空间序列问题。我们通过PyTorch 平台开发并训练输入了不同特征序列的LSTM 模型。经典机器学习模型与LSTM 模型的预测性能通过决定系数R2和均方根误差RMSE 两个指标来评价，定义如下：

其中n是多孔介质的样本量，与分别表示样本i的真实渗透率与预测渗透率，表示所有的平均值。

2 模型结果与讨论

2.1 模型应用方法

首先，令X1，X2，X3，…，XN表示多孔介质样本集。向量Xn=[x1x2…x400]表示案例1 中的第n个样本，Xn=[x1x2…x256]则表示案例2 中的第n个样本。向量Xn即通过上文特征提取方法取得的孔隙结构特征序列，向量的元素数等于多孔介质的切片数，同时也是LSTM 模型的时间（空间）步长。令Yn（n=1，2，3，…，N）表示第n个样本的渗透率。其次，将多孔介质的特征序列X=[X1X2X3…XN]与渗透率标签值y=[Y1Y2Y3…YN]按照7∶3的比例划分为训练集（Xtrain，ytrain）与测试集（Xtest，ytest）。再次，应用训练集（Xtrain，ytrain）对经典机器学习模型进行交叉验证与网格化参数搜索以确定相对最佳的超参数。对于LSTM 模型，应当确定数据的输入结构、神经网络的结构、损失函数以及优化器等等。经过数次测试可以确定适当的批量大小（batch size）、epoch、学习率以及其他超参数。LSTM 模型在每个时刻（空间中的位置）输入向量Xn的一个元素。代表同一多孔介质的不同Xn向量可合并为一个多维数组，此时LSTM 模型在每个时刻（空间中的位置）的输入是来自不同 向量的元素组合，即切片孔隙结构特征参数的组合。这种处理方式在案例2 中进行了展示。而后，应用搜索到的超参数训练模型。训练集输入至LSTM 网络中，网络的权重在训练过程中由反向传播算法与优化器不断调整。最后，将测试集（Xtest，ytest）代入训练完成的模型中，并以决定系数R2和均方根误差RMSE 定量描述模型的预测性能。

2.2 案例1：由球颗粒填充的多孔介质

本案例样本集包含了1000 个利用沉降法生成的多孔介质，相应的渗透率通过LBM 计算得出。多孔介质的尺寸为128×128×400 立方体素，体素尺寸为20 μm。渗透率均匀分布在33 Darcy 与800 Darcy 之间，平均值为416 Darcy，标准差为220 Darcy。三维多孔介质的孔隙度范围为0.27~0.38，平均值为0.34，标准差为0.03。本研究定义三维多孔介质的比表面积为孔隙—颗粒边界处的体素数与孔隙体素数之比，其范围为0.25~0.62。应用6-邻域（1-连接）模式，我们还计算了多孔介质的三维欧拉数以表示其连通性。本案例多孔介质的孔隙空间结构参数如表4 所示。应用特征提取方法，含有6553600 个体素的多孔介质被压缩成维数为400 的向量，也即特征序列，数据压缩率为99.994%。我们将孔隙度序列、比表面积序列和欧拉数序列分别输入至经典机器学习模型与LSTM 模型中。为促进模型收敛，训练过程中我们对渗透率值取log。经典机器学习模型通过Python scikit-learn 进行训练与测试。模型的超参数通过交叉验证与网格搜索得到，表现最佳预测性能的超参数组合如表1、表2 和表3 所示。

表1 k近邻模型的超参数Table 1 Hyperparameters of k-nearest neighbor model

表2 随机森林模型的超参数Table 2 Hyperparameters of random forest model

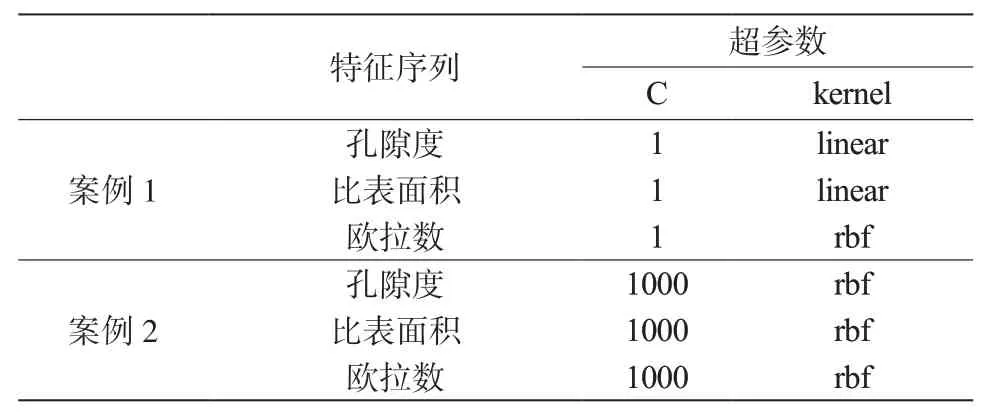
表3 支持向量机回归模型的超参数Table 3 Hyperparameters of support vector machine regression model

表4 案例1多孔介质的属性Table 4 Properties of porous media in case 1

各个模型的预测结果如图8 所示。在经典机器学习模型中，我们比较输入不同特征序列的模型各自的预测结果。输入比表面积序列的k近邻、随机森林以及支持向量机回归均取得了各自最佳的预测结果，R2分数分别为0.981、0.979 和0.972，RMSE 损失分别为0.041、0.043 和0.050，而输入孔隙度序列的k近邻和随机森林则取得了各自最差的预测结果，R2分数分别为0.974 和0.948。输入欧拉数序列的支持向量机回归同样表现不佳，R2分数为0.965，RMSE 损失为0.056。

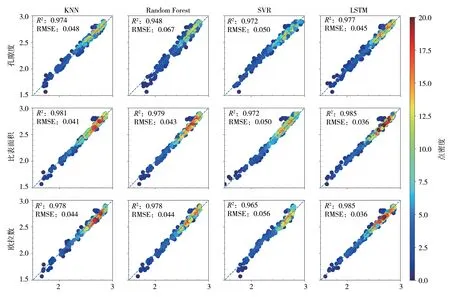
图8 案例1中模型的预测渗透率（logD）和真实渗透率（logD）的对比Fig. 8 Comparisons of predicted permeability (logD) and true permeability (logD) of models in case 1

与上述经典机器学习模型相比，长短期记忆神经网络LSTM 模型的预测能力有明显提升。我们将3 种特征序列分别输入至LSTM 模型中。由PyTorch平台搭建的神经网络结构设置如下。当神经网络的超参数batch first 设置为True且输入尺寸设置为1 时，输入张量的大小为batch size×sequence length×1。考虑到样本量较少，故选择较小的batch size 更为合适，经尝试后batch size 设置为16。且本案例的多孔介质其切片数为400，因此输入张量的大小为16×400×1。本模型将4 个LSTM 层堆叠在一起，参数num_layers 设置为4，并将hidden_size，即隐藏状态h的特征数量设置为2048。LSTM模型将其学习到的孔隙结构序列知识保存在外部状态ht中。如图7 所示，我们将序列中最后一个位置的ht，即hL，输入至两层全连接神经网络，网络节点依次为2048 和1。输入孔隙度序列、比表面积序列与欧拉数序列的LSTM 模型，初始学习率分别设置为1e-5、1e-4 以及1e-3。训练过程中我们选择Adam 优化器并将 epoch 设置为500，当epoch为50、150、250、350 时，学习率分别固定为初始学习率的0.1、0.05、0.025 和0.01 倍。网络的其余超参数采用默认值。本研究使用一块NVIDIA Tesla v100 16GB GPU 来训练模型，训练过程持续4 小时。如图8 所示，输入孔隙度序列、比表面积序列和欧拉数序列的LSTM 模型，其R2分数分别为0.977、0.985 和0.985，RMSE 损失分别为0.045、0.036 与0.036，预测结果优于经典机器学习模型。

上述结果说明了以下两点：（1）相比于输入其他两种特征序列，每个输入比表面积序列的模型均可提供较好的预测结果，这表明比表面积序列能够更好地表征多孔介质的孔隙空间结构；（2）具备序列处理能力的长短期记忆神经网络LSTM，可以更有效地建立特征序列与渗透率之间的映射关系，取得比经典机器学习模型更高的预测分数。

2.3 案例2：来自DeePore数据集的多孔介质

Rabbani 等(2020) 开发了一套名为DeePore 的深度学习工作流程，能够基于显微断层扫描图像快速估计出多孔介质的渗透率。DeePore 多孔介质数据集基于60 个真实岩石的显微断层结构，通过改变孔隙度与图像增强等方法将样本量扩充至17700。他们假定多孔介质为各向同性，并采用孔隙网络模型（PNM）计算出x、y和z方向上渗透率的算术平均值，其单位为像素的平方，像素尺寸为5 μm。 此外，他们提取多孔介质的三个垂直中平面并分别为它们计算固相与孔隙之间的距离变换，将结果堆叠后再用作2D CNN 的初始特征图，该模型的R2分数为0.9。

本案例从DeePore 多孔介质数据集中随机选择5000 个尺寸为256×256×256 立方体素的样本。渗透率的范围为0.001~134 Darcy，平均值为10.6 Darcy，标准差为15.10 Darcy；孔隙度的数值范围为0.1~0.45，平均值为0.27，标准差为0.10。其余的孔隙空间结构参数如表5 所示。

表5 案例2多孔介质的属性Table 5 Properties of porous media in case 2

本案例依然使用交叉验证与网格搜索方法来获取经典机器学习模型的超参数。与案例1 的不同之处在于LSTM 模型的输入，我们此次合并三种特征序列来共同表征多孔介质的孔隙空间结构，其中欧拉数序列进行了标准化。每一个具有16777216 个体素的DeePore 多孔介质样本被压缩成维数为256 的向量，或是尺寸为256×3 的数组。模型的预测结果如图9 所示。在三种经典机器学习模型中，输入比表面积序列的k近邻取得了最高的R2分数0.963 与最低的RMSE 损失0.119。随机森林和支持向量机回归在输入比表面积序列时同样取得了相对较好的预测结果。我们由此认为，比表面积序列更适合表征多孔介质的孔隙空间结构。LSTM 模型的网络层数与案例1 相同，而hidden_size 增加至4096。初始学习率与batch size 分别设置为1e-4 与32。全连接层的结构以及其他相关超参数的设置与案例1 保持了一致。我们使用一块NVIDIA TITAN RTX 24GB GPU来训练模型，训练过程持续约26 小时。经过500 个epoch 后，LSTM 模型的R2达到0.984，而RMSE 为0.077。与经典机器学习模型中结果最好的k 近邻相比，LSTM 模型的R2提升了2.18%，RMSE 降低了35.29%。此外，LSTM 模型还可以合并更多的多孔介质孔隙结构序列数据使得模型的鲁棒性进一步提升，而这是经典机器学习模型无法做到的。

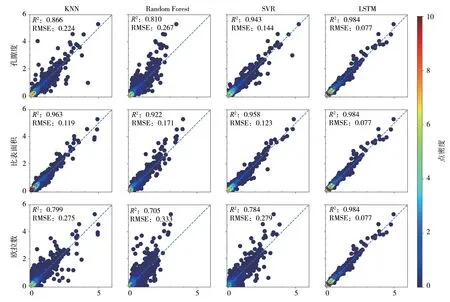
图9 案例2中模型的预测渗透率（px2）和真实渗透率（px2）的对比Fig. 9 Comparisons of predicted permeability (px2) and true permeability (px2) of models in case 2

2.4 讨论

本研究提出，由多孔介质切片的孔隙度、比表面积和欧拉数所组成的特征序列可表征孔隙空间的结构。将这三种特征序列输入至经典机器学习模型中，模型可以在数秒钟内完成训练并给出可靠的预测结果。在案例1 中，输入比表面积序列的模型表现最好，输入欧拉数序列的模型次之，而输入孔隙度序列的模型表现最差；在案例2 中，输入比表面积序列的模型表现最佳，其次是输入孔隙度序列的模型，而输入欧拉数序列的模型表现最差。由此可见，比表面积序列相对于另外两种特征序列，能够更好地表征多孔介质的渗透能力，而欧拉数序列虽然在案例1 中表征能力相对于孔隙度序列要好一些，但对于孔隙空间结构更加复杂、随机的案例2 样本，欧拉数序列便无法有效地表征多孔介质的渗透能力。深度学习长短期记忆神经网络LSTM模型在两个案例中的预测性能优于经典机器学习模型，训练时间分别为4 小时和26 小时。我们将输入特征序列的LSTM 模型与直接输入数字图像的3D CNN 模型在同一多孔介质数据集上进行比较，两者的预测结果基本一致，但前者的训练效率更高：具有4 个卷积层、卷积核尺寸为4×4×4 且特征图输出尺寸为64×8×8 的3D CNN 模型，在案例2中取得的R2为0.987，RMSE 为0.068。我们将3D CNN 模型的epoch 设置为150，训练时间持续66小时，平均每个epoch 用时26.4 分钟，而LSTM 模型平均每epoch 仅需3.12 分钟。

两个案例的多孔介质样本在形状尺寸、孔隙结构和渗透率计算方法上存在显着差异，因此我们采用迁移学习方法来验证LSTM 模型的泛化性能。我们用案例1 较少的样本集对案例2 中训练完成的LSTM 模型进行重新训练：应用300 个训练样本预测出其余700 个样本的渗透率值。渗透率的单位为保持统一，已由Darcy 转化为像素的平方。训练时长为4.65 小时，R2分数为0.959，RMSE 损失为0.109。考虑到案例2 由PNM 计算得到的渗透率与真实值之间存在5%~30%的简化误差（Rabbani et al., 2020），LSTM 模型的泛化能力是相当好的。我们认为，输入特征序列的长短期记忆神经网络LSTM 模型在前期应用大量样本训练完成后，对于从未见过的、陌生的多孔介质样本集，可以借助样本集的少量训练样本为其余样本提供准确的渗透率预测结果。此外，深度学习模型的预测性能与训练样本量呈正比是当前公认的事实，我们可以预见，如果增加训练样本量使LSTM 模型得到充分的再训练，预测准确度会有明显提升。

3 结论

本文提出了一种直观的方法来提取多孔介质切片的孔隙结构特征并将它们组成向量。向量中的元素保留了切片的空间连续性，故我们称此类向量为特征序列。本研究提取多孔介质每一张切 片的孔隙度、比表面积和欧拉数，分别构建孔隙度序列、比表面积序列与欧拉数序列来表征多孔介质的三维孔隙空间，而后应用3 个经典机器学习模型与深度学习长短期记忆神经网络LSTM 模型来预测多孔介质的渗透率。我们设置了两种孔隙结构差异明显的多孔介质数据集作为研究案例。研究结果表明，输入比表面积序列的模型相较于输入另外两种特征序列的模型能够取得相对更好的预测结果，说明比表面积序列更能代表多孔介质的孔隙空间。此外，具备序列信息处理能力的LSTM 模型，其预测结果相比于经典机器学习模型更好。在案例1 中，输入比表面积序列的LSTM 模型其R2分数为0.985，RMSE损失为0.036。在案例2 中，输入特征序列数组的LSTM 模型其R2分数为0.984，RMSE 损失为0.077。用案例2 样本集训练完成的LSTM 模型，当应用于案例1 时，仅需要少量样本对模型进行再训练，同样可以给出良好的预测结果。

就目前而言，大多数预测多孔介质渗透率的机器学习框架都以CNNs 为主，但三维多孔介质的数据量、神经网络的复杂度以及GPU 的内存限制使得该方法计算成本高昂。本研究提出的特征提取方法能够有效降低多孔介质的数据量，使机器学习模型在保持较高预测准确度的同时，大幅降低计算成本。此外，长短期记忆神经网络LSTM 模型能够从特征序列中学习切片的空间连续性，这对于今后研究多孔介质的三维重建尤为重要。