基于VMD-LSTM-ELMAN模型的国际原油价格人工智能预测研究

廖婧文

香港浸会大学 工商管理学院,香港 999077

原油作为一种基础能源、化工原料和战略物资,是当今世界不可或缺的资源。它不仅和人们的生活息息相关,而且对世界各国的政治、经济、环境等方面都具有极其重要的影响(Kilian and Vigfusson,2011;任泽平,2012;包湘海等,2014;张跃军,2020)。1983年,纽约商业交易所推出的轻质低硫的西得克萨斯州中间基原油(West Texas Intermediate,WTI)期货合约拉开了原油期货交易的序幕。由于期货合约交易市场的迅速发展,逐渐使得能源价格与各个领域产生了密切的关系(Steve,2010;张金良等,2013)。事实上,在市场供需博弈、美元汇率、投机交易、地缘冲突、自然灾害等因素的综合作用下,国际原油价格呈现出高噪声、非线性和非平稳的特征,导致对其的精确预测变得十分艰难。由此,构建科学的国际原油价格预测模型成为学术界关注的焦点(Huang et al.,2021;王德运等,2022;刘玲等,2022)。

也正因为如此,相当一部分学者运用计量经济学模型预测原油价格。徐凌等(2013)建立了自回归积分滑动平均模型(Autoregressive integrated moving average,ARIMA)对国际油价进行定量预测;包湘海等(2014)通过构建原油价格和世界人均国内生产总值的回归模型预测国际原油价格;熊熊等(2016)将季节因子加入ARIMA模型中,对2014—2020年的国际原油价格进行预测。尽管上述计量经济学模型能够较好地刻画原油价格序列中的线性特征,但却存在难以拟合原油价格序列中非线性特征的缺陷。为此,国内外学者引入更为先进的人工智能模型对金融时间序列进行预测。

随着计算机技术的迅速发展,人工智能方法在预测领域广受国内外学者的关注,包括人工神经网络(Artificial Neural Network,ANN)及其相关模型(Guresen et al.,2011;Adhikari et al.,2014)。使用ANN对金融时间序列进行预测所得到的实证结果证实了 ANN预测的有效性(Khashei et al.,2014);能源价格可以基于自适应学习处理的反向传播神经网络(Back propagation neural network,BPNN)被预测(Rumelhart et al.,1986)。此外,支持向量回归(Support vector regression,SVR)在现有研究中被认为是一种有效的预测方法(An et al.,2020),混沌映射、萤火虫算法和SVR可以用于对股票市场价格进行预测(Kazem et al.,2013)。虽然上述模型在预测金融时间序列方面具有优势,但不可避免地存在对短期信息保持记忆的缺陷。ELMAN(Elman neural network)神经网络的反馈结构有利于短期信息的保留,因此具有较强的优化计算和联想记忆功能,从而在能量价格的预测中具有优势(Li et al.,2019)。同时,混合量化ELMAN神经网络在短期负荷预测方面的应用证明了该模型的优越性(Li et al.,2014)。递归神经网络(Recurrent neural network,RNN)能够利用隐藏层的自反馈机制存储近期事件的记忆信息(Lin et al.,1998;Arjun et al.,2020),而LSTM(Long short-term memory network)作为RNN的改进模型,不仅可以解决梯度爆炸和梯度消失的问题,而且可以学习长期依赖信息(Bengio et al.,1994;Hochreiter et al.,1997)。使用包含LSTM的混合模型预测碳价格,有效地提高了预测精度(Zhang et al.,2020)。因此,针对原油价格序列具有时变性与长记忆性的特点,本文引入ELMAN神经网络和LSTM模型进行预测。

需要进一步指出的是,原油价格通常在多因素的影响下具有非平稳、高噪声特征,而信号分解方法能捕捉其动态变化,为模型提供足够丰富的信息(Lin et al.,2022)。经验模态分解(Empirical mode decomposition,EMD)、集成经验模态分解(Ensemble empirical mode decomposition,EEMD)和其他基于EMD的算法被认为是数据分解的有效方法(Wang,2017;Li et al.,2018;Cao et al.,2019;Yu et al.,2019)。然而,上述分解算法缺乏基础理论,存在边界效应和对噪声敏感等缺点,可能严重影响预测结果的准确性(Liu et al.,2020)。VMD是一种严格的非递归分解技术,通过在谱域对原始序列进行若干特定带宽模式的处理,将原始序列分解成多个具有不同特征的本征模函数(Intrinsic mode function,IMF)(Dragomiretskiy et al.,2014;Abdoos,2016;Wang et al.,2017)。不仅如此,国内外学者通过大量实证分析同样证实了VMD模型在挖掘时间序列中隐藏的非线性和非平稳特征方面具有显著优势(Zhu et al.,2019;Sinvaldo et al.,2020;Sun et al.,2020;Huang et al.,2021)。

由于单一模型难以捕捉原油价格序列的多重特性,因此结合分解技术与预测模型而构建的混合模型受到许多学者的广泛关注(唐小我,1992)。张金良等(2019)基于VMD和果蝇算法优化的最小二乘支持向量机(Least squares support vector machine,LSSVM)构建了混合预测模型,并证实了该预测方法对WTI价格具有良好的预测性能。前馈神经网络(Feedforward neural network,FNN)被用于分别对EMD分解的IMFs进行预测,最后应用自适应线性神经网络(Adaptive linear neural network,ALNN)模型集成多个IMFs的预测结果,实证结果表明分解集成方法的预测性能优于单一的神经网络模型(Yu et al.,2008)。杨云飞等(2010)结合EMD和支持向量机(Support vector machine,SVM)对原油价格进行预测。奇异谱分析(Singular spectrum analysis,SSA)和BPNN模型结合后用于预测大宗商品价格(包括原油价格),证实了该混合模型的预测优越性(Wang et al.,2018)。而小波分解(Wavelet transform,WT)和多层BPNN模型结合,所得结果表明上述方法可以提升原油价格预测的准确性(Jammazi et al.,2012)。

众所周知,序列分解后得到的低频分量和高频分量能够呈现不同的特征。其中,高频分量表现出复杂性和不规则性,低频分量则表示序列中清晰的信息,因此恰当地处理非平稳成分能够有效提升原始序列的预测精度(Potts et al.,2016)。用EMD将原始序列分解成若干个IMF,再用小波包分解(Wavelet packet decomposition,WPD)对第一个子序列进行分解,结果表明处理高频序列能够提高模型整体的预测准确性(Yin et al.,2017)。然而,由于低频序列通常能够准确反映原油价格的变化规律和总体趋势,因此本文基于高频序列和低频序列的不同特征分别构建预测模型。

基于以上分析和认识,本文提出了一种新颖的VMD-LSTM-ELMAN国际原油价格预测模型。首先利用VMD技术将原始原油价格序列分解成若干子序列;然后采用ELMAN神经网络和LSTM分别预测最后一个高频分量和其余分量;最后将子序列的预测值求和作为模型最终的预测结果。以WTI原油期货和上海国际能源交易中心的原油期货日交易价格作为研究对象,本文的目的是回答以下两个问题：相较于其他对比模型,VMD-LSTM-ELMAN模型在处理非平稳和非线性特征时展现出了哪些独特的优势?VMD-LSTM-ELMAN模型在预测新兴市场和成熟市场原油价格时的表现有何不同?本文首先详细介绍基于国际原油价格的VMD-LSTM-ELMAN模型及预测效果评价方法;然后对实证结果进行分析与比较;最后提出本次研究的结论与对策建议。

1 研究方法

1.1 原油价格的VMD分解方法

引入变分模态过程对国际原油时间序列p(t)进行不同频率的分解,相关参数的更新步骤如下：首先,采用希伯特变换构造uk(t)的解析信号,以获得单侧频谱;其次,利用指数调谐确定uk(t)的频谱到相应基带;然后,计算解析信号梯度的平方L2范数,估计uk(t)的带宽,构建的约束变分问题为：

(1)

(2)

其中：K为模态个数,uk为极限K阶模态,δ(t)为Dirac分布,wk为中心频率,⊗为卷积算子。为了获得更优的分解结果,本文使用ADMM(Alternate Direction of multiplier)方法进一步改进分解过程,具体过程如下：

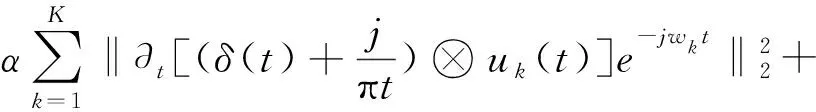
(3)

其中：α为二次惩罚因子,λ(t)为Lagrange乘子。

(4)

(5)

(6)

(7)

其中：ε为收敛精度,如果不满足公式(7)中的停止条件,n增加到n+1。至此,通过VMD的分解方法,将原油时间序列p(t)分解为从低频向高频排列且具有独立特征的N个IMF。

1.2 原油价格的预测方法

原油期货价格预测需要对训练数据构建合适的模型,建立序列的内在关系,进而为后续预测过程提供准确支撑。本文提出的VMD-LSTM-ELMAN预测模型主要设计步骤如下：

首先,对原始原油期货价格数据进行去除异常值与填补缺失值等数据预处理,之后采用VMD技术将复杂的原油期货价格分解成为N个代表不同频率成分的IMF,以降低原始序列的随机波动性,从而使后续的预测模型能够更准确地捕捉价格趋势和周期性成分。

其次,对分解得到的每个IMF进行归一化处理,确保其在相同的尺度上进行比较和分析。接下来,选择适当比例划分训练集与测试集,以便于模型的训练和性能验证。在本研究中,利用ELMAN神经网络预测最后一个高频分量IMFn,以处理高频序列不规则的特性;利用LSTM模型预测其余IMF,以处理包含长期趋势的信息。

最后,将N个利用ELMAN和LSTM模型预测后的IMF重构,以得到最终的预测序列。同时,基于损失函数MSE,MAE和MAPE,MDM统计检验及稳健性检验中评价本文提出的VMD-LSTM-ELMAN预测模型与对比模型的预测性能。

为了更直观地展示本文提出的VMD-LSTM-ELMAN模型的整体架构和各步骤之间的逻辑关系,本文将绘制的框架图展示在图1中,包括数据分解、模型训练和模型集成3个步骤,旨在提供清晰的视觉参考,有助于理解本文提出模型的工作机制和流程。

1.2.1 LSTM神经网络

LSTM神经网络的关键之处是其门控单元系统,它使网络能够有效地存储和处理历史信息。这种机制包括负责维持和更新历史数据状态的内部存储单元。LSTM神经网络通过使用不同的“门”(包括输入门、遗忘门和输出门)动态控制信息流,能够让网络有选择性地忘记历史信息或使用新信息更新单元状态。需要说明的是,在先前基于ANN模型的预测研究中,时间序列的特征通常需要事先计算并作为输入。与之相比,LSTM神经网络的优势在于其能够自动检测和提取对特定任务最有效的特征模式,因此适用于原油价格的预测。LSTM神经网络的结构及原理如图2所示。

图1 VMD-LSTM-ELMAN模型框架图Fig.1 Framework of the VMD-LSTM-ELMAN model

图2 LSTM神经网络单元图Fig.2 Diagram of an LSTM neural network cell

LSTM结构由记忆细胞、输入门、输出门和遗忘门组成,计算原理如下：

(1)输入门。记忆目前状态的信息,计算输入门it的值和在t时刻输入细胞的候选状态值at：

it=σ(Wi·(ht-1,Xt)+bi)

(8)

at=tanh(Wc·(ht-1,Xt)+bc)

(9)

其中：Wi,Wc代表相应的权重,bi与bc代表相应的偏置。

(2)遗忘门。控制遗忘的信息,计算在t时刻遗忘门的激活值ft：

ft=σ(Wf·(ht-1,Xt)+bf)

(10)

其中：Wf,bf分别表示遗忘门的权重和偏置,σ表示sigmoid函数。

(3)更新细胞状态。根据输入门和遗忘门的计算结果,对细胞状态进行更新,从而得出t时刻的细胞状态更新值Ct：

Ct=it·at+ft·Ct-1

(11)

(4)输出门。控制输出的信息,根据计算得到的细胞状态更新值Ct,从而得出输出门ot的计算公式：

ot=σ(Wo·(ht-1,Xt)+bo)

(12)

ht=ot·tanh(Ct)

(13)

其中：Wo和bo代表输出门的权重和偏置,ht为当前单元的输出值。

1.2.2 ELMAN神经网络

ELMAN神经网络是一种典型的全局前馈、局部递归网络模型,它由BP神经网络改进而来,在网络结构上具有相似之处。ELMAN神经网络由4个主要层组成：输入层、隐含层、连接层与输出层。输入层负责传递原油期货价格中的信息;隐含层通常采用非线性函数处理信息;连接层的作用是存储和记忆隐含层的输出,并将这些信息在下一时刻传回输入层,从而实现局部反馈;最后,输出层负责对信息进行线性加权处理。

由于连接层的引入,ELMAN神经网络能够记忆并处理过去的状态,使其适合于原油期货价格的时变特性,其结构如图3所示。

图3 ELMAN神经网络图Fig.3 Diagram of the ELMAN neural network

ELMAN神经网络的数学模型为：

(14)

其中：k为当前时刻状态,Y(k),X(k),u(k-1),Xc(k)分别为m维输出节点向量、n维中间层节点单元向量,r维输入向量和n维反馈状态向量,ω3,ω2,ω1分别为隐含层到输出层、输入层到隐含层、连接层到隐含层的连接权值,G(·)为输出神经元的传递函数,F(·)为隐含层神经元的传递函数,常采用sigmoid函数。

ELMAN神经网络采用误差平方和函数作为学习指标函数。

(15)

1.3 预测性能的评价指标

首先本文采用均方根误差(Mean square error,MSE)、平均绝对误差(Mean average error,MAE)和平均绝对百分比误差(Mean absolute percentage error,MAPE)为标准,对VMD-LSTM-ELMAN模型的性能进行评估,具体公式如下：

(16)

(17)

(18)

其中：dt为原油期货实际价格,yt为预测价格,N表示样本个数。采用MSE,MAE和MAPE标准来评估实际价格与预测价格的偏差,其数值越小,表明模型的预测性能越优异。不仅如此,本文还通过构建线性回归方程Y=aX+b(其中Y和X分别代表原油期货实际价格和预测价格)来进一步解释预测模型的性能。在这一方程中,斜率a、截距b和决定系数R2(R-square,R2)起到关键作用。具体地,R2的定义如式(19)所示：

(19)

(20)

Lossi=L(ft,fit)=L(eit)i=1,2

(21)

dt=L(e1t)-L(e2t)t=1,2,…,T

(22)

H0：E(dt)=0t=1,2,…,T

(23)

其中：Lossi为第i个模型的损失函数,dt为损失微分级数,T为测试集长度。将真实值与预测值之间的损失函数简化为{L(eit),i=1,2},即{L(ft,fit)=L(eit),i=1,2}。原假设H0表示模型间具有相同的预测性能。为了预测长记忆序列,定义ω2表示为dt的长记忆方差,MDM统计量的表达如下式：

(24)

(25)

(26)

2 实证结果与分析

2.1 数据样本与分析

由于WTI原油和国内原油分别在北美和中国能源市场占据重要地位,因此本文选取纽约商品交易所交易的WTI原油期货价格与上海国际能源交易中心交易的原油期货价格的日交易价格为研究对象。WTI原油期货价格选自2000年1月4日至2021年9月30日的5 555个数据(数据来源于美国 U.S Energy Information Administration);国内原油期货价格选择2018年3月26日至2021年9月30日共858个数据(数据来源于东方财富choice),其中前90%的数据为训练集,后10%的数据为测试集。图4展示了WTI和国内原油期货序列的走势。

原油期货价格序列及其IMF的描述性统计如表1所示,虽然两种原油序列的偏度方向不同,但仍呈现出明显的有偏胖尾特征。J-B统计量证明在1%显著性水平下,两种原油期货价格及其IMF均拒绝正态假设的零假设,表明序列都不服从正态分布。本研究进行Ljung-Box检验时选择了10个滞后期,旨在实现对时间序列自相关特性的有效检测,同时避免由于过多的滞后期而导致数据过拟合问题。值得注意的是,L-B(10)统计量在1%显著性水平下中拒绝第10阶无自相关的零假设,不仅支持了本文对滞后期选择的合理性,而且还进一步证明了原油期货价格信息具有长记忆性的特征。

为减少原油期货价格数据中噪声对训练过程产生的影响,本文采用0—1归一化对序列进行预处理：

(27)

其中：minxt,maxxt分别为原油期货价格的最小值与最大值,接下来通过公式(28)反归一化出测试集的最终预测值：

(28)

2.2 分解结果

VMD的分解效果受模态个数的限制具有不稳定性,如果K值较小,容易导致序列分解不充分;如果K值较大,则会出现模态混频的缺点。因此本文采用观测中心频率的方法预设K值。不同K值下IMF对应的中心频率如表2所示,可以发现当K预设为[1,10]时,WTI和国内原油期货中IMF10的中心频率最大值分别为0.470 4与0.468 2,中心频率最小值分别为2.28×10-5和1.43×10-5,趋于稳定。因此,本文将WTI和国内原油期货的最佳模态个数设置为10,分解结果见图5。

图4 原油价格序列图Fig.4 Diagram of crude oil prices

表1 原油价格及其子序列的描述性统计分析Table 1 Descriptive statistical analysis of the crude oil prices and different subseries

表2 不同K值下IMF的中心频率Table 2 Central frequency of the IMF under different K values

图5 原油价格分解图Fig.5 Decomposition graph of crude oil prices

以上分析表明,由于多种驱动的耦合,原油价格呈现出多种多样的特征,具体表现在高频和低频分量之间的特性。具体而言,一方面,原油市场作为一种商品市场,其价格的波动在短期内容易受到内部市场机制(如供求机制和风险机制)的影响,因此对原油期货价格的长期趋势影响较小;另一方面,非市场因素,即原油市场的外部环境因素(如政策调整、经济危机和政治形势变化)成为导致原油价格长期波动的原因。

2.3 预测结果

本研究采用VMD-LSTM-ELMAN作为预测模型,并纳入SVR,ELM,MLP,LSTM,ELAMN,VMD-SVR,VMD-ELM,VMD-MLP,VMD-LSTM和VMD-ELMAN进行比较。其中组合预测模型的参数选择采用试错法,具体结果见表3。可以看出,LSTM结构的第一层为具有128个神经元的LSTM层,结构第二层为64个神经元的LSTM层,最后一层为全连接层,学习率为0.01,各层的激活函数均采用修正线性单元(Rectified linear unit,ReLU)。ELMAN神经网络由输入层、包含16个单元的隐含层、连接层和输出层构成,误差容限设置为0.000 5,且LSTM与ELMAN神经网络的窗口大小都设置为5。

基于上述参数选择结果,本文构建LSTM和ELMAN神经网络预测模型,并开展实证分析。

表3 预测模型的参数选择Table 3 Parameter selection for the prediction models

采用损失函数MSE,MAE和MAPE评价模型对原油期货价格的预测准确性,在数值上更具说服力,结果见表4。VMD-LSTM-ELMAN模型的MSE,MAE和MAPE值均小于其他对比模型(包括单一模型和使用相同预测技术的分解集成模型),WTI原油价格的MSE,MAE和MAPE值分别为1.513 6,1.063 7和0.023 2,国内原油价格的MSE,MAE和MAPE值分别为6.841 2,2.000 1,0.004 4。为了更直观地展示这些结果,本文绘制了雷达图来比较不同模型在WTI原油价格和国内原油价格预测中的MSE,MAE和MAPE值。图6-A,B,C分别表示模型在同一损失函数下,对WTI与国内原油数据集的预测表现。具体而言,图中每个轴代表一个预测模型,而轴的长度代表损失函数的大小。由此可见,雷达图清晰地展示了VMD-LSTM-ELMAN模型在这些关键指标上的优势,从而证明了其在原油期货价格预测中的有效性。

表4 三种损失函数下原油价格的预测评价结果Table 4 Forecasting evaluation results of crude oil prices under three loss functions

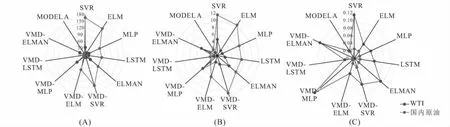
图6 原油价格预测模型性能雷达图Fig.6 Radar chart of the crude oil price forecasting model performance

与此同时,为进一步比较VMD-LSTM-ELMAN模型与对比模型的预测性能,本文基于MSE,MAE和MAPE损失函数进行MDM检验,结果见表5。对于WTI原油期货价格,30种检验中存在27种表明原油期货价格的损失函数在1%显著性水平下拒绝原假设;对于国内原油价格,所有损失函数都在1%显著性水平下拒绝原假设。结果表明,本文所提出的VMD-LSTM-ELMAN模型与其他相关模型的误差具有统计学显著性,这也表明VMD-LSTM-ELMAN模型预测能力优于其他模型。

除了利用MSE,MAE,MAPE和MDM检验评价模型的预测准确性之外,本文进一步采用线性回归方法分析不同模型的预测能力,参数结果见表6。在VMD-LSTM-ELMAN模型的线性回归结果中,WTI和国内原油期货价格的斜率a分别为0.980 3和0.938 9,几乎趋近于1,截距b分别为0.016 2和25.550 0,相较于对比模型更加趋近于0。另外,VMD-LSTM-ELMAN模型的R2计算结果分别为0.997 9和0.994 9,几乎接近1。上述分析均表明VMD-LSTM-ELMAN模型是一种高准确性的原油期货价格预测方法。

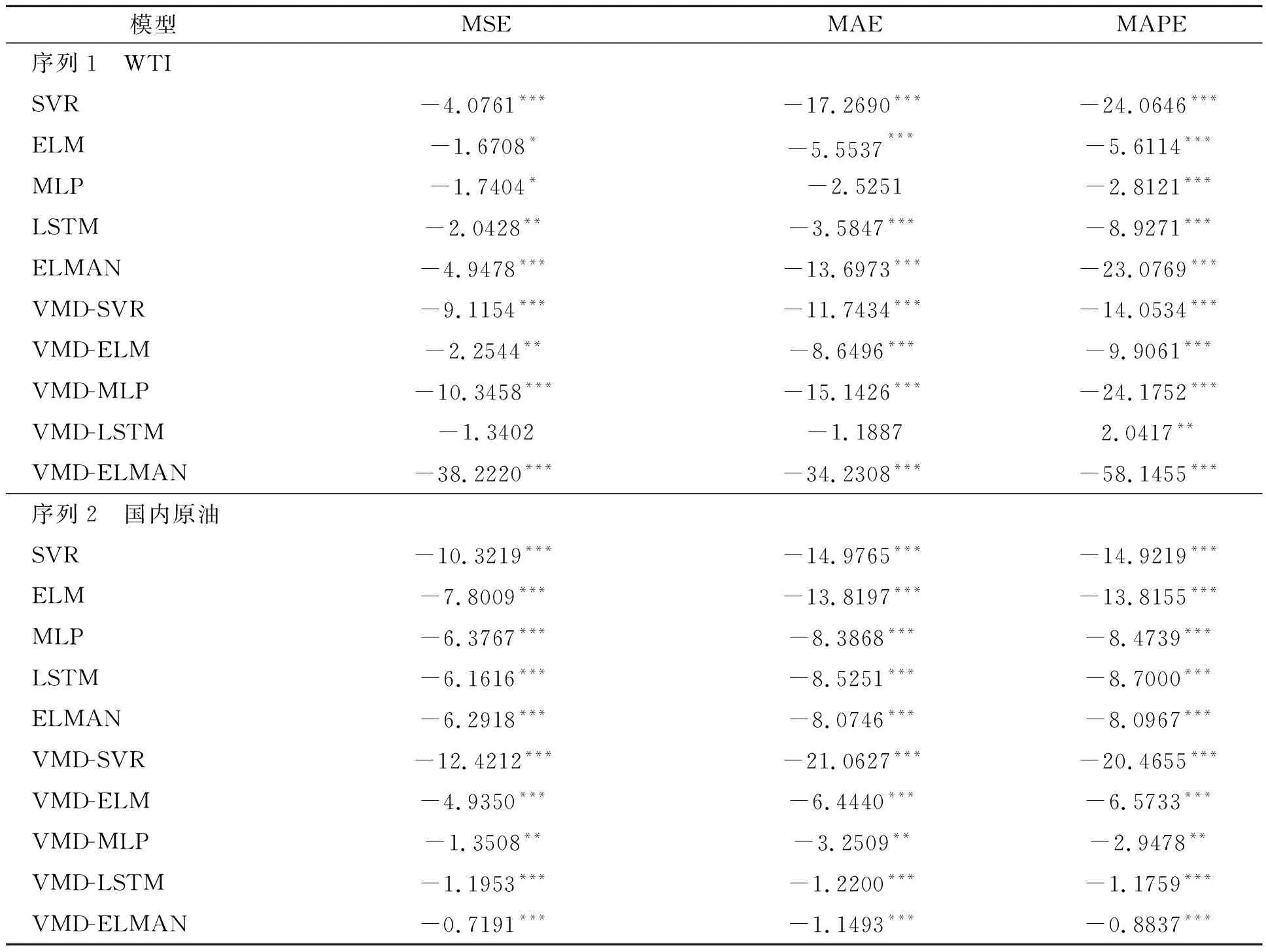
表5 三种损失函数下MDM检验结果Table 5 MDM test results under three loss functions

表6 不同模型的线性回归结果Table 6 Linear regression results for the different models

为了更加直观地比较各个模型的预测效果,本文将原始原油期货价格序列真实值与不同模型的预测值绘制在图7中。可以发现,代表原始序列的蓝色粗线与代表VMD-LSTM-ELMAN模型预测值的红色粗线举例最接近,由此可见VMD-LSTM-ELMAN模型相较于其他对比模型具有更优秀的拟合程度。

综上所述,无论是通过模型预测值曲线相近程度,还是基于MSE,MAE,MAPE与R2值进行比较分析,实证结果均表明相较于SVR,ELM,MLP,LSTM,ELAMN,VMD-SVR,VMD-ELM,VMD-MLP,VMD-LSTM和VMD-ELMAN模型,本文采用的VMD-LSTM-ELMAN模型在预测原油期货价格上具有更高的预测精度与适用性。

图7 不同模型的预测结果对比图 Fig.7 Comparison of the prediction results from different models

2.4 稳健性检验

为证明VMD-LSTM-ELMAN模型的稳健性,本节选取前60%的序列作为训练集,后40%的序列作为测试集。该数据划分比例旨在实现两个关键目标：首先,通过保留足够多的数据作为训练集,以确保模型具有充分的数据来学习和捕捉原油时间序列的关键特征和动态。其次,将40%的数据保留作为测试集,可以在不同的数据子集上验证模型的预测能力,这有助于评估模型在实际应用中的泛化能力和稳健性。通过这种方式,可以进一步探索在不同训练集和测试集长度下模型的预测性能。具体的实验结果展示在表7中。

WTI原油价格的MSE、MAE和MAPE值分别为3.104 1,1.470 5和0.025 6,国内原油价格的MSE,MAE和MAPE值分别为51.166 7,6.792 4和0.019 4,表明VMD-LSTM-ELMAN模型在MSE,MAE和MAPE损失函数的计算结果上仍然优于其他对比模型。

表7 三种损失函数下原油价格的预测评价结果Table 7 Forecasting evaluation results of crude oil prices under three loss functions

测试集中的MDM检验结果如表8所示。对于WTI原油期货价格,所有损失函数都在1%显著性水平下拒绝原假设;对于国内原油价格,30种检验中存在28种表明原油期货价格的损失函数在1%显著性水平下拒绝原假设。结果同样表明VMD-LSTM-ELMAN模型的预测优势是显而易见的。

表8 三种损失函数下MDM检验结果Table 8 MDM test results under three loss functions

线性回归参数结果如表9所示。从表中可知,WTI和国内原油期货价格的斜率a分别为0.966 3和0.982 1,几乎趋近于1;截距b分别为2.998 0和-0.508 7,几乎趋近于0;R2值分别为0.995 7和0.999 4,几乎接近1,表明本文采用的VMD-LSTM-ELMAN模型适用于原油期货价格序列的预测,并且较对比模型具有明显的优势。

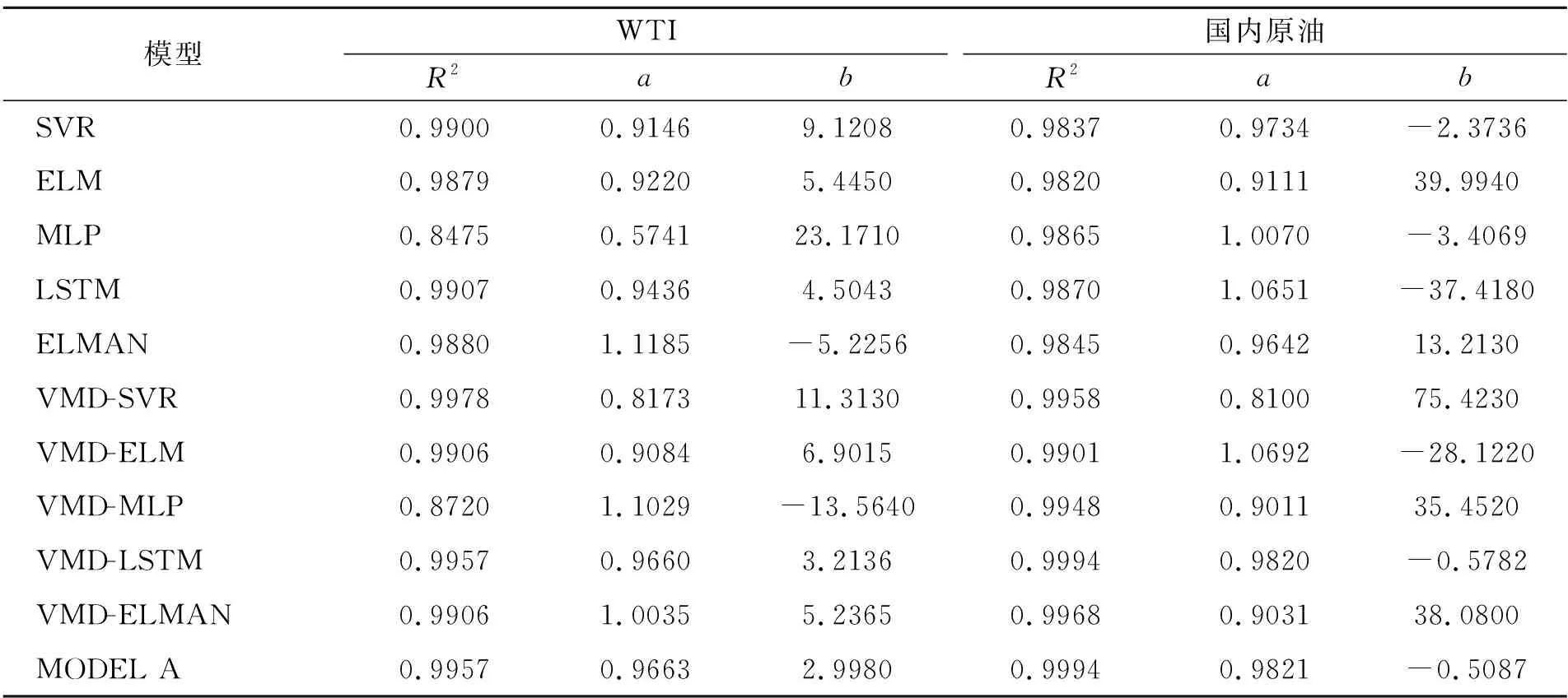
表9 不同模型的线性回归结果Table 9 Linear regression results of the different models

除此之外,鉴于Brent原油作为全球原油市场中最主要的基准之一,本文采用相同样本区间的Brent原油价格作为替代指标,以代替先前使用的WTI原油价格,从而进一步验证本文提出的VMD-LSTM-ELMAN模型在不同原油市场环境下的泛化能力。

在进行这一调整后,本文使用与WTI原油相同的方法论和参数设置,以确保结果具有可比性。测试集中的MDM检验结果如表10所示。对于Brent原油期货价格,30种检验中有27种检验的结果在1%显著性水平下拒绝原假设,进一步凸显了VMD-LSTM-ELMAN模型在预测原油价格方面的显著优势,不仅增强了VMD-LSTM-ELMAN模型在不同原油市场条件下的可信度,也为未来在其他原油市场的应用奠定了基础。

表10 三种损失函数下MDM检验结果(Brent原油)Table 10 MDM test results under three loss functions (Brent crude oil)

综上所述,本研究在稳健性检验环节中对数据集进行了多样化的调整,包括改变数据划分比例和使用不同的数据集。实证研究结果一致表明,本文采用的VMD-LSTM-ELMAN模型表现均优于其他对比模型,不仅凸显了该模型在处理多变数据时的适应能力,也证实了其在面对不同市场情况和数据特性时的出色稳健性。

3 结论及对策建议

原油期货价格的波动会影响人们的生活,甚至阻碍国民经济的发展,因此提升原油期货价格预测的准确性在全球金融市场中具有举足轻重的作用。本研究的主要贡献是结合数据分解方法和人工智能预测模型,建立一种新型原油期货价格混合预测模型,以实现更准确的原油期货价格预测。本文主要从以下三方面集中对WTI原油期货价格和国内原油期货价格进行实证分析：(1)相较于其他单一模型和使用相同预测技术的分解集成模型,VMD-LSTM-ELMAN模型对于WTI原油价格和国内原油价格预测的MSE,MAE和MAPE值分别为(1.513 6,6.841 2),(1.513 6,2.000 1)和(0.023 2,0.004 4),WTI和国内原油期货价格预测值的R2值分别达到了0.997 9和0.994 9。上述损失函数的值在所有模型中最小,且R2值最接近于1,凸显出VMD-LSTM-ELMAN方法的良好性能。(2)进一步地采用线性回归分析来验证模型的适用性。分析结果显示,WTI原油和国内原油数据集的斜率a和截距b分别为(0.980 3,0.016 2)和(0.938 9,25.550 0),趋近于1和0,表明本文采用的模型适用于原油期货价格序列的预测。(3)本文还引入MDM检验以比较VMD-LSTM-ELMAN模型与其他模型在预测能力方面的差异。检验结果表明,在大多数情况下,两类原油市场期货价格的损失函数在1%显著性水平下拒绝原假设,证明了VMD-LSTM-ELMAN模型比其他模型具有更强的预测能力。最后,本文通过稳健性检验再次验证了VMD-LSTM-ELMAN模型在不同训练集长度下和不同原油市场的预测优越性。

基于以上结论,利用VMD-LSTM-ELMAN模型准确预测原油期货价格不仅有利于个体参与者和相应公司规避关联交易风险,而且有利于政府部门对原油相关产品的贸易进行监管和宏观调控。综上所述,本文进一步为政府部门制定政策、减少环境污染以及调整世界经济格局等方面提供了思路。