城市地面塌陷灾害风险评估研究

余满仓，吕敦玉，孟舒然，张建羽，刘松波，王翠玲

（1.中国地质科学院水文地质环境地质研究所，河北石家庄 050061；2.中国地质大学（武汉）工程学院，湖北武汉 430074；3.中国地质调查局第四纪年代学与水文环境演变重点实验室，河北石家庄 050061）

0 引言

随着城市化进程的加快和地下空间资源的开发利用，地质环境愈发脆弱，严重制约了城市的安全和可持续性发展（吕敦玉等，2015；曾灿军和陈卫忠，2018；易荣和贾开国，2020；葛伟亚等，2021）。近年来，全国城市路面塌陷进入了爆发期，范围遍及全国各地大小省市（许晓莹和陈斌，2021），尤为典型的事故有：2018年2月7日，佛山禅城路面塌陷事故，造成11人死亡；2020年1月13西宁塌陷事故，造成17人受伤；2021年5月西安地下通道塌陷事故，造成1人死亡。可见，地面塌陷的发生，对人民生命安全、生态环境和经济发展产生了巨大威胁。地面塌陷，是指在人为因素或者自然因素影响下，地表岩土体整体失稳向下陷落并形成塌陷坑的现象。由于其突发性的特点，这就决定了地面塌陷是很难预测和防治的（黎兵，2022；仙永凯和史婧，2022）。因此，对城市地面塌陷展开机理调查和风险评估工作尤为重要。

目前，国内外对于城市地面塌陷的机理研究已取得较多成果，主要集中在案例统计、理论分析、模型试验、数值模拟等方面（蓝雄东，2023）。钟世英和丛波日（2016）通过调查资料，对2014～2015年全国范围内的66起地面塌陷进行了统计分析，按机理把地面塌陷分为潜蚀型塌陷、冲爆型塌陷、真空吸蚀型塌陷、松散土体型塌陷4类。赵延林等（2010）建立了基于突变理论的强度折减法，这为采空区重叠顶板稳定性的研究提供了一种新的判据。Ali and Choi（2020）通过建立物理模型，分析了不同土壤剖面、水流类型和渗漏位置对土洞的影响，并认为土层类型是塌陷发生的关键因素，而后建立回归模型验证了实验结果，并以此来预测地面塌陷发生的风险水平。Jung et al.（2023）等在研究管道破损诱发地面塌陷时采用数值模拟的方法建立了水土耦合模型，分析了重复性强降水对空洞扩张的影响，进而提出了切实可行的监测策略。对塌陷机理研究透彻之后，其目的就是进一步对风险做出科学评估和预防，在这方面国内外学者也做了很多工作。然而，不同学者在开展研究时往往自成体系，评估指标选取、定制也存在较大个体差异（陈希和陈正，2023a）。对于具体的地面塌陷风险评价工作而言，多属性决策是一种主流方法，目前国内外都将权重的确定作为灾害评价工作的重点，因为权重的精度直接决定评价模型的合理性和实用性（周子勇等，2023）。在塌陷灾害的评价中，由于致灾因子的复杂性，人们对于指标因子权重的设置都是主观设定，常用的方法有主观经验法、专家调查法等（张必昌等，2019）。如叶远春和宋谷长（2012）调查了大量北京市地面塌陷事故，运用风险控制理论，结合德尔菲法、层次分析法，建立了一套城市道路空洞风险可能性和后果的评估体系。张昌新等（2014）以深圳地铁某线的地面塌陷风险为例，选取了导致地面塌陷的主要主要因素作为影响指标，用半定量法对其进行了风险评估。

基于上述研究，目前存在的方法大多是通过专家经验、主观评价来确定权重，评价结果受主观因素影响严重，存在一定局限性。因此，本文在对郑州市大量地面塌陷案例调查基础上，建立塌陷风险发生可能性指标体系，尝试把层次-熵权-灰色关联法应用于复杂成因下的城市地面塌陷评价中，来解决主客观权重分布不均问题，并验证赋权结果的准确性，以此获得一种能够面向实际应用的城市地面塌陷评估方法。

1 城市地面塌陷风险评估

1.1 风险发生可能性指标选取

城市地面塌陷突发灾害是水文地质、工程地质活动和人类工程作用综合产物，其形成具有明显的时空突发性、随机分布的特点（白凌燕等，2011），其规模变化、空间分布受多重因素的制约。根据相关资料调研，对郑州近年来105处地面塌陷诱发因子进行了统计分析，这些数据涵盖了道路塌陷、基坑塌陷、小区地面等不同的位置范围，因此更具有代表性，事故诱发原因占比如图1所示。可见，地下管线破损渗漏、周边地下施工扰动、降水入渗可能是引发郑州城市地面塌陷的主要因素。

图1 不同致灾原因占比图Fig.1 Proportion chart of different causes of disasters

风险评估是在对风险基本了解的基础上，综合运用相关风险评估专业理论和工程经验，对事故发生的可能性进行研究。通过以上调研，并结合国内流行的《城市地下病害体综合探测与风险评估技术标准》①和专家学者对地面塌陷原因和机理的分析（万志清等，2003；侯超群，2018），本文从管线因素、病害体因素和环境因素中选取一定的评价指标来建立地面塌陷风险发生可能性评价体系（陈希和陈正，2023b），并将评分标定，见表1。

1.2 风险发生可能性指标权重计算

1.2.1 层次分析法

（1）层次分析法原理及步骤

层次分析（AHP）是用系统化、层次化的决策方法来解决无法定量描述的问题，其具体思路是将工程问题分解成不同层级且具有隶属关系的目标与字母表，之后构建判断矩阵且依据经验比较确定层级结构中各目标的重要性，最后求出方案层各个因素相对于总目标层的相对重要权重（Saaty，1987）。具体步骤如下：

①构建层次模型。深入分析所要解决的实际工程问题，确定系统层级结构和各层下指标因素，逐一分层，且层级内指标各自独立。

②构建判断矩阵。将每一层级中第i个元素与第j个元素相对于上一层及重要程度两两对比，并依据1～9标度法表示其重要程度，如表2。

表2 对比分析标度及含义Table 2 Comparative analysis scales and meanings

③各因素指标权重计算并做一致性检验。计算各因素指标权重常用的方法有方根法和和积法，本次拟采用方根法，求解如下。

a.求解判断矩阵的特征向量

b.特征向量的归一化处理

c.计算判断矩阵的最大特征根

d.判断矩阵的一致性检验：

第一步，求解判断矩阵的偏离一致性指标CI=

第二步，根据判断矩阵阶数n选取平均随机一致性指标RI，如下表（表3）（许树柏，1988）。

表3 平均随机一致性指标Table 3 Mean randomized consistency indicators

第三步，求解判断矩阵的一致性比率CR=当CR＜0.1时，认为判断矩阵满足一致性检验，若CR＞0.1时，判断矩阵不满足一致性检验。

（2）层次分析法指标权重计算结果

针对上文对郑州市城市地面塌陷风险因素识别的基础上，并咨询专家比较不同因素指标之间的重要性，从管线因素、病害体因素和环境因三个方面素分析计算权重。地面塌陷（A）为目标层，其中评价体系包括管线因素（B1）、病害体因素（B2）、环境因素（B3），称为准则层。管线因素（B1）包括管线类型（C11）、管线脆弱性（C12）、服役年限（C13）、管线埋设方式（C14）、管线直径（C15）；病害体因素（B2）包括地下病害体跨径（C21）、病害体上覆土层厚度（C22）；环境因素（B3）包括岩土条件（C31）、道路现状（C32）、施工干扰（C33）、水环境条件（C34）、地表荷载（C35）。城市地面塌陷可能性风险评价层次递阶结构模型如下图2所示。

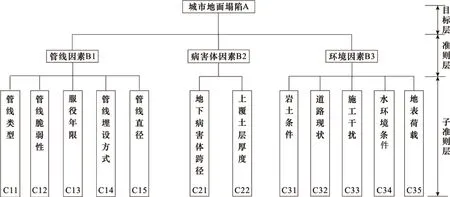
图2 地面塌陷风险评价层次递阶结构模型图Fig.2 Hierarchical structure model for ground collapse risk evaluation

①准则层B对目标层A的权重计算及一致性检 验（表4）

表4 城市地面塌陷可能性风险评价指标各权重情况及检验结果Table 4 Weights and test results of the indicators for evaluating the risk of urban ground collapse possibility

②子准则层Cii对准则层Bi的权重计算及一致性检验

以管线因素指标权重计算为例，见下表（表5）。同理，可计算病害体因素和环境因素，此处不再赘述。

表5 管线因素指标权重计算及检验结果Table 5 Calculation of pipeline factor indicator weights and test results

③复合权重（表6）

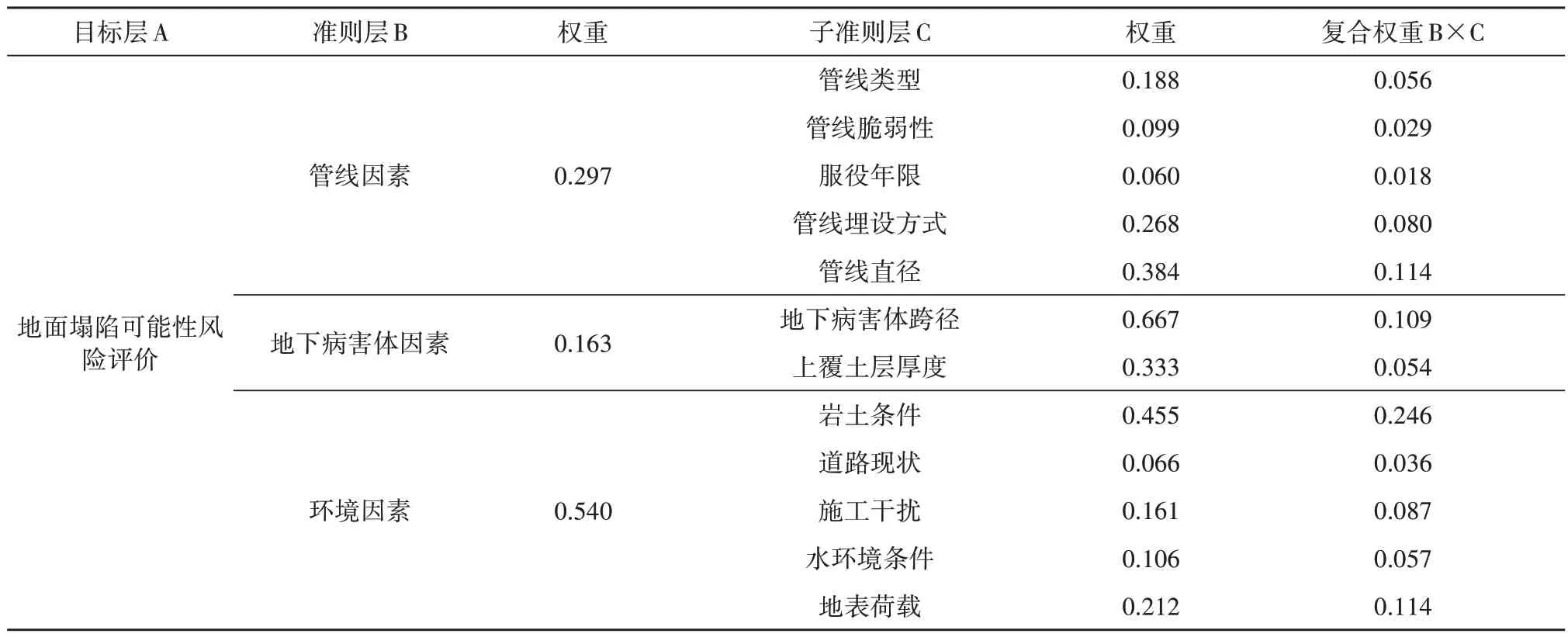
表6 城市地面塌陷风险评价组合权重-层次分析法Table 6 Weights of urban ground collapse risk evaluation combinations - hierarchical analysis method

1.2.2 熵权法

（1）熵权法原理及步骤

熵权法是依据信息熵来判断指标离散程度的一种决策方法，其在分析指标信息分布规律和指标关系基础上，对权重进行客观评估（杨木易，2023）。通常信息熵值越小，指标离散程度越大，该指标对评价的影响即权重就越大。具体求解步骤如下：

①通过查找资料或咨询专家建立各评价指标的判断矩阵

②归一化处理以消除指标量纲不同或负值指标产生的影响

正向指标归一化：

负向指标归一化：

③确定指标在评价对象中的比重

④计算指标熵值

⑤计算指标差异度

⑥确定各指标权重

（2）熵权法指标权重计算结果

熵权法的优势就是能较为准确的反映客观事，此处定性指标以上文层次分析法中专家打分构建的判断矩阵为准，结果如下（表7）。

表7 城市地面塌陷风险评价组合权重-熵权法Table 7 Weights of urban ground collapse risk evaluation combinations - entropy weight method

1.2.3 组合赋权

在传统的城市地面塌陷可能性风险评价中，决策人员和专家打分往往对评价结果起着重要作用，即单一的层次分析法主观性较强，导致评价结果往往与客观事实有较大冲突（孙晓永，2020；Grošelj and Zadnik，2018）。熵权法虽然能减少主观性对决策结果的影响，但对于指标间的组合效应缺乏考虑，仍存在一定局限性。为了充分考虑专家经验和客观环境的影响，结合层次分析法和熵权法综合赋权以期得到良好的评价结果。

在确定评价指标主观权重和客观权重后，由于评价指标个数较多，采用乘数归一法计算综合权重（李刚等，2017），计算公式为：

其中，wi为层次分析法所计算各指标权重；vi是熵权法所计算各指标权重。依据经验，α取0.5。计算结果如下（表8）：

表8 城市地面塌陷风险因子权重Table 8 Urban ground collapse risk factor weights

最后，对层次分析法（主观权重）、熵权法（客观权重）以及组合权重结果进行分析比较，结果如图3所示。

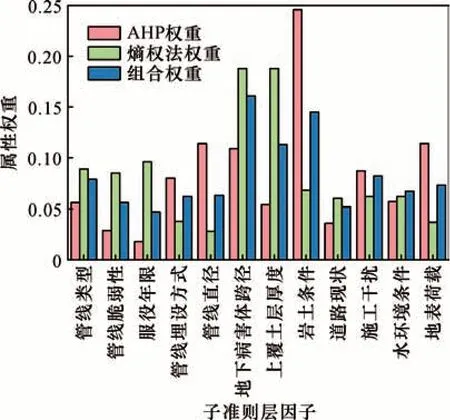
图3 权重结果对比图Fig.3 Comparison of weight results

由权重结果分布图可知，层次分析法受到判断水平和个人偏好等主观因素的影响，在很大程度上突出了岩土条件的重要性，部分学者通过调查认为不良地质条件是诱发地面塌陷的主要因素，因而具有一定的合理性。熵权法主要依靠较强的数学理论，计算结果显示地下病害体跨径和上覆土层厚度是影响地面塌陷的主导因素，这是由于病害体因素是地面塌陷产生的先决条件。尽管熵权法在一定程度上避免了主观因素的干扰，但是缺乏决策者的意愿，因此二者均存在一定局限性，使得赋权结果也呈现较大差异。本文提出的主客观结合的方法能充分体现二者的优越性，克服单一赋权法的不足，使赋权结果更具有权威性。另外，Jiang et al.（2023）通过卷积神经网络（CNN）对影响城市地面塌陷的众多因素也做了相关分析，其认为施工规模（占比：0.144）和施工现场的距离（占比：0.132）是导致道路坍塌的最显著因素；陈希和陈正（2023a）利用线性加权主客观权重的方法得到管线因素占据最大比重；冉星星（2023）利用机器学习的方法研究得出深圳市域中地面塌陷灾害风险贡献率最大的是基坑施工密度，均与本文结果存在一定差异。尽管如此，由于学者们对指标体系选取和权重确定方法不一致，结果不同也无可厚非，都存在一定的合理性，但AHP-熵权法组合赋权具有更强的可操作性，为城市地面塌陷防治起到了积极的指导作用。

1.3 风险发生可能性评估模型

在2.1中已经对城市地面塌陷风险指标进行了总结，并通过专家评分的方法对各指标进行了量化处理，具体标准如表1所示。

依据城市地面塌陷隐患风险发生的可能性指标量化标准以及上文运用层次分析法和熵权法组合赋权得到的各个评价指标权重，采用有序加权法计算风险发生的可能性分值P，如式（11）所示。

式中：P——地面塌陷风险发生可能性分值；

K——风险系数，通常取1.0，发生地质灾害等偶然因素影响或道路长期未开展养护时，可取1.1～1.2（陈希和陈正，2023a）；

P1——管线因素分值；

P2——地下病害体因素分值；

P3——环境因素分值；

WA——管线因素权重；

WB——地下病害体因素权重；

WC——环境因素权重。

其中Pi分值算法以地下管线P1分值算法为例，按下式计算。

式中：P11——地下管线类型分值；

P12——管线脆弱性分值；

P13——管线服役年限分值；

P14——管线埋设方式分值；

P15——管线直径；

WA1——地下管线类型权重；

W12——管线脆弱性权重；

W13——管线服役年限权重；

W14——管线埋设方式权重；

W15——管线权重。

根据计算得到的可能性分值，结合现场状况，将城市地面塌陷可能性风险等级分为以下五级，见下表（表9）。

表9 城市地面塌陷风险发生可能性等级划分Table 9 Classification of the likelihood of occurrence of urban ground collapse risk

2 典型评价指标的灵敏度分析

上文通过案例调研和专家经验列举了城市地面塌陷风险发生可能性评价指标，并以主客观结合的方法计算出了各风险指标的权重。为了验证结果的有效性，本文运用FLAC 3D数值模拟软件模型，研究典型指标对地面塌陷的不同影响程度，其中主要涉及地下空洞尺寸（包括地下空洞跨径和上覆土层厚度）、力学性质（包括内摩擦角和杨氏模量）、路面荷载三个方面。现基于数值模拟结果，采用灰色关联法对风险指标灵敏度进行分析计算。

2.1 数值模拟分析

2.1.1 有限元模型构建

采用“Rhion 6.0”软件建立模型并划分网格，主要通过点、线、面、体，建立所研究对象的几何形态，再运用软件内部的网格划分功能，然后通过一定的接口程序导出适用于 FLAC 3D 的网格节点和单元信息，导入 FLAC3D 之后即可得到所研究对象的网格模型。尺寸为30 m×30 m×30 m，节点数量为25806个，共建立了142883个单元空间，此处为了使计算结果更符合实际，调整为较小的网格尺寸。文献显示，地下空洞形状多为椭球形（王帅超，2017），在空洞未挖除之前获得该地的初始应力，然后挖出空洞并在侧面和底部设置零位移边界进行模拟。另外在进行的模拟计算中，沥青路面结构层以往在分析其应力、应变和位移关系时，通常采用弹性层状体系。而对地层土体采用弹塑性理论计算，强度准测采用摩尔库伦模型（Lee et al.，2018）。构建模型如下（图4）：

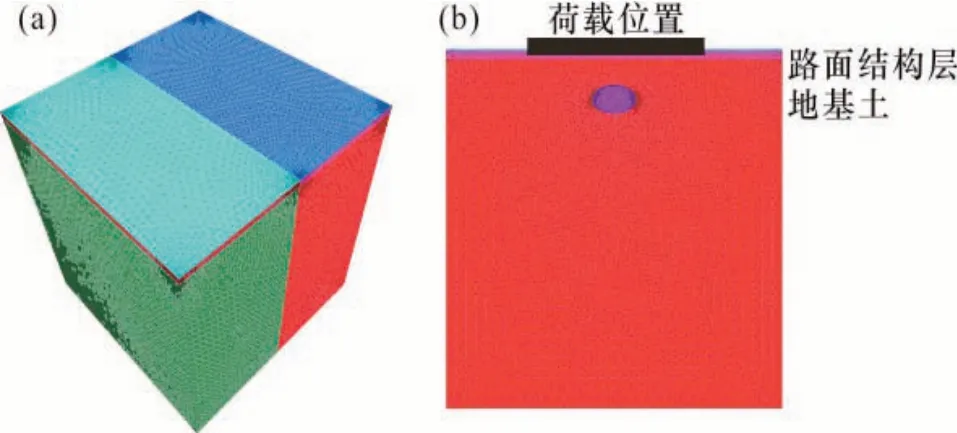
图4 模型示意图Fig.4 Model schematic diagrams

为研究典型指标对地面塌陷的不同影响程度，由此随机建立6个模型，各模型空洞几何尺寸和路面荷载及路面结构层下土体参数如下（表10）：

表10 地下空洞几何尺寸、路面荷载和地层土体参数取值Table 10 Underground cavity geometry， pavement loading and ground soil parameter values taken

城市路面结构一般为沥青路面，其中包括面层和基层②，此处以郑州市路面材料参数为准，见下表（表11）。

表11 路面材料参数Table 11 Pavement material parameters

2.1.2 数值模拟结果分析

通过FLAC 3D数值模拟软件计算，各模型沉降位移云图如图5所示。可见，在空洞正上方产生的路面沉降位移最大，向两侧沉降量逐渐以扇形形式展开，逐步减小；空洞下方土体受影响较小，且随着距离的增加，沉降逐渐缩小，直至稳定。

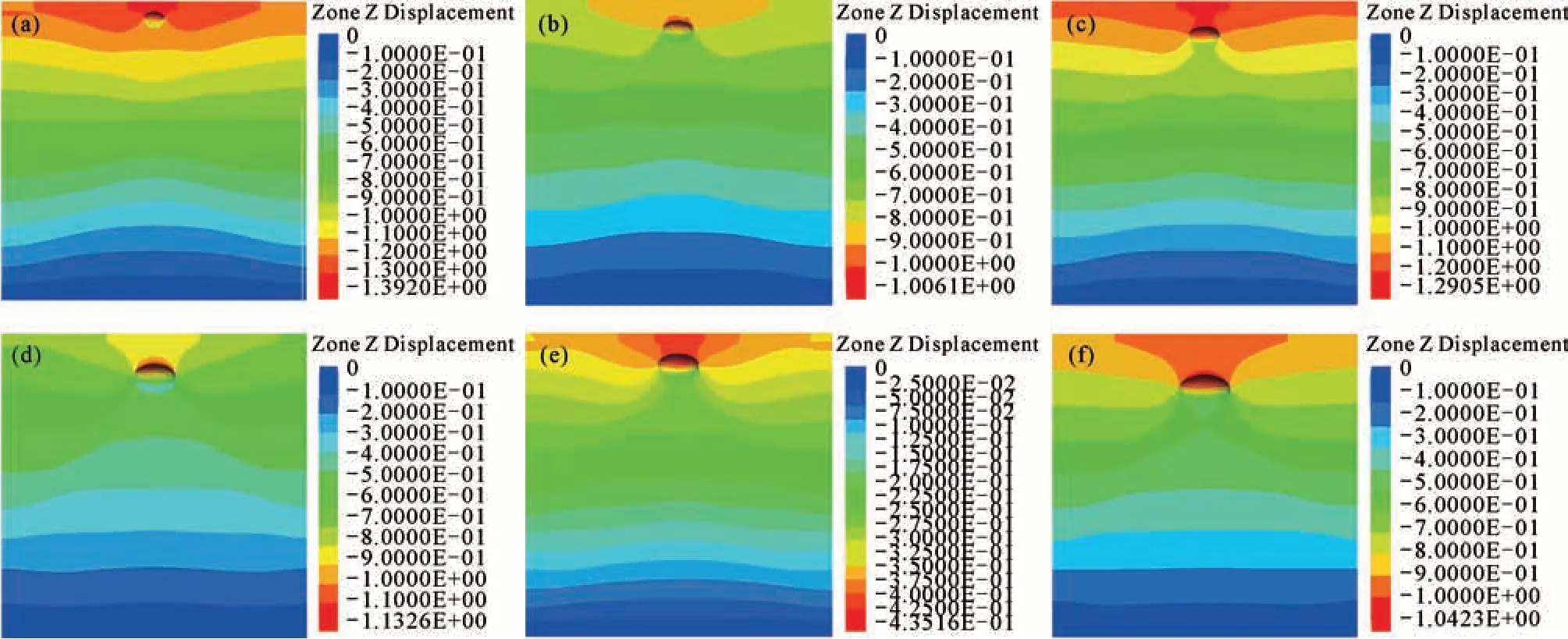
图5 沉降位移云图Fig.5 Settlement displacement cloud map

2.2 基于灰色关联法的灵敏度分析

2.2.1 灰色关联法原理及计算步骤

灰色关联度法是灰色系统分析方法中一项重要内容，其运用“曲线相似程度判断关系”的原理，通过样本数据来衡量因素之间发展趋势的相似或相异程度，非常适合动态历程分析。如果曲线越接近，则证明比较序列和参考序列之间相关程度越高，反之，相关性越低。灰色系统关联分析的具体计算步骤如下：

（1）确定反应系统特征的参考数列和分析数列

参考序列：

分析序列：

x’m={x’

m(1)、x’

m(2)、x’

m(3)...x’m(n)}，m表示序列个数。

（2）对参考数列和比较数列即母序列和子序列进行无量纲化处理，常见的无量纲化处理方法有四种，即：①初值化方法；②均值化方法；③区间值化方法；④倒数化方法（崔孝飞，2019）。

（3）计算关联系数

关联系数：

其中，ρ为分辨系数，一般取0.5；

Δij= |xi(j)-x0(j)|，x0(j)、xi(j)为消除量纲后的母序列和子序列；

（4）计算关联度

以平均值来展现不同序列因素之间的相对变化情况，即

2.2.2 灵敏度计算

以数值模拟结果为依据，选取城市地面塌陷引起的路面最大沉降位移作为参考序列：x’0=选取各相关影响地面塌陷的典型因子作为分析序列，即子序列x’m。令地下空洞跨径为x’1、上覆土层厚度为x’2、内摩擦角为x’3、杨氏模量为x’4、路面荷载为x’5，取值见表12。采用初值化方法进行无量纲处理后根据式（14）计算关联度，结果见表13和14。

表12 母序列 x’0和子序列 x’iTable 12 Parent sequence x’0 and subsequence x’i

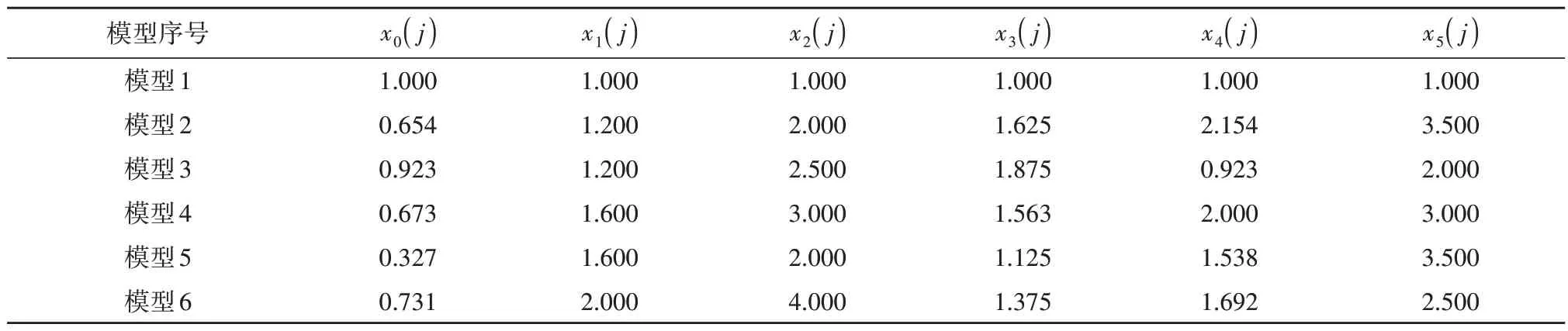
表13 无量纲化处理后母序列 x0和子序列 xiTable 13 Dimensionless processing of the parent sequence x0 and sub sequence xi

表14 关联度计算Table 14 Calculation of correlation degree

根据式（15）求得各个影响因子的关联度为［0.485、0.366、0.477、0.475、0.356］。根据计算结果，不同因子对路面塌陷沉降位移的影响灵敏度为：地下空洞跨径为x’1＞内摩擦角为x’3＞杨氏模量为x’4＞上覆土层厚度为x’2＞路面荷载为x’5。地下空洞跨径作为地下病害体规模因素，影响最大；内摩擦角和杨氏模量表征土体力学性质，作为岩土条件因素，影响次之；路面荷载影响最小，但是对地下空洞的扩张和塌陷的发生仍有不可或缺的作用。以上典型因素与地面塌陷风险评价体系指标权重计算结果一致，进而证明了层次分析法和熵权法组合赋权结果的合理性、有效性。

3 工程应用-以郑州市地面塌陷为例

3.1 工程概况

由地质雷达探测的建设路地下空洞位于河南省郑州市中原区，建设路与银行路交叉口附近。区内众多主干道路交叉纵横，车流量大，且地铁3号线与5号线在此交汇，地下结构复杂，由此推测其形成与地铁盾构施工有关。周围建筑不仅包括机电大厦家属院45号、46号居民楼，而且众多商业大厦坐落于此，人员密集程度较大，具体见图6交通平面位置图所示。

图6 交通平面位置图Fig.6 Traffic plan location map

由勘察资料及文献显示，建设路地下空洞风险区浅层空间地层岩性为砂土、黏性土双层结构（Zhao et al.，2020；张 建 羽 等，2023；Zhuo et al.，2023），遇强降雨时饱和松散砂土在地上地下交通动荷载作用下可能会丧失强度造成砂土液化现象，使地基失稳，空洞垮塌。该区地下空洞平面尺寸为1.0 m×2.8 m，其影响深度在地下0.41～0.73 m之间，净空0.32 m。周围分布有给排水管线、燃气管线、通信管线，隐患众多。

3.2 风险发生可能性评估

根据式（13）计算地下管线因素分值P1为：

同理，计算病害体因素分值P2和环境因素分值P3分别为87.07、66.48。

依据式（11），计算建设路地面塌陷发生的可能性P为：

通过有序加权法计算得郑州市建设路地面塌陷风险发生的可能性分值P为77.08，由表9城市地面塌陷风险发生可能性等级划分结果可知，该区风险等级为D级，近期发生可能性较大，应采取有效预防措施并定期巡查以及时掌握潜伏空洞变化情况（李斯等，2023）。另外，风险评价结果与地质雷达实测结果吻合度较高，可见评价模型具有一定的应用价值。

4 结论

本文以城市地面塌陷为研究对象，为避免塌陷发生造成的危害，以期建立一种合理且科学的风险评估方法，主要得到以下结论：

（1）在对郑州市近年来105处地面塌陷诱发因子进行了统计分析的基础上，综合了国内外专家对地面塌陷机理的分析，建立了以管线因素、病害体因素和环境因素为主的可能性风险评价体系。

（2）通过层次分析法和熵权法分别对风险体系各指标权重进行了计算并依据乘数归一法进行主客观组合赋权，结果显示病害体因素在城市地面塌陷中占据主导作用，其中地下病害体跨径占比为0.161、上覆土层厚度占比为0.113。

（3）为了验证主客观组合赋权的有效性，通过有限元软件数值模拟模拟与灰色关联度分析方法研究了五种典型因素对地下空洞塌陷引起路面沉降位移的影响程度。研究表明，影响因子灵敏度为：地下空洞跨径＞内摩擦角＞杨氏模量＞上覆土层厚度＞路面荷载，与可能性指标权重计算结果一致。

（4）依据有序加权法建立城市地面塌陷风险评估模型，并选取郑州市典型地下空洞案例进行风险评估分析，结果显示中原区建设路地面塌陷风险等级为D级，危害程度较高，应及时采取治理措施并定期巡查，预防灾害发生。

［注 释］

① 北京市勘察设计研究院有限公司.2018.城市地下病害体综合探测与风险评估技术标准： JGJ/T 437-2018［S］.

［附中文参考文献］

白凌燕，何静，王继明.2011.北京市地面塌陷特征与致灾因子分析［J］.地质灾害与环境保护，22（4）：41-45，49.

陈希，陈正.2023a.上海市中心城区道路地下空洞预判研究初探［J］.上海公路，（3）：1-5，216.

陈希，陈正.2023b.基于多属性决策法的宝山区东街村地下病害预判与分析［J］.交通与运输，36（S1）：266-270.

崔孝飞.2019.城市地下病害体风险评估技术研究［D］.郑州：华北水利水电大学：42-47.

葛伟亚，王睿，张庆，邢怀学，周洁.2021.城市地下空间资源综合利用评价工作构想［J］.地质通报， 40（10）：1601-1608.

侯超群，董满生，逄焕平.2013.松散土体型地面塌陷成因分析及机理研究［J］.合肥工业大学学报（自然科学版），36（1）：63-67.

蓝雄东.2023.城市地下管线渗漏诱发非饱和地层塌陷致灾机理研究［D］.济南：山东大学：3-13.

黎兵.2022.隐秘的灾害-地面塌陷［J］.中学科技，（18）：8-13.

李刚，李建平，孙晓蕾，赵萌.2017.主客观权重的组合方式及其合理性研究［J］.管理评论，29（12）：17-26，61.

李斯，杨自安，李冬月，张建国，鲁佳，尹佳.2023.基于无人机倾斜摄影三维建模技术的赤马山铜矿地质环境调查及评价［J］.地质与勘探，59（6）：1271-1281.

吕敦玉，余楚，侯宏冰，刘长礼，张云.2015.国外城市地质工作进展与趋势及其对我国的启示［J］.现代地质， 29（2）：466-473.

冉星星.2023.基于机器学习的深圳市地面坍塌灾害风险评估［D］.荆州：长江大学：36-61.

孙晓永.2020.基于综合层次分析法和熵权法的山区高速铁路选线研究［J］.交通节能与环保，16（03）：145-149，158.

王帅超.2017.城市地下管道渗漏引起的路面塌陷机理分析与研究［D］.郑州：郑州大学：28-47.

万志清，秦四清，李志刚，钱海涛.2003.土洞形成的机理及起始条件［J］.岩石力学与工程学报， 22（8）： 1377-1382.

仙永凯，史婧.2022.城市路面塌陷成因分析与隐患点管理方法［J］.中国高新科技，（3）：141-143.

许树柏.1988.实用决策方法—层次分析法原理［M］.天津：天津大学出版社：15-55.

许晓莹，陈斌.2021.城市道路空洞隐患风险评估方法应用研究［J］.市政技术，39（S1）：149-154，172.

杨木易.2023.基于AHP和改进熵权法的水资源配置与水循环分布合理度的综合评价［J］.水资源开发与管理，，9（9）：22-27，59.

叶远春，宋谷长.2012.城市道路空洞风险评估方法研究［J］.城市道桥与防洪，（4）：209-213，280.

易荣，贾开国.2020.我国城市地下空间安全问题探讨［J］.地质与勘探，56（5）：1072-1079.

曾灿军，陈卫忠.2018.城市地下空间开发强度预测模型研究［J］.地下空间与工程学报，14（5）：1154-1160.

张必昌，高国刚，刘瑞斌，刘亚明，段丹丹.2019.公路近区采空区地面塌陷风险性评价［J］.公路，64（12）：15-20.

张昌新，余志江，郑太航.2014.基于半定量法的地铁工程地面塌陷风险评估［J］.铁道工程学报，31（12）： 93-95.

张建羽，吕敦玉，刘长礼，王翠玲，孟舒然，刘松波，张云.2023.河南郑州市岩土地层结构特征及地下空间开发利用建议［J］.地质论评，69（1）：305-315.

赵延林，吴启红，王卫军，万文，赵伏军.2010.基于突变理论的采空区重叠顶板稳定性强度折减法及应用［J］.岩石力学与工程学报，29（7）：1424-1434.

钟世英，丛波日.2016.城市地面塌陷灾害成因机理分析及分类［A］.中国地质学会工程地质专业委员会.2016年全国工程地质学术年会论文集［C］.北京：工程地质学报杂志： 358-363.

周子勇，石浩宇，董毓良，凡伟伟.2023.基于层次熵权-云模型城市道路塌陷风险评价研究［J］.安全与环境学报，23（6）：1752-1761.