异步测量系统的分布式序贯椭球相交融合估计

周书玉, 张 鹏, 李孟委

(中北大学,a.仪器与电子学院; b.仪器科学与动态测试教育部重点实验室,太原 030000)

0 引言

单一传感器系统已经满足不了人们日益增长的需要。近年来,多传感器系统作为一个热门研究课题在传感器网络、导航定位定向、工业控制和人工智能等领域被广泛讨论[1-5]。多传感器系统可以提供更多的信息来对系统进行更精准的控制,使得多传感器系统的信息融合技术受到广泛关注,具有重要的研究意义[6]。在多传感器系统中,信息融合估计方法通常分为集中式融合估计和分布式融合估计,其原理是根据相应的融合算法将多个结果融合为一个更加可靠的结果[7]。集中式融合系统使用状态测量增强方法处理来自多个传感器的测量数据,这种方法虽然可以获得极佳的估计结果,但是,当某个传感器在工作中出现故障或损坏时,集中式系统不能及时检测和抛弃发生故障的传感器,会导致融合估计结果的可靠性下降、误差增加。相比之下,分布式融合系统具有独特的并行结构,并行结构的存在使得检测和隔离有故障的传感器变得容易,保证融合估计结果的正确性,所以分布式融合估计器具有良好的可靠性和灵活性[8-9]。为了提高多传感器系统的可靠性和灵活性,采用分布式融合系统是十分重要的。

在传感器网络中,测量数据受网络信道堵塞和拥挤等影响产生延迟是不可避免的,延迟现象的出现必定伴随着数据包丢失的情况,极大影响了系统的性能。对于存在网络信道堵塞和拥挤的系统,常采用将电流测量与测量延迟相结合的测量增强技术和复制重传的方法,将测量延迟的数据充分利用。但是,测量增强技术通过增广技术来解决融合估计问题,这必然造成计算复杂度的增加。文献[10]研究了具有马尔可夫链通信测量随机缺失系统的最优滤波问题,有效解决对测量缺失现象的描述问题。同时,文献[11]提出用一组伯努利分布的随机变量来描述随机测量缺失现象,也获得不错的效果。

在传感器测量采样工作中,当传感器测量采样频率与状态更新频率不同时,系统会出现传感器测量更新周期与状态更新周期异步化问题[12]。由于传感器采样频率总小于状态更新频率,常采用状态迭代的方法将具有异步采样的原始系统转化为在测量采样时刻同步采样的状态空间模型。但是,同步化的状态空间模型采样时刻只在传感器采样时刻进行,导致系统的状态更新点的信息缺失,严重影响滤波器对状态信息真实估计。为了对系统进行合理的滤波器设计,文献[13]提出一种切换Kalman滤波算法,这种算法不需要大量样本就可以保证滤波器的估计精度。

分布式融合技术可以保证系统的可靠性和灵活性。但是,当系统中各个传感器之间的相关性信息未知时,就无法将各个传感器提供的滤波结果进行融合[14]。目前,能够解决相关性未知的融合估计的方法主要有协方差相交(Covariance Intersection,CI)融合的方法和椭球相交(Ellipsoidal Intersection,EI)融合的方法。CI融合方法是通过对融合公式进行参数化而实现,它直接绕开了对传感器之间相关性信息的讨论,通过寻找一个可以表征传感器之间公共信息的最小化椭球进行描述。这种方法固然容易理解,但是缺少未知相关性的讨论必然会导致融合结果过于保守。为了追求精度更高的估计结果,在文献[15]中提出了EI融合的方法,重新定义一种参数化方法。它通过寻找可以表征相关性信息的最大化椭球,并将未知相关性信息用显性表达式描述出来,保证了融合估计结果的精度[16]。

1 多源异步测量系统结构设计

1.1 系统结构设计

本文针对具有网络信道堵塞诱导的测量缺失现象的多源异步测量系统状态估计问题,提出一种基于条件Kalman滤波算法的分布式序贯椭球相交(Distributed Sequential Ellipsoidal Intersection,DSEI)融合估计器来对系统进行融合估计。系统的结构如图1所示,主要分为同步化状态空间模块、局部滤波模块和融合估计模块。

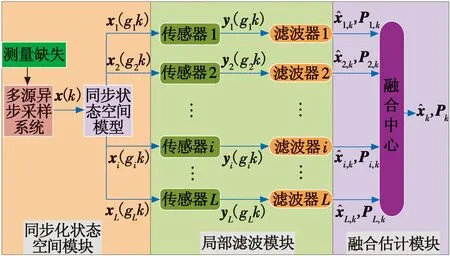
图1 多源异步测量系统的分布式融合估计结构Fig.1 Structure for distributed fusion estimation of multi-source asynchronous measurement systems

其中,同步化状态空间模块采用状态迭代方法将多源异步测量系统转换为在测量更新时刻同步采样的状态空间模型。同时,考虑到多传感器系统中网络信道堵塞或拥堵诱导的测量缺失现象的发生,本文通过一组随机的伯努利分布变量进行建模描述。

为了完整地对状态信息进行滤波估计,局部滤波模块通过条件Kalman滤波算法对系统进行滤波设计。在测量更新时刻输出滤波值,在状态更新时刻输出预测值。

融合估计模块选取融合估计精度更高的EI融合算法处理传感器之间未知相关性信息的融合估计问题,保证多源异步测量系统的融合过程的可靠性。

1.2 系统描述

首先,考虑一个多源异步测量系统,其状态空间模型为

x(k+1)=Ax(k)+Dω(k)

(1)

yi(gik)=Hix(gik)+vi(gik)i=1,2,…,L

(2)

其中:x(k)∈Rn,表示第k时刻的状态变量;yi(gik)∈Rmi,表示第i个传感器在采样时刻gik的测量值,gi∈N+,表示第i个传感器的采样周期;过程噪声ω(k)∈Rn和测量噪声vi(gik)∈Rmi分别服从均值为0、协方差矩阵Qω>0和Ri,k>0的不相关的随机白噪声;系数矩阵A,D和H分别是具有适当维数的常数矩阵。初始状态x(0)～N(μ0,P0),与ω(k)和vi(gik)不相关。

在多传感器系统中,由于网络信道的带宽有限,当多个测量信息进行传输时,会出现信道拥塞现象。信道拥堵现象会诱导测量延迟问题出现,即链路节点未能在更新时刻接收到测量数据,导致数据包丢失。由于测量缺失现象是随机发生的,所以本文通过一组随机伯努利分布变量来描述触发测量缺失的现象[7],即

yi(gik)=γi(gik)Hix(gik)+vi(gik)i=1,2,…,L

(3)

式中,γi(gik)是一个服从伯努利分布的随机过程,γi(gik)=1,表示第i个传感器在gik时刻成功对系统进行测量,反之,只能得到测量噪声。

在多源异步采样系统中,由于测量采样周期为状态更新周期正整数倍,需要将异步采样系统转换为在测量采样时刻同步采样的状态空间模型。以测量更新周期为gi的传感器为例,通过对式(1)进行gi次迭代,可以得到状态更新周期为gi的状态方程

x(gi(k+1))=Ax(gik+gi-1)+Dω(gik+gi-1)=
A2x(gik+gi-2)+ADω(gik+gi-2)+
Dω(gik+gi-1)=
Agix(gik)+Agi-1Dω(gik)+Agi-2Dω(gik+1)+
…+Dω(gik+gi-1)

(4)

将式(4)整理可得

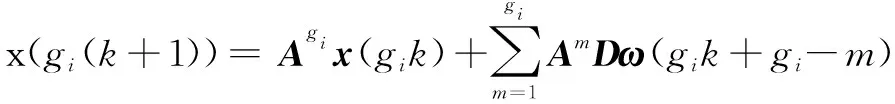
(5)

这样,具有测量缺失现象的多源异步采样系统式(1)～(3)就转化为多源同步采样系统,状态空间模型为

x(gi(k+1))=Agix(gik)+W(gik)

(6)

yi(gik)=γi(gik)Hix(gik)+vi(gik)i=1,2,…,L

(7)

转化后的同步系统只在测量更新周期的正整数倍的时刻进行采样,所以如何合理地设计一个滤波器来估计完整时刻的状态信息是十分重要的。

2 条件Kalman局部滤波

(8)

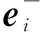
滤波估计结果表示为

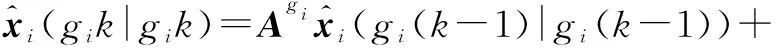
(9)

式中,εi(gik)为滤波过程的新息,即观测值减去预测观测值,

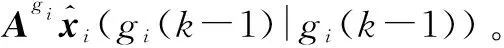
(10)

由于Kalman滤波增益的需要,新息εi(gik)的方差Qεi(gik)计算结果为

(11)

将其整理可得滤波器的增益矩阵Ki(gik)为

(12)

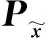
(13)

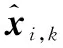
图2 条件Kalman局部滤波器流程图Fig.2 Flow chart of conditional Kalman local filter

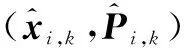
(14)

2) 情况2。当状态更新时刻与测量采样时刻不同步时,采用对上一时刻状态估计值的预测值来描述状态估计值,即

(15)

至此,就得到各个时刻的状态估计信息。在分布式系统中,为了获得精度更高的估计结果,如何选取一种合适的融合方法将各个传感器的滤波结果进行融合是至关重要的。

3 DSEI融合估计

在多传感器数据融合过程中,传感器之间的相关性信息不易获取,给融合过程带来了极大困扰。目前,处理未知相关性的融合问题时,常采用的融合方法是CI融合技术。CI融合技术通过寻找一个最小化椭球来界定未知相关性的范围,虽然这种方法被普遍接受,但CI融合技术侧重于分析融合公式,而不是对相关性进行描述,所以会导致融合结果过于保守[11]。为了获得精度更高的融合估计结果,EI融合技术通过引入新的估计量,将未知相关性信息用表达式进行明确的描述,通过寻找最大化的相关信息椭球范围精确地完成融合过程;并且EI融合技术将最优化问题通过代数表达式来描述,极大地降低了系统的计算复杂度。其既避免了保守估计,又兼顾了相关性信息的提取,融合后的精度也得到保证。

在多传感器数据融合过程中,基于双传感器的融合估计的一般式为

(16)

式中,Kfus和Lfus表示融合增益,相应的协方差矩阵为

(17)

式中,PAB=PBA,表示交叉协方差矩阵。融合增益是通过求解最小化的协方差矩阵Pfus的迹来确定的,所以解决融合问题的关键在于获得传感器之间交叉协方差矩阵的信息。

为了对传感器之间的相关信息进行明确描述,将式(16)改写为

(18)

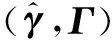
(19)

融合估计的目标就是要获得传感器之间的公共信息[15]。在EI融合算法中,利用传感器提供的信息将描述公共信息相关特征用代数表达式描述为

(20)

(21)

其中:S表示特征向量矩阵;Τ表示特征对角矩阵;η控制融合结果的精度。相关性信息的特征对角矩阵表示为

ΤΓ=max{ΤA,ΤB}。

(22)

分别将式(20),(21),(22)代入式(18),(19)获得EI融合估计结果。

基于上述分析,EI融合技术将传感器之间的未知相关性信息利用代数表达式来表示,降低融合过程的计算成本。因此,对于多传感器系统的融合估计,本文通过在分布式融合结构下,将多个传感器的滤波值按照序贯融合方法两两融合,进行L-1次的EI融合过程,得到最终的融合估计[11]。设计的DSEI融合估计器为

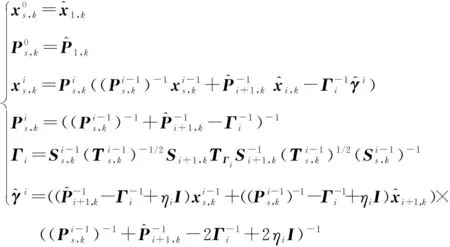
(23)

为了直观地描述EI融合技术的优越性,通过一个简单的数值实例对CI融合、EI融合技术进行分析。首先假设有两个滤波估计器XA,XB,然后分别采用CI融合技术和EI融合技术进行融合估计。其中,滤波估计器XA滤波值为xA=[0.5,1]T,误差协方差矩阵为PA=[2.5,-1;-1,1.2],滤波估计器XB滤波值为xB=[2,1]T,误差协方差矩阵为PB=[0.8,-0.5;-0.5,4]。两个滤波估计器的融合结果如图3所示。结果表明,CI融合算法所围的区域大于EI融合估计所围的区域,与两个滤波估计器的公共信息相比,CI融合估计结果过于保守,而EI融合估计保证了融合结果的精准性。

图3 CI融合算法与EI融合算法的比较Fig.3 Comparison between CI fusion algorithm and EI fusion algorithm

对于所设计的分布式序贯椭球相交融合估计器,通过分析估计器的一致性问题来证明融合估计优于各个传感器提供的滤波器的估计结果。

首先,选择传感器1和2的滤波结果进行融合,由式(22)和矩阵的迹的相关理论可知,公共信息Γ是包含滤波值x1和x2的最大化椭球,即

(24)

(25)

(26)

根据数学归纳法,在分布式序贯椭球相交融合估计器中经历L-1次的EI融合过程,最终的融合误差协方差矩阵小于每个滤波器提供的误差协方差矩阵

(27)

通过上述分析,本文所设计的分布式序贯椭球相交融合估计器具有良好的一致性,且融合估计器的性能优于各个滤波估计器。

4 仿真研究

为了直观地验证所提出的基于条件Kalman滤波的DSEI融合估计算法的有效性,本文通过构造一个稳定时变的线性数值实例来验证DSEI融合估计器的优越性能,既保证系统状态值的有界性,又保证系统估计结果的可靠性。具有测量缺失的多源异步测量系统为

(28)

式中:状态变量x(k)=[x1(k),x2(k),x3(k)]T;状态系数矩阵A=diag(a1,a2,a3),矩阵中各元素的表达式为

(29)

各传感器的测量矩阵分别为

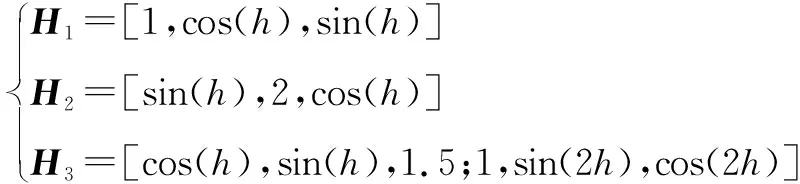
(30)

系统参数h=0.2。系统中各传感器出现的测量缺失现象通过服从伯努利分布的随机变量γ进行描述,变量参数分别为γ1=0.9,γ2=0.7,γ3=0.4。过程噪声的系数矩阵D=diag(1,1,1),协方差矩阵Q=diag(1,1,1),测量噪声分别为R1=0.2,R2=0.3,R3=[0.3,0.1;0.1,0.25]。初始状态值和协方差矩阵设为:x0=[0.1,0.1,0.1]T,P0=diag(0.1,0.1,0.1)。

为了准确地评估所提出DSEI融合估计算法性能,通过分析估计结果的均方根误差(RMSE)来验证算法的可靠性,即

(31)

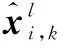
通过对所提出的基于条件Kalman滤波的DSEI融合估计算法与现有分布式序贯协方差相交(Distributed Sequential Covariance Intersection,DSCI)融合估计算法进行对比仿真实验,得到对状态信息的估计结果。两种算法的状态跟踪性能结果如图4所示,可以看出DSEI相比于DSCI的融合估计结果,更能对状态变量实现良好的跟踪性能。

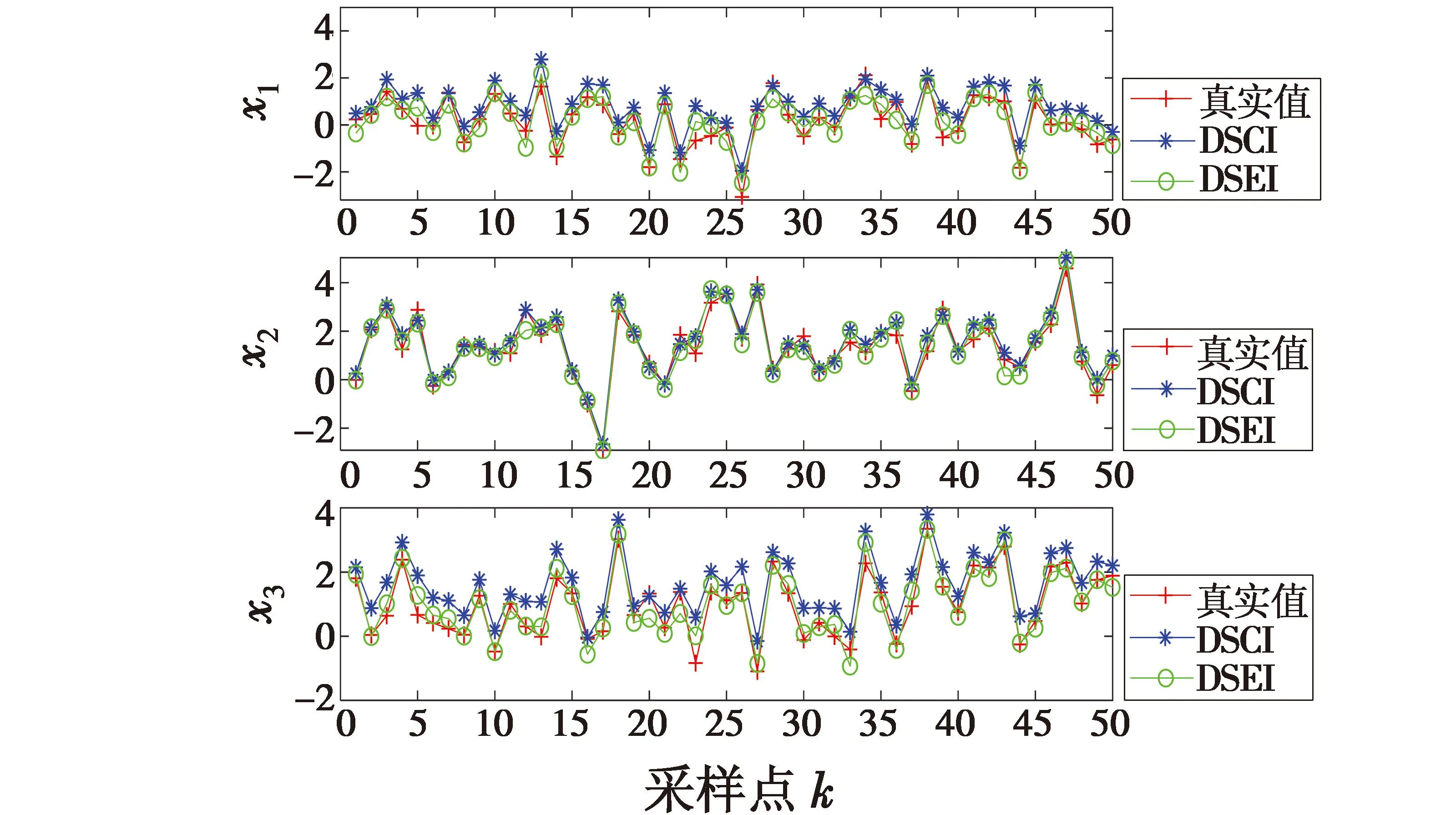
图4 DSCI和DSEI融合估计算法的状态跟踪性能Fig.4 State tracking performance of DSCI and DSEI fusion estimation algorithms

同时,为了进一步验证DSEI融合估计器的性能,本文对局部滤波估计器、DSCI和DSEI融合估计器的估计结果的RMSE进行分析,其对比结果如图5所示。结果表明,DSEI融合估计结果的各个状态RMSE均小于局部滤波估计,同时,DSEI融合估计结果的RMSE也小于DSCI融合结果,保证了融合结果的准确性。

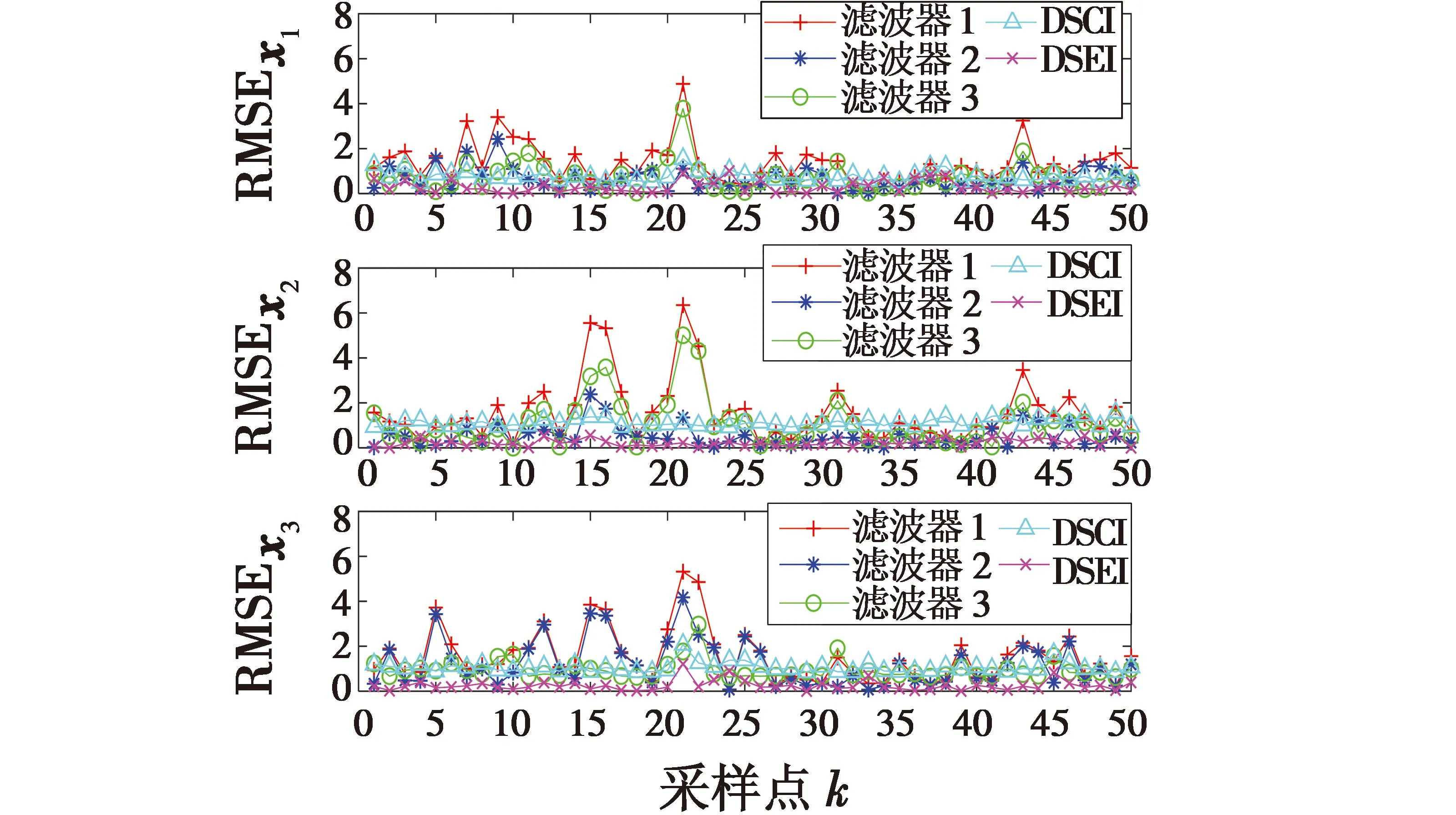
图5 局部滤波与DSCI,DSEI融合估计结果的RMSE对比Fig.5 Comparison of RMSE of local filtering with DSCI and DSEI fusion estimation results

进一步,为了验证DSEI融合算法相较DSCI融合算法在分布式融合系统中发挥的良好估计性能,本文比较了DSCI和DSEI融合估计的误差协方差矩阵的迹,即矩阵的迹越小,误差范围越小。两种算法的误差协方差矩阵的迹的对比如图6(a)所示。结果表明,DSCI融合结果的误差协方差矩阵的迹大于DSEI融合,且DSEI的误差范围缩小为DSCI的35%,大大提高了系统融合结果的可靠性。

图6 DSCI和DSEI融合估计对比Fig.6 Comparison of DSCI and DSEI fusion estimation

同时,本文还对DSCI和DSEI融合估计算法在运行过程中的计算时间成本进行对比,结果如图6(b)所示。结果表明,DSEI融合估计算法的迭代运行时间要短于DSCI融合估计算法。其中,DSEI融合估计算法迭代运行时间约0.002 885 s,可以控制在3 ms范围内,而DSCI的迭代运行时间约0.030 756 s。DSEI融合算法计算成本低的原因是将融合过程最优化问题进行显性描述,显性表达式会大大降低运行过程的计算成本,从而加速融合结果的输出。

5 结束语

本文针对网络信道堵塞诱发测量延迟现象的多源异步测量系统的状态估计问题,提出了一种基于条件Kalman滤波的DSEI融合估计算法。该算法主要分为同步化状态空间模块、局部滤波模块和融合估计模块。在同步化状态空间模块中,系统对测量缺失现象采用一组服从伯努利分布的随机变量描述,并利用状态迭代方法将多源异步测量系统在测量更新时刻同步化;局部滤波模块采用条件Kalman滤波算法对系统噪声进行滤波处理,在状态更新与测量更新时刻同步时输出滤波值,否则输出状态预测值,完整地对状态信息进行滤波估计;融合估计模块在不考虑传感器之间相关性信息的前提下,采用了DSEI融合估计算法将局部滤波器提供的滤波结果进行融合。最后通过一个数值仿真实验验证了所提算法的优越性能,DSEI融合估计误差精度相较DSCI提高了35%,迭代运行时间也可以控制在3 ms内,保证了融合结果的可靠性能。