空间机器人预定义任意时间最优轨迹规划
刘宜成, 张飞越, 严 文
(四川大学电气工程学院,成都 610000)
0 引言
太空探索是人类的一项重要活动,而太空卫星通常被视为其中不可或缺的一部分[1-2],然而,每年都有许多卫星因部件老化或微陨石撞击而报废,这些卫星很可能对其他正常卫星形成二次撞击[3]。因此,为了减少不必要的损失,卫星回收成为空间机器人的重要任务,同时也需要运用机器人避障算法,使其能够安全完成任务,不成为下一个碎片[4]。
双臂六自由度机器人因其灵活性和通用性,常被安装在卫星基座上执行捕获任务,空间机器人也自由浮动完成捕获任务。因此,机械臂和卫星基座之间的动态耦合可能会导致基座的姿态偏差,从而增加末端执行器的跟踪误差[5]。为了保持基座姿态稳定,一些研究者在轨迹规划算法中采用了平衡臂的运动规划策略来抵消动力学耦合。文献[6]提出了一种基于迭代搜索的双臂运动规划方法来稳定基座的位置,但没有考虑姿态;文献[7]提出了一种同时减小基座位置和姿态误差的零内力协调动力学控制方案;文献[8]提出了一种带有姿态反馈的轨迹规划策略,以消除奇异避免和自碰撞避免方法带来的误差,但它不能很好地处理较大的累积误差,并且收敛时间也无法预测。
基于反馈的轨迹规划的本质是将机械臂的关节角速度作为控制输入,将基于位姿误差的运动学方程得到的速度级位姿误差作为系统输出,如果引入指数反馈代替比例反馈,关节角速度的增加将不可避免。文献[9]将遗传算法应用于轨迹规划,以获得平滑的关节角速度轨迹,但没有主要考虑跟踪误差;文献[10]利用改进粒子群算法实现轨迹寻优。但上述方法都不能从理论上解决误差消除的问题,如果存在奇异点、障碍物等外界干扰,误差必然会增大。
针对上述问题,本文研究了基于新型优化算法的双臂自由漂浮空间机器人(FFSR)预定义任意时间快速避碰轨迹规划,并采用布谷鸟搜索算法进行参数优化以获得更加平滑的运动轨迹的问题。本文主要目的是研究如何获得空间机器人的最优轨迹规划方案,空间机器人模型将采用之前研究中成熟的基于姿态误差的运动学模型[11]。
1 理论基础
考虑一个系统
(1)
式中:x∈Rn,是系统的状态变量;ϑ∈Rn,是系统的参数;f:R+∪{0}×Rn→Rn,是一个非自治的非线性函数;原点x=0是式(1)的一个平衡点,初始时间t0∈R+∪{0}。
定义1固定时间稳定。
如果系统式(1)是全局有限时间稳定的(即它是全局渐近稳定的且式(1)的任何解:x(t,t0,x0)=0,∀t≥t0+T(t0,x0) ,T≥0,是稳定时间),并且时间函数T(t0,x0)是有界的(即∃Tmax>0∶T∀x0∈Rn且∀t0≥0,T(t0,x0)≤Tmax),那么系统式(1)的原点是固定时间稳定的。
定义2预定义任意时间稳定[12]。
当满足以下条件,系统式(1)的原点是预定义任意时间稳定的。
1) 系统是固定时间稳定。
2) ∃Ta>0,这与系统参数ϑ无关,而且可以预先定义。
3)对于任何给定的ϑ,下列任一项都可以成立:
①Ta>Tes,为弱任意时间稳定;
②Ta=Tes,为强任意时间稳定。
其中,Ta是系统式(1)的轨迹收敛到原点的稳定时间;Tes是系统式(1)的轨迹收敛到原点的精确稳定时间(实际时间)。
引理1[12]考虑系统式(1),假设它的平衡点x=0包含在集合D⊂Rn中。假设D上存在两个连续正定函数β1和β2。还需假设存在一个实值连续可微函数V∶[t0,∞)×D→R+∪{0}。假设存在一个实常数η>1使得下列条件成立:
1)β1(x)≤V(t,x)≤β2(x)∶∀t>t0,∀x∈D{0},
2)V(t,0)=0∶∀t≥t0,
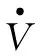
上述理论基础突出了预定义任意时间稳定系统的李雅普诺夫候选函数的关键特征。
2 基于姿态误差的运动学建模
双臂FFSR系统模型如图1所示。
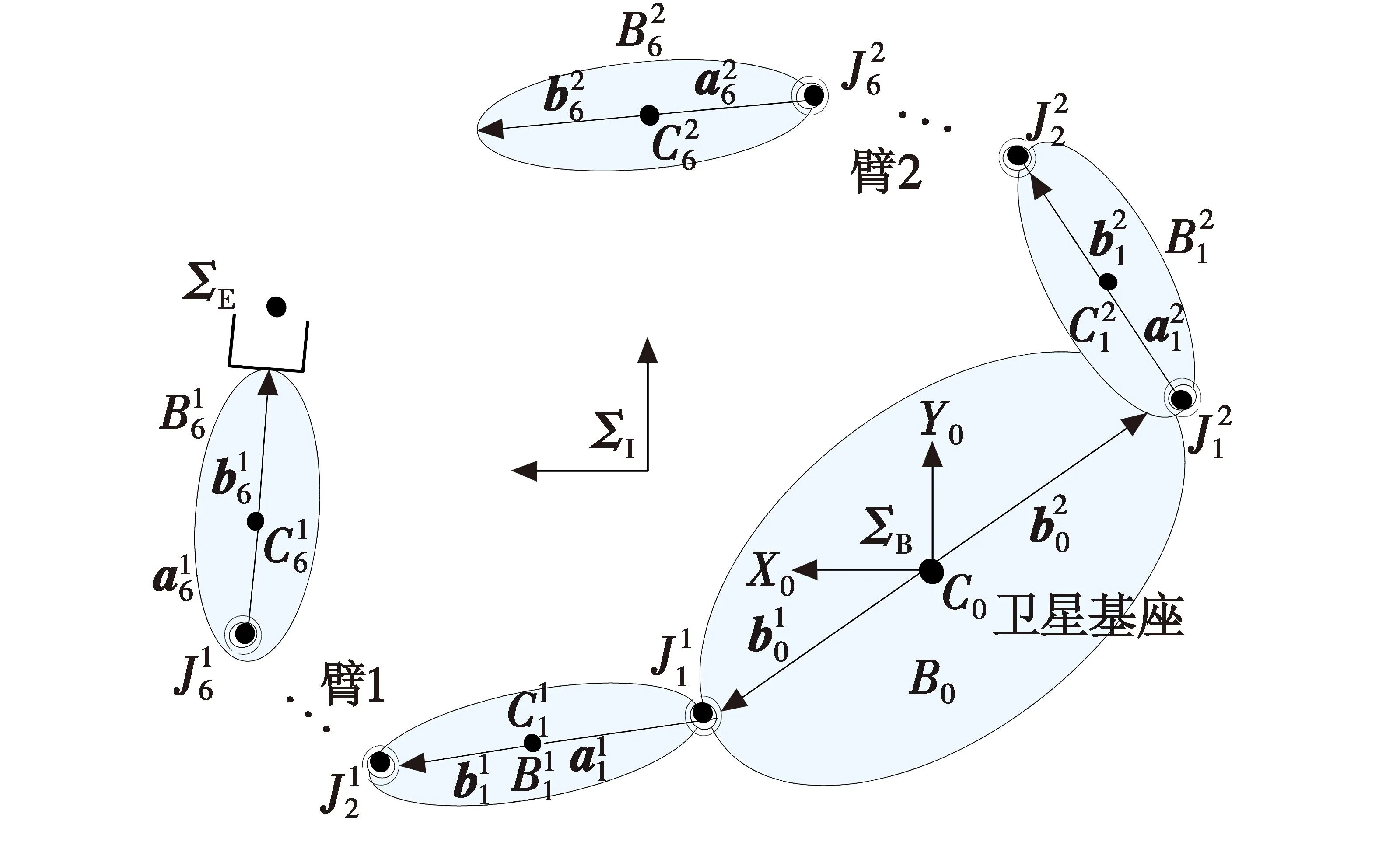
图1 双臂FFSR系统模型Fig.1 Model of a dual-arm FFSR system
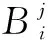
根据文献[11]中的位姿误差运动学方程,末端执行器和基座的位姿误差运动学关系可以表示为
(2)
(3)
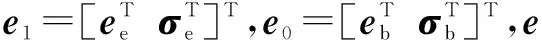
(4)
E3是一个三阶单位矩阵;Red∈R3×3,Rbd∈R3×3,是将参考坐标系转换为固定在末端执行器或基座上的坐标系的旋转矩阵;姿态误差G(σ)根据修正的罗德里格斯参数(MRP)[13]得来,即
3 轨迹规划
3.1 双臂FFSR的非奇异轨迹规划
(5)
(6)
式中:常数η>0;tp为规划开始时间。
然后,根据式(2),(3),(5)和(6),可以推导出一个新型的具有预定任意时间收敛的FFSR的联合角速度轨迹
(7)
(8)

(9)

(10)

(11)
式中:λm为阻尼因子;εj为奇异阈值。
3.2 双臂FFSR的避障轨迹规划
在太空中,漂浮的卫星碎片和行星碎块可能会对机械臂造成碰撞风险。因此,采用文献[8]中基于CDF的轨迹规划方法来使空间机器人避免碰撞,式(9)和式(10)可以修正为
(12)
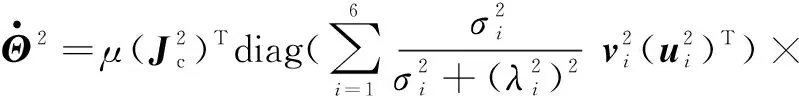
(13)

(14)
式中:Lp=max‖CDF(p)‖,CDF是机械臂和障碍物之间碰撞场的风险函数;常数ξ<1;Δ为碰撞的阈值。
4 基于布谷鸟搜索算法的双臂FFSR最优轨迹规划
即使在空间机器人的轨迹规划中采用避奇异策略,仍然存在一个制约捕获任务成功的大问题,即机器人关节角速度的过饱和。机械系统的最大关节角速度不得不控制在有限的范围内,如果机械臂长时间停留在较大的关节角速度下,其耐久性将受到严重影响,在此情况下,甚至齿轮也可能扭曲断裂。因此,在FFSR系统中应该对关节角速度进行优化,以获得更小、更平滑的机械臂关节角速度。本文在轨迹规划过程中采用了基于布谷鸟搜索算法的优化策略,对参数η,tf,tp进行优化,以获取符合上述要求的更小、更平滑的关节角速度曲线。目标函数B为

(15)

(16)
关节角速度Θb的限制因子为
(17)
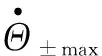
布谷鸟搜索算法的灵感来源于自然界中布谷鸟利用随机或类似随机的飞行来寻找适合自己产卵的巢的行为。为了模拟布谷鸟的繁殖策略,对布谷鸟搜索算法假设了以下3种理想状态[14]。
假设1 每只布谷鸟一次只下一枚蛋,随机选择一个巢进行孵化。
假设2 在一组随机选择的巢中,优质的巢会保留到下一代。
假设3 可用巢的数量是固定的,巢主发现外来鸟蛋的概率是Pa∈[0,1]。当巢主发现一枚外来的鸟蛋时,它会丢弃这个布谷鸟蛋或者重建一个新的巢。
基于上述3种理想状态,布谷鸟寻找其宿主巢的位置和路径的更新算式为
(18)
式中:

(19)
根据以上过程,布谷鸟搜索算法的实现过程[15]如下。
1) 初始化:设置种群大小、搜索空间维数、最大迭代次数等参数。随机初始化鸟巢的位置Xi,i∈[1,n],定义目标函数B(X),X=[X1,X2,…,Xn]T。
2) 计算并比较每个鸟巢位置的目标函数值,得到当前最优函数值。
3) 使用式(18)更新除最优巢之外的其他巢的位置和状态,计算目标函数值,并将获得的函数值与当前最优函数值进行比较。如果更好,则更新并记录当前的最佳值。
4) 位置更新后,随机数r与Pa比较。如果r>Pa,则随机更新鸟巢位置,否则,嵌套位置保持不变。
5) 如果满足最大迭代次数或搜索精度要求,则继续下一步,否则返回3)。
6) 输出全局最优鸟巢位置。
5 基于布谷鸟搜索算法的双臂FFSR最优轨迹规划
本文使用的空间机械臂模型是PUMA560型,其D-H结构[16]如图2所示。
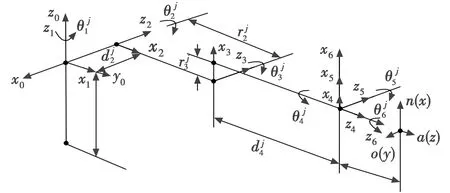
图2 臂j的D-H框架Fig.2 The D-H frame of Arm-j
D-H和机械臂的参数如表1和表2所示。仿真步长为ode45,FFSR系统的初始动量均设为零,仿真时间为20 s。

表1 PUMA560型机械臂j的D-H参数Table 1 The D-H parameters of PUMA560-type robotic Arm-j
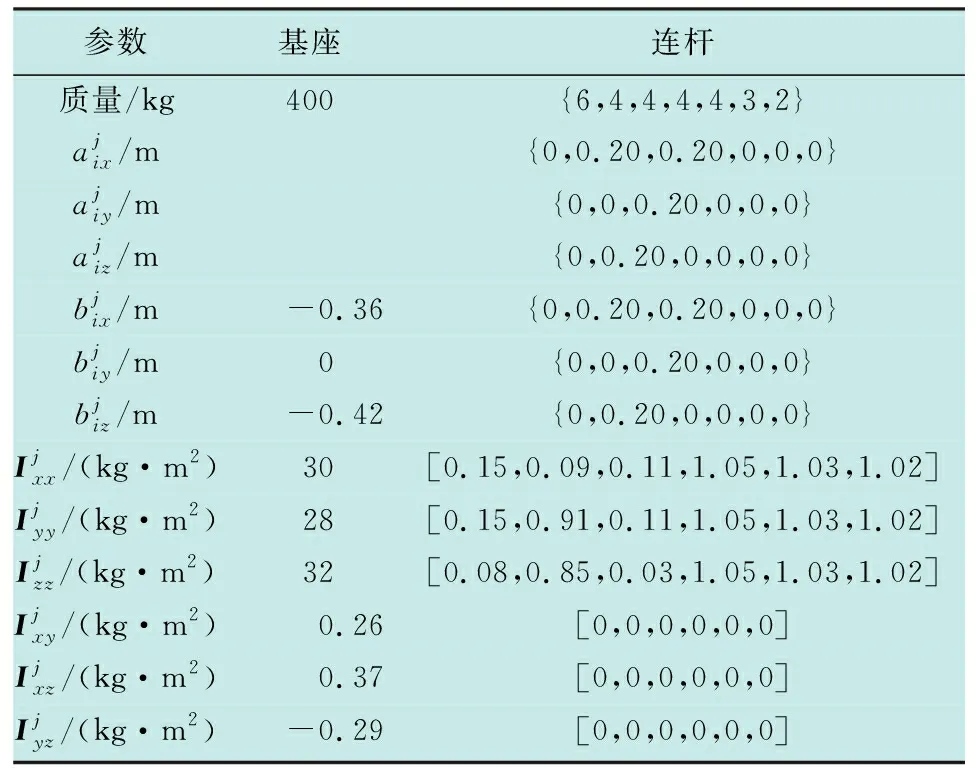
表2 臂j的数学特性Table 2 The math properties of Arm-j
基座的初始姿态和初始位置分别为:σb0=[1,0,0,0]T;pb0=[-0.2832,0.3107,0.3248]T,单位为m。
末端执行器的初始位姿和初始位置分别为:σe0=[0,0.8191,0,0.5736]T;pe0=[-0.2832,0.3107,0.3248]T,单位为m。
目标的位置和姿态分别为:pt=[0.7147,0.4150,-0.1758]T,单位为m;σt=[0.0215,0.9027,0.1184,0.4132]T。
障碍点的位置:po=[-0.0691,0.6037,0.4742]T,单位为m。
危险半径被设置为0.3 m。
DLS算法的初始参数设置为:λm=0.08,εj=0.02。
末端执行器的期望梯形速度级轨迹如图3所示,采用文献[16]中的速度级路径规划方法来获得末端执行器的期望梯形速度轨迹。
5.1 基于姿态反馈的双臂FFSR预定义任意时间收敛轨迹规划
为了比较本文算法与之前算法的跟踪精度,对基于CDF的具有基于比例收敛的姿态反馈的轨迹规划方法[8](对比方法1)、无姿态反馈避障算法[17](对比方法2)和无避障的轨迹规划方法[11](对比方法3)进行仿真,以便与本文方法进行比较。基于CDF的避障算法的参数设置为ξ=0.1,Δ=17.25。
障碍点和手臂之间最近距离的曲线如图4所示,可以看出本文方法和其他基于CDF的轨迹规划方法可以防止机械臂撞到障碍点,而没有避障算法的轨迹规划方法会使机械臂最近距离到达0.233 9 m,使其撞到障碍物。

图4 障碍点和手臂之间最近距离的曲线Fig.4 Curve of the closest distance between the obstacle point and the arm
末端执行器的误差曲线如图5所示。

图5 末端执行器的误差曲线Fig.5 Error curves of the end-actuator
由图5可以看出,本文方法和基于比例反馈的方法可以使误差收敛到零的小邻域,但是在没有避障的轨迹规划方法中,末端执行器的位置误差无法消除。将基于比例姿态反馈的方法与本文方法进行比较,很明显,通过比例反馈难以消除由避障引起的累积误差,但是本文算法做得更好。
为了比较本文所提预定义新型轨迹规划算法与之前算法的收敛速度,将对比传统的预定义时间轨迹规划算法[18](对比方法4)。对比在20 s内的收敛速度,将两者的时间参数都设置为20 s。预定义时间比较末端误差曲线如图6所示,本文方法收敛速度更快。

图6 预定义时间比较末端误差曲线Fig.6 Comparison of end error curves in predefined time
5.2 基于布谷鸟搜索算法的参数优化
在上述预定义任意时间轨迹规划方法的基础上,研究了一种基于布谷鸟搜索算法的参数优化策略。类似于所有的有限时间反馈控制,指数项部分会导致初始控制输入,也就是机械臂的角速度变得非常大[19]。因此,为了提高机械手的耐用性,需要优化参数以获得最佳的关节角速度轨迹。
比较方法是提出的基于布谷鸟搜索算法的优化算法和无优化算法的预定义任意时间轨迹规划,公平起见,比较方法的预定义时间函数形式和时间参数是一致的。布谷鸟搜索算法的每一代最优适应值如图7所示。
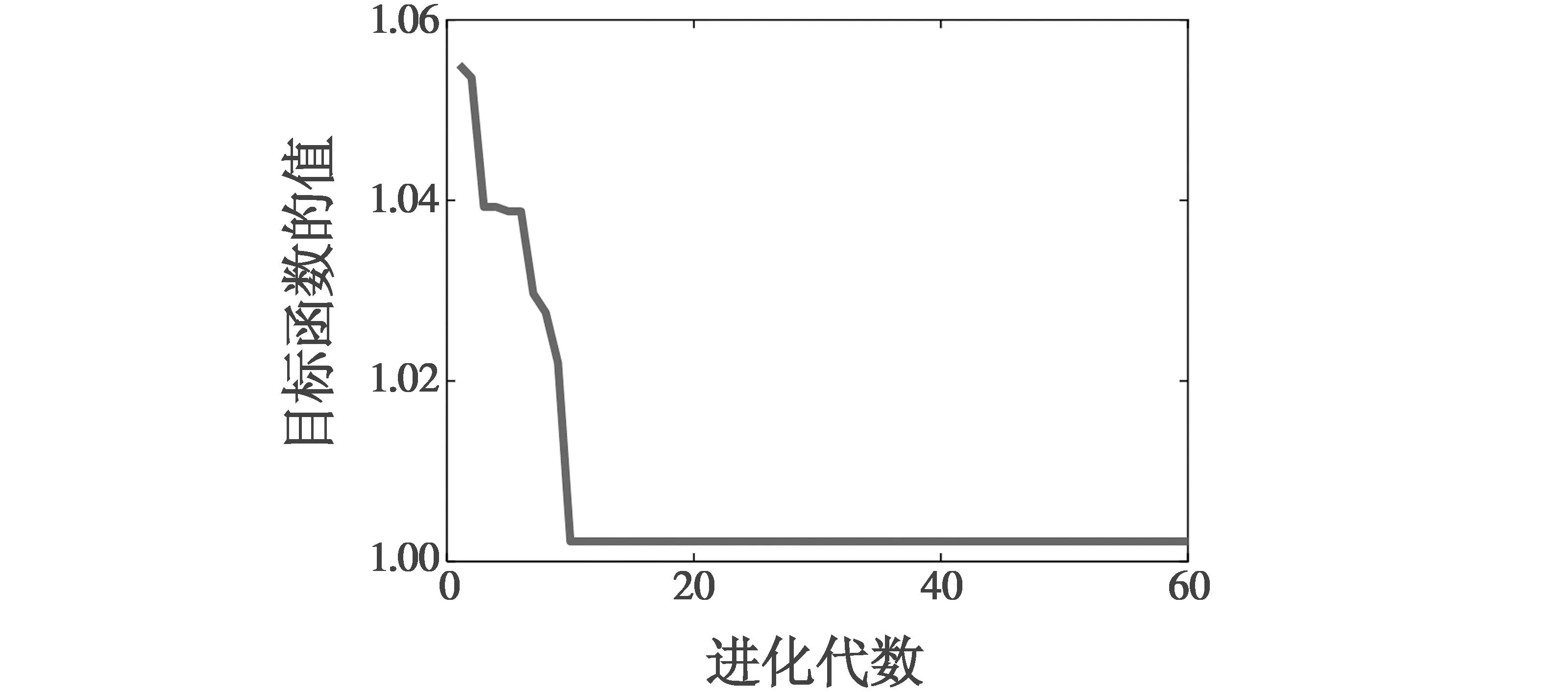
图7 布谷鸟搜索算法的每一代最优适应值Fig.7 Each generation optimal fitness value of CS algorithm
根据图7中的结果,最佳预定义任意时间参数可以被设置为η=1.0082,tf=19.9212 s,tp=0.7224 s。没有布谷鸟搜索算法优化的预定义任意时间参数可设置为η=15.0,tf=19.9212 s,tp=0.7224 s。
关节角速度如图8所示。


图8 关节角速度Fig.8 The joint angular velocity
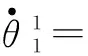
基于布谷鸟搜索算法的末端执行器位置误差曲线如图9所示。根据图9,末端执行器的位姿跟踪精度也能得到保证。末端执行器的最终误差限制在10-6量级内。

图9 基于布谷鸟搜索算法的末端执行器位置误差曲线Fig.9 Position error curve of the end-actuator in the proposed method with CS algorithm
6 结束语
本文设计了一种FFSR系统的可实现误差预定义时间收敛的新型轨迹规划算法,通过把传统预定义时间用任意时间替换,实现了更快的反馈误差收敛。如果在基于位姿的运动学方程中应用反馈来获得误差快速响应形式,平衡臂的关节角速度将变得过大,可能超过最大关节角速度的工作空间,产生损坏机构驱动系统的后果,因此,本文在空间机器人的轨迹规划中采用基于布谷鸟搜索算法的优化策略,以获得小而平滑的关节角速度轨迹。但是,不同于传统的机械手轨迹规划优化策略,本文不再同时考虑跟踪误差和轨迹的平滑性,而是应用预定义任意时间的姿态反馈来获得理论上的零误差跟踪精度,从而可以在使用布谷鸟搜索算法时只考虑轨迹的平滑性。最后仿真表明,本文提出的轨迹规划策略能够在预定义的时间内实现末端执行器更快速的误差收敛,而且使用布谷鸟搜索算法优化参数后能够得到更平滑的轨迹。

