船用双层壳体齿轮箱柔性动力学建模及隔振性能分析研究

杨 杰，朱如鹏，陈蔚芳，戴光昊,岳彦炯,尹逊民

（1.常州工学院航空与机械工程学院/飞行学院，江苏 常州 213032；2.南京航空航天大学机电学院，南京 210016；3.中国船舶集团有限公司第七〇三研究所，哈尔滨 150078）

0 引 言

舰船齿轮箱的过度振动不仅会降低其使用寿命，而且会引起机舱水下辐射振动噪声的增大，影响舰船的隐蔽性，因此对舰船齿轮箱振动噪声控制尤其重要[1]。现今，主要利用优化壳体肋板分布[2]、在壳体表面敷设阻尼材料[3]、在轴承上安装阻尼支撑圈[4]等手段来控制齿轮箱体辐射噪声。此外，还通过在齿轮箱与舱体之间安装弹性支撑[5]、多层径向隔振元件[6]、周期性复合材料支撑柱[7]等措施来减少齿轮箱振动向舱体的传递。这些减振降噪的措施在一定程度上改善了齿轮箱的振动噪声。为了进一步控制齿轮传动系统振动向齿轮箱安装基座的传递，王梦琪等[8]提出了一种从齿轮箱内部隔离齿轮传动系统振动的隔振技术，该技术通过在双层壳体齿轮箱的内外层壳体之间布置隔振器来实现振动噪声控制，其隔振效果可达到12 dB，且通过研究表明优化隔振器参数可提高双层壳体齿轮箱隔振性能[9-10]。对于双层壳体齿轮箱这种大功率、重负载、高冲击、高频下的动力传动装置，有三个重要核心部件：内层壳体、外层壳体和隔振器。特别是，齿轮箱内外壳体存在薄壁结构，在隔振器参数设计不当时可能存在共振与模态耦合振动现象。因此有必要对双层壳体齿轮箱进行柔性高效高精度的动力学建模与振动特性分析。

目前主要有两种方法对双层壳体齿轮箱进行柔性动力学建模：一种为采用有限元方法对齿轮箱完全建模；另一种为使用模态综合法对齿轮箱整体缩聚建模。然而，前者建立的完全有限元模型使得系统的自由度巨大且在与传动系统动力学模型耦合求解时效率低[11]，后者建立的缩聚模型精度难以把握且对隔振器参数优化繁琐[12-13]。因此，本文将双层壳体齿轮箱的内外壳体分别设置为独立子结构，采用模态综合法对各子结构有限元模型进行缩聚；再以齿轮箱内外壳体的隔振器结合处为连接点，通过隔振器的刚度和阻尼矩阵实现两个子结构缩聚模型组装，进而形成整体的双层壳体齿轮箱的缩聚模型。该缩聚模型考虑了不相邻的离散质量块在空间上多向耦合问题[14-15]，而且还可以实现齿轮箱整体结构模型在工程关注的固有频率内近似等效。

由于双层壳体齿轮箱的内壳体采用隔振器支撑，导致内壳体支撑刚度降低，易诱发内壳体刚体振动。若齿轮箱的内壳体刚体振动与外壳体弹性振动产生耦合，可能会出现共振现象[16]，使得齿轮箱产生更为严重的振动噪声。因此，本文通过广义弹性力能量解耦法[17]探讨双层壳体齿轮箱的模态振动耦合机理，再分别从模态解耦率、模态贡献度、振级落差和倾斜度四个方面对双层壳体齿轮箱的隔振性能进行综合评估，为船舶齿轮箱隔振降噪的设计提供理论基础。

1 双层壳体齿轮箱的柔性动力学建模

双层壳体齿轮箱是由外壳体、内壳体和隔振器等组成，如图1所示。在齿轮箱的内壳和外壳之间按辐射式安装隔振器，以实现齿轮传动系统与齿轮箱隔离，达到降低振动噪声目的。隔振器中的橡胶材料属于超粘性和高弹性材料，为了简化计算，本文将隔振器简化为具有刚度和阻尼性能的弹簧单元。

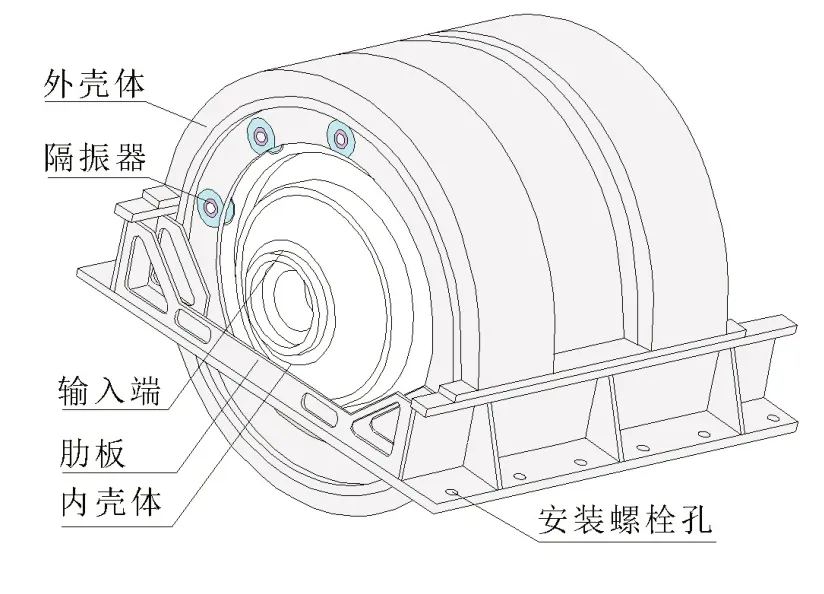
图1 双层壳体齿轮箱结构示意图Fig.1 Schematic diagram of a double-layer gearbox casing

针对双层壳体齿轮箱结构复杂且尺寸大的特点，通过模态综合法对齿轮箱原有限元模型的自由度进行降维和变换可以实现模型的缩聚，从而降低了原模型的自由度[18]。基于模态综合法建立双层壳体齿轮箱的柔性动力学模型的流程如图2 所示。首先，将双层壳体齿轮箱的内外层壳体分别设置为单独子结构模型；其次，在各子结构的结合点和结构特征点处建立缩聚点；再次，根据内外层壳体之间的实际位置关系，将缩聚子结构模型的刚度矩阵和阻尼矩阵组装成整个齿轮箱的缩聚模型；最后，由于双层壳体齿轮箱的柔性动力学建模的精度与各子结构缩聚模型中缩聚点的位置和数量有关[19]，通过齿轮箱的缩聚模型与原始模型的固有特性对比分析，调整缩聚点的位置和数量，以满足该缩聚模型的有效性。

图2 柔性双层壳体齿轮箱动力学建模流程图Fig.2 Flexible modeling flow chart of a double-layer gearbox casing

图3给出双层壳体齿轮箱缩聚点位置示意图和缩聚模型。在内外层壳体的输入端和输出端的隔振器底座处设置缩聚点，用于内外壳体子结构模型的连接。此外，在每个子结构的结构特征处（如轴承座、机脚、中心点等）设置缩聚点，这些缩聚点与齿轮箱的结构特征处主节点刚性耦合。

图3 双层壳体齿轮箱模型Fig.3 Model of a double-layer gearbox casing

通过模态综合法获得双层壳体齿轮箱的各子结构缩聚质量矩阵Mτg和刚度矩阵Kτg。假设内外壳体中有Nτ个缩聚点，缩聚的Mτg和刚度矩阵Kτg可写成为

式中，a和b分别代表双层壳体齿轮箱内外壳体，交叉子矩阵Mτij和Kτij（i≠j;i=1,2,…,Nτ;j=1,2,…,Nτ）为输出齿轮箱外壳体子结构各缩聚点的耦合质量矩阵和阻尼矩阵，主子矩阵Mτii和Kτij为外壳体子结构缩聚点的主质量矩阵和阻尼矩阵。子矩阵Mτij和Kτij均为6×6的方矩阵，即对应缩聚点的3个平动自由度和3个转动自由度。

将各个子结构缩聚矩阵按连接关系进行组装，从而建立双层壳体齿轮箱的缩聚模型。实际上，齿轮箱安装螺栓的连接属于典型的刚性连接子结构，与其它缩聚点没有偶联作用。内壳体和外壳体通过隔振器来解决双层壳体齿轮箱模型连接问题，隔振器的刚度和阻尼如表1。根据隔振器在双层齿轮箱的位置，将输入端和输出端的各隔振器刚度矩阵和阻尼矩阵通过变换转移到各子结构缩聚模型的隔振器缩聚点位置，进而确定内层壳体和外层壳体的隔振器刚度Kioa和Kiob及对应的阻尼矩阵Cioa和Ciob，以及内层壳体与外层壳体之间的耦合矩阵Kioab及其对应的耦合阻尼矩阵Cioab，它们维数为Nτ×Nτ，外层壳体与内层壳体之间的耦合矩阵和阻尼矩阵分别为（Kab）-1和（Cab）-1。

表1 隔振器的刚度和阻尼[10]Tab.1 Stiffness and damping of vibration isolators

综合以上分析，双层壳体齿轮箱的缩聚子结构耦合模型的运动微分方程可以表示为

式中，Fg为双层壳体齿轮箱承受的载荷，xg为齿轮箱振动位移向量，Mg、Kg、Cg分别为齿轮箱的总体缩聚质量、刚度和阻尼矩阵。这些矩阵可以分别表示为

显然，式（2）具有通用性，能够描述双层壳体齿轮箱的模态特性。由于内外壳体子结构是由诸多缩聚点通过弹性耦合连接进行等效，因此广义质量矩阵Mg包含了内外壳体子结构的缩聚点的质量矩阵及其对应结构分布特征，广义刚度矩阵Kg和阻尼矩阵Cg中同样包含内外壳体子结构的缩聚点的质量矩阵和阻尼矩阵，以及隔振器及其对应空间分布的刚度和阻尼矩阵。

2 隔振性能分析的基本方程

2.1 基于能量法的模态解耦率

通过对双层壳体齿轮箱进行模态解耦，在不影响其它自由度方向上的关联性前提下，对隔振效果不好且激振能量大的自由度采取控制措施[20]。因此，探讨双层壳体齿轮箱模态解耦是提高齿轮箱隔振效果一种有效的方法。

根据式（3）可知，若Kioab=0且Cioab=0，内外层壳体将完全解耦。在齿轮箱的结构尺寸不变且忽略隔振器质量下，隔振器刚度对齿轮箱的固有特性影响明显高于隔振器阻尼[21]，因此隔振器刚度是造成内外壳体模态耦合的主要因素。此时内壳体的振动模态由缩聚模型刚度矩阵Kag和隔振器刚度Kioa共同决定，外壳体的振动模态由缩聚模型刚度矩阵Kbg和隔振器刚度Kiob共同决定，即齿轮箱内外壳体存在复杂的耦合振动。双层壳体齿轮箱设计目的是削弱传动系统的啮频振动传递到船舱，能量解耦法能较好地阐述系统在较低频段时刚体模态耦合振动机理。本文将用能量解耦法分析双层壳体齿轮箱的模态耦合机理。

当忽略系统激励和阻尼时，双层壳体齿轮箱缩聚模型的特征值问题可以转化为

式中，ωk和φ（kk=1,2,…,Nτ×Nτ）分别为双层壳体齿轮箱缩聚模型的第k阶固有频率和振型矢量，该振型矢量是按诸自由度中最大幅值归一化获得的。

对于式（4）的双层壳体齿轮箱模态振动问题，其系统的机械能守恒，系统中惯性力做功和弹性力做功总是大小相等、符号相反。因此，从系统广义惯性力做功和广义弹性力做功两个角度阐述模态振动解耦程度是一样的[17，21]，本文将从广义弹性力做功的角度来定义模态示功向量。

若双层壳体齿轮箱系统以第k阶振动时，第m个自由度上所做的功为

所有弹性力在整个系统上做功的最大值为

齿轮箱在第k阶振动的模态示功向量Pmk可由第m个自由度上所做的功与所有弹性力在整个系统所做功的最大值的比值衡量，即

根据模态示功向量Pmk的各个分量的相对大小来判断各自由度耦合程度。实际上，为系统的模态刚度矩阵。

双层壳体齿轮箱内外壳体在第k阶模态振动下所有弹性力在整个系统所做功分别为

由式（7）可得，内壳体和外壳体振动在各自由度下的耦合程度为

式（9）描述了双层壳体齿轮箱在第k阶振动时，各自由度下的能量分布情况。对于双层壳体齿轮箱，期望是以低频的内壳体刚体振动为主。因此，在设计隔振器刚度时应使得Pam（kk=1,2,…6）最大，而Pbmk最小。

然而，被缩聚的双层壳体齿轮箱内壳体子结构具有多个自由度，内壳体的前6阶振型呈现多自由度参与模态振动，使用式（9）仅可获得某个单自由度的内外壳体耦合程度，难以从整体上阐述耦合程度。因此，当内壳体处于第k阶振动时，本文将内壳体子结构所有缩聚节点在3 个平动自由度x（轴向）、y（横向）、（z垂向）及其对应的3个转动自由度R（x绕x轴）、R（y绕y轴）、R（z绕z轴）上的模态示功向量进行叠加，来计算双层壳体齿轮箱的模态解耦率，其表达式为

理论上，若∑PPkj= 1，则说明双层壳体齿轮箱的第k阶模态只有内壳体振动；若∑PPkj= 1 且PPkj= 1，则说明双层壳体齿轮箱的第k阶模态仅表现为内壳体第j方向振动，与其它五个方向完全解耦；若∑PPkj= 1且PPkj＜1，则说明双层壳体齿轮箱的第k阶模态存在内壳体耦合振动。

2.2 模态贡献度

对于一个多自由度的线性定常系统，任一节点响应均可用系统的每阶模态响应线性叠加获得。因此，k个自由度的双层壳体齿轮箱缩聚模型的位移响应为

式中，φ为系统模态振型，φ=[φ1,φ2,…,φk]，φk为系统第k阶振型，与式（4）同含义。qg={q1,q2,…,qk}（Tk=1,2,…,Nτ×Nτ），qk表示第k阶模态振型对系统响应参与程度。

系统的全解耦表达式为

式中，fk为模态坐标中的载荷，fk=。

当双层壳体齿轮箱以简谐振动时，有

式中，qkc为第k阶模态的复模态坐标，fkc为第k阶模态的复载荷。

在激励频率Ω下，双层壳体齿轮箱第k阶模态的贡献量为

每一阶的齿轮箱模态振型在实际响应中的贡献度Qk可以表示为

式（15）可以理解为由齿轮箱的单阶模态引起的振动响应在总振动响应中所占的比重，齿轮箱在某阶的比重越大，则说明齿轮箱的这阶为主导模态，对齿轮箱振动响应越大。

2.3 振级落差和倾斜度

本文以双层壳体齿轮箱的振动加速度响应作为隔振性能考察对象。根据振级落差定义[22]，可得在第i个隔振器处的内外壳体的振级落差为

式中，下标ni和wi分别表示为第i个隔振器对应的内外壳体振动缩聚节点，xˉg为双层壳体齿轮箱的振动复位移。

取所有隔振器处振级落差的平均值作为双层壳体齿轮箱的隔振性能的评价指标，有

式中，Nio为隔振器的数量。

由于双层壳体齿轮箱的内壳体受载荷位置和方向不同，输入端和输出端的隔振器变形有所不同，从而使得内壳体产生倾斜。为了了解双层壳体齿轮箱的内壳体倾斜程度，本文以输入端和输出端在轴承座的振动位移幅值落差比来衡量内壳体倾斜程度，即

式中：下标H和V分别代表内壳体的横向和垂向对应的振动位移变化；δH(V)为内壳体的振动位移幅值落差比；∠δH(V)为内壳体振动位移相位角变形值，它的值越小，则说明内壳体倾斜程度越小，齿轮箱的运行越平稳；xg(Ω)|niH(V)为内壳体输入端的振动位移响应；xg(Ω)|noH(V)为内壳体输出端的振动位移响应。

3 双层壳体齿轮箱的隔振性能分析

3.1 模态解耦分析

由于双层壳体齿轮箱安装于船体上，本文采用弹簧单元表示地脚螺栓刚度，弹簧单元的一端连接到地脚螺栓孔处的缩聚点，另外一端设置为固定约束的边界条件。图4 给出了双层壳体齿轮箱的完全有限元模型[10]和缩聚子结构模型的前六阶固有频率，从图中可以看出，缩聚模型和完全有限元模型的前六阶固有频率非常接近，其最大误差为7.33%。另外，缩聚模型各自由度的前6 阶模态解耦率之和均在97.6%以上，如图5所示。缩聚模型的第1阶的x方向（横向）、第4阶的z方向（垂向）和第5阶的y方向（横向）的模态解耦率最大，其值分别为97.6%、94.9%和95.5%，这表明缩聚模型的第1阶、第4阶和第5阶是平移振动。由于内壳体绕轴向转动时，带动齿轮箱体轴截面上的节点振动，缩聚模型的第2 阶、3 阶和6 阶均有三个自由度（一个转动和两个平动方向）参与振动，这些结果与采用Lanczos 方法计算的双层壳体齿轮箱的完全有限元模型模态响应的结果一致[10]，即双层壳体齿轮箱的前六阶模态振型主要为内壳体独立振动。综合上述表明，双层壳体齿轮箱具有良好的模态解耦特性，且双层壳体齿轮箱的缩聚模型可以代替其实际模型。

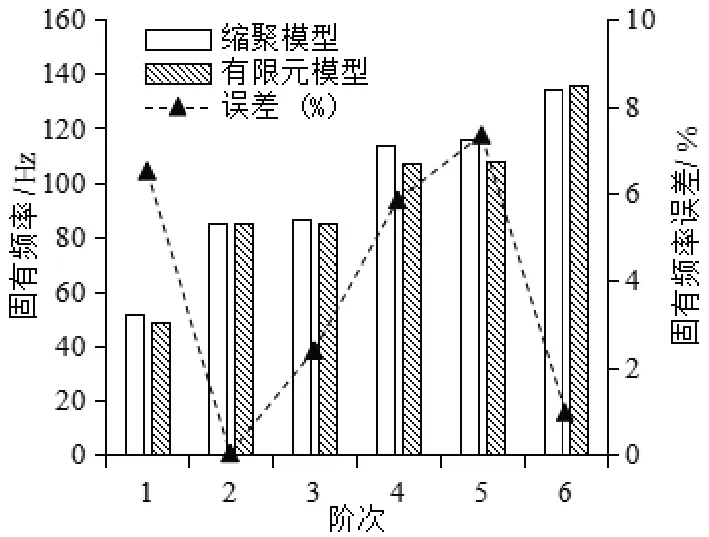
图4 缩聚模型和有限元模型的固有频率Fig.4 Condensation and FEM natural frequencies of the gearbox casing

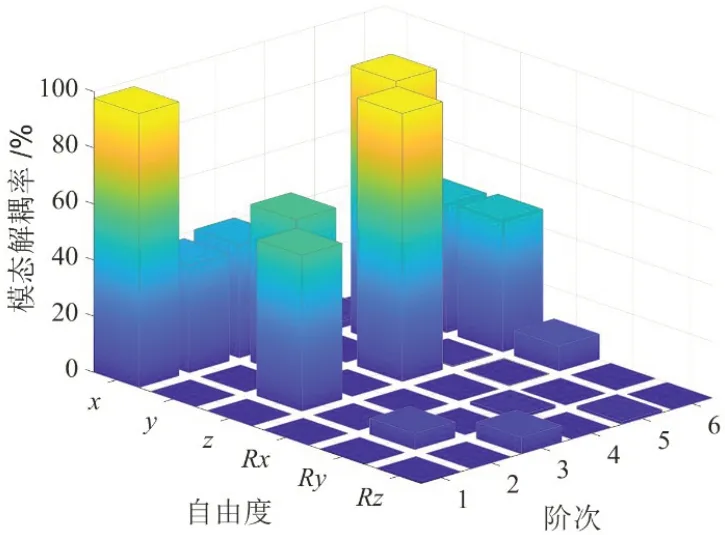
图5 双层壳体齿轮箱的模态解耦率Fig.5 Modal decoupling rate of the double-layer gearbox casing

3.2 模态贡献度分析

通过2.2节模态贡献度的计算方程，可以获得双层壳体齿轮箱的模态贡献度。在计算双层壳体齿轮箱模态解耦率的边界条件基础上，通过在齿轮箱的输入端、输出端以及封闭级行星架缩聚点上施加幅值为1000 N 的激励载荷，并以封闭差动行星齿轮系输入转速3000 r/min 为工况[13]，分析在差动级啮合频率fm1、封闭级啮合频率fm2、及其谐频的激励频率下对双层壳体齿轮箱的前12阶模态贡献度，如图6 所示。双层壳体齿轮箱的第四和五阶模态贡献度占主导地位，第二、三和六阶的模态贡献度小于第四和五阶，它们中最小模态贡献度为13.53%。由于第一阶的模态振型为轴向平移振动，该阶的模态贡献度最大值为0.02%。另外，双层壳体齿轮箱的第十二阶的模态贡献度高于第七至十一阶。第十二阶的模态振型主要表现为输入端输出端轴承座纵向摆动，属于内壳体振动。这些研究结果与3.1节研究结果相对应，即双层壳体齿轮箱前六阶模态振型具有良好的解耦特性，因此齿轮箱前六阶的模态贡献度占主导。

图6 双层壳体齿轮箱的模态贡献度Fig.6 Modal contribution of double-layer gearbox casing with vibration isolators

3.3 振级落差和倾斜度分析

在激励频率1～6000 Hz 范围内，以间隔为0.1 Hz 计算双层壳体齿轮箱的输入端和输出端振级落差，如图7 所示。除了在激励频率347.9～457.7 Hz 范围内的输出端横向振级落差之外，双层壳体齿轮箱的输入端和输出端振级落差均大于零，说明双层壳体齿轮箱具有良好的隔振效果。另外，从图7（b）可以发现，在激励频率347.9～457.7 Hz范围内，齿轮箱垂向的振级落差小于零，这表明隔振器对齿轮箱垂向振动无隔振效果，因此在设计双层壳体齿轮箱时应该避开这频率范围。当激励频率从1.0 Hz 增大到373.1 Hz 时，双层壳体齿轮箱的振级落差急剧下降到最小值；随着激励频率继续增大，振级落差以波动的形式变化。输入端的横向和垂向的最大振级落差分别为27.2 dB和27.3 dB，输出端的横向和垂向的最大振级落差分别为34.2 dB 和30.6 Hz。另外，在不同的激励频率下，输入端的横向和垂向的振级落差存在差异，输出端也是如此。

图7 不同激励频率下的双层壳体齿轮箱振级落差Fig.7 Vibration level difference of double-layer gearbox casing under different excitation frequencies

在激励频率1～6000 Hz范围内，双层壳体齿轮箱的内壳体倾斜程度的变化情况如图8所示。从图中可以看出，当激励频率Ω小于2000 Hz时，内壳体的振动幅值落差比和相位变化值波动比较明显，例如在激励频率Ω=1546.3 Hz时，垂向振动幅值落差比δV=9.60；在激励频率Ω=343.4 Hz时，横向振动相位角变化值为5.97 rad，由此表明当激励频率小于2000 Hz时，应注意齿轮箱的内壳体倾斜程度变化。在设计齿轮箱时，通过降低内壳体的振动幅值落差比和相位变化值，可以提高双层壳体齿轮箱的稳定性。

4 结 论

（1）本文所建立的双层壳体齿轮箱的缩聚模型能够减少其完全有限元模型的自由度。该模型不仅解决了柔性双层隔振系统动力学建模中不相邻的离散质量块在空间上的多向耦合问题，而且在分析隔振器参数对齿轮箱的隔振性能影响方面具有良好的适用性。

（2）本文分别从模态解耦率、模态贡献度、振级落差和倾斜度四个方面对双层壳体齿轮箱的隔振性能进行了分析。研究表明，齿轮箱缩聚子结构模型在平动方向的模态解耦率均在94.9%以上，其模态贡献度主要以二至六阶为主导。当激励频率小于2000 Hz时，对齿轮箱的振级落差和倾斜程度影响较为明显。因此，在提高双层壳体齿轮箱的隔振性能时，既要增大内外壳体的振级落差，又要保证内壳体的良好倾斜程度。