双层三阶多项式拟合的弹道导弹发射点估计方法*
邱明劼,周垂红,汪圣利
(1.南京电子技术研究所,南京 210039;2.中国电子科学研究院,北京 100041)
0 引 言
传统炮位侦校雷达的作战对象以迫击炮、榴弹炮等无动力炮弹为主,此类目标运动轨迹符合抛物线弹道规律,发射点较好预测。但随着作战纵深的日益增加,中近程战术弹道导弹逐步成为炮位侦校雷达的新型作战对象。
与无动力的炮弹不同,弹道导弹的飞行过程可分为主动段和被动段两个部分[1]。由于弹道导弹主动段和被动段运动存在较大差异,为了实现对发射点的精确估计,炮位侦校雷达需针对主动段轨迹而非被动段轨迹进行建模或拟合,从而外推得到发射点位置。然而,由于导弹在主动段的受力情况十分复杂,对于非合作目标,在无先验信息情况下难以准确推断导弹的运动模型,仅能根据理论方法构建近似模型[2-3]。目前对主动段弹道近似建模的方法可以分为两类:一是利用主动段弹道轮廓先验知识进行建模[4]。该类方法通常需要预先积累大量先验数据,难度大且通常只能对已知型号导弹起到较好效果,对未知型号的估计效果差。二是利用通用数学模型对主动段弹道进行拟合[5-7]。由于该类方法不需要积累先验知识,具有可行性强、适用性广的优势特点,因而是目前研究的主要方向。
现有的传统弹道外推算法大多使用各种滤波(如粒子滤波)或平滑算法(如最小二乘)处理雷达测量的位置和速度数据后,直接代入质点弹道方程计算,但在长距离情况下外推误差较大,难以适应弹道导弹的远距离外推需求[8]。文献[9]和[10]分别采用了简单线性模型和重力转弯模型进行弹道拟合,但均无法准确反映主动段运动特性,导致估计精度大幅下降。文献[11]提出了基于时间逆转的反向卡尔曼滤波方法,对于传统炮弹发射点估计效果较好,但仍无法适应弹道导弹主动段运动特征。
本文提取弹道导弹主动段在垂向和射向两个方向的运动特征,将发射点零时刻估计作为发射点估计的中间过程,提出了一种基于双层拟合的发射点估计方法。该方法首先利用发射时间和导弹垂直位移之间的关系,利用三次多项式迭代估计导弹发射零时,然后利用时间与射向之间的物理关系,估计出导弹发射点位置。本文所提方法估计参数数量少,计算简单,定位误差较传统方法降低了50%以上,具有重要军事应用价值。
1 弹道导弹运动轨迹仿真
通过正向设计,精确仿真弹道导弹轨迹是进行弹道运动轨迹研究和发射点估计的重要前提。表1给出了弹道导弹的飞行阶段及其受力情况,以此为理论基础进行轨迹仿真[12]。

表1 弹道模型的分段及其受力情况
假设弹道导弹关机点以后仅受到重力的作用,导弹目标的位置为p=[px,py,pz]T,速度为v=[vx,vy,vz]T,则依据圆球体地球模型建立的弹道导弹运动轨迹可以表示为
(1)
式中:aT为推进力产生的加速度;aD为空气阻力产生的加速度;aG为地心引力产生的加速度;aC为科氏力和离心力产生的加速度。aT,aD,aG,aC构成了弹道目标的加速度[13]。

(2)

(3)
设ρ(h)是空气密度函数,ρ0=1.22 kg/m3,k=0.141 41×10-3m-1,h(t)为t时刻目标海拔高度,v(t)为t时刻目标速度,uv是单位向量,m(t)为t时刻目标质量,cD(v)是阻力系数,S是目标体与其速度方向的截面积,则空气阻力加速度可近似表示为
(4)
ρ(h(t))=ρ0e-kh(t)
(5)
(6)
设ω=[0,0,ω]′是地球自转角速度矢量,则科氏力和离心力产生的加速度为
(7)
综上所述,根据式(1)~(7),可得到弹道导弹主动段运动模型为

(2ωvy+ω2px)
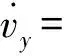
(-2ωvx+ω2py)
(8)
在被动段没有了推力,运动模型变为

(2ωvy+ω2px)
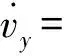
(-2ωvx+ω2py)
(9)
根据式(8)和式(9)即可通过正向设计的方式构建出弹道导弹的仿真运动轨迹,用于对本文所提方法进行仿真验证。
2 主动段双层拟合方法
图1为主动段双层拟合方法的流程图,主要包括拟合坐标系建立、发射零时刻估计、主动段水平位移拟合和发射点估计及误差计算4个步骤。
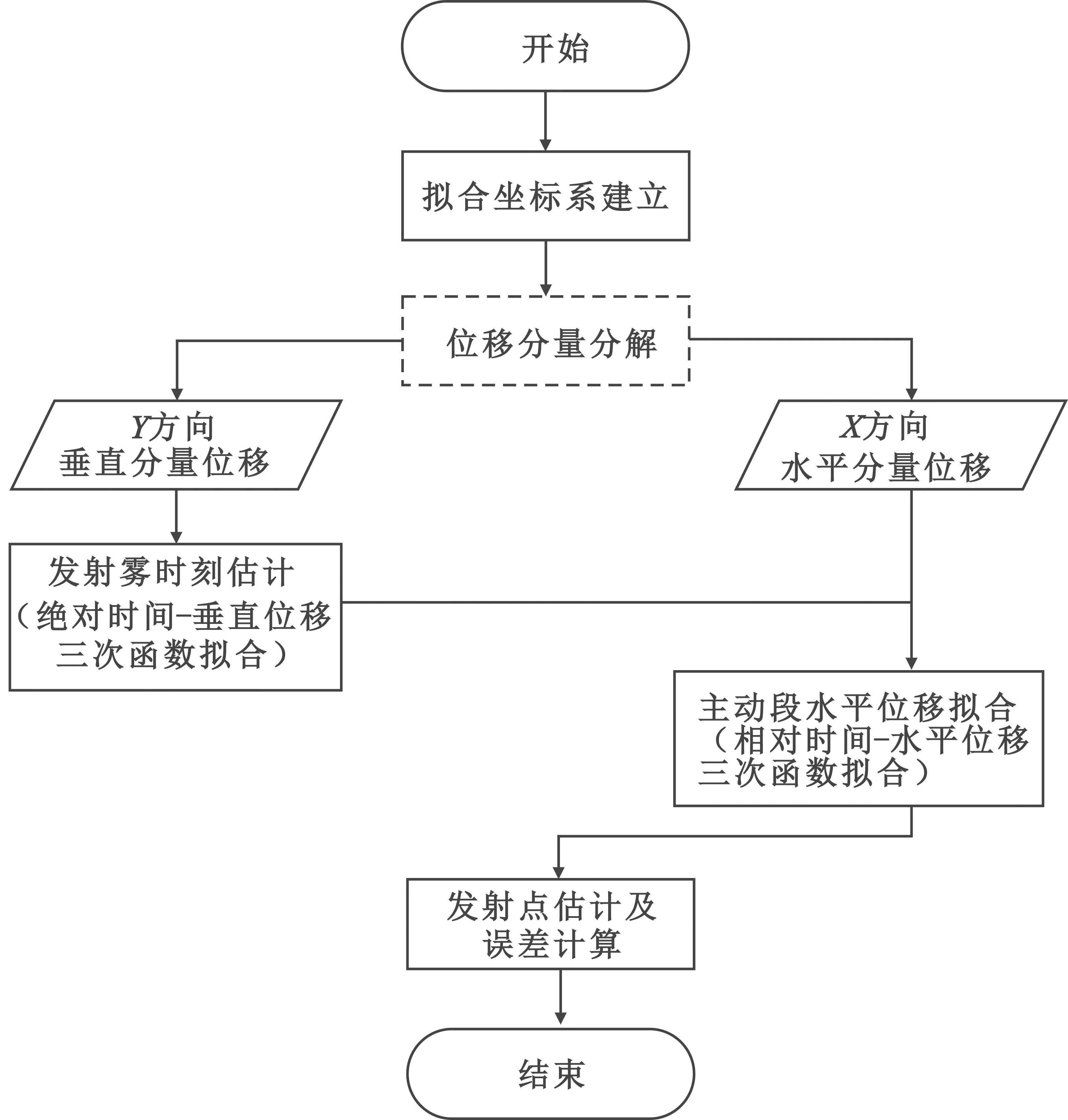
图1 主动段双层拟合方法流程
2.1 拟合坐标系建立
弹道曲线是在发射坐标系O′X′Y′Z′下进行描述的,但由于雷达无法提前知悉非合作目标的发射点位置,仅能通过探测数据拟合发射坐标系,从而在这个坐标系下进行发射点估计。在本文中将雷达依据观测数据建立的坐标系称为拟合坐标系。
拟合坐标系是以雷达观测到的第一个导弹位置点在水平面上的投影作为原点O,以雷达观测到的主动段数据在水平面上的投影的最小二乘拟合结果作为X轴,垂直于水平面竖直向上为Y轴,如图2中虚线坐标系OXYZ所示。
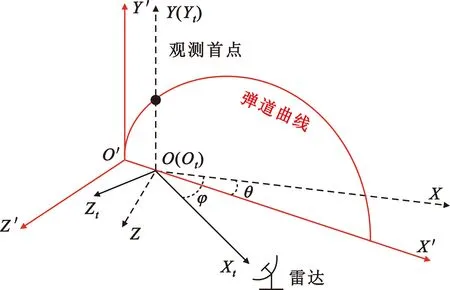
图2 拟合坐标系OXYZ、发射坐标系OX′Y′Z′和临时坐标系OtXtYtZt示意图
为了建立拟合坐标系,需要首先依据雷达的部署位置,首先建立临时坐标系OtXtYtZt,然后再通过坐标旋转的方法,将其旋转至拟合坐标系下。
下面具体阐述拟合坐标系建立的过程:
1) 以雷达观测到的第一个弹道导弹轨迹点在地面上的投影为临时坐标系原点Ot,其与雷达位置之间的连线为临时坐标系Xt轴,垂直地面向上为临时坐标系Yt轴,并根据右手法则确定临时坐标系Zt轴,则观测到的临时坐标系下的轨迹点集合为Pt={[0,0,zt0]T,[xt1,yt1,zt1]T,[xt2,yt2,zt2]T…}。
2)对轨迹点集合Pt在XtOtYt平面上的投影进行一阶函数最小二乘拟合,求得各轨迹点Yt轴坐标关于Xt轴坐标的关系,即ytn=f(xtn)=axtn+b,其中a和b是最小二乘拟合得到的拟合参数。
3)根据求得的参数a,得到临时坐标系OtXtYtZt与拟合坐标系OXYZ之间的角度偏差φ=arctana,然后使用旋转矩阵将轨迹点坐标进行转换,即
(10)
得到在拟合坐标系下的轨迹点集合P={[x0,y0,z0]T,[x1,y1,z1]T,[x2,y2,z2]T…}。
通过上述步骤,即可将坐标由雷达初始探测得到的临时坐标系转换至拟合坐标系中。在后续的两次三阶多项式拟合过程中,均认为弹道仅在拟合坐标系的XOY平面内运动,在可以将导弹在三维空间中的位移情况简化为在弹道平面内的二维运动,简化弹道估计的同时完成了位移分量的分解,得到在X方向的水平位移和Y方向的垂直位移两个分量。
但从图2中可以看到,拟合坐标系Y轴与导弹发射坐标系的Y′轴方向相同,但X轴和Z轴均与实际发射坐标系的X′轴和Z′轴存在一个角度偏差θ,这是由于实际弹道主动段在Z'方向的运动以及雷达的观测误差影响所导致。在仿真条件下,可以通过对无误差的仿真弹道在X′O′Z′平面投影的坐标进行一次多项式拟合,从而与拟合坐标系下的轨迹点集合拟合结果进行比较,根据两者拟合后一次函数的斜率求得角度偏差θ。但在实际作战条件下,将无法获取这个角度,这将使得沿着拟合坐标系X轴进行外推的方向与实际弹道运动方向之间存在偏差,而这正是发射点估计的误差来源之一。
2.2 发射零时刻估计
在2.1节建立的拟合坐标系中,当忽略弹道轨迹在Z轴方向上的运动时,可认为zTn≡0(n=1,2,3…),则导弹绝对发射时刻TS的弹道点坐标可表示为(xTS,yTS,zTS)=(xTS,0,0),Ti时刻的弹道点坐标为(xTi,yTi,0)。通过弹道导弹运动模型仿真结果和大量实测数据可以看出,导弹主动段在垂直方向的位移量yTi和水平方向的位移量xTi-xTS均为随相对发射时间ti=Ti-TS(i=1,2,3…)单调增长的平滑曲线。
尽管TS和xTi-xTS均为未知量,但绝对发射时间Ti和在Y轴方向上的位移量yTi均直接已知,因此可以假设TS=0 s,则ti=Ti,通过三阶函数最小二乘拟合的方法,拟合出时间ti与yti的函数关系yti=g(ti)。考虑到发射的导弹在相对发射时间0 s以前,其高度方向位移应始终等于0,而在相对发射时间0 s之后,高度方向位移应当始终大于0,因此在进行函数拟合时,基于上述事实对拟合过程进行约束:当ti≤0时,主动段Y方向位移均等于0;当ti>0时,主动段Y方向位移均大于等于0,即
(11)
从而使得拟合得到的三次函数曲线系数快速收敛,且不会因为过拟合导致外推趋势发散。
根据上述两个事实可知,当拟合出的三次函数曲线最靠近初始观测值的零点坐标越接近于0时,即t0越接近于0 s,所拟合出的函数应当越符合事实情况。因此,在拟合出时间-垂向位移函数曲线后,首先使用梯度下降法求出离第一个观测点最近的拟合曲线零点坐标(tz,0),然后将发射零时刻加上tz与优化速率η乘积代表的时间修正量Δt,对TS进行修正。该过程也可等效为将所有观测数据时间Ti减去由tz与优化速率η乘积代表的时间修正量Δt,对Ti进行修正。
(12)
之后重复利用新的相对时间ti与位移yti进行拟合、求零点、修正,使得逐次求得的三次函数零点tz逐步与0 s接近。当拟合曲线零点坐标tz小于所设定的阈值ttreshold,即可认为在满足上述约束条件下,时间-垂向位移拟合曲线与真实弹道在Y方向的曲线吻合,从而确定了每个轨迹点的相对时刻ti。
发射零时刻估计的具体过程如下:
1) 假定TS=0,利用每个轨迹点的绝对时刻Ti和高度方向位移yti进行三次函数的最小二乘拟合,得到拟合函数
2) 使用梯度下降法,从第一个观测到的轨迹点开始,求出离其最近的拟合曲线零点坐标(tz,0)。
3)若|tz|≤ttreshold,即认为此时的TS已经足够接近真实时间,拟合得到的曲线与实际情况吻合,得到拟合结果g(ti);|tz|>ttreshold,则使用优化速率η乘以tz得到时间修正量Δt。
4) 将TS加上时间修正量Δt,重新求得每个轨迹点的相对时间ti=Ti-TS。
5)重复步骤1)~3),直至得到拟合结果g(ti)。
2.3 主动段水平位移拟合
在拟合坐标系中,发射点位置估计实际上已经被转化为求取相对时间t0时刻水平X方向位移量的问题。在2.2节中已经将TS收敛至真实绝对发射时间,从而使得发射点的相对发射时间t0≈0 s,进而进行第二次三次函数的最小二乘拟合。此时将各轨迹点的相对发射时间ti作为自变量,以轨迹点的X方向位移作为应变量进行最小二乘拟合,即可得到导弹在水平面投影上的时间-水平位移拟合结果xTi=h(ti)。
在进行三次函数拟合之前,同样需要考虑如下的约束条件。由于是采用三次多项式对X方向的位移进行拟合,而对位移求导即可得到对应方向上的运动速度,因此在X方向上的速度应为二次多项式形式。考虑弹道导弹通常采用垂直发射,在X方向上初始速度为0,因此首先对时间-速度曲线构建无常数项的二次多项式拟合模型:
vti=k(ti)=avti2+bvti
(13)
接着再对上式进行积分即可得到X方向位移关于时间Ti的三次多项式模型:
xti=p(ti)=axti3+bxti2+cx
(14)
利用该三次多项式模型对数据进行最小二乘拟合,即可得到主动段水平位移关于发射相对时间的具体表达式。由于这次拟合没有相关的事实约束条件,因此其拟合精度与t0≈0 s的准确性密切相关。
2.4 发射点估计及误差计算
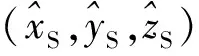
由于拟合坐标系中的XOY平面是对三维发射坐标系中X′O′Y′平面的近似估计,两者之间存在角度偏差θ,为了计算发射点估计结果的误差,需要将在发射坐标系中的真实发射点位置坐标根据角度θ变换至拟合坐标系下。
根据2.1节所述,利用一次多项式拟合求得拟合坐标系和真实发射坐标系之间的夹角θ后,设发射点真实位置在发射坐标系中的坐标为(xT′,yT′,zT′),雷达观测首点在发射坐标系中的坐标为(xF′,yF′,zF′),则发射点真实位置在拟合坐标系中的坐标(xS,yS,zS)可表示为
(15)
从而得到最终的发射点定位误差ε为
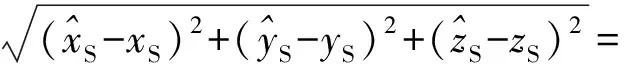
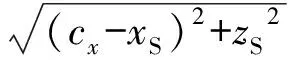
(16)
当雷达与导弹发射点之间距离为R时,定位精度P定义为定位误差除以侦察距离:
(17)
3 仿真实验及结果分析
3.1 仿真条件
仿真过程采用搭载主频为3.00 GHz的i5处理器的计算机进行,仿真语言为Matlab语言。
仿真时,首先根据式(8)和式(9)表示的弹道导弹主动段和被动段运动模型,调整参数生成射程200~1 000 km的近程战术弹道导弹轨迹,然后设置雷达位置并生成雷达观测数据。结合实际作战场景情况,假设炮位侦察雷达部署于导弹射向方向,且距离发射点位置300 km,雷达探测角度精度0.1°、距离精度100 m,探测仰角范围为2°~25°,仿真场景如图3所示。
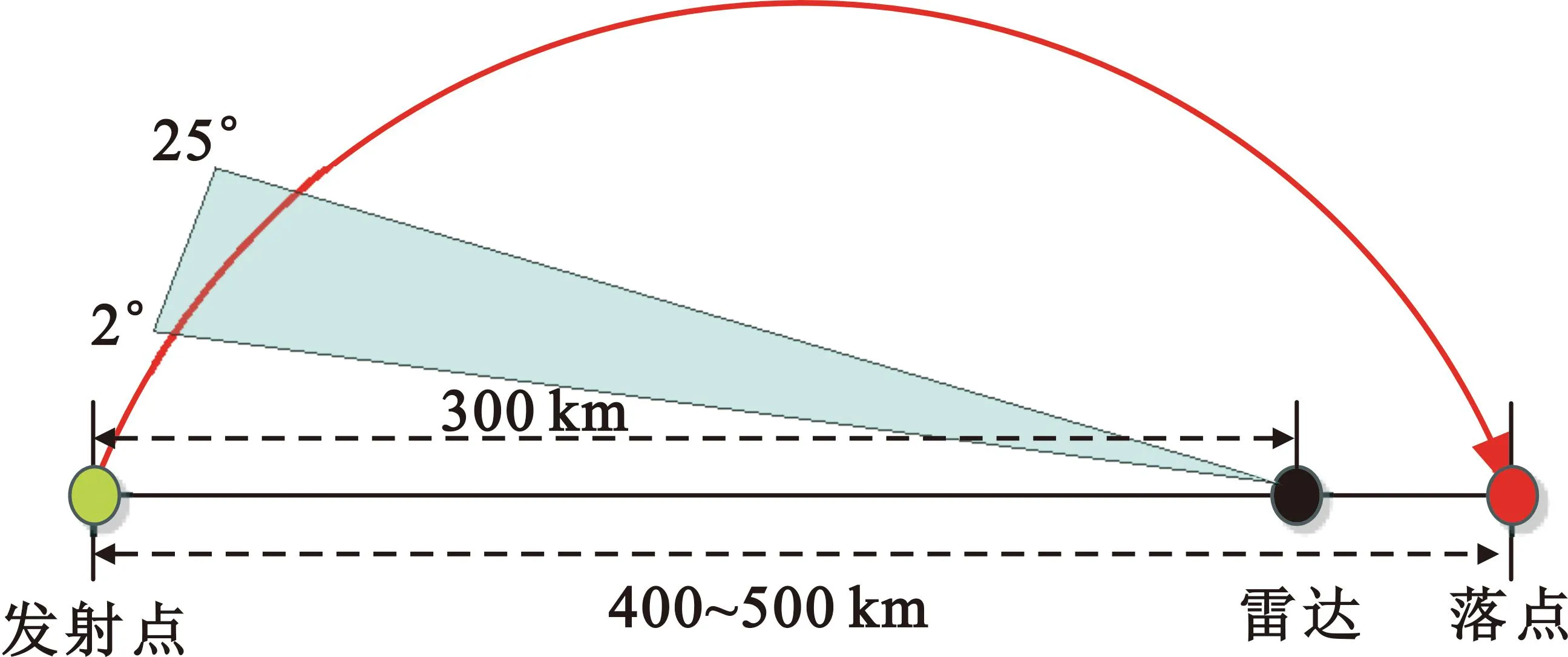
图3 仿真实验场景设置图
考虑地球曲率影响和雷达仰角探测范围,从仿真生成的弹道中选择出可被雷达观测的弹道弧段,并添加雷达测量误差。接着分别使用常规弹道外推的定轨方法[15],和本文提出的主动段双层拟合方法进行发射点位置估计,并多次添加雷达误差进行蒙特卡罗仿真,统计发射点精度结果。单次仿真流程如图4所示。
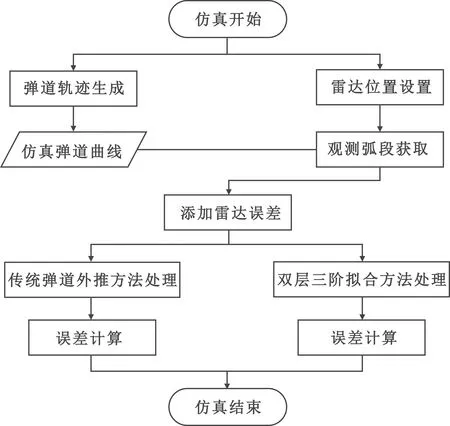
图4 单次仿真实验流程
本文所提方法中提到的时间修正量阈值参数Ttreshold和优化速率参数η,在所有的仿真过程中均取2和0.5,发射时间TS初始值设置为-100 s,则相对时间t0=100 s。
3.2 仿真分析
根据弹道导弹运动模型生成的某条弹道轨迹如图5所示,并以此弹道轨迹为例进行精度分析。该弹道在发射坐标系下各方向的位移与时间的关系曲线如图6所示,其中红色曲线部分即为弹道导弹主动段轨迹,黑色曲线部分为被动段轨迹。
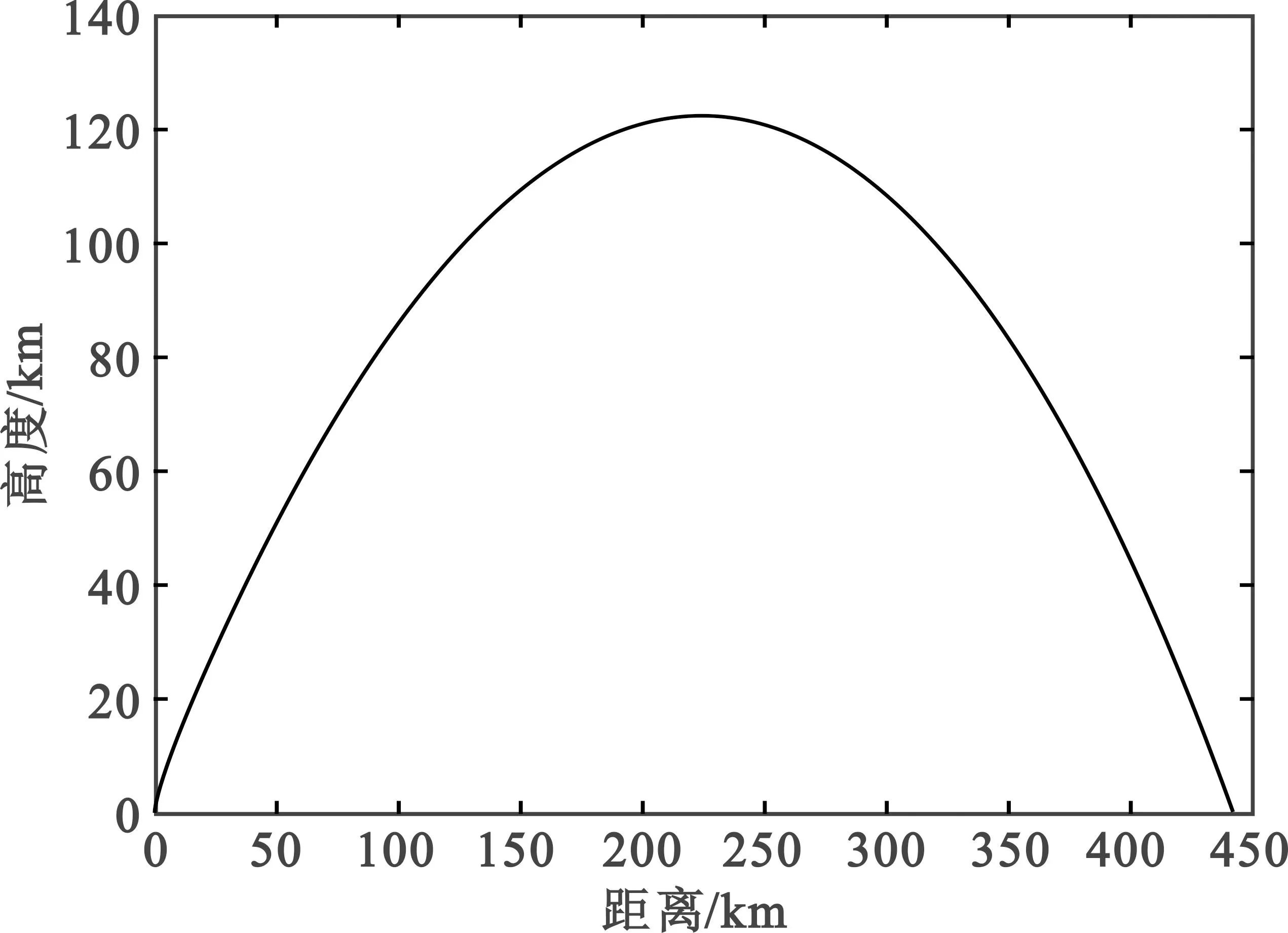
图5 某条仿真弹道轨迹
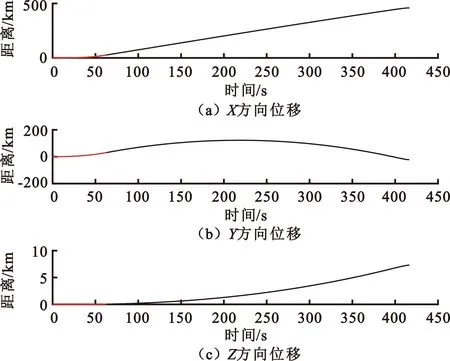
图6 某条仿真弹道时间-位移分量曲线
选取添加测量误差后的主动段数据,利用主动段双层拟合方法则雷达可观测到的弹道轨迹如图7所示。

图7 雷达可观测弹道轨迹
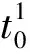
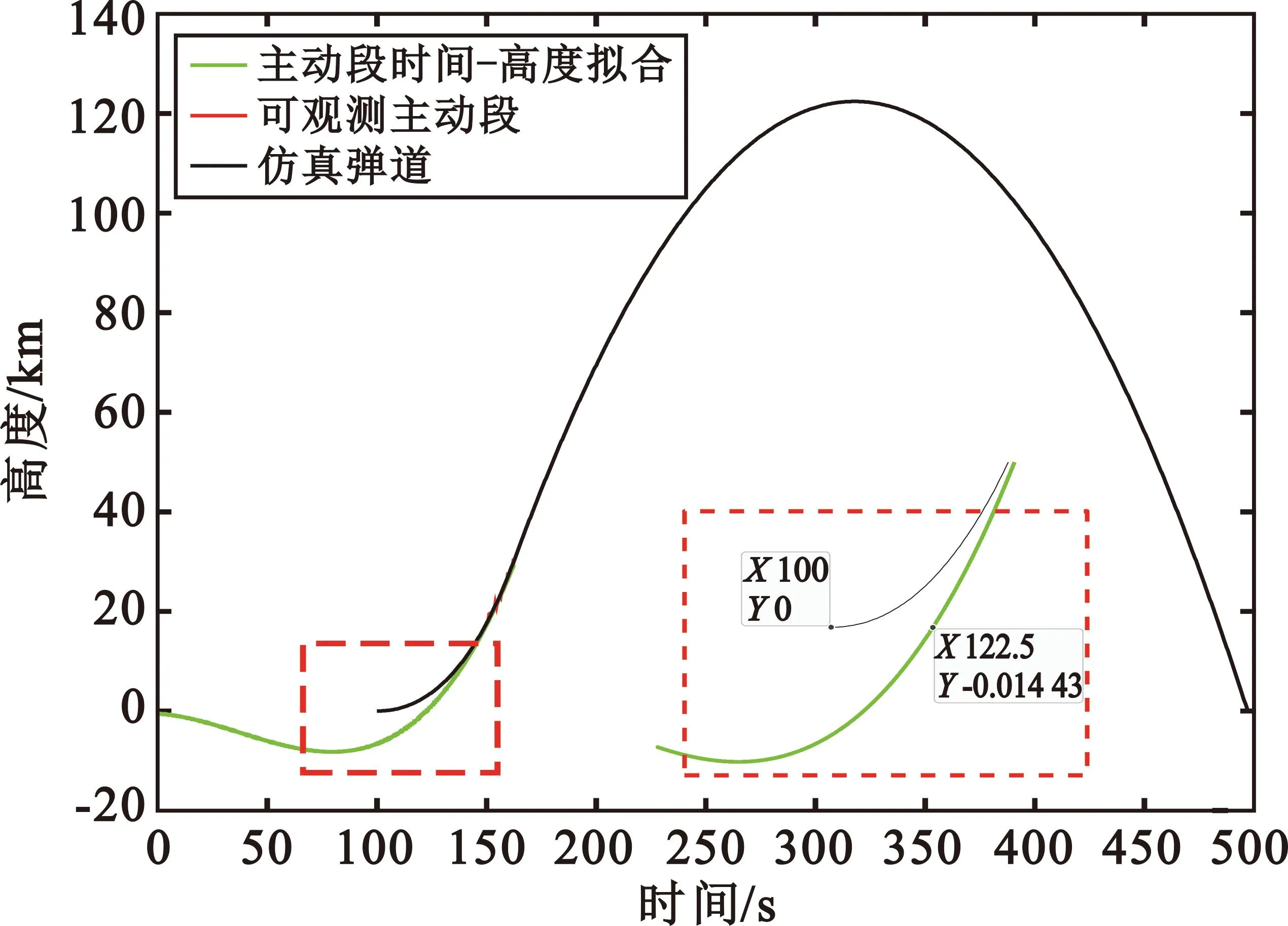
(a)时间-位移拟合第1次迭代结果
将第一层三阶拟合后得到的Ti用于和拟合坐标系中的X方向水平位移进行第二层三阶拟合,得到拟合结果如图9中绿色曲线所示。
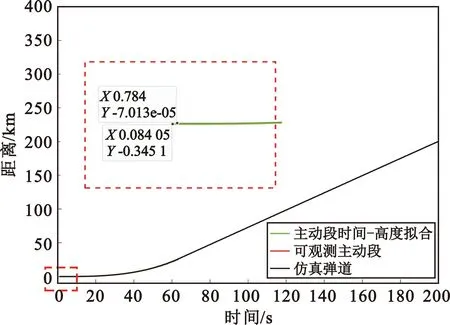
图9 主动段时间-水平位移三阶函数拟合结果
从图9中可以看出,在构建的拟合坐标系下,发射点位置估计结果为(-345.13,0,0)m。通过坐标变换,真实发射点位置转换至拟合坐标系下的坐标值为(-70.13,0,-40.51)m,根据式(15)可得定位误差为277.97 m,并根据式(16)计算得到本次仿真定位精度为277.97/300000=0.09%。
按照上述实验方法,共仿真生成10条弹道,其中前7条弹道为单级助推导弹弹道,后3条为二级助推导弹弹道。每条弹道采用传统弹道导弹定轨方法和本文方法分别进行100次蒙特卡罗实验,并使用2.4节所提的精度计算方法进行统计,得到发射点定位误差和精度情况如表2所示。从表2的结果可以看出,在仿真条件下,传统利用定轨方法对具有一级和二级助推的仿真弹道发射点定位精度在0.7%~1.4%之间,而本文所提方法对发射点的估计精度可达到0.6%以内,定位误差相比优于传统方法降低50%以上。
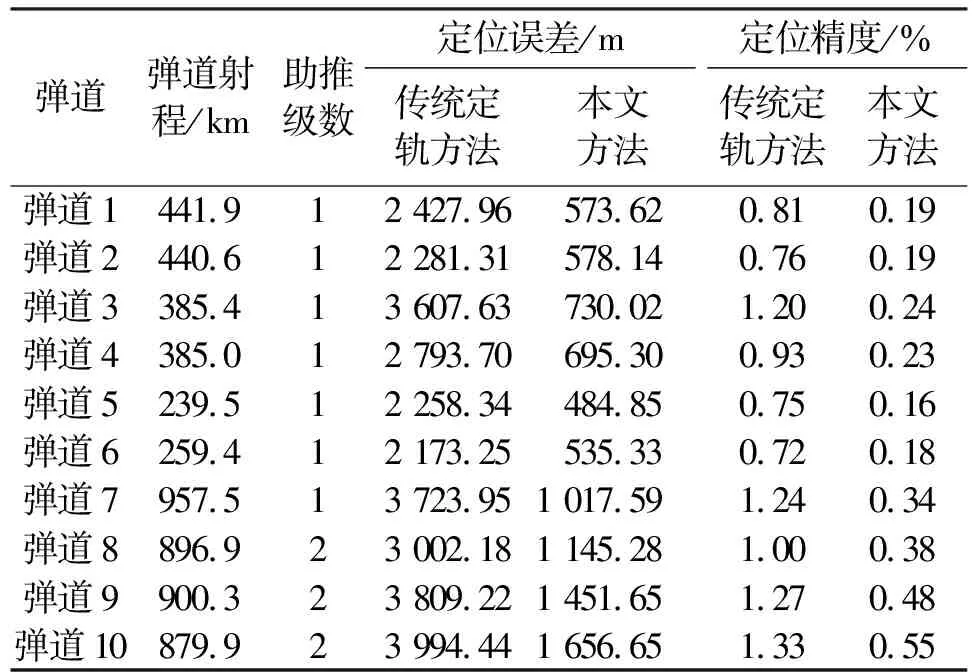
表2 传统弹道外推方法与本文方法定位误差对比
接着进一步考虑不同雷达探测精度对本文算法的影响。对于现有雷达,角度精度通常在0.5°以内,且对于远距离探测时角度精度带来的测量误差远大于距离精度影响,因此仅分析雷达角度精度对定位精度的影响。
分别选取具有一级助推和二级助推的弹道1和弹道8作为雷达测量精度对定位精度影响分析的实验弹道。假设雷达测角精度不超过0.5°,每0.01°设置一个精度采样间隔,生成雷达测量误差与理论弹道轨迹叠加,并使用本文方法在每个测角精度条件下进行100次蒙特卡罗实验,统计对两条弹道的发射点定位精度,结果如图10所示。
从图10可以看出,对于具有一级助推和二级助推的弹道导弹轨迹,其发射点定位精度随着雷达精度变差而逐步变差,但即使在雷达测角精度达到0.5°的情况下,使用本文算法得到的定位误差也仅与测角精度0.1°情况下使用传统方法得到的定位精度相近,从而充分说明本文所提方法可有效指导我方部队遂行精确对地打击任务,具有明显先进性。同时,本文算法在3.1节所述的仿真条件下,单次仿真运行时间约为0.03 s,满足发射点解算的实时性要求,具备良好的工程可实现性。
4 结束语
本文提出了一种基于主动段双层拟合的弹道导弹发射点估计方法,利用三阶函数拟合弹道导弹轨迹的时间-高度曲线,较准确地估计出相对发射时刻后,再利用相对发射时间与水平距离位移进行第二次三阶函数拟合,进而得到发射点的位置估计结果。在仿真实验条件下,将本文方法与传统弹道外推方法进行了对比,充分验证了方法的有效性。
本文所提方法能够良好处理具有一级和二级助推的弹道导弹发射点估计任务,但当主动段的运动状态更加复杂时,其轨迹将难以使用简单多项式函数进行拟合逼近,从而导致较大预测误差。随着机器学习和神经网络的广泛应用,其在轨迹预测方面已有许多学者开展研究。由于神经网络具有对复杂非线性系统的良好逼近能力,将神经网络的方法引入到弹道导弹发射点估计中提升定位精度可作为后续进一步研究的方向。

