一种模型驱动的深度学习OFDM接收机*
刘 檬,卢 敏,胡 娟,李卓敏
(江西理工大学 理学院,江西 赣州 341000)
0 引 言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术因其优异的性能被用于无线通信标准[1],但传统的OFDM系统依赖于数学模型,而复杂的信道环境很难用数学公式表达。
近几年,深度学习(Deep Learning,DL)方法因具有很强的非线性能力,能够较好地解决通信系统中描述不准确的问题,在通信系统中得到了广泛的应用,包括信号辨识[2]、信道估计[3]、信道解码[4]、信号解调[5-8]等方面。文献[9]提出以神经网络构建端到端的通信系统,解决了传统算法不能实现全局优化的问题,但该方法需要同时训练发送端和接收端,训练难度较大。文献[10-11]针对训练难度大的问题,提出了数据驱动的方法,采用全连接神经网络和卷积神经网络实现信息接收。此方法结构简单,误比特率性能较佳,但需要大量的训练数据样本且时间和空间复杂度高。为了降低模型复杂度,文献[12-13]提出了一种模型驱动的接收机,其结合无线通信领域的专家知识,通过传统算法初始化神经网络输入,极大地提升训练效率,减小数据依赖,降低接收机整体复杂度,但是在复杂信道下接收机的抗噪声性能有待提高。
基于以上分析,针对深度学习的OFDM接收机网络参数大、收敛速度慢、计算复杂度高的问题,本文采用深度学习方法,结合专家知识和多种神经网络,构建一种模型驱动的无线接收机模型,即FBLTNet(Fully Connected,Bi-LSTM and Transformer-encoder Neural Network)。该接收机分为信道估计和信道检测两个模块,以最小二乘(Least Squares,LS)信道估计算法和最小均方误差估计(Minimum Mean Square Error,MMSE)信号检测算法初始化神经网络的输入,使得模型的输入具有物理意义,降低模型的复杂度以及提高解调性能。在信道估计模块中,以全连接神经网络(Fully Connected Deep Neural Network)替代线性插值部分,实现信道状态信息(Channel State Information,CSI)的估计。在信号检测模块,由深度自注意力网络编码器(Transformer-encoder)[14]与双向长短期记忆网络(Bidirectional Long Short Term Memory,Bi-LSTM)[15]组合的网络实现信号比特流的恢复。
本文将从噪比性能、调制方式、导频数量、循环前缀角度,对比分析FBLTNet接收机、传统接收机和现有的深度学习接收机。
1 系统模型
OFDM无线通信系统包括发射机、信道和接收机,如图1所示。系统发射端将输入的二进制数据序列调制为发射符号序列,插入导频符号形成完整的OFDM发送符号,符号经过离散傅里叶逆变换(Inverse Discrete Fourier Transformation,IDFT)转换为时域信号,接着加入循环前缀(Cyclic Prefix,CP),以减轻由无线信道的延迟扩展引起的符号间干扰(Inter-symbol Interference,ISI),形成完整的时域OFDM信号。
OFDM接收机中,由于信号在传输过程中,发送和接收是异步的,即可能出现发射端的信号在接收端收不到或者接收不完全的情况。为了使得数据能够正常工作,不破坏子载波之间的正交性,接收端在快速傅里叶变换(Fast Fourier Transformation,FFT)变换之前,发射机和接收机必须进行同步操作,之后去除CP,然后再执行FFT变换,将接收信号Y(k)表示为第k个子载波的接收信号,接着进行信道估计、信号检测和星座映射解调。
信号通过一个频率选择性衰落多径信道的脉冲响应表示为
(1)
式中:M为多径条数;τi为第i路信号的时延;h(i)为第i路信号的幅度衰减因子。在符号正确同步的情况下,接收端的采样信号为
(2)
式中:Ts为采样周期;n(nTs)为采样的高斯白噪声。当用循环卷积代替信号与信道的线性卷积时,对接收到的信号做快速傅里叶变换后解调出的频域信号为
Yi,k=Xi,k*Hi,k+wi,k
(3)
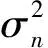
(4)
式中:Xi,k(P)和Xi,k(D)分别表示第k个子载波中的导频和发射符号。Xi,k(P)在接收端是已知的,用于信道估计,而Xi,k(D)在接收端是未知的,需要根据接收到信号和估计信道进行检测。
基于人工智能(Artificial Intelligence,AI)的接收机,用神经网络取代传统接收器中的信道估计和信号检测,将大量的无线信号作为神经网络的输入,比特流信号作为输出,通过随机梯度下降算法训练所有参数。下面将详细介绍本文提出的FBLTNet接收机。
2 接收机设计
2.1 FBLTNet接收机
将接收端接收到的时域信号YD∈M×N,经过信道的导频Yp∈和接收端已知的原始导频Xp∈作为输入数据,通过所提出的FBLTNet接收机获得恢复的比特流信号,其数据流如图2所示。
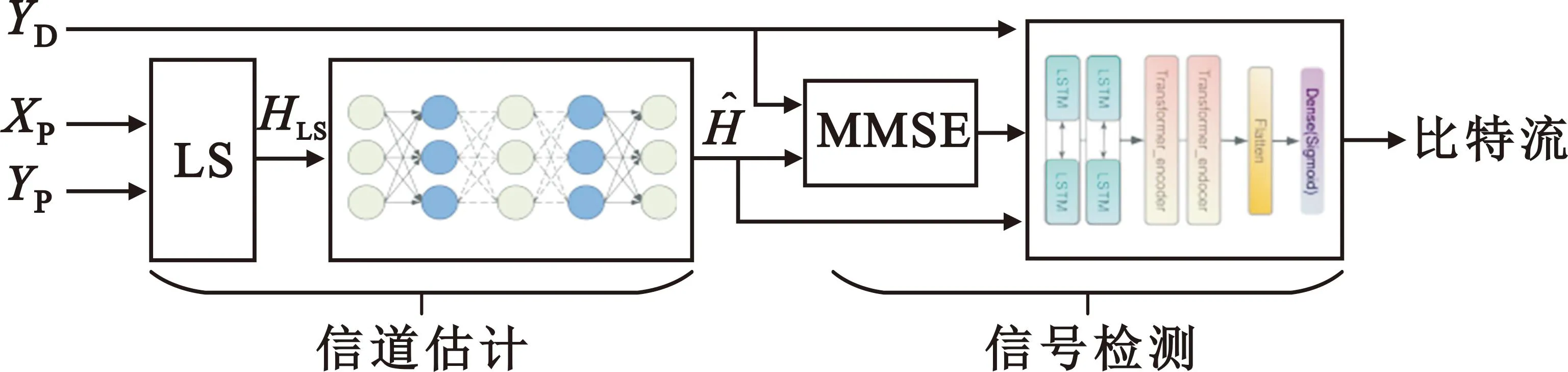
图2 FBLNet接收机数据流图
2.1.1 信道估计
信道估计的作用是估计出信道状态信息矩阵。导频辅助信道估计采用LS算法,通过利用导频估计导频位置的信道响应,表示为
HLS=Yp/Xp,HLS∈M×N
(5)
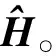

图3 信道估计网络
2.1.2 信号检测
信号检测先利用传统检测算法初始化神经网络的输入,再通过信号检测神经网络(简称SD网络)恢复比特流信号,如图4所示。
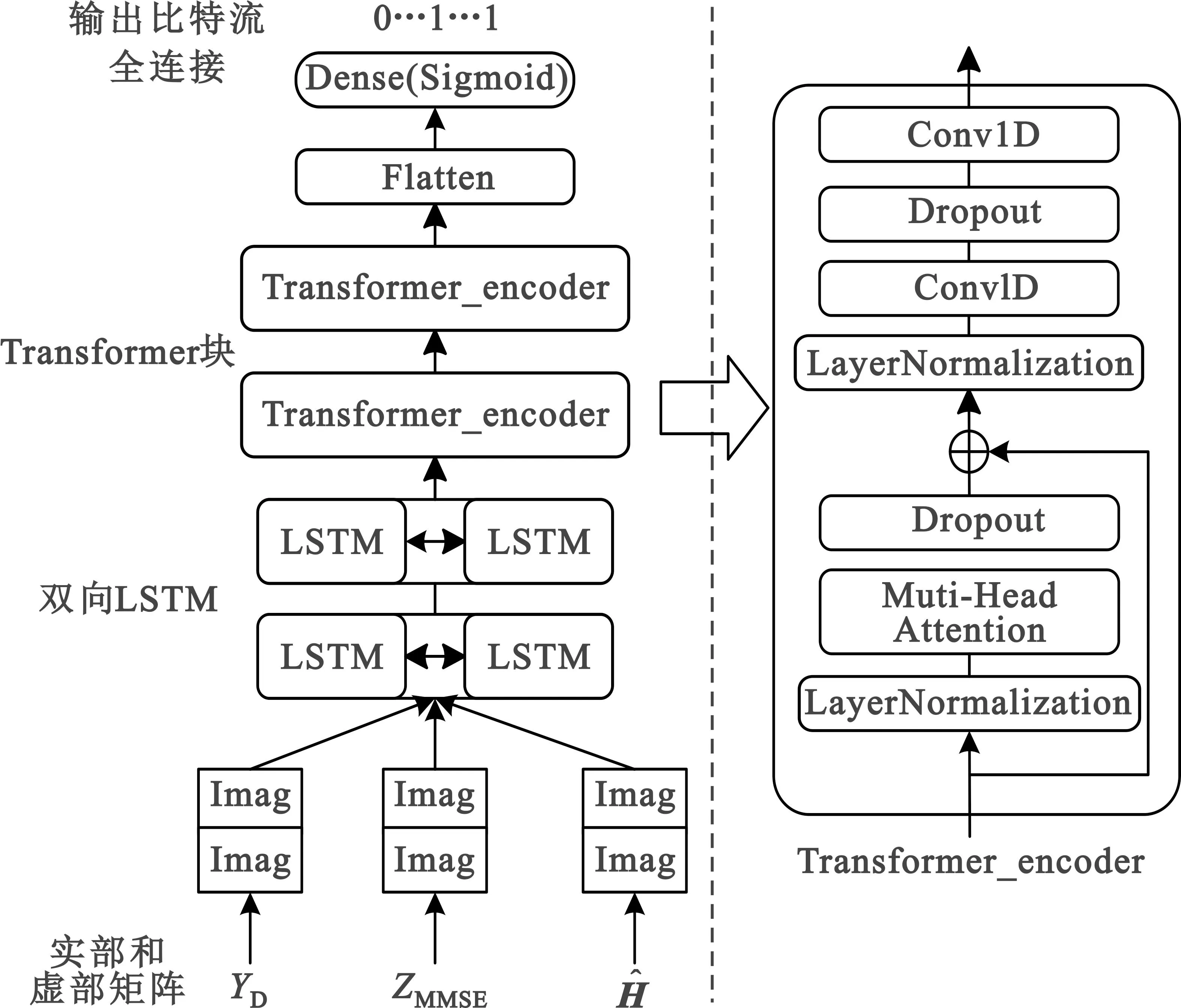
图4 信号检测网络结构数据流图
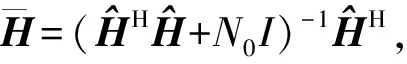
(6)
由于此时信号是复数信号,在输入神经网络前提取YMMSE∈M×N,YD∈M×N和M×N3个复数特征矩阵复数的实部和虚部,合并成6列的实数矩阵,则SD网络的输入矩阵G∈M×6N表示为
(7)
式中:Re{·}表示取复数值的实部;Im{·}表示取复数值的虚部。用WSD表示SD子网权重,bSD表示该神经网络偏置,则SD子网的输出σ表示为
σ=WSD×G+bSD
(8)
2.2 信道估计网络
CE网络由3层的批量归一化(Batch Normalization)和两层的全连接层(Dense)组成,全连接层的神经元个数分别是256和128;采用ReLU激活函数;网络结构见图3。

(9)
2.3 信号检测网络
SD网络结构如图4所示,由两个双向长短期记忆网络(Bi-LSTM)、两个深度自注意力编码器网络(Transformer-encoder)及一个全连接网络组成。
2.3.1 Bi-LSTM
使用ReLu激活函数,神经元个数64,主要用于信号序列上下文的学习。Bi-LSTM为两个单向LSTM网络的组合,其中一个LSTM网络进行数据的正向预测,另一个LSTM网络进行反向预测。LSTM网络中有若干个LSTM单元,每个单元由输入门it、遗忘门ft、输出门ot、记忆单元ct和隐藏层矢量lt组成,并且每个单元参数共享,即每个时间步上神经网络的参数都一样。则单个LSTM网络结构的数学描述如下:
it=σ(bi+Uixi+Wilt-1)
(10)
ft=σ(bf+Ufxt+Wflt-1)
(11)
ct=ft⊙ct-1+it⊙σ(bc+Ucxt+Wclt-1)
(12)
ot=σ(bo+Upxt+Wolt-1)
(13)
lt=ot⊙tanh(ct)
(14)
式中:Ui,Wi,Uf,Wf,Uc,Wc,Uo,Wo∈d×d为网络中的权重矩阵;bi,bf,bc,bo∈d为网络的偏置,权重和偏置在训练学习过程中确定下来;⊙表示元素乘法;σ为sigmoid函数;d表示输入序列维度。每个时间步LSTM网络的输出lt和隐藏层更新变换公式可以简化为式(15)和(16):
lt=LSTM(lt-1,xt,Θ)
(15)
(16)
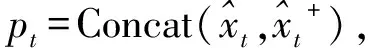
(17)
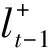
2.3.2 Transformer-encoder
Transformer-encoder的作用主要为了加强信号序列学习的深度,提取序列的特征,解决序列中长期依赖问题,包含注意力机制和残差结构,分别为层归一化(LayerNormalization)、多头注意力(Muti-Head Attention)、失活(Dropout)和一维卷积(Conv1D)。LayerNormalization表示层归一化函数,其作用是将输入的特征数值进行规范化转换,使得整个网络的计算过程数值更稳定,训练网络收敛速度更快。多头注意力将原输入向量映射为多个不同的查询矩阵Q、键矩阵K和值矩阵V的三元组,然后对每个三元组分别使用点积注意力机制进行计算,最后将不同三元组计算得到的输出进行拼接得到表达能力更多样的新特征向量,数学表示如下:
(18)
Mutihead(Q,K,V)=Concati=1,…,n(headi)Wp
(19)
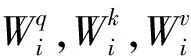
Dropout层作用是通过在训练期间随机丢弃网络节点,可以使用单个模型来模拟具有大量不同的网络架构,是一种计算低成本且非常有效的正则化方法,以减少过度拟合并改善各种深度神经网络中的泛化误差。合理使用Dropout正则化层可以减少过度拟合并提高深度神经网络的泛化能力。
综上,Transformer-encoder模块的数据流过程可以简化表示为
(20)
(21)
(22)
Xi=Xi-1+Dropout(MutiHead(Qi,Ki,Vi))
(23)
Xi=LayerNormalization(Xi)
(24)
Xi=Conv1D(Xi)
(25)
Xi=Dropout(Xi)
(26)
Xout=Conv1D(Xi)
(27)

2.3.3 Dense层
SD网络最后一层是全连接层用于分类,使用sigmoid激活函数,表示为
(28)
输出值限制在0~1之间,通过公式(29)硬判决的方式,判定输出的值是1 b还是0 b。门限p根据sigmoid激活函数的输出范围决定,在本文中设定为0.5。
(29)
FBLNet接收机的训练以均方误差作为损失函数。公式(30)表示,通过训练学习,不断调整对权重和偏置,减小真实值与模型预测值之间的误差。
(30)
3 仿真分析
OFDM系统仿真参数如表1所示,其中发射机中的导频插入方式为梳状导频,并将发射机生成的信号数据经过瑞利衰落后全部作为神经网络的训练集和测试集。本文的信道采用服从瑞利分布的衰落信道模型,多径瑞利信道的参数使用COST207标准模型中的参数[16],该模型设定为Jakes的多普勒类型。接收端的同步技术采用基于导频的符号定时同步操作[17]。对于训练过程,使用Adam优化器,训练学习率为0.01。其中,当SNR、导频数量、循环前缀等参数变化时,根据生成的样本数据重新训练接收机模型参数。对于测试过程,本文采用与训练过程相同的参数来评价框架的误码率性能。

表1 主要仿真参数
3.1 传统接收机的对比分析
误比特率(Bit Error Ratio,BER)性能是衡量接收机解调性能影响的宏观指标。传统的OFDM接收机模型采用LS信道估计和MMSE信号检测算法组合解调算法进行仿真,称为LS-MMSE接收机。实验结果如图5和表2所示,可见在各种调制方式下,FBLTNet接收机的性能全面优于LS-MMSE方法,说明深度学习接收机更适合调制信号的解调。
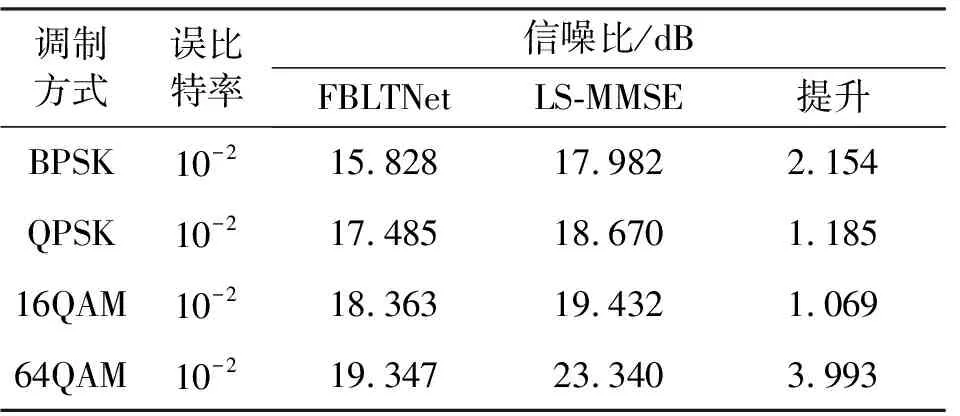
表2 瑞利信道下FBLTNet接收机和LS-MMSE接收机的信噪比对比
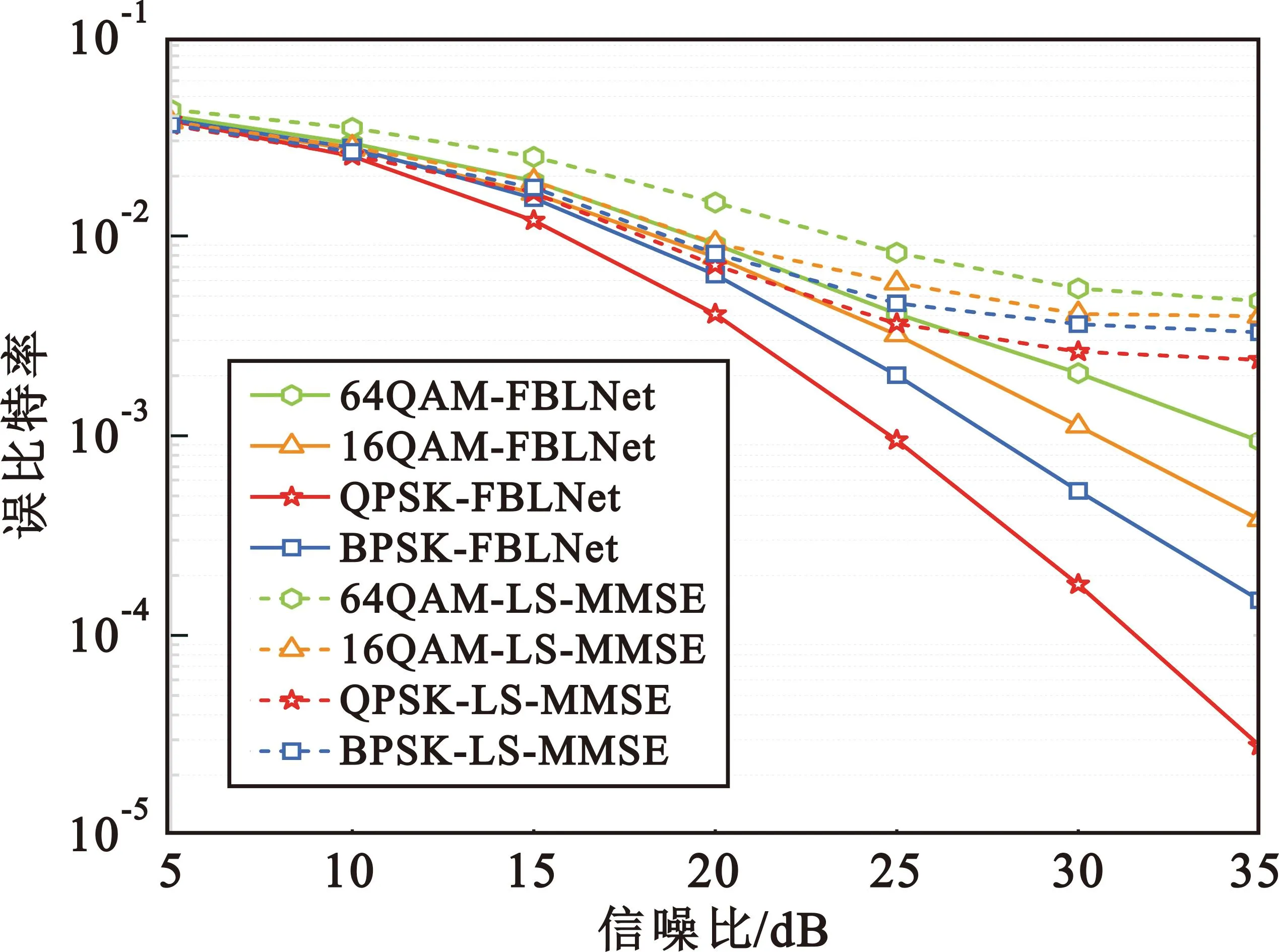
图5 FBLTNet与LS-MMSE接收机信噪比-误比特率曲线
3.2 深度学习接收机的对比分析
本文将从空间时间复杂度和误比特率两个角度,与数据驱动的FCDNN接收机[10]和模型驱动的ComNet接收机[12]进行对比分析。
3.2.1 空间和时间复杂度
神经网络的空间复杂度,主要指网络模型的参数数量。由于维度的限制,模型的参数越多即空间复杂度越高,训练模型所需的数据量就越大,不仅会导致模型的训练容易过拟合,还会增大训练的难度。时间复杂度主要取决于模型的训练和预测时间,时间复杂度过高,既无法快速地验证想法和改善模型,在实际部署中也无法做到实时解调。表3、表4和图6分别比较了FCDNN、ComNet和本文所提的FBLTNet模型的网络模型参数数量、训练时间及测试时间。

表3 空间复杂度
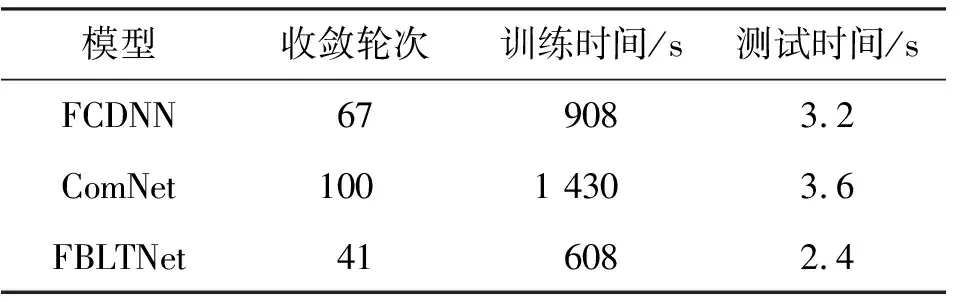
表4 时间复杂度

图6 模型训练收敛图
由表3可知,基于数据驱动的FCDNN参数量最大,远高于基于模型驱动的ComNet和FBLTNet,FBLTNet接收机与数据驱动的FCDNN接收机相比,网络结构参数减少29.5%。其主要原因是模型驱动模型每层之间除神经元之间数据传递外,在连接之间还加入了自定义的数据变换,提取更多有物理意义的信息,降低了网络结构的复杂度。
由表4可知,收敛速度、训练时间和测试时间上,FBLTNet模型最少,FCDNN次之,ComNet最多。FBLTNet接收机与FCDNN相比,线下训练模型收敛时间和测试时间分别减少33.0%和25.0%。图6表明,FBLTNet模型在训练41轮次后收敛过程开始趋于稳定,80轮次后就会出现过拟合;FCDNN在100轮次都还未出现过拟合;ComNet收敛最慢,还未达到收敛平稳状态。总之,与FCDNN和ComNet相比,FBLTNet的空间和时间复杂度均最小,这表明采用具有强大记忆能力的自注意力网络的FBLTNet,能够快速捕捉训练数据全局特征和学习数据分布特征。
3.2.2 误比特率
图7比较了FCDNN、ComNet和本文所提的FBLTNet在瑞利衰落信道的误比特率。当接收机达到特定误比特率量级时,实验结果如表5所示,可以看出,FBLTNet接收机信噪比性能与FCDNN接近,信噪比相差在0.3 dB左右。但与ComNet接收机相比,在BPSK调制方式下信噪比性能提高了1.576 dB,在QPSK调制方式下提高了4.248 dB,在16QAM调制方式下提高了1.013 dB,在64QAM调制方式下提高了0.755 dB,说明FBLTNet具有较好的信噪比性能。
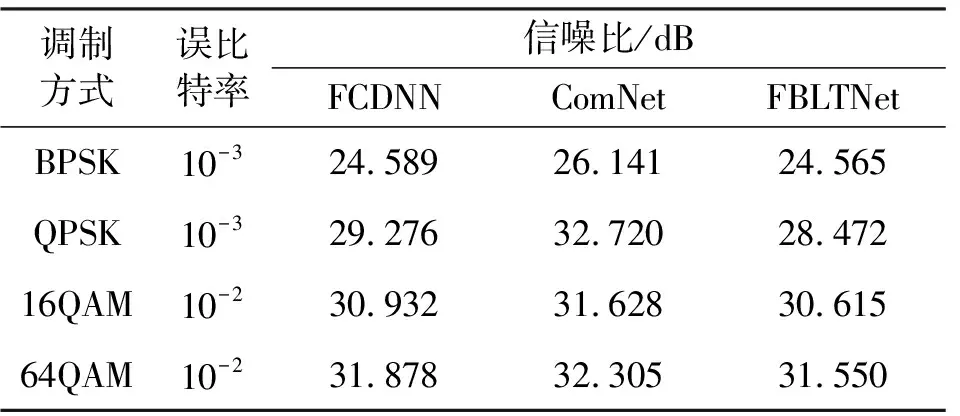
表5 信噪比性能对比

图7 多种接收机模型信噪比-误比特率对比
3.3 导频和循环前缀的影响
3.3.1 导频的影响
在OFDM通信系统中,接收端数据的同步和相干检测都需要预先知道收发天线之间的信道信息。为了获得信道的频率响应,最常用的方式是利用导频辅助信道估计算法。在传统估计算法中,适合的导频数量能够较为准确地估计出信道频率响应,但导频过多会使得频谱利用率降低。由于深度学习方法的数据拟合能力,可以采用较少的导频来估计,从而进一步提高频谱利用率。本文采用64个子载波的OFDM符号,使用梳状的导频插入方式,比较了QPSK调制方式下不同导频数量分别为4,8,16时的误比特率性能。从图8中可以看出,使用LS-MMSE算法的表现性能最差,且不同导频数量之间的误差大。当信噪比高于15 dB时,LS-MMSE接收机的误比特率曲线已经趋于饱和,而基于深度学习方法的FBLNet接收机依然具有随着信噪比的提高而降低误码率的能力。在相同量级的误比特率下,不同导频数量的接收机信噪比性能波动范围在1 dB左右。这表明FBLNet接收机对于导频数量具有鲁棒性,原因在于神经网络对于数学模型的依赖性较低,能够从模型生成的训练数据中学习无线信道的特性。
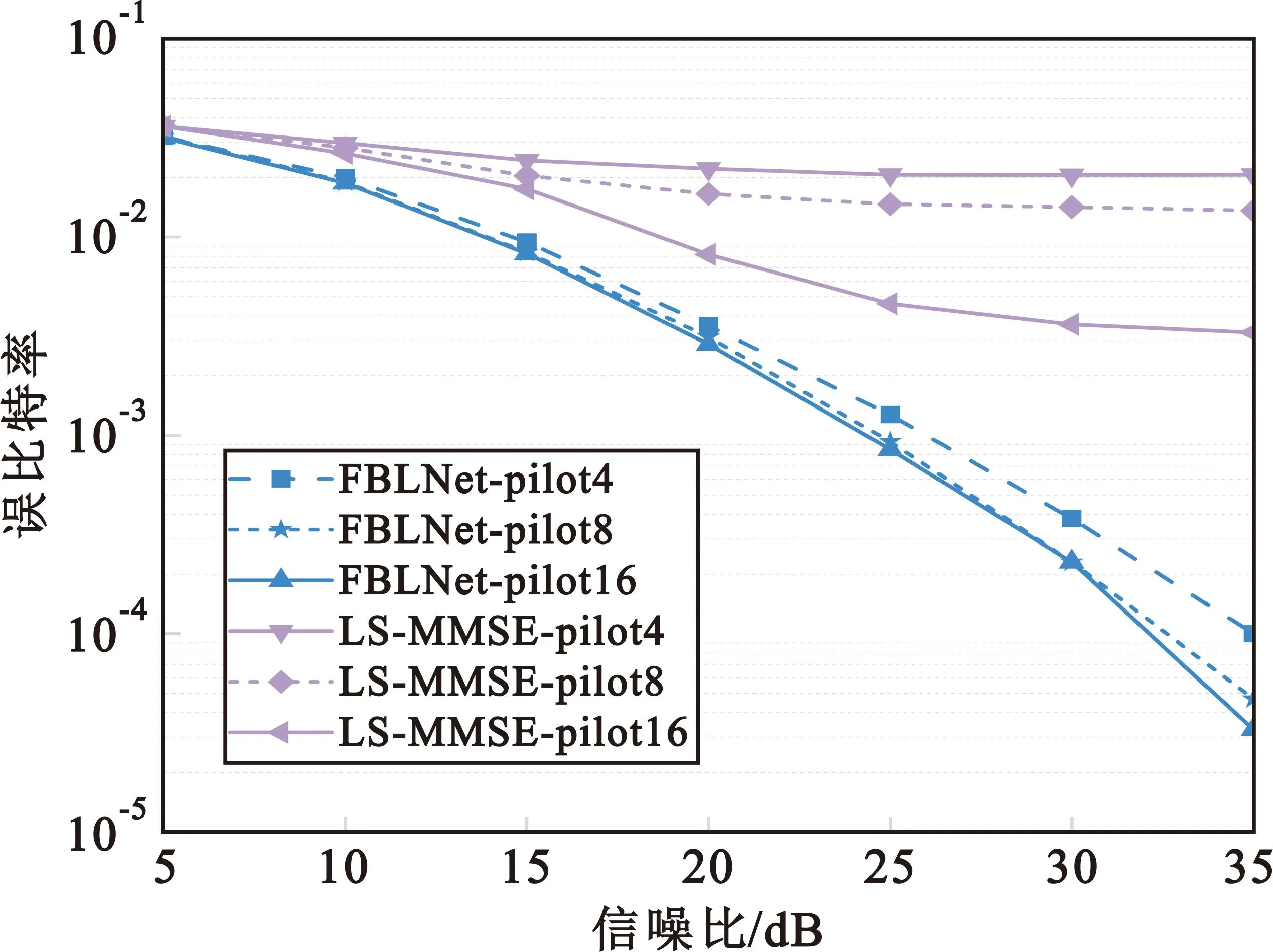
图8 导频数量对不同接收机误比特率的影响
3.3.2 循环前缀的影响
在OFDM通信系统中,传统接收机高度依赖数学模型中的循环前缀。循环前缀是将符号末尾的信号复制符号最前面,确保每个子载波之间的正交性,一次对整数时间进行FFT变换,避免信号之间的干扰,从而对抗多径衰落。但这种做法让OFDM符号长度增加,系统在移动情况下对频率误差更敏感,带来了更大的开销并降低信息的传输效率。通过舍弃循环前缀以提高频谱利用率,从图9中可以看到,在舍弃循环前缀后,LS-MMSE接收机表现敏感性最大,信噪比差异接近10 dB,而FBLNet接收机对循环前缀的使用,信噪比差异较小,最大不超过1 dB。这可解释为传统接收机方法极大依赖数学模型,舍弃循环前缀后使得子载波之间不再正交,接收端的数据对模型产生了较大的影响。反观FBLNet接收机,利用深度学习强大的数据拟合能力,且网络模型中引入了注意力机制,能够学习到符号间前后端信息的关系,说明FBLTNet接收机具有良好的抗符号间串扰的能力,也证明了在去除循环前缀的情况下深度学习方法是可行的。
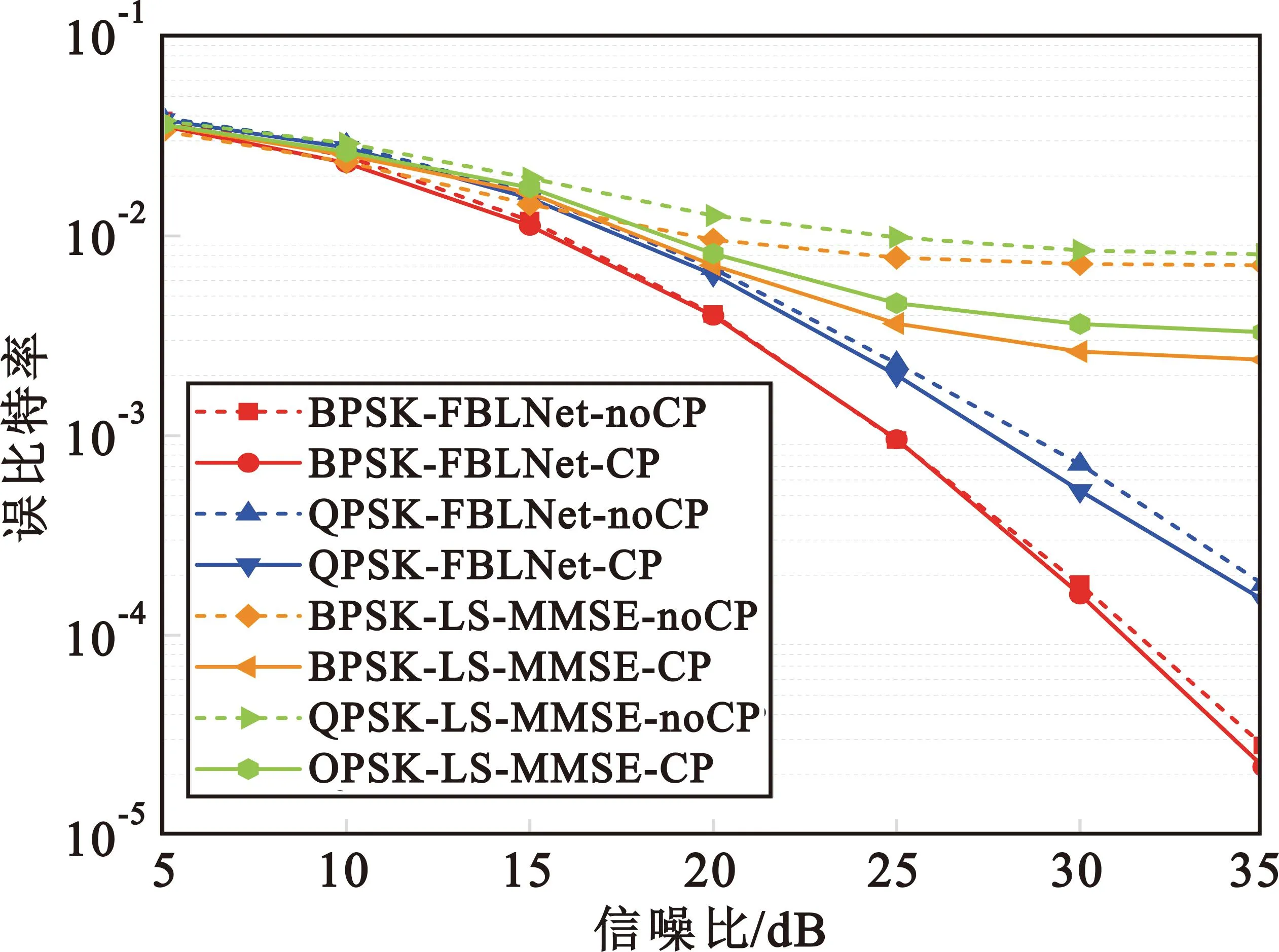
图9 循环前缀对不同接收机误比特率的影响
4 结 论
本文以OFDM无线通信系统为研究对象,采用深度学习的方法,结合神经网络和专家知识,提出了一种模型驱动接收机模型FBLTNet。测试了不同调制方式的多种接收机性能,结果表明,本文提出的FBLTNet接收机提高了模型学习符号间关系的能力,不仅能够减少模型训练的收敛时间,还加快了模型的测试时间;在瑞利信道中,与传统接收机相比,对不同的调制方式均具有鲁棒性和泛化性;与基于深度学习的数据驱动接收机相比,降低了接收机的复杂度;与基于深度学习的模型驱动接收机相比,提高了解调精度,降低了误比特率。此外通过对比分析的得出结论,导频数量的变化及循环前缀对FBLTNet接收机解调性能影响较小,在实际部署中,可以通过减少导频数量和不使用循环前缀来提高信息的传输效率。

