考虑水力耦合作用的降雨诱发土质滑坡过程数值模拟研究

曹 磊, 吴 清, 赵 广

(1.成都市城市安全与应急管理研究院,四川 成都 610023;2.四川省公路规划勘察设计研究院有限公司,四川 成都 610041;3.中国科学院地理科学与资源研究所,北京 100101)

0 引言

降雨诱发土质滑坡是我国西南山区最为普遍的灾害之一,也是灾害防治的重点[1-2]。降雨诱发土质滑坡的过程可划分为边坡失稳阶段和滑坡运动阶段,这2个阶段之间存在紧密关联。针对上述2个阶段,有研究利用室内实验[3-4]、物理模型[5-6]、数值模拟[7-8]等方法揭示其形成机理。对于土质滑坡而言,降雨入渗是坡体从非饱和状态到饱和状态的过程,该过程中坡体内部物理力学性质发生显著改变,从而导致坡体失稳破坏。以抗剪强度为例[2,5],降雨入渗导致坡体内部含水率增加与基质吸力下降,使得土体抗剪强度下降,进而造成边坡失稳。

为定量描述降雨入渗导致土体抗剪强度的改变,Lu等[9]将广义有效应力的概念引入浅层边坡稳定性计算中,并广泛应用于局部饱和条件下的边坡稳定性分析。国内外将非饱和土入渗理论引入浅层边坡稳定性研究并取得长足进展[10-11]。当边坡失稳后,如何定量描述滑坡运动过程是评价降雨诱发滑坡危害的重要前提。一方面,通过物理实验可测量直接反映滑坡运动特征的滑坡厚度和滑坡速度等[12-13]参数,随着测量技术的发展,坡体内部孔隙水压力、有效压应力以及地震动信号等参数也间接被用于分析滑坡运动特征[14-15];另一方面,数值计算方法成为滑坡运动过程定量评价常用方法之一[16-17],如Savage等[18]首次提出基于深度平均理论的滑坡物理模型,并成功应用于颗粒流、滑坡、泥石流等物质的运动模拟中[17-18];此外,侵蚀效应[19]、剪胀效应[20]等显著影响滑坡运动特征的现象也被考虑。尽管针对降雨诱发土质滑坡过程单一阶段的研究已较为深入,但有关降雨诱发土质滑坡过程多阶段的耦合研究较为缺乏,可同时模拟边坡失稳和滑坡运动过程的数值算法还有待建立。

因此,本文以降雨诱发土质滑坡过程为研究对象,建立可反映边坡失稳与滑坡运动2个阶段演化机理的物理模型,明确2个阶段转化衔接的关键因子,提出适用于2个阶段物理模型同步计算的数值方法。搭建考虑水力耦合作用下从边坡失稳到滑坡运动全过程的数值模拟流程,实现降雨诱发土质滑坡过程的定量描述,在此基础上开展数学模型的参数敏感性分析,旨在为降雨诱发土质滑坡提供一种考虑水力耦合作用的可定量化评价方法,为此类滑坡防灾减灾提供理论与技术支撑。

1 考虑水力耦合作用的降雨诱发滑坡耦合数学模型

1.1 边坡失稳数学模型

水力耦合作用对土质边坡失稳阶段的影响主要体现在降雨入渗下边坡内部土体含水率与吸应力的改变。为描述这一过程,本文采用基质势形式的Richards模型[8],模型中涉及的土—水特征曲线和非饱和渗透系数等采用Van-Genuchten公式[21]拟合。模型方程表达如下:

(1)

(2)

(3)

式中:

t—土壤吸应力变化的时间,s;

z—土壤垂向厚度,m;

ψ—土体基质吸力,Pa;

θ—土体含水率;

θr—土体残余含水率;

θs—土体饱和含水率;

C—比水容重,C=dθ/dh,其中,h表示边坡厚度,m;

Se—土体饱和度,Se=(θ-θr)/(θs-θr);

α,n,m—与边坡物理特征相关的拟合参数;

K—非饱和渗透系数;

Ks—饱和渗透系数。

考虑非饱和条件下的降雨诱发土质边坡稳定安全系数通常使用基于无限边坡假设的一维极限平衡模型进行评价[9],方程表达如下:

(4)

式中:

FoS—边坡稳定安全系数;

φ—边坡内摩擦角,°;

β—边坡斜面倾角,°;

cp—边坡内部有效黏聚力,Pa;

ρs—边坡固相密度,kg/m3;

ρf—边坡孔隙水密度,kg/m3。

1.2 滑坡运动数学模型

降雨诱发土质边坡失稳后通常处于松散及临近饱和状态,变形破坏时由于剪缩作用会产生超孔隙水压力,可降低滑坡底部有效摩擦阻力,提升滑坡流动性;相反,对于密实饱和土体,变形破坏时由于剪胀作用导致孔隙水压力消散,可增加滑坡底部有效摩擦阻力,降低滑坡流动性。因此,为考虑水力耦合作用对滑坡运动阶段的影响,本文采用可考虑剪胀效应的Iverson-George模型[20],该模型由质量守恒方程、动量守恒方程、体积含水率方程和孔隙水压力方程组成,方程表达如下:

(5)

(6)

(7)

(8)

(9)

式中:

u,v—滑坡沿x和y方向的运动速度,m/s;

gx,gy,gz—重力加速度沿x,y和z方向的分量,m/s2;

pb—滑坡内部孔隙水压力,Pa;

kap—滑坡内部侧向土压力系数,通常可设为1[17];

D—滑坡剪胀率,D=-2K(pb-ρfgzh)/μh;

μ—滑坡内部孔隙水黏度,Pa·s;

c—滑坡固相体积分数,c=1-θ;

ρ—滑坡密度,kg/m3,ρ=ρfθ+ρsc;

ω—滑坡固相压缩率;

κ—滑坡剪胀角,°,κ=atan(c-ceq),其中,ceq表示滑坡固相临界体积分数;

χ,ξ—无量纲系数,χ=(ρs+3ρf)/4ρ,ξ=3/(2ωh)+gzρf(ρ-ρf)/4ρ。

上述模型将剪胀理论耦合至滑坡运动模型,基于滑坡所处状态(固相体积分数大小)来判断其内部发生剪胀或剪缩效应,当滑坡固相体积分数大于临界值时表明滑坡处于剪胀状态,反之则处于剪缩状态,从而判定孔隙水压力消散或增加。

1.3 数学模型耦合

通过上述数学模型分析可见,含水率是同时影响边坡失稳和滑坡运动2个阶段的关键参数,可以作为实现阶段耦合的衔接因子,如图1。通过边坡失稳模型可获得边坡内部含水率、基质吸力、稳定安全系数、失稳体积等变量状态。当滑坡开始运动后,将边坡失稳体积和含水率作为初始条件代入滑坡运动模型,可获得滑坡运动过程的厚度、速度等变量状态。值得注意的是,由于Iverson-George模型是由Navier-Stokes方程基于深度平均理论简化而来,无法考虑滑坡垂直方向上的孔压分布,故滑坡物质含水率可取垂直方向上的平均值代入。

图1 考虑水力耦合作用的降雨诱发土质滑坡全过程物理模型

2 数学模型求解算法

由于上述数学模型方程的结构特征存在差异,且包含变量的演化方向也有所不同,故分别采取相应的算法进行数值求解。

针对Richards模型方程,为保持计算稳定性,采用隐式格式离散,具体离散形式如下:

(10)

式中:

k—时间迭代次数;

i—垂向计算网格位置;

ψi—非饱和区基质势在垂向i网格处取值,Pa;

Ci—比水容重在垂向i网格处取值;

Δt—单次迭代时间步长;

Δz—垂直方向网格长度。

可见,方程(10)属于典型的三对角矩阵形式,利用Tridiagonal Matrix Algorithm(TDMA)方法[22]求解。

针对Iverson-George模型方程,同样采用隐式格式离散,具体离散格式如下:

(11)

式中:

j—平面计算网格位置;

Δx—水平x方向网格长度;

Δy—水平y方向网格长度;

U—变量矩阵;

F,G—通量矩阵;

S—源项矩阵。

可见,方程(11)属于非线性双曲格式,利用Finite Volume Method(FVM)方法求解[17]。值得注意的是,为保证2个阶段模型同步计算时间的一致性,时间步长取决于2个阶段中偏小的一方。综上所述,搭建考虑水力耦合作用的降雨诱发土质滑坡过程数值流程,如图2。

图2 考虑水力耦合作用的降雨诱发土质滑坡过程数值计算流程

3 数学模型及数值算法验证

为验证所用各阶段物理模型及数值算法的适用性,首先,对杨诗秀等[23]开展的室内一维降雨入渗非饱和土壤试验进行模拟,该试验选择60cm高的砂壤土柱,分2种工况开展,一种将土柱水平放置,一端表面以饱和含水率作为进水条件(第一类边界条件),经150min后测定土柱内部含水率分布;一种将土柱垂直放置,顶端以0.02427cm/min的供水强度喷洒在土柱表面(第二类边界条件),经180 min后测定土柱内部含水率分布。土柱初始含水率θ为0.025,饱和含水率θs为0.4,残余含水率θr为0.01,渗透系数K=1.42θ10.24为土壤饱和度函数,拟合参数取值α=0.025,n=1.391。网格大小为1cm条件下的数值结果如图3中黑色虚线,表明模型数值数据与试验实测数据是一致的。

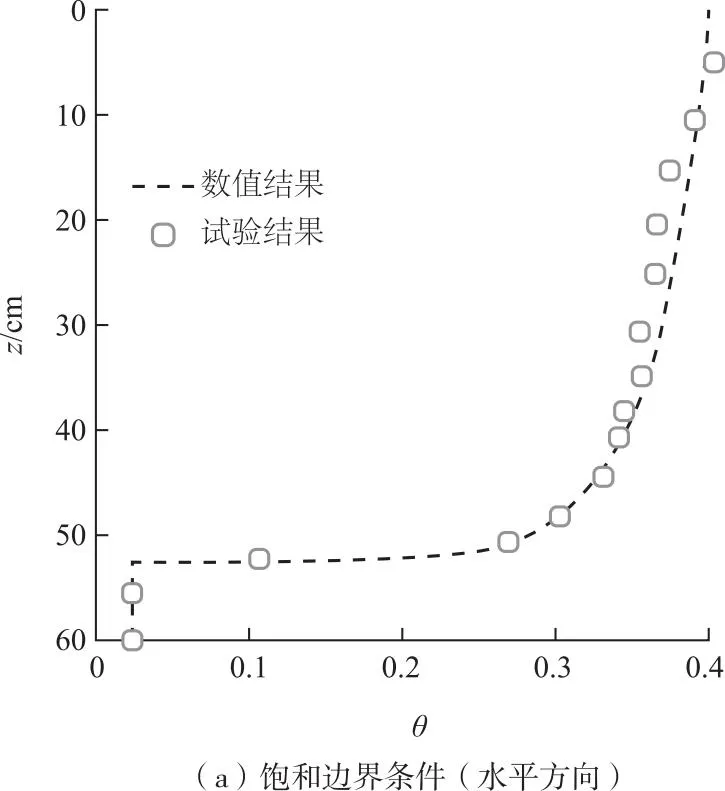
图3 2种条件下入渗监测数据与计算数据对比

其次,对2015年深圳光明新区红坳村土质滑坡运动过程开展模拟。现场调查显示,该滑坡发生时处于饱和松散状态,受剪胀效应影响具有滑动迅速、滑距长等特点[24],计算模拟参数通过相关文献资料[24-25]获取,见表1。网格大小为5m条件下的模拟结果,如图4。图4给出了滑坡运动4个时刻的厚度分布,时间为0.041667h时刻线条代表实际滑坡波及范围,滑坡堆积边缘处存在几栋被波及的建筑。结果表明计算滑坡堆积范围与实际滑坡堆积范围吻合度较好。

表1 模型计算所需参数取值

图4 深圳滑坡运动过程不同时刻滑坡形态分布

4 数学模型参数敏感性分析

为深入研究水力耦合作用在降雨诱发土质滑坡失稳及运动过程中的影响,利用上述耦合物理模型开展全过程模拟及关键参数敏感性分析。由于缺乏降雨诱发土质滑坡从边坡失稳到滑坡运动全过程的实测资料,本文采取一维数值模拟方案进行研究。具体方案设置,如图5。初始边坡位于坡度39°的斜坡上,边坡水平长5m,斜坡水平长10m,边坡初始含水率0.1,饱和含水率0.4,残余含水率0.05,饱和渗透系数7×10-9m/s,雨强50mm/h,滑坡固相临界体积分数0.64,滑面摩擦系数0.65,其余模型参数与上述模拟案例一致。

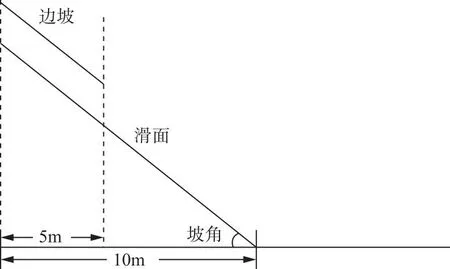
图5 降雨诱发土质滑坡初始条件示意图

边坡失稳过程计算结果,如图6。随着降雨入渗,坡体内部含水率由上到下逐渐提升,相应的坡体稳定性系数随之下降,当降雨至5h,坡面向下1m处发生失稳破坏,坡体失稳部分趋于饱和,平均含水率为0.38。将上述计算结果代入滑坡运动模型模拟滑坡运动过程(如图7),由于滑坡初始固相体积分数小于临界固相体积分数,滑坡初始滑动阶段处于剪缩状态,孔隙水压力增大,从而减少滑坡基底摩擦阻力,增加滑坡流动性,滑坡最大速度可达10m/s。当滑坡进入平面后,摩擦阻力增大,导致滑坡减速堆积,最大水平滑距为32m。

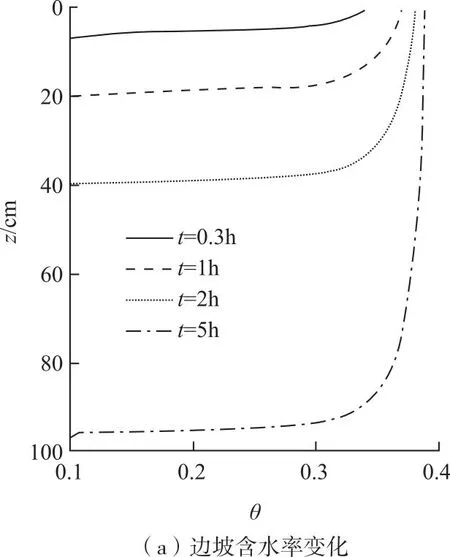
图6 降雨入渗下边坡含水率及稳定安全系数变化

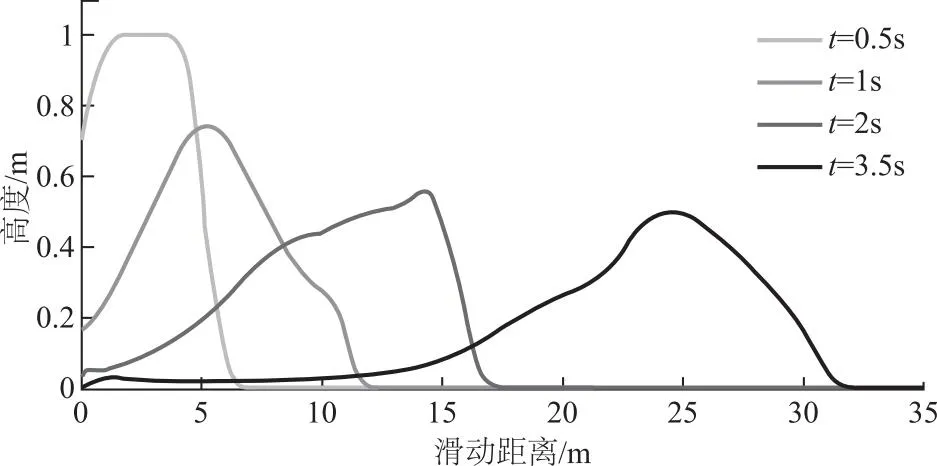
图7 滑坡运动过程中不同时刻滑坡形态

在上述案例的基础上,选择渗透系数及土体含水率作为研究水力耦合作用的关键因子开展敏感性分析。该参数对降雨入渗过程的影响分析已有较多研究成果[5-6,26],因此本文仅针对滑坡运动过程进行研究。在其余模型参数相同的条件下选取K=7×10-8,7×10-9,7×10-10进行模拟,在相同时间内的滑坡形态,如图8(a)。从图8(a)可知,渗透系数较小,水力耦合作用对滑坡运动能力影响明显,这是由于当渗透系数较大时滑坡内部孔隙水压力耗散迅速,导致滑坡底部摩擦阻力减小幅度变小,从而减少了滑坡运动距离。同样,在其余模型参数相同的条件下选取不同滑坡固相体积分数c=0.61,0.62,0.64进行模拟,在相同时间内的滑坡形态,如图8(b)。从图8(b)可知,滑坡固相体积分数小于临界体积分数时,滑坡运动能力越强,滑坡固相体积分数的细微差异可对滑坡运动能力带来显著变化。综上可知,滑坡土体物质特征(如渗透系数、含水率等)均对滑坡运动能力存在着关键影响作用。

图8 不同条件下的滑坡运动形态

5 结论

针对降雨诱发土质滑坡形成过程,将其划分为2个阶段:边坡失稳阶段和滑坡运动阶段。通过分析水力耦合作用对降雨诱发土质滑坡的影响机理,采用Ricahrds模型与Iverson-George模型相耦合,以及针对方程结构特征采用不同数值方法求解,搭建降雨诱发土质滑坡过程数值模拟流程,实现该过程的定量计算及参数敏感性分析,得到以下结论。

(1)水力耦合作用是影响降雨诱发土质滑坡过程的重要因素,且对不同阶段影响的方式存在差异。边坡失稳阶段,主要通过入渗影响边坡含水率变化;滑坡运动阶段,主要通过剪胀影响内部孔隙水压力进而改变滑坡基底摩擦阻力。

(2)通过模拟物理实验及实际案例,验证了构建的物理模型及数值算法的适用性。数值模拟分析表明,土体渗透系数及含水率均对滑坡运动能力存在显著影响。同一初始条件下,土体渗透系数越小,滑坡运动能力越强,土体趋于饱和时含水率越大,滑坡运动能力越强,相比于渗透系数而言土体含水率对滑坡运动影响程度较大。