基于循环神经网络的山前平原型城市河道洪水预报研究

陈 畅 王 帆 张大伟 向立云 芦昌兴

（1.中国水利水电科学研究院，北京 100038；2.水利部防洪抗旱减灾工程技术研究中心（水旱灾害防御中心），北京 100038；3.水发规划设计有限公司，济南 250000）

0 引 言

在气候变化和城市化快速扩张的背景下，我国城市洪涝问题日益凸显[1]，如济南市2007 年“7·18”特大暴雨、北京市2012 年“7·21”特大暴雨、西安市2016 年“7·24”暴雨和郑州市2021年“7·20”特大暴雨，均造成了严重的洪涝灾害[2]。城市化建设改变了流域自然面貌和排水格局，增加了不透水面积，侵占了河湖水系，对流域的自然水循环过程产生了极大的影响[3]。城市化的水文效应主要表现在：①硬化的地表取代了原有的裸露土壤和植被覆盖，削弱了地表截留、蒸散发和下渗能力，改变了自然的产流特性[4]；②城市路面、地下排水管网和下凹式立交桥、涵洞等构筑物的建设，改变了原有的坡面和地下汇流特性[5-6]；③渠化的河道及水闸、橡胶坝、堰等水工建筑物的建设，改变了原有的河道汇流特性[7]；④城区内大量的混凝土建筑的高热量排放，引起了局地小气候的改变，产生“热岛”“雨岛”效应，增加了极端暴雨发生的频率[8]。

相较于自然流域，城市的产汇流过程更为复杂，尤其是城市管网、河道和地表洪水演进等水流运动过程具有明显的水动力学特征，面向自然流域的传统水文模型难以满足城市水文模拟和洪水预报的需求[9-10]。针对我国平原型城市，徐向阳[11]构建了包含产流、坡面汇流、管网汇流和河网汇流4个子模型的城市雨洪模型。刘家宏等[12]基于下垫面条件将城市区域划分为不透水单元、透水单元和半透水单元等6类基本单元，并通过城市管网和河湖水系将各单元连接至城市水文模型系统，弥补了城市洪涝模拟在水文学机理方面的不足。在城市洪涝模拟软件方面，自20世纪70年后，形成了一系列较为成熟的产品，包括国外的SWMM、Info-Works ICM、STORM 和IUHM 等[8]，以及我国的GAST[13]、HydroInfo[14]、FASFLOOD[15-16]和IFMS/Urban[17]等，为城市洪涝模拟与预报提供了有力支撑。朱呈浩等[18]基于SWMM 构建了西安沣西新城区洪涝模型，计算了该区域在不同重现期暴雨中的洪涝过程。曾鹏等[19]基于IFMS/Urban 构建了成都市中心城区内涝模型，实现了对不同设计降雨下的城区暴雨内涝特征的分析。此外，还有很多新技术新方法也被应用于城市洪涝模拟。潘鑫鑫等[20]建立了耦合物理过程模型和机器学习算法的模拟，规避了复杂方程组求解问题，实现了对城市调蓄池控制节点水位的高速高效高精度预测。韩浩等[21]提出了一种基于多GPU并行的新型流域雨洪过程模拟方法，实现了大尺度流域雨洪过程的高性能模拟。

近年来，循环神经网络凭借其优异的性能在洪水预报领域受到了广泛的关注[22]，在城市河道洪水预报方面也有了一定的应用研究。Gude 等[23]基于长短期记忆网络（Long Short-Term Memory，LSTM）构建了美国密苏里州Meramec河St.Louis 区的水位预测模型。Ahmed 等[24]利用基于Boruta 算法的随机森林模型（Boruta-Random Forest，BRF）对输入变量进行特征提取，然后结合LSTM 和门控循环单元（Gated Recurrent Unit，GRU）网络构建了中长期预测模型，利用该方法在澳大利亚Murray Darling 流域进行了月尺度的水位预测。Liu 等[25]基于LSTM 网络构建了福建福州市城市内河和外河水位的实时滚动预报模型。LSTM 和GRU 等具有门控机制的循环神经网络，对于处理水文序列中的长期依赖问题（long-term dependencies problem）非常有效，成为流域和城市洪水预报的新方法，但在山前平原型城市河道洪水预报方面尚未进行深入研究。

山前平原型城市拥有特殊的浅碟状地势，发生强降雨时山洪快速下泄至城区，容易进一步加重城区的洪涝灾害[5，26]，其洪水兼具了山洪和城市洪水的特征，因此对水文模拟和洪水预报模型提出了更高的要求。胡伟贤[27]基于SWMM 构建了济南市城市雨洪模型，并利用实测雨洪数据验证了模型的可靠性和适用性。常晓栋等[26]进一步将山前平原型城市的子汇水区分为山区、平原区和主城区3类，并指出根据不同地形特点设置相应的汇流演算方式、模型演算面积比及河段糙率系数能够显著提高模拟精度。程涛等[28]利用InfoWorks ICM 构建了济南市山前平原区的一维排水管网模型和二维地面淹没模型，并对研究区内节点溢流和地面淹没情况进行定量模拟，并验证了模型的适用性。

本文拟采用目前在流域洪水预报领域应用较为广泛的循环神经网络，以小清河济南市黄台桥水文站以上流域为研究对象，构建山前平原型城市河道洪水预报模型，并探索其对具有复杂下垫面条件流域洪水预报的适用性，以期为山前平原型城市河道洪水预报预警提供参考。

1 模型方法与评价指标

1.1 模型方法

Hochreiter 和Schmidhuber[29]在循环神经网络中创新性地引入了门控机制，构建了LSTM 网络，有效地解决了序列预测中“长期依赖信息”学习的问题，其单元内部结构见图1（a），其中包含遗忘门z(t)f、输入门z(t)i和输出门z(t)o3 个门结构，用于控制信息传递。Chung 等[30]在LSTM 的基础上提出了GRU 网络，将门结构简化为更新门z(t)u和重置门z(t)r，其内部结构见图1（b）。相比于LSTM，GRU 的结构更简单、参数更少、训练效率更高，研究表明其在保持与LSTM 相近的模拟精度的前提下，具备更快速的收敛能力[31-32]。

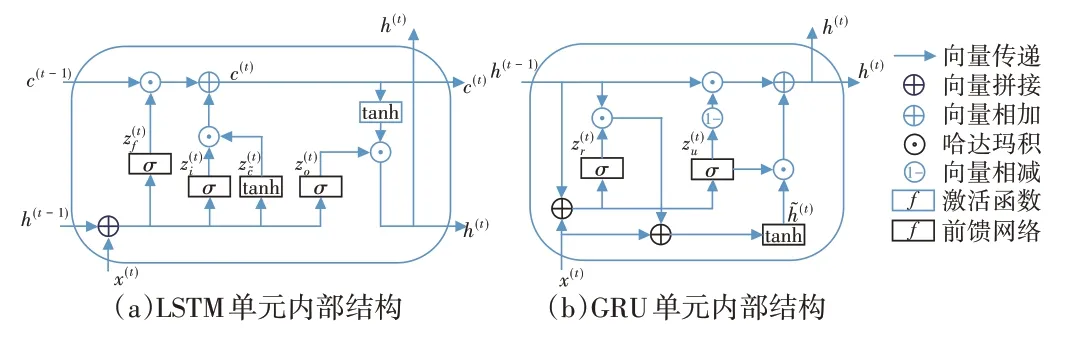
图1 LSTM与GRU单元内部结构

为更全面地利用时间序列中的信息，Schuster 和Paliwal[33]提出了双向循环神经网络（Bidirectional Recurrent Neural Networks，BiRNN）结构（图2），由此也衍生出了双向长短期记忆（Bidirectional Long Short-Term Memory，BiLSTM）[34]和双向门控循环单元（Bidirectional Gate Recurrent Unit，BiGRU）[35]等网络，他们可以同时在正向和反向上进行训练，从而能够从时间序列数据中提取历史和未来方向的特征，提升预测性能[36]。本文尝试基于LSTM、GRU、BiLSTM 和BiGRU 网络构建洪水预报模型，并进行性能对比，探索其对山前平原区城市河道洪水预报的适用性。

图2 双向循环神经网络结构图

1.2 评价指标

本文从洪峰流量、峰现时间和整体过程3 个角度对流量过程的预报精度进行评价，选择洪峰相对误差（δRPE）、峰现时间误差（ΔPTE）和纳什效率系数（NSE）作为评价指标[37]。

洪水预报的首要任务是对洪峰流量的预测，特别是对于中小河流[38]。通常洪水起涨和消落较快，对洪水起涨阶段或洪峰流量的准确预测通常意味着整体过程预报精度较高，因此本文选用洪峰相对误差作为评价指标，如式（1）所示：

式中：Q为模拟序列的洪峰值，m3/s；Qobsmax为实测序列的洪峰值，m3/s。

峰现时间误差计算方式如式（2）所示：

式中：T为模拟序列的峰现时间，h；T为实测序列的峰现时间，h。

纳什效率系数计算方式如式（3）所示，其描述了模拟序列与实测序列之间整体偏差的大小。NSE越接近1，表示模拟精度越高，若小于0，则表示模型结果劣于实测值均值序列。

式中：Q、Q分别为实测和模拟序列t时刻的流量，m3/s；为实测流量序列的均值，m3/s；M为实测序列的长度。

本文还选取了均方根误差（Root Mean Square Error，RMSE）、平均绝对误差（Mean Absolute Error，MAE）及最大水位误差（ME）作为评价指标，具体计算公式如下：

式中：Z和Z分别为t时刻流量的模拟值与实测值，m3/s。N为场次洪水总数。

2 研究区域和数据资料

2.1 研究区域

小清河流域发源于济南市西部睦里庄，自西向东流经济南市、淄博市、滨州市、东营市、潍坊市，于寿光市羊角沟入海，全长237 km，控制流域面积10 336 km2，是济南市重要防洪除涝河道，也是主城区唯一排水出口。流域多年平均降水量为619.7 mm，降水年际变化较大，年内分配不均。

本文选取小清河黄台桥水文站以上流域为研究对象，黄台桥水文站位于济南市历城区[39]，东经117°04′、北纬36°44′，控制流域面积321 km2，上游有刘家庄、吴家铺、东红庙、兴隆、燕子山共5 座雨量站，研究区域位置及站点分布见图3。

图3 研究区域位置及站点分布图

2.2 水文资料

本文收集了黄台桥水文站及其流域内5 座雨量站1998年、2004年、2007年、2009年、2011年、2013年、2015年、2016 年、2018 年、2019 年、2021 年的实测降雨、流量和水位数据。基于收集的水文数据进行了场次雨洪过程提取，筛除其中雨洪不对应的场次，最终得到41 场洪水过程，其中涵盖了单峰、双峰和多峰型洪水过程，具有较好的代表性。

3 预报模型构建

3.1 数据归一化处理

由于降雨、流量和水位数据存在量纲和尺度差异，会对模型精度及收敛速度造成影响，因此首先采用线性归一化方法进行预处理，计算公式如式（7）所示：

式中：xnorm为归一化数值；x为观测值；xmax和xmin分别为观测值的最大值、最小值。

3.2 输入输出设置

本文分别以流量、水位作为输出变量构建预测模型，考虑到降雨、流量和水位序列之间的相关性，在输入变量选择方面设置了多种组合方式，如表1所示。在输入、输出步长选择方面，参考王帆等[37]的工作，通过试算得到不同输入组合条件下的评价指标分布（图4、图5），最终确定模型的输入时段长为6 h、输出时段长为3 h，预测流量过程的输入变量为降雨、流量，预测水位过程的输入变量为降雨、水位。

表1 输入输出变量设置

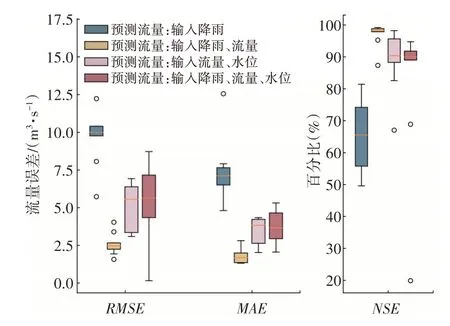
图4 不同输入组合预测流量的评价指标

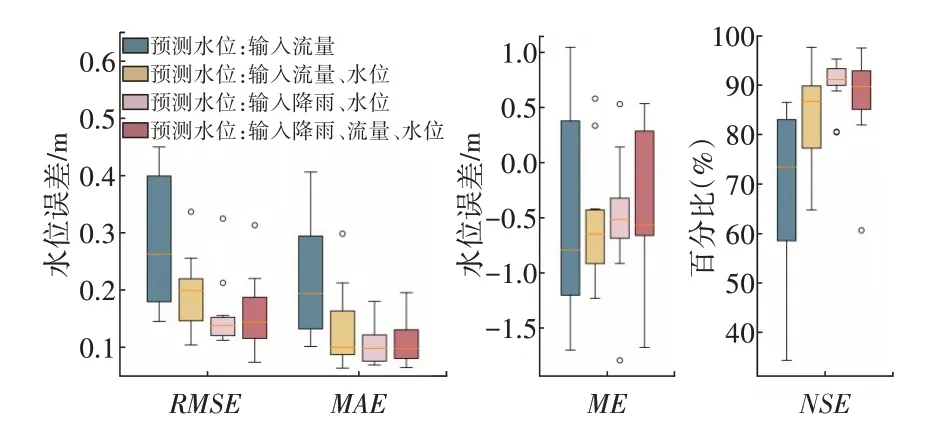
图5 不同输入组合预测水位的评价指标

3.3 数据集划分

对归一化处理后的场次降雨洪水数据进行划分，从所有洪水场次中不放回地抽取11场洪水作为测试集场次，将余下的场次按照输入输出步长进行切片，生成训练样本，从中随机选取10%作为验证集样本，其余样本作为训练集样本，各集合洪水场次及样本个数见表2。

表2 洪水场次及样本个数

3.4 模型超参数设置

通过调整模型的超参数，使模型训练集和验证集损失函数均达到较优状态，其中神经元个数与批大小均以2 的次幂进行试算，最终确定模型超参数如表3所示。

表3 模型超参数设置

4 模拟结果分析

利用基于BiGRU 网络构建的洪水预报模型，对测试集场次洪水进行了模拟预报，流量和水位过程的预报结果评价指标分布如图6、图7 所示。由图6 可见，当预测步长在2 h 以内时，模型对洪峰流量、峰现时间和洪水过程均有着较高的预测精度。当步长为3 h时，预测散点逐渐偏离1∶1理想线，模型的预测性能有所下降，对洪水过程的预测误差明显增大，但洪峰相对误差依然维持在较低的水平。由图7 可见，模型对低水位过程的预测精度较高，接近于1∶1 理想线，对于高水位的预测整体偏低。随着预测步长的增加，模型同样呈现出性能下降的趋势。

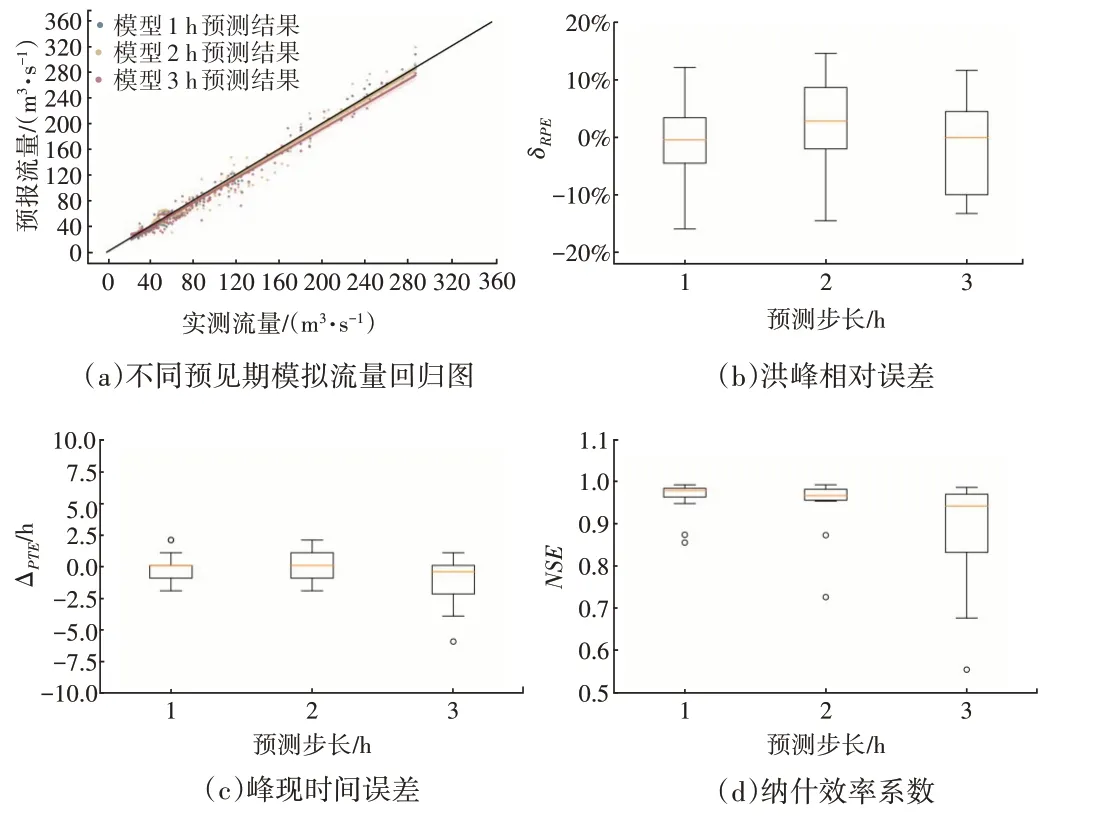
图6 BiGRU模型预测流量的评价指标

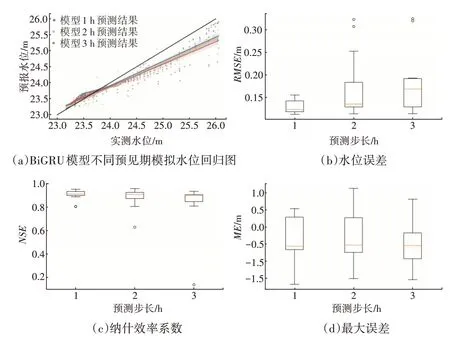
图7 BiGRU模型预测水位的评价指标

表4 和表5 显示了4 种不同模型在预测流量和水位时的预报准确性评价指标。由表4 可以看出，在预测流量时，预报精度随着预见期的增加而逐渐下降。双向神经网络BiLSTM 与BiGRU 模型的RMSE、MAE和NSE指标分别为15.70—17.58、12.27—13.20、0.768—0.898与15.29—16.75、11.39—12.14、0.874—0.965，预报精度明显比单向的循环神经网络LSTM 与GRU 模型高。随着时间推移，BiGRU 模型在预测流量时表现得更好。

表4 循环神经网络的预测精度评价指标（流量）

表5 循环神经网络的预测精度评价指标（水位）

由表5可以看出，在预测水位时，预报精度同样随着预见期的增加而下降。BiGRU网络的RMSE、MAE和NSE指标分别为0.48—0.50、0.32—0.34、0.796—0.851，表现比其他循环神经网络预测效果要好。整体比较流量和水位的NSE，可以看出流量过程的预测精度要高于对水位过程的预测精度。

本文从测试集洪水场次中选取“2018.8.13”“1998.8.2”两场洪水过程，对比分析LSTM、GRU、BiLSTM 和BiGRU 模型的预测性能。“2018.8.13”场次洪水预报流量过程如图8所示，可见各模型均能准确地预测洪水的涨落过程，在对洪峰流量的预测方面，基于BiLSTM 和BiGRU 的模型要明显优于基于LSTM 和GRU 网络所构建的模型。“1998.8.2”场次洪水包含3 次连续的洪峰和退水过程，模型的连续模拟预测时间超过300 h，由图9 可见，模型对洪水过程的整体趋势能够进行准确的预测，适用于洪水过程的连续模拟。在模型性能方面，基于LSTM 和GRU 网络所构建的模型表现出相近的性能，而基于BiLSTM 和BiGRU 网络所构建的预测模型性能明显更优，证明了双向网络能够更好地提取降雨、流量序列特征。

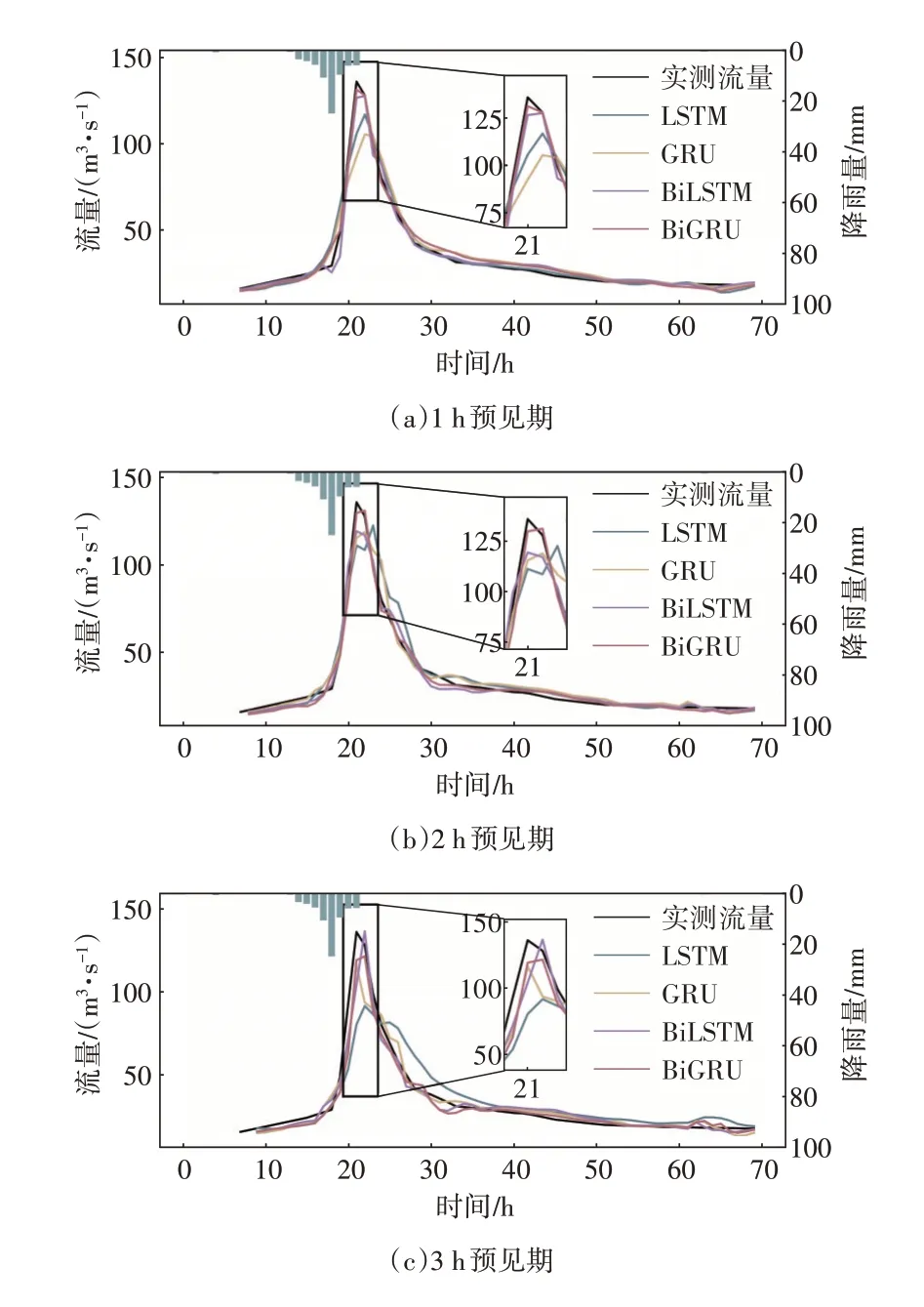
图8“2018.8.13”场次洪水预报流量过程

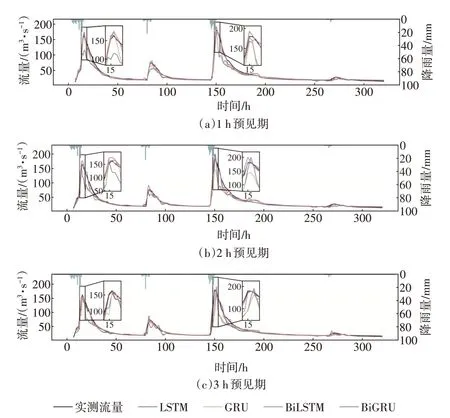
图9 “1998.8.2”场次洪水预报流量过程

相比于对流量过程的预测，各模型的水位预测精度均略有下降，如图10、图11 所示，预测水位过程存在明显的锯齿状波动，其中基于LSTM 和GRU 网络所构建的模型尤为明显。基于BiLSTM 和BiGRU 网络所构建的模型预测精度相对较高，尤其是基于BiGRU 的模型，随预测步长的延长，预测性能几乎没有衰减。

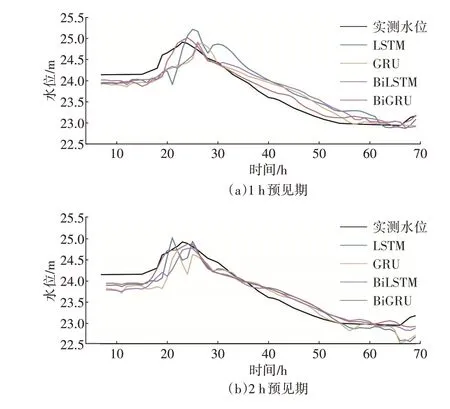
图10 “2018.8.13”场次洪水预报水位过程

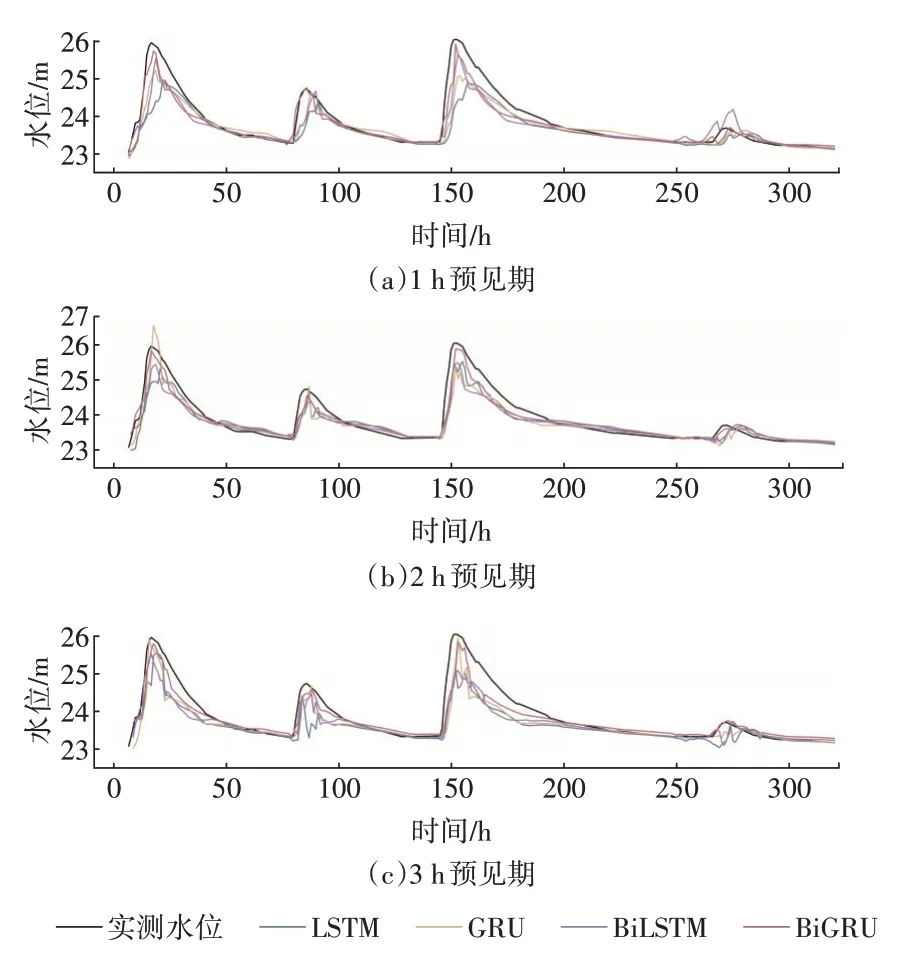
图11 “1998.8.2”场次洪水预报水位过程

5 结 论

本文针对山前平原型城市河流，开展了基于循环神经网络的洪水预报模型构建工作，以小清河济南市黄台桥水文站以上流域为研究对象，评估了BiGRU 等循环神经网络变体的适用性，主要得到以下结论。

（1）基于LSTM、GRU、BiLSTM 和BiGRU 网络所构建的洪水预报模型均能够准确预测洪水的涨落过程，虽然预测性能随预测步长的延长有所衰减，但在较短步长内拥有较高的预测精度，证明了其对具有复杂下垫面特征的山前平原型城市河流洪水预报的适用性。

（2）相比于传统水文模型，以神经网络模型为代表的数据驱动模型，能够通过建立映射，灵活地设置输入、输出变量，本文的研究表明降雨是模型的必要输入，而通过增加流量、水位等输入能够进一步提高预测精度。

（3）基于循环神经网络所构建的模型，既适用于对场次洪水的预报，也适用于对长系列过程的连续预测，整体看来，其对流量过程的预测精度要高于对水位过程的预测精度，且对低水位过程的预测精度要高于对洪峰水位的预测精度。

（4）在本文尝试的4种循环神经网络变体中，基于BiGRU 网络所构建的模型预测性能最优，一方面在于其对洪峰、峰现时间及洪水过程的模拟精度更高，另一方面在于随预测步长的延长，其预测性能衰减最弱。