考虑时间效应的VMD-BiLSTM径流量预测模型研究

严春华，侯钧宇，梅 杰，蒋肇冰，姜中清，徐乔婷

（1.江苏省水利勘测设计研究院有限公司，江苏扬州 225100；2.淮安市水利工程建设管理服务中心，江苏淮安 223001）

1 概 述

流域中河流、水库、湖泊径流量的预测对流域的性态掌握和安全判断十分重要。目前，基于智能算法对径流量的预测［1-2］研究成果很多，如左亚会等［3］基于改进RBF网络模型实现了对流域水文的中长期预测；张上要等［4］借助TCN 算法构建径流量预测模型，实现对渭河流域月径流量的预测；唐铭泽等［5］通过ASWPD-BO-GRU 3 个算法建立了月径流量预测模型，其预测模型的精度满足工程的需要；严春华等［6］结合偏自相关分析方法和残差修正方法提出了径流量GRU 的预测模型。基于智能算法能够对径流量进行较好的预测且精度较高，但径流量作为非稳态的复杂变量，各河流不同断面的径流量具有时变性和互异性，需要进一步分析径流量所包含的特性，从而构建合理的预测模型，以提高径流量的预测精度。

直接学习预测径流量，容易受到径流量中噪声残差的影响，导致预测精度较难提高。为解决该问题，需对径流量进行分量分解。（1）本文采用（variational mode decomposition，VMD）算法对径流量进行分解，以更全面反映径流量所包含的特征信息。该算法已大量应用到水利工程中的信号分解，得到了工程实际验证。陈天涯等［7］通过VMD 算法对水电机组振动信号进行分解，从而提高了水电机组振动预测的精度；张建中等［8］借助VMD对大坝变形测值进行分解，构建了基于优化VMD 与GRU 的混凝土坝变形预测模型，提高了大坝变形预测模型的预测水平。径流量除了包含不同特征外，还具有一定的时间效应，即前后径流量有时间尺度上的关联性，需要刻画这种关联性，以提高径流量的预测精度。（2）本文采用BiLSTM 深度学习算法对时间效应进行捕捉，同时得到径流量各分量的映射网络。该算法通过正向和反向双向学习训练，能够得到变量前后间的关系，该算法已经在电力、土木、水利等多个行业领域应用。习伟等［9］采用BiLSTM 算法并融合多元影响因素对配电台区负荷进行了预测；杜睿山等［10］基于CNN-BiLSTM-AM提出了储层岩石脆性指数预测模型；刘可真等［11］基于BiLSTM构建了小水电日发电量预测模型，并较大幅度地提高了预测精度。虽然BiLSTM 深度学习算法的学习能力强，但该算法具有复杂的网络结构，导致该算法为达到全局最优容易出现局部过拟合的现象，同时复杂的网络结构还会降低算法的学习效率。因此，采用Dropout 技术对BiLSTM 的网络进行优化，以提高其学习精度和效率。

综上，本文采用VMD算法对径流量进行变量分解，得到IMF 系列分量，并采用Dropout 技术对BiLSTM进行优化，然后对径流量各个IMF分量进行训练学习，得到各个IMF 分量的映射网络，将各个IMF 分量的预测值相加即为径流量的预测值，从而构建基于VMD-BiLSTM 径流量预测模型。为了验证该模型的精度，计算研究对比模型的径流量预测值及精度，其中对比模型包括VMD-LSTM 模型、BiLSTM和LSTM模型。

2 模型基本理论及实现框架方法

2.1 VMD算法基本理论

径流量具有较高的非稳态特性，是非稳态信号的一种。对于非稳态的信号分解，经验模态分解（empirical mode decomposition，EMD）是常用的方法。但对于非线性程度高的变量，借助EMD分解容易存在模态混叠，其表现为包含不同信息特征的分量掺杂在一起，揭示分量信息的不全面。为解决该问题，集合经验模态分解（ensemble empirical mode decomposition，EEMD）对EMD 进行了优化处理，但该分解方法由于加入白噪声而较为严重地影响了分解速度，噪声处理也存在一定的难题。2014年有研究提出VMD 算法以从根本上解决EMD 和EEMD所存在的问题。与EMD 系列的自适应方法最大的区别是，VMD借助迭代来确定每个模态函数和对应的中心频率和带宽，并把信号的局部特征进行放大处理，得到了更加精确稳定的各分解分量的信息。

VMD 通过建立求解变分问题来完成原始信号的分解。VMD 算法通常采用交替乘子算法进行变分问题的解答。VMD分解的基本思路为首先采用交替乘子算法更新IMF 分量中心频率，然后借助傅里叶逆变换得到IMF 分量在时域上的表示，最后求得原始信号的IMF系列分量。变分问题的求解对信号特征要求较高，可以把信号转换为扩展的Lagrange，再借助交替乘子算法以交替更新模态函数uk、ωk中心频率和拉格朗日算子λ的方式完成对变分问题的解答。由此可知，VMD算法的实现流程为：

第一步：对uk、ωk、λ进行初始化处理，并确定循环次数n。

第二步：循环计算n=n+1。

第三步：通过VMD 迭代计算uk和ωk，其中只迭代频域ω＞0的部分。

第四步：计算拉格朗日算子λ。

第五步：循环步骤2 至步骤4，直到满足设置精度要求或者停止条件，从而得到K个unk+1。

第六步：通过反傅里叶变换对K个unk+1进行变换，计算实部部分，可以得到最后的K个模态分量的时域表示uk(t)。

2.2 BiLSTM深度学习算法

由于径流量具有时间效应，而单向的LSTM 模型较难捕捉前后时间尺度上的信息，因此，通过2个方向的LSTM 网络学习，可实现预测模型对径流量双向信息的捕捉。而为了LSTM 可以实现对特征2个方向的学习，构建了双向学习的LSTM算法，即为BiLSTM模型。

由于BiLSTM模型是由LSTM网络拼接而成，首先需要了解LSTM 网络结构。LSTM 网络结构是RNN 的一种，其学习的反馈机制一致，再引入记忆单元（memory cell）和门（gate）机制，实现对历史信息的传递和丢弃处理。而且记忆单元具有独特的门控机制，解决了梯度下降中的衰减问题，有效避免了网络学习中的梯度消失现象。LSTM通过输入门（input gate）、遗忘门（forget gate）和输出门（output gate）来完成对训练学习中的信息处理。如果有新的神经单元输入，遗忘门和记忆单元相乘丢弃记忆单元中的无效信息；紧接着输入门则把当前时刻的有效输入矩阵和当前的计算状态更新到记忆单元；最终输出门把当前记忆单元的值输出，同时更新隐藏层的信息，用于下一个神经网络层的输入。LSTM内部神经元表达式见式（1）到式（6）。

（1）遗忘门输出值ft的表达式为

（2）输入门输出值it的表达式为

（3）内部记忆单元输入值c%t的表达式为

（4）内部记忆单元ct的表达式为

（5）输出门输出值ot的表达式为

（6）隐藏层输出值ht的表达式为

式中：xt为t时刻输入层的输入向量；ht为隐藏层的输出向量；ot为输出层的输出向量；W和b分别为各自门所对应的权重矩阵和偏置量。

BiLSTM 模型是通过拼接一个向前一个向后的LSTM 神经网络，从而得到径流量时序的每个点的上下时刻的相互影响的信息。BiLSTM 网络结构如图1所示。

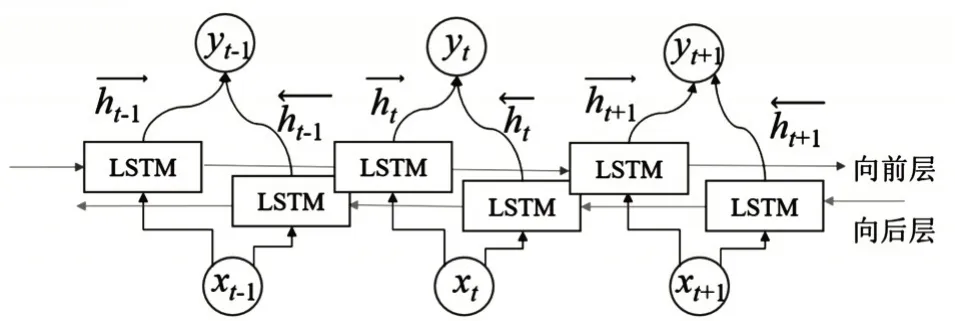
图1 BiLSTM网络结构

BiLSTM 与LSTM 相似，一般采用BPTT 算法对梯度进行求解，并解决了算法在学习过程中信息发散和梯度爆炸的难题，从而最大效率地学习到间隔比较远的信息。由于BiLSTM 较之LSTM 的结构复杂，存在计算速度慢和学习时间长的问题，需要对BiLSTM 的学习网络进行优化以进一步提高算法的效率和精度。其中BiLSTM 深度学习算法常存在的问题就是非线性训练的过拟合，因此在对其网络优化的过程中需要重点解决该问题。Dropout 技术的最大优势在于可以处理学习过程中的过拟合问题。为了解决BiLSTM 深度学习所存在的问题，采用Dropout 技术对其网络结构进行优化。当学习网络的参数较多而提高的数据集较少时，容易存在过度学习训练的情况，即仅仅保证训练集的精度高而验证集的精度却相对较低，无法满足预测的需要，所以需要对学习网络进行正则化处理，尽可能地避免过拟合现象，减少学习网络的失误程度，提高模型的学习能力。Dropout 技术从优化网络结构出发而不是采用代价函数来解决过拟合的问题。Dropout的核心逻辑为通过BiLSTM算法在学习的过程中停止一定数量的神经元并保证该次学习的权重不变，来提高算法的拟合效率和拟合精度。Dropout技术的逻辑框架如图2所示。

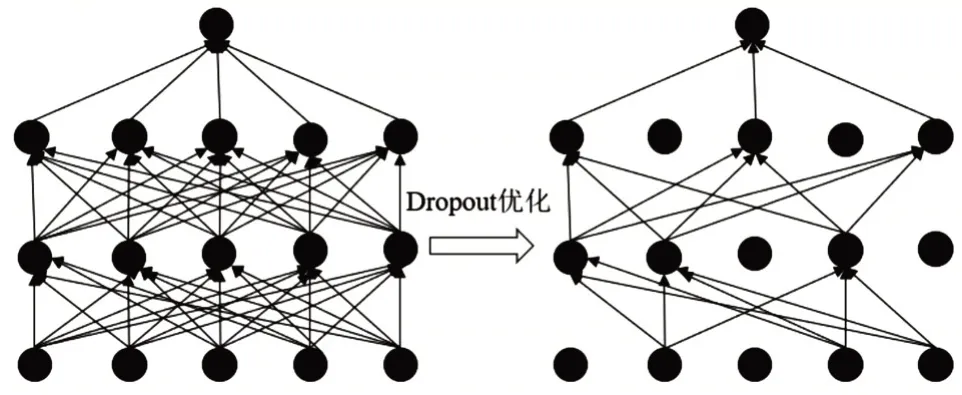
图2 Dropout优化逻辑框架

2.3 径流量预测模型的构建及实现流程

本文通过VMD算法和BiLSTM深度学习算法联合构建径流量预测模型，详细流程如下：

第一步：收集研究流域对象的径流量资料，以及流域的降水和水位等水文资料。

第二步：确定所研究流域的数据集，划分数据集的训练阶段和预测阶段，数据集包括训练集和预测集。

第三步：采用VMD 算法对径流量进行分解，得到最优的分解IMF分量。

第四步：通过BiLSTM 算法对径流量的各IMF分量进行训练，其中降水和水位是输入量，IMF分量为输出量。

第五步：得到输入集和IMF分量的映射网络，将各IMF分量相加即为径流量的拟合值。

第六步：把预测集中的输入变量代到训练好的各IMF分量的映射网络，得到各IMF分量的预测值。

第七步：将各径流量IMF 分量的预测值相加得到径流量的预测值。

第八步：计算对比模型的径流量预测值，对比模型包括VMD-LSTM模型、BiLSTM和LSTM模型。

第九步：分析各径流量预测模型的精度和误差。

综上可知，基于VMD-BiLSTM的径流量预测模型实现流程如图3所示。

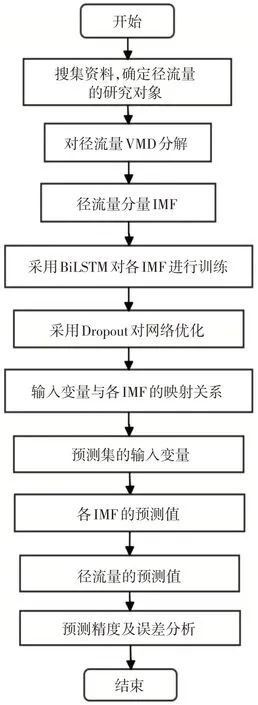
图3 基于VMD-BiLSTM的径流量预测模型实现框架

3 工程案例

3.1 工程概况

长江一级某支流，干流全长423 km，流域面积1.67万km2。径流量的监测断面位于湖北省巴东县，该断面的径流量过程线如图4所示。径流量的数据集时间从2015 年1 月1 日到2017 年7 月1 日，监测频次为一天一次，其中训练阶段从2015 年1 月1 日到2017年2月28日，预测阶段从2017年3月1日到2017年7月1日（图中框中标出）。与径流量具有较高相关性的降水和水位作为预测模型的输入，两者的具体变化情况分别如图5和图6所示。

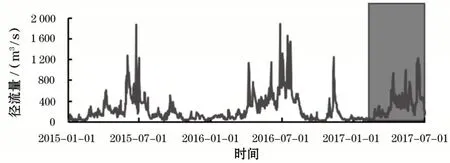
图4 断面的径流量

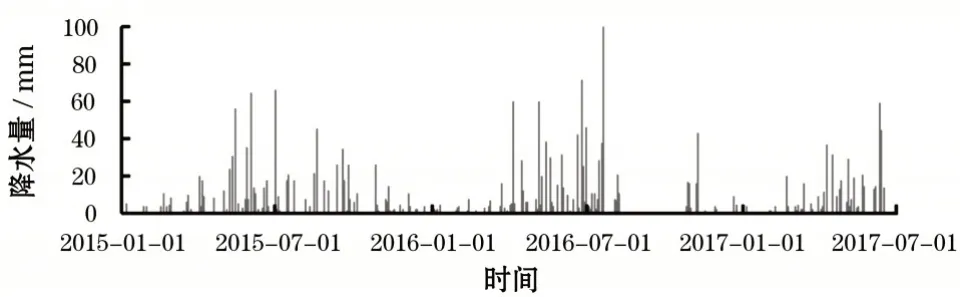
图5 断面的控制流域内的平均降水量

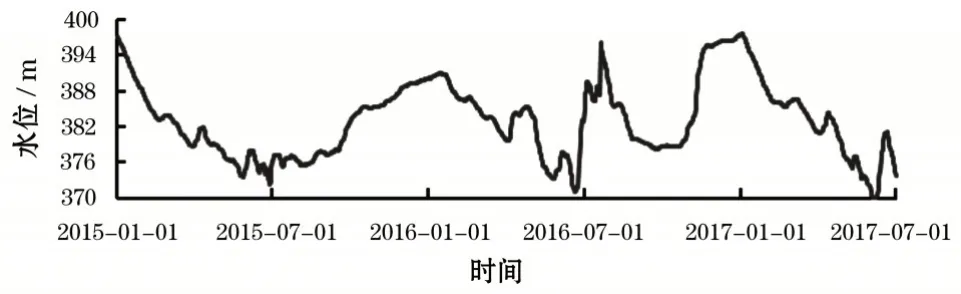
图6 断面的水位过程线

3.2 径流量预测模型计算结果

首先，对径流量进行VMD 分解，从而得到径流量的IMF 分量。径流量的各IMF 分量情况如图7所示。

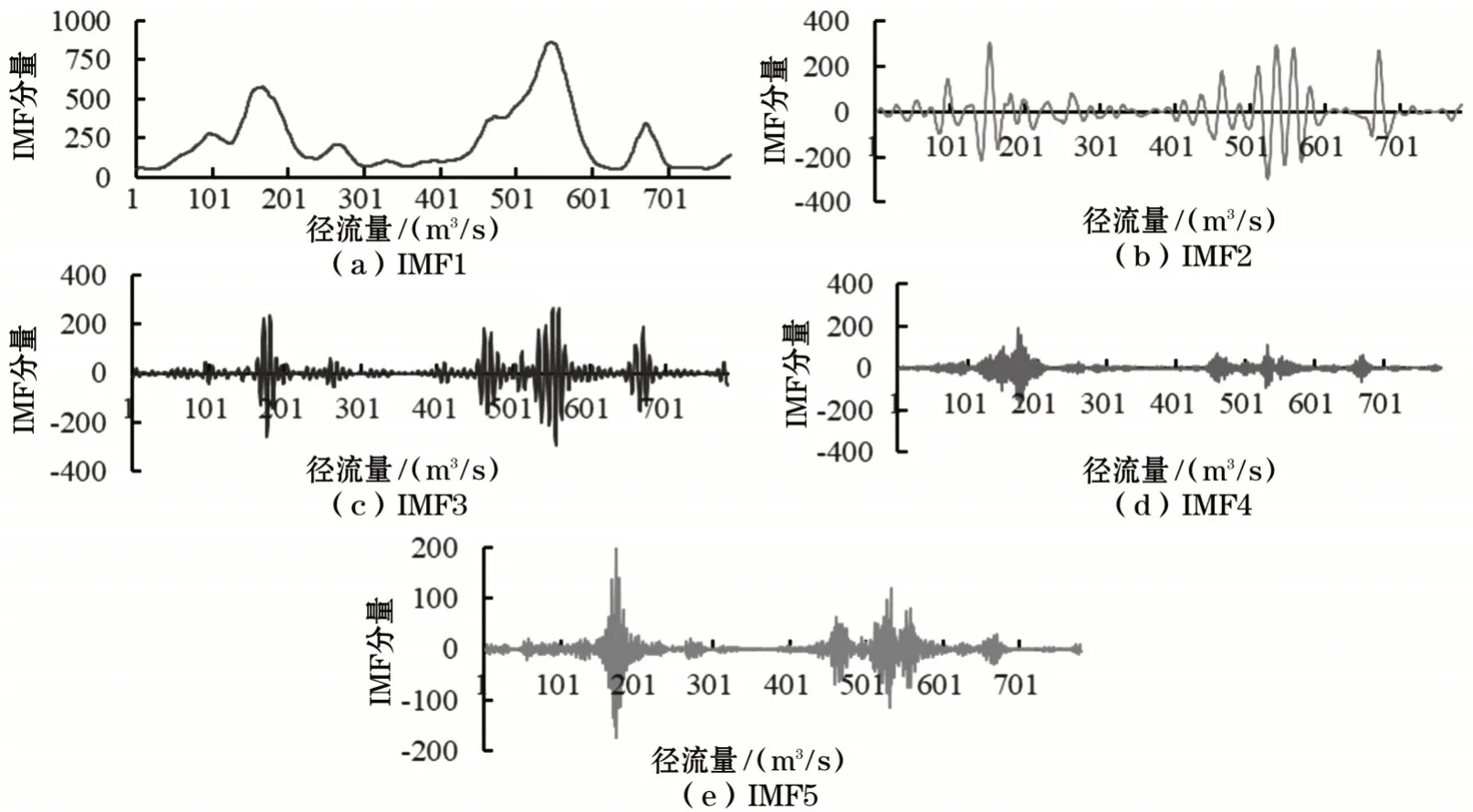
图7 径流量分解的各IMF

采用BiLSTM 算法对径流量的分量IMF1 到IMF5依次进行训练拟合，并将各分量相加得到径流量的拟合值。基于VMD-BiLSTM 预测模型拟合值的决定系数R2为0.99，表明该模型的训练学习能力高，其中该模型的具体拟合值如图8所示。

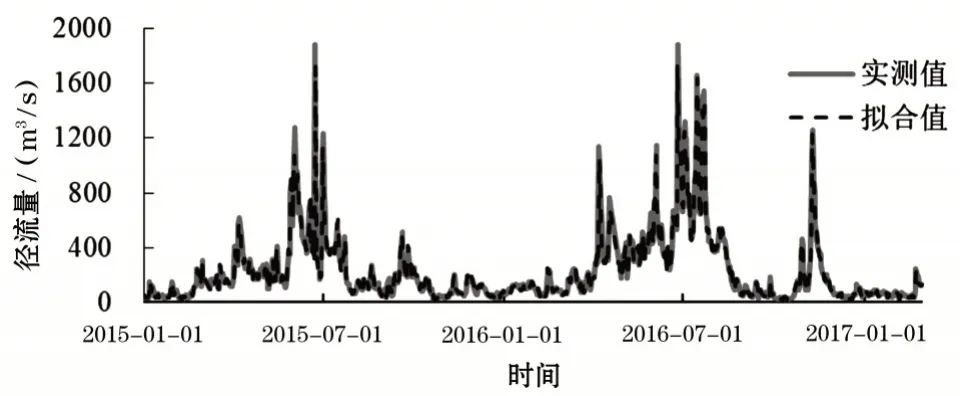
图8 基于VMD-BiLSTM预测模型的径流量拟合值

将预测集的输入变量代入BiLSTM 训练好的各IMF 分量的网络映射模型，则可以得到径流量各分量的预测值。由各分量的预测值相加便得到径流量的预测值，径流量的预测结果如图9 所示以及径流量的预测残差如图10所示。

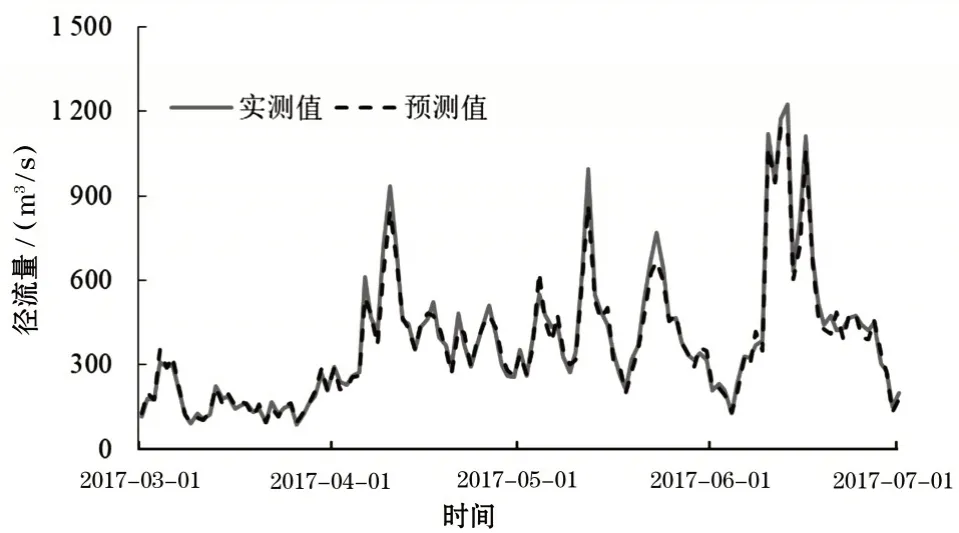
图9 基于VMD-BiLSTM预测模型的径流量预测值

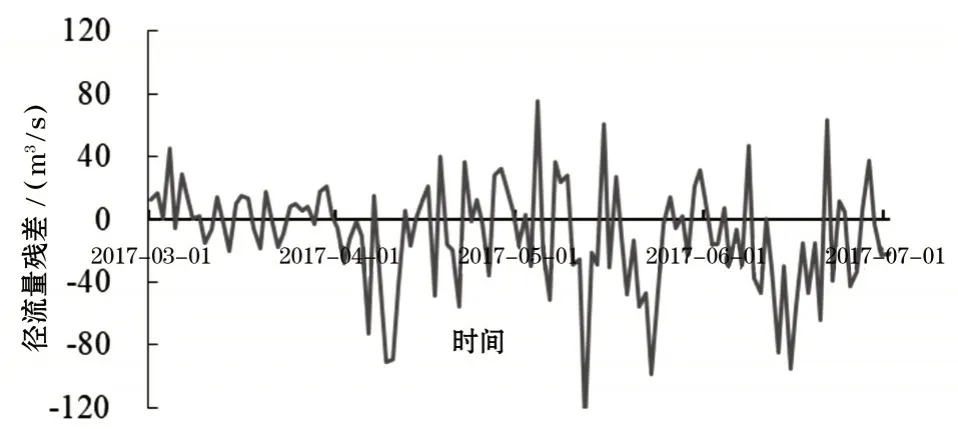
图10 基于VMD-BiLSTM预测模型的径流量预测残差

3.3 预测模型精度分析

为评估和验证VMD-BiLSTM模型的预测精度，同时计算VMD-LSTM模型、BiLSTM模型和LSTM模型的预测值，并与之进行对比。4 个模型的径流量预测结果如图11所示。

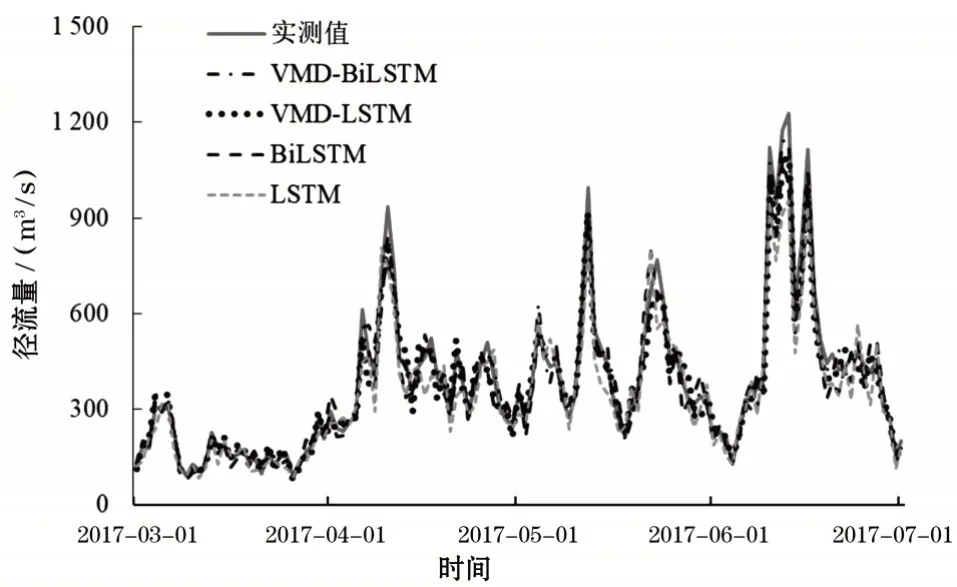
图11 不同模型的径流量预测情况

为评价各预测模型的预测效果，通过以下3 个指标进行计算分析。3个精度评价指标依次为平均绝对误差（MAE）、均方误差（MSE）和平均绝对百分比误差（MAPE），计算方式分别为

式中，xi为径流量的实测值；yi为径流量xi与之对应的预测值。

由图11 和表1 可知：与其他3 个模型对比，VMD-BiLSTM 模型的预测误差最小，精度最高，表明该径流量预测模型具有较高的优越性。VMDBiLSTM 模型比BiLSTM 模型的精度高，表明对径流量进行分量分解可以更好地训练学习各分量的特征，从而提高径流量的预测精度。VMD-BiLSTM 模型比VMD-LSTM 模型的精度提高幅度较大，以及BiLSTM 模型的精度比LSTM模型高，皆说明在考虑径流量时间尺度下的前后影响，径流量预测模型的结果精度可以进一步提高，因此，需要考虑径流量时间效应所产生的作用。

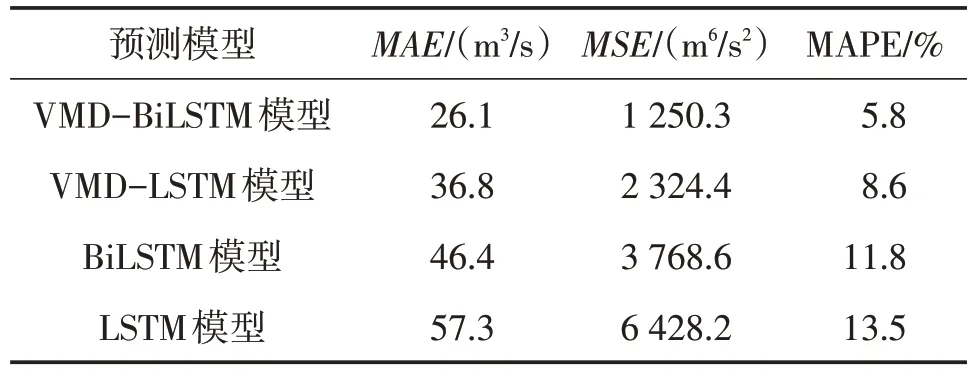
表1 各预测模型的误差情况

4 结 语

本文基于VMD-BiLSTM 构建了径流量预测模型，主要结论如下：

（1）VMD法可以实现对非稳态的径流量进行变量分解，降低直接对径流量分析的难度；优化下的BiLSTM能够对径流量的各IMF进行训练学习，可以得到精度较高的映射网络，从而得到了效果较好的径流量预测模型。

（2）通过工程案例可知，与其他预测模型相比，VMD-BiLSTM 径流量预测模型的精度最高，该模型能够对径流量进行预测，5.8%的误差水平满足工程实践的需要，可以为流域的径流量预测提供新的方法。

（3）本文从数学模型出发，借助深度学习算法建立了径流量预测模型。为了进一步提高预测结果的鲁棒性，可以结合径流量物理模型进行联合预测。