有限域上RSA-ELGamal加密及数字签名方案
杨倩倩,范自强
(安徽理工大学 数学与大数据学院,安徽 淮南,232000)
RSA公钥密码体制是由Rivest[1]等人在1978年提出的,它是公钥密码学中最流行的算法之一,它的安全性在于将大数分解为质因数的困难.攻击者想要分解模数是为了获取私钥.尽管尚未证明大数分解的困难性就等同于RSA算法的安全性,但RSA算法的安全性仍然得到了保证.1985年ELGamal加密体制和数字签名算法被提出[2-3],它的安全性建立在求解离散对数的困难性.这两种公钥体制从提出就被众多学者广泛关注.孙琦在文献[4]中提出了在有限域Fp多项式的RSA加密算法,在代数整数环上定义了陷门单向函数,把RSA在实数域推广到代数数域.曹振富等人[5]指出文献[4]方案中的RSA模拟容易被攻击,提出了一种新的RSA模拟,但存在密文是原来空间两倍的缺点.张斌等人在文献[6]中基于有限域Fp上的多项式性质,对曹振富等人提出的RSA型公钥密码体制进行了修正,提出一种新的改进方法并提出一种新模拟,改进后的体制其明文长度与密文长度相同.这些学者的研究把公钥加密体制推广到更深的层次上[7-8],基于这些方案及结合文献[9]Malhotra的基于增强RSA-ELGamal新加密算法方案,本文提出了有限域上多项式的RSA-ELGamal加密体制.
该体制的安全性是基于两个著名难题的困难IFP与DLP的结合,提高密码加解密计算速度,与有限域上的ELGamal和RSA系统相比,该算法具有更高的安全性.在加密系统中通过引入单向哈希函数,提出了对应的数字签名方案.签名方案的安全性依靠IFP与DLP的困难性和逆函数的难解性,提出的方案也继承了原来体制的优点一次能对多个明文进行加密.
1 预备知识
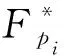

定理1 设g(x)∈Fp1[x]是一个m次多项式,则在Fp1[x]中g(x)可分解为:
(1)

(2)
定理2 设g(x)∈Fp2[x]是一个m次多项式,则在Fp2[x]中g(x)可分解为:
(3)
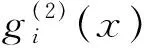
(4)
定理3g(x)∈Fp3[x]设是一个m次多项式,则在Fp3[x]中g(x)可分解为:
(5)
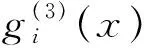
(6)
定理4 设g(x)∈Fq[x]是一个m次多项式,则在Fq[x]中g(x)可分解为:
g(x)=g1(x)g2(x)…gl(x)
(7)
其中:gi(x)为mi次不可约多项式,1≤i≤l.对于∀u(x)∈Fq[x],只要u(x)的次数大于0,并且gcd(u(x),g(x))=1,则[3,12]
u(x)φp(g(x))≡1(modg(x))
(8)
2 有限域上多项式形式的RSA-ELGamal体制
2.1 密钥生成
在Fpi上随机选择m次多项式g(x),要求g(x)在Fpi上可分解为:
(9)

(10)
且通过等式(2)、(4)和(6)可计算φn(g(x)):
(11)
在Fq上随机挑选一个次数小于m次的多项式a(x),满足(g(x),a(x))=1,随机取一个e作为公钥,满足1 d≡e-1mod(φn(g(x))) (12) 再随机选择一个整数k<φq(g(x)),在Fq上计算k(x) k(x)=〈a(x)k〉g(x) (13) 从而该方案的公钥为{q,n,e,φq(g(x)),g(x),a(x),k(x)},私钥为{d,k}. 对任意明文s∈[1,pm-1],将s写成p-adic形式,即s=[ak,ak-1,…,a0]p.令 a(x)=akpk+ak-1pk-1+…+a0=am-1pm-1+…+ ak+1pk+1+akpk+…+a0 (14) 加密者开始对明文m(x)计算: (15) (16) m(x)=〈c2(x)c1(x)-kφq(g(x))〉g(x)=bm-1xm-1+…+bk+1xk+1+bkxk+…+b0 (17) 根据前面提到的明文m(x)的次数m-1小于g(x)的次数m,及(g(x),a(x))=1,从而有下面等式成立. 〈c2(x)c1(x)-kφq(g(x))〉g(x)= 〈m(x)k(x)a(x)e(-kφq(g(x)))〉g(x)= 〈m(x)k(x)a(x)φq(g(x))(-ke)〉g(x) 由a(x)φq(g(x))≡1(modg(x))知,有a(x)eφq(g(x))(-k)(modg(x))≡a(x)(-k). 〈m(x)k(x)a(x)φq(g(x))(-ke)〉g(x)= 〈m(x)k(x)a(x)-k〉g(x)= 〈m(x)a(x)ka(x)-k〉g(x)= 〈m(x)〉g(x)=m(x) 从解密过程的分析可知有限域上多项式形式的RSA-ELGamal公钥体制是可行的. 新方案是基于增强的RSA和ELGamal加密体制,因此方案的安全性也是建立在整数分解问题和离散对数问题.接下来将讨论新方案的安全性.在新方案中,假设在Fq上m次多项式g(x)的次数为1时,g(x)的欧拉函数φq(g(x))=q-1=φ(q).因为a(x)的次数小于g(x)的次数,从而a(x)的次数只能为零,因此多项式a(x)中只剩下常数项a0∈Fq.新体制就变为最初的增强的RSA和ELGamal加密体制,因此,我们提出的有限域多项式RSA-ELGamal公钥体制可以看成是最初增强的RSA和ELGamal加密体制的推广,从而可以得到定理5. 定理5 攻击并打破新体制的难度等价于有限域Fq上最初增强的RSA和ELGamal加密体制的难度. 证明:要证明该定理成立,只需证明当新体制被攻击,有限域Fq上最初增强的RSA和ELGamal加密体制也被成功攻击即可.设最初增强的RSA和ELGamal加密体制的公钥为{n,e,q′,g,K′},私钥为{p1,p2,p3,d,k′},其中:g和k′都是随机数,满足g 本文提出的新方案是在最初增强的RSA和ELGamal加密体制上的推广,其安全性同最初增强的RSA和ELGamal加密体制的安全性一样,增强的RSA比传统的RSA更快地生成私钥和公钥,有更快的加解密速度[10].这两种加密体制的安全性都是建立在大整数素数分解问题和离散对数问题两个难解的问题上.新提出的加密体制在对明文加密时通过引入RSA的公钥对明文进行隐藏加密,而不是直接用私钥进行计算. 假设攻击者想要在加密阶段攻击密文对(c1(x),c2(x)),即使知道c2(x)和k(x),但攻击者并不知道加密者是通过什么方式进行加密的,仍得不到明文.尽管加密后的密文长度也是明文的两倍,但是新方案有高的吞吐量,一次可对多个明文进行加密,减少重复加密的繁琐,加快加解密速度.在新体制中我们用到多项式g(x)要在不同的有限域上有不同的分解式,以及多项式相乘后在取模后g(x)的余项的算法,有限域上的多项式相乘可以转化为向量序列的卷积,可以用快速数论变换进行计算[11]. 在生活中经常会遇到每次要签署多个文件并分发给多个人的情况.目前的数字签名方案基本上都是一次只能对一个消息进行签名,基于有限域上的RSA-ELGamal加密算法方案提出一个具有安全性高的多项式RSA-ELGamal数字签名方案,具有同时加密多个消息功能,提高数字签名的效率[12-13]. 假设A是签名者,Bi(0≤i≤m)是一组不同的签名接收者.A要把不同的待加密文件发给每个Bi,A先给要加密的文件加密,Bi收到A发的加密后的文件和签名后要检验是否是A发送的,并检验文件的真假性. A选取大素数q,有限域Fq上的m次多项式g(x),要满足g(x)的欧拉函数φq(g(x))有大素数因子q1,且m a(x)=〈f(x)φq(g(x))/q1〉g(x) (18) 定理6 在有限域Fq上,有等式〈a(x)q1〉g(x)=1成立. 证明:由定理4知,当(u(x),g(x))=1,∂(u(x))>0,有u(x)φp(g(x))≡1(modg(x)),则〈a(x)q1〉g(x)=〈(f(x)φq(g(x))/q1)q1〉g(x)=〈f(x)φq(g(x))〉g(x),又因为(f(x),g(x))=1,从而有〈a(x)q1〉g(x)=1. 由于有限域Fq上的多项式g(x)的次数为m,从而签名者每次最多可对m个文件进行签名.设A要对t(t≤m)个消息进行签名,分别为n0,n1,…,nt-1.A首先利用哈希函数计算这t个消息的哈希值,记为mi=h(ni)∈Fq1,其中:i=0,1,…,t-1.由上文介绍的多项式和序列是一一对应关系,从而可以把这t个函数值写成多项式形式m(x)各项的系数,即 m(x)=mt-1xt-1+…+m1x+m0 (19) 1)A随机选择s∈Fq,满足(s,φq(g(x)))=1,再计算: l(x)=〈a(x)s〉g(x) (20) 2)将l(x)的系数模上q1,可以得到多项式l′(x),因为g(x)∈Fq,m (21) 是否成立.若成立,则说明签名是有效的;否则签名无效. 〈a(x)cq1a(x)mi〉g(x)=〈a(x)m1〉g(x) 在分析新加密方案时,假设g(x)为有限域上一次多项式,本文提出的方案退化为最初增强的RSA和ELGamal加密体制,我们分析了新加密方案的安全性是建立在整数分解问题和离散对数问题两个难解的问题上的得出定理5[14],即攻击打破新体制的难度等价于攻击有限域Fq上最初增强的RSA和ELGamal加密体制的难度,并给出相应的证明[15].在基于加密体制的数字签名方案中也是如此. 当g(x)为有限域上一次多项式时,此时签名者A只能对一个消息进行签名,不需要把大素数分解为素因子相乘,及在签名过程中生成的多项式h(x),m(x),l(x),v(x)都将变为相应的常数项,从而该签名方案将变为最初增强的RSA和ELGamal数字签名方案.攻击者想要攻击新数字签名方案[16],必须获得签名方案的私钥k,他只能从公开的k(x)或者从A送给Bi的多项式l(x)和l′(x)中求出私钥k,但是攻击者将面临求解离散对数困难问题,所以攻击者无法获得私钥k,从而也无法打破新签名方案,即打破新签名方案的困难性是建立在打破最初增强的RSA和ELGamal数字签名困难性上的. 本文加密算法方案是在有限域上多项式形式基于增强RSA和ELGamal密码体制的难解的问题被提出的,增强的RSA算法依赖于大整数难以素数分解(IFP),在密钥生成中使用三个素数来生成公钥和私钥,它支持更快的加密和解密过程,并比最初RSA更快地生成公钥和私钥.为了提高这些算法的强度,使用了增强RSA和ELGamal的组合,这将提供更高级别的安全性,新提出的是加密体制是一种比现有的多项式形式ELGamal和RSA体制更高效、更安全的系统.在此加密体制的基础上提出有限域多项式形式数字签名算法,相比传统的RSA和ELGamal的签名方案安全性有了很大的提高,在此基础上还可以进一步提出有限域多项式形式的代理签名方案以及代理盲签名方案等,在数据的安全传输、电子银行、电子商务等领域有很广泛的应用.2.2 加密过程
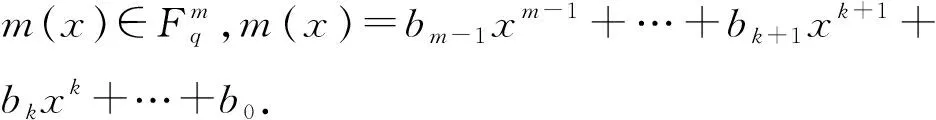

2.3 解密过程
2.4 解密过程的分析
3 方案分析
3.1 对新方案的讨论
3.2 安全性
4 基于新方案的数字签名方案
4.1 系统初始化
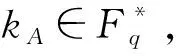
4.2 签名过程

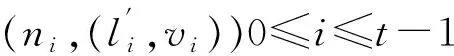
4.3 验证过程

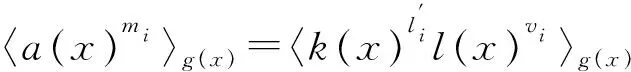
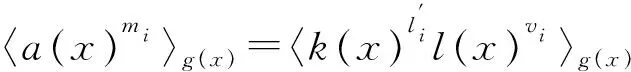
4.4 对新签名方案的安全性分析
5 结 语

