轨宽为1 250 mm且跨度为25 m时跨座式单轨交通的预应力钢筋混凝土轨道梁截面跨高比*
赵军伟 申彦利,2,3 杜 鹏,2,3
(1.河北工程大学土木工程学院, 056038, 邯郸; 2.河北省装配式结构技术创新中心, 056038, 邯郸;3.河北工程大学新型单轨交通体系工程研究中心, 056038, 邯郸)
跨座式单轨交通具有适应陡坡能力强、占地面积少、环境影响小等特点[1]。自重庆轨道交通2号线首次采用跨座式单轨交通制式以来,我国已有多座城市选择跨座式单轨交通作为主要制式[2]。轨道梁是单轨交通系统的重要组成部分,且轨道梁型式与列车构造特点密切相关。
传统跨座式单轨列车采用轮径为800~850 mm的走行轮,并设有稳定轮以保证列车运行的稳定性。相应的轨道梁宽度与列车走行轮间距均为800~850 mm,梁高≥1 200 mm。而最近研发的新型跨座式单轨列车,其导向轮间距增至1 100 mm,且取消了稳定轮。该新型列车载客量可达地铁B型车的运量,最高运行速度提升至100 km/h,更加适合主城区和周边县区的长距离交通需求,且降低了轮胎更换的难度。为适应新型跨座式单轨列车的构造特点,本文研究了相应的新型预应力钢筋混凝土轨道梁(以下简称“新型轨道梁”),并开展了相应的力学性能分析及截面优化研究,为该类轨道梁的进一步研究提供参考。
1 新型轨道梁截面初选和分析方案
1.1 新型轨道梁截面初选
跨座式单轨轨道梁通常采用的PC(预应力钢筋混凝土)轨道梁截面为闭口箱形截面,如图1 a)所示,具有抗弯、抗扭刚度大等特点[3-6]。为适应新型列车的构造特点,本文研究的新型轨道梁跨中截面如图1 b)所示,其初选原则为:①根据新型列车导向轮间距,轨道梁下翼缘宽度取为1 100 mm;②因新型列车取消了稳定轮,故需通过在轨道梁上翼缘两侧设置75 mm宽的外伸段,以保证列车运行的安全性,使轨道梁上翼缘宽度达1 250 mm;③确定轨道梁的高度h,需综合考虑轨道梁刚度、安全及经济等要求,可按(1/20~1/16)l(l为标准跨径)预估[7]。
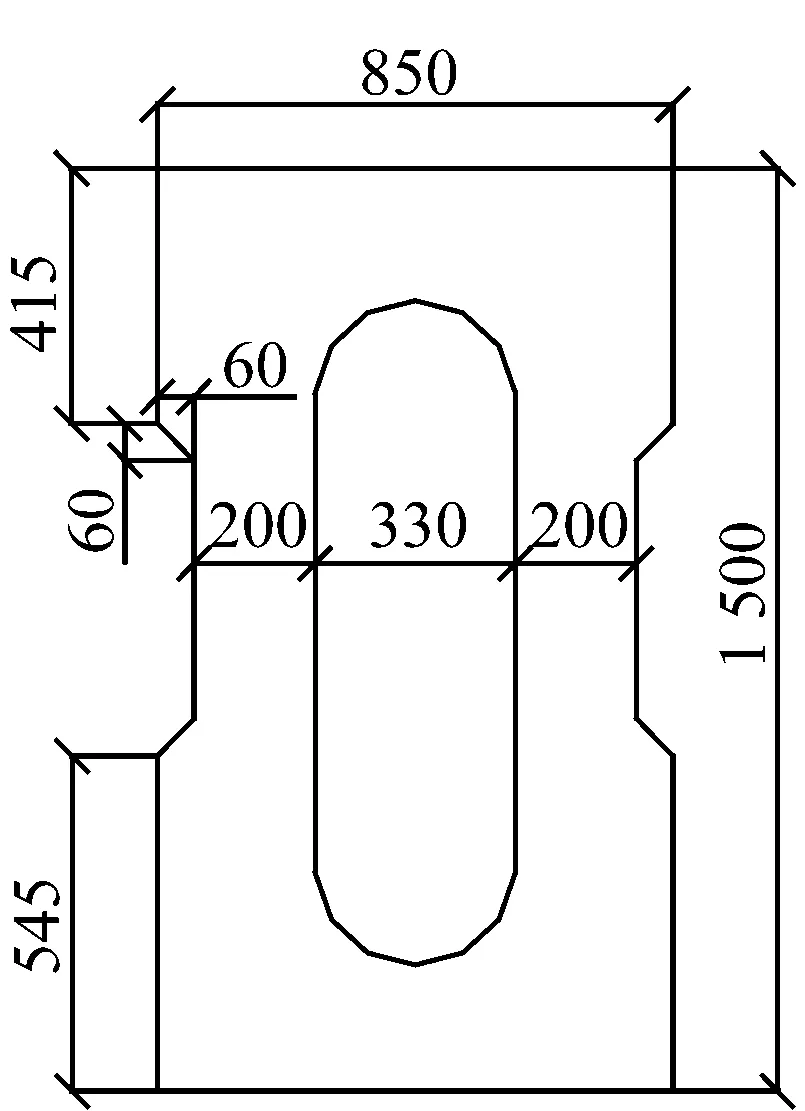
a) PC轨道梁
1.2 静力弹塑性力学分析工况
根据GB 50458—2008《跨座式单轨交通设计规范》[7]及文献[3-6],确定新型轨道梁的静力弹塑性力学分析工况为:工况1(列车静活载),工况2(恒载+列车静活载+列车动力作用+列车横向摇摆力)。
2 新型轨道梁的材料本构模型
2.1 模型主要设计参数和材料
为研究跨高比(l/h)对新型轨道梁受力性能的影响,运用ABAQUS软件建立新型轨道梁材料本构有限元模型(以下简称“新型轨道梁模型”)。为验证新型轨道梁模型的准确性,本文选择文献[8]的模型作为比较对象。为此新型轨道梁模型及参数取值均同文献[8]的模型对照。
该计算忽略其他因素如钢筋型号、混凝土型号等对新型轨道梁力学性能的影响,只改变跨高比,不改变配筋、配筋截面积及预应力筋等参数。按一般轨道梁尺寸,并参照文献[8]的模型,建立跨长均为25 m,而梁高不同的8个新型轨道梁模型进行计算。按相关规范的规定,跨高比分别取15.6、16.1、16.6、17.2、17.8、18.5、19.2、20.0,相应的梁高取值范围为1 250~1 600 mm,取值间隔为50 mm。8个不同梁高的新型轨道梁模型编号分别为YL1、YL2、YL3、YL4、YL5、YL6、YL7、YL8。新型轨道梁模型的主要配筋情况如表1所示。其中典型的模型YL3配筋设计,如图2所示。
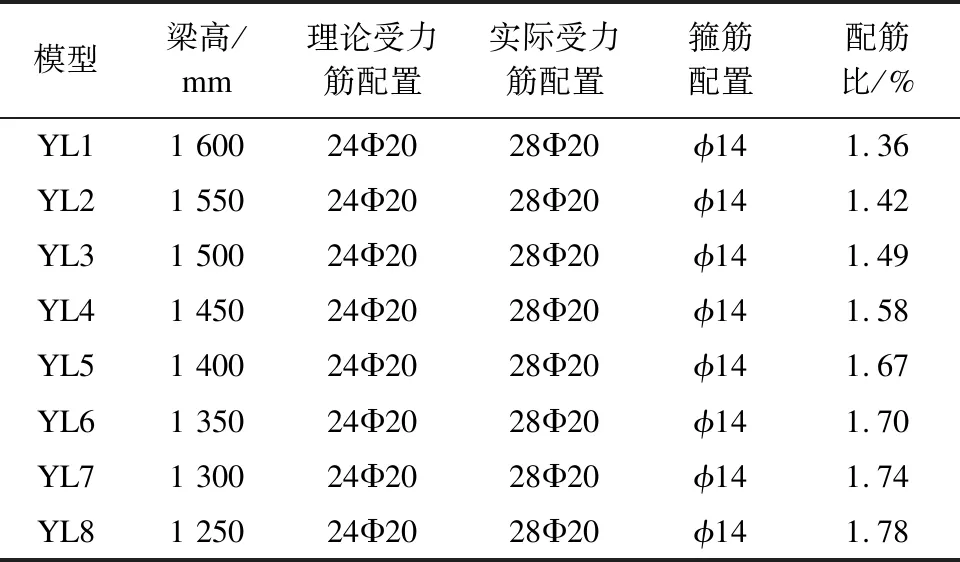
表1 新型轨道梁模型的主要配筋情况
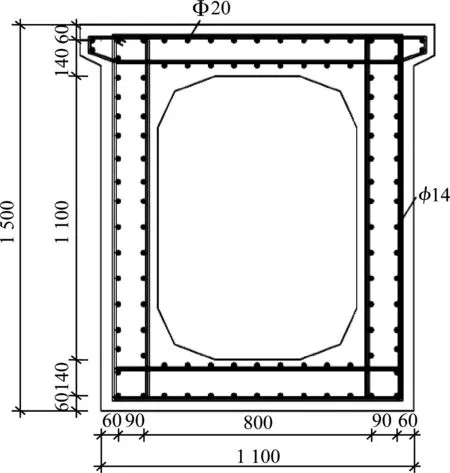
单位:mm
在新型轨道梁模型中:纵向受拉非预应力筋材料为HRB400,箍筋材料为HPB300;新型轨道梁在纯弯段范围内的箍筋间距为200 mm,在非纯弯段的箍筋间距为150 mm,在梁端部的箍筋间距为100 mm;每组预应力筋束由3束预应力钢绞线组成,采用直线布置;预应力钢绞线为1束7根标准型φ15.24 mm低松弛钢绞线。
根据TB 10092—2017《铁路桥涵混凝土结构设计规范》[9]计算新型轨道梁预应力损失。经计算,预应力的损失应力为195.0 MPa。又因预应力筋束在新型轨道梁端部锚下的控制应力σcon为1 395 MPa,故建模时通过降温法[8]计算可得,降温512.82 ℃ 能达到有效预应力1 200.0 MPa的要求。
2.2 接触关系与边界条件
在新型轨道梁模型中,假定忽略混凝土同钢筋及预应力钢绞线之间的粘结滑移,采用Embedded Region约束,将钢筋骨架和预应力钢绞线嵌入到整个模型中,并将支座处的垫块与混凝土接触面设置为绑定约束。
新型轨道梁模型的边界条件:一端选用固定铰支座,限制x、y、z方向(横向、纵向、竖向)的位移;另一端选用滚动铰支座,限制y、z方向(纵向及竖向)的位移。两端皆不限制y、z方向的转动自由度。
2.3 新型轨道梁模型的结果验证
在简支梁三分点处加载,以跨中截面最大位移为计算对象,得到跨中截面的荷载-位移曲线对比图,如图3所示。由图3可知,模拟结果与试验结果的荷载-位移曲线拟合较好。
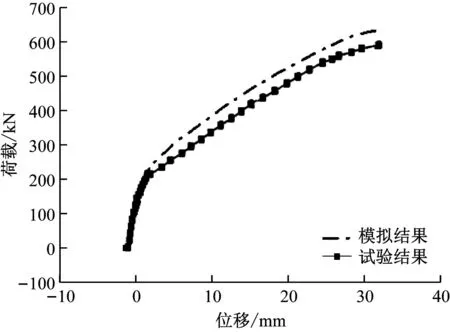
注:试验模型极限荷载=580 kN;模拟模型极限荷载=610 kN;理论计算极限荷载=592 kN。
通过新型轨道梁模型模拟得到轨道梁开裂荷载和极限荷载的模拟值。为验证新型轨道梁模型的计算准确性,将新型轨道梁模型的模拟值、文献[8]中的试验值及按理论公式计算得到的理论值进行对比,结果如表2所示。
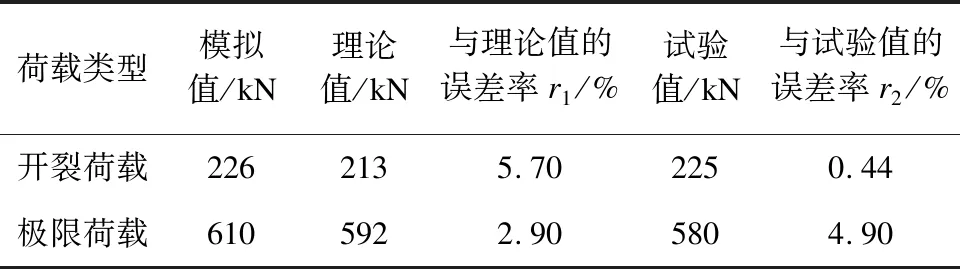
表2 不同类型荷载的模拟值、理论值及试验值对比
由表2可以看出,极限承载力模拟值略高于试验值和理论值,混凝土开裂点也略晚于试验所测结果。经分析,出现此现象的原因是:试验设计材料C50混凝土的实际测得混凝土轴心抗压强度为35.11 MPa,而在数值模拟中C50混凝土的轴心抗压强度取值为35.50 MPa,取值存在的误差导致计算结果的误差。但计算结果的最大误差仅为5.7%,说明模拟结果、试验结果及理论计算结果均基本吻合。
3 新型轨道梁的受力性能
本文应用新型轨道梁模型对工况1下的跨中挠度、工况2下的跨中截面应力和刚度进行模拟计算,进而分析新型轨道梁的受力性能。
3.1 工况1下的跨中挠度
在工况1下,不同跨高比新型轨道梁的跨中截面挠度如表3所示。由表3可知:在工况1荷载作用下,当跨高比为20.0时,新型轨道梁模型计算所得挠度最大,为9.60 mm,满足《跨座式单轨交通规范》[7]中的竖向挠度应不超过l/800的要求。跨中挠度随轨道梁跨高比增大而增大,分析认为轨道梁梁高的下降会引起截面惯性矩的减小,而惯性矩的减小会导致抗弯刚度的降低,刚度的降低又会导致挠度的增大,故跨中挠度随着轨道梁跨高比的增大而增大。
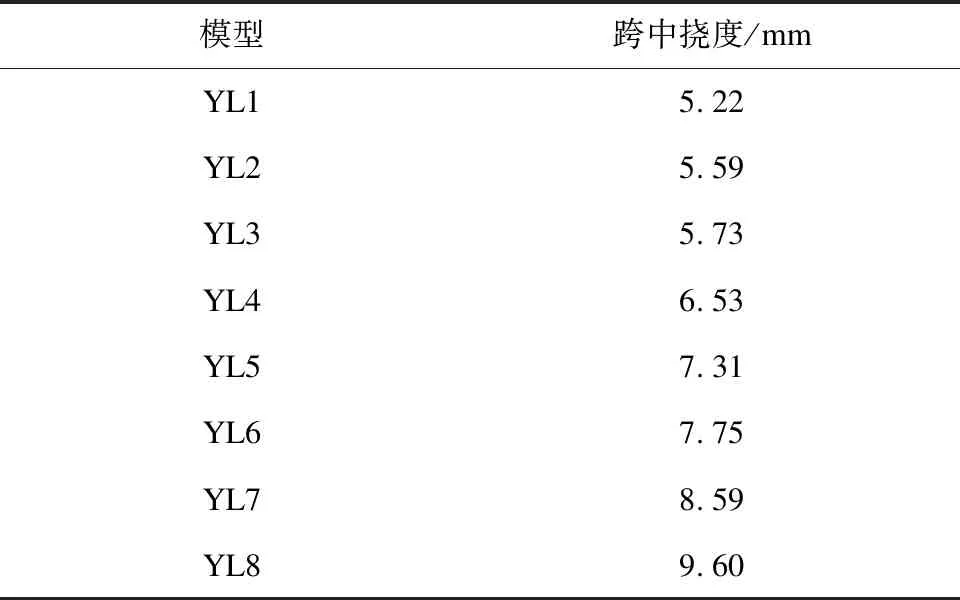
表3 工况1新型轨道梁跨中挠度
3.2 工况2下的跨中截面应力
跨中截面应力选择轨道梁跨中截面四角点(如图4中的A、B、C、D点)处的应力进行分析。在工况2下,不同跨高比新型轨道梁的跨中截面四角点混凝土应力模拟计算结果,如图5所示。
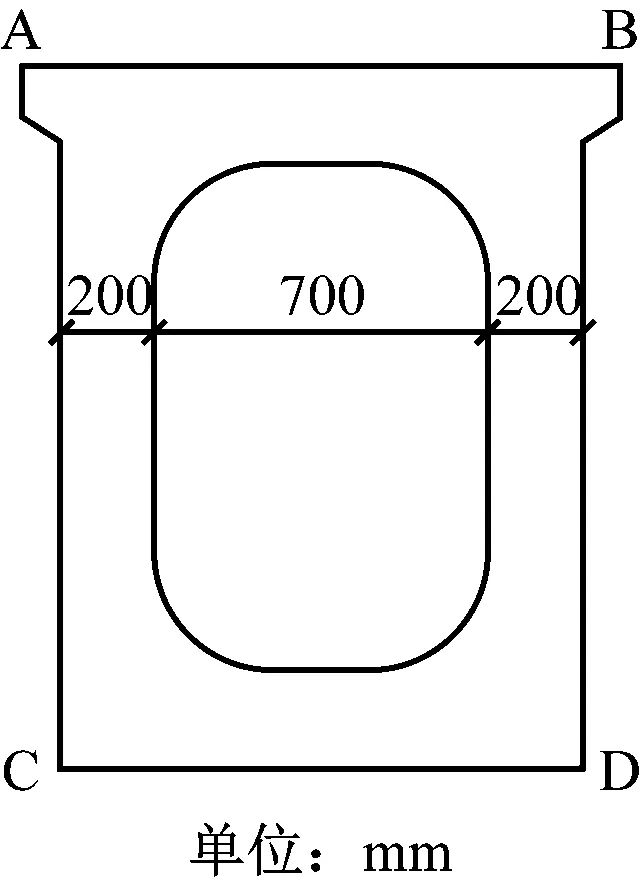
图4 轨道梁跨中截面的四角点示意图
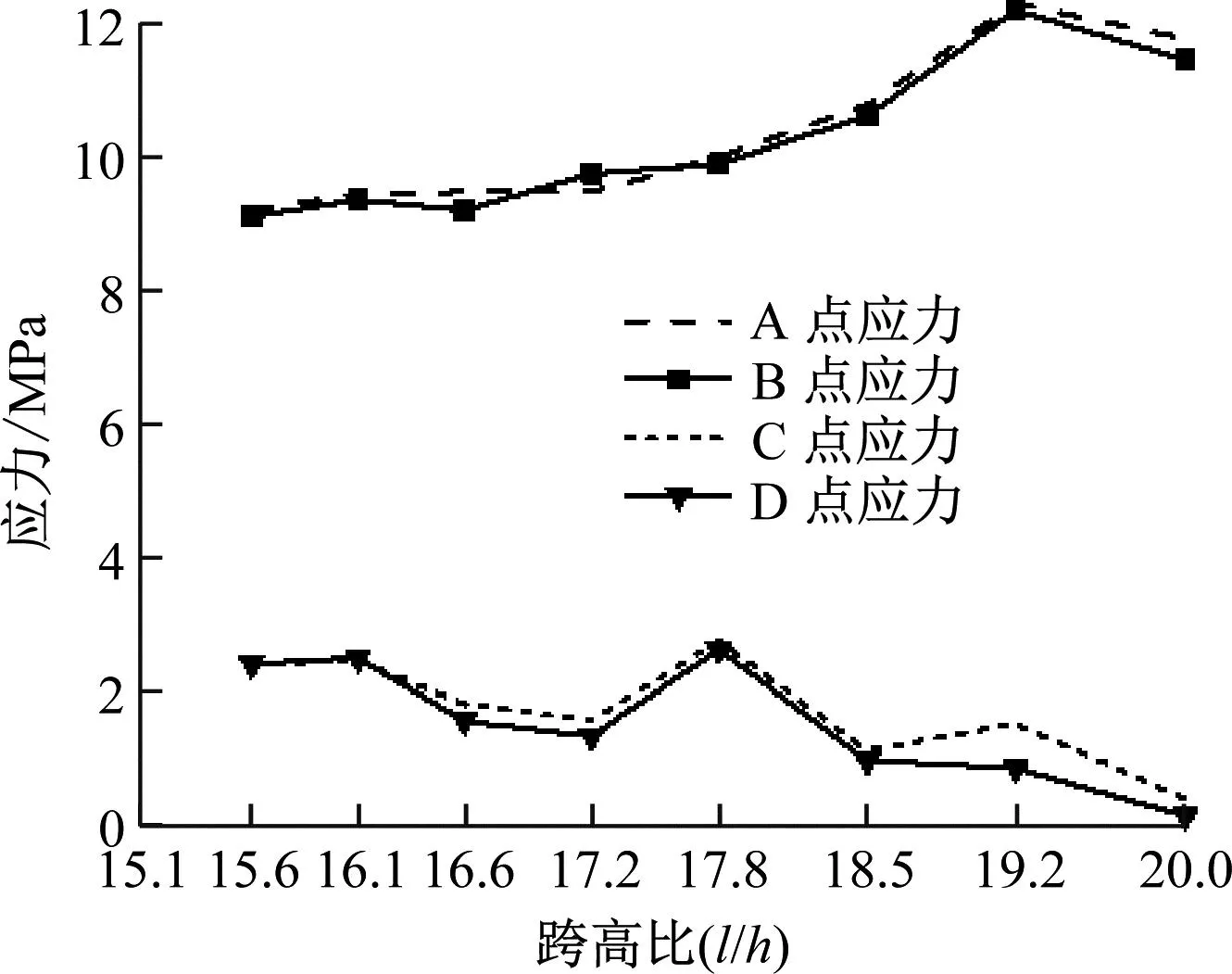
图5 工况2下跨中截面四角点的混凝土应力
由图5可知, 新型轨道梁的跨中截面四角点混凝土压应力最大值位于左上角点(A点),σcp<15 MPa,小于混凝土容许压应力σc=23.925 MPa,而且未出现拉应力,满足国家标准TB 10092—2017《铁路桥涵梁混凝土结构设计规范》[9]文中关于混凝土容许压应力和容许拉应力的规定。
3.3 工况2下的刚度分析
经模拟计算,工况2下新型轨道梁的刚度变化情况如表4所示,混凝土开裂荷载及跨中截面钢筋应力如表5所示。
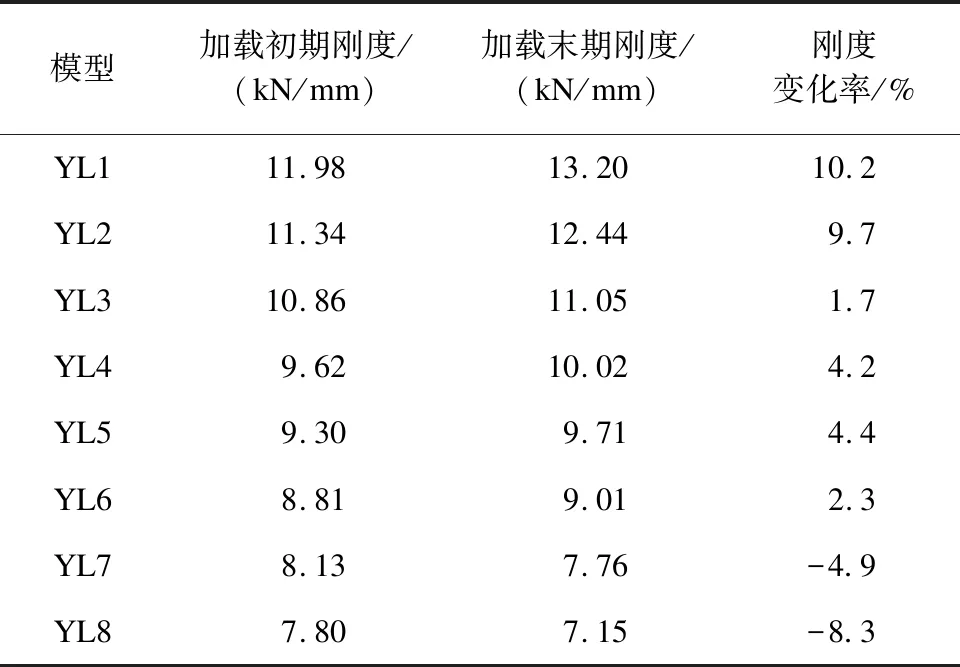
表4 工况2下新型轨道梁的刚度变化情况
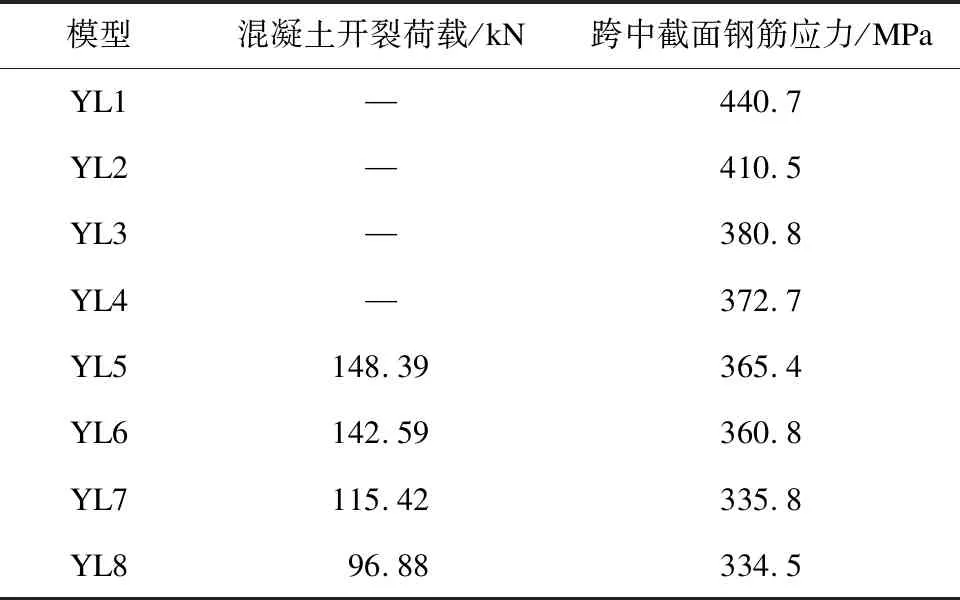
表5 工况2下的混凝土开裂荷载及跨中截面钢筋应力
由表4及表5可知:当轨道梁宽高比为15.6及16.1时,刚度变化率约为10%,刚度变化较小,且混凝土未开裂,说明轨道梁处于弹性阶段,但钢筋屈服,继续加载轨道梁将发生脆性破坏;当轨道梁跨高比为16.6及17.2时,刚度变化率为5%以下,刚度变化较小,并且混凝土未开裂、钢筋未屈服,说明轨道梁处于弹塑性阶段,继续加载轨道梁将延性破坏;当轨道梁跨高比为17.8及18.5时,刚度变化率为5%以下,混凝土开裂,但钢筋未屈服,说明轨道梁处于弹塑性阶段,继续加载轨道梁将延性破坏;当轨道梁跨高比为19.2及20.0时,刚度变化率为负数,混凝土开裂且钢筋未屈服,但此时的轨道梁截面高度高,相对工程造价高、施工难度较大。
综上所述,当轨道梁跨高比为16.6~18.5时,新型轨道梁的受力性能较好,工程造价相对较低,施工难度适宜。
4 结语
1) 为针对新型跨座式单轨列车的需求而设计的跨度为25 m的新型轨道梁,通过静力模拟分析轨道梁的跨中挠度、应力、加载初期刚度与加载结束刚度的变化等结果,验证新型轨道梁的力学性能均满足规范要求。
2) 通过模拟分析不同跨高比下的新型轨道梁在静力荷载下的力学性能,发现跨高比为16.6~18.5时,25 m跨度的新型轨道梁的力学性能较好,且造价适宜、施工难度较低,对于新型跨座式单轨轨道梁的进一步研究具有一定的参考意义。

