转向节锥面球头销装配力矩衰减研究
程稳正 苟黎刚 余小巧 张俊 宋子华
(吉利汽车研究院(宁波)有限公司,宁波315000)
1 前言
锥面球头销是悬架系统中常见的连接方式,如果装配力矩设定不合理,会导致连接部位松动异响,严重的会导致球销断裂,发生安全事故[1-2]。目前国内外普通螺栓紧固连接设计多根据相关设计准则进行理论计算[3-6],基于简化模型,根据工作外载及抗滑移系数要求计算所需预紧轴向力,再通过接头试验确定拧紧力矩及拧紧工艺。运用设计准则评估连接的可靠性,关键是模型简化、工作外载确定、连接件和被夹持件刚度计算[7]。锥面球头销不同于普通螺栓连接,结构复杂刚度值难以获取,受力模型不符合标准适用范围,理论计算实施受限,需要结合仿真手段。对于普通螺栓连接,众多学者进行了仿真研究[8-10],考虑结构、材料特性、装配公差、接触状态的影响,对设计准则局限性进行了有益补充。
通过仿真手段研究了锥面球头销结构屈服导致的力矩衰减问题。针对某乘用车在试车场试验中,转向节与下摆臂锥面球头销连接松动异响的现象,提出基于仿真分析的装配力矩设定方法,可以规避传统基于设计准则方法的不足,有效解决了路试异响问题,并推广至结构优化应用,提升了锥面球头销连接的可靠性。
2 球头连接
2.1 连接结构
以麦弗逊式悬架的前转向节与下摆臂的锥面球头销为研究对象,总成结构如图1 所示,为了便于观察,隐去了球头防尘罩。

图1 连接结构
局部剖面如图2 所示,球头销为1∶6 的锥面球头销,夹持面距离为22 mm,转向节材料为QT450,球头销材料为42CrMo,螺母材料为SWRCH35K。按初始的拧紧工艺测试得到的球头销装配预紧力为16 kN。

图2 局部剖面
该车辆在盐城试车场进行耐久路试时,发生敲击异响,经过声音探测,确认异响来自转向节与下摆臂球头销连接部位。
2.2 异响原因
球销异响原因通常有2 种,一种是异物进入导致的非正常磨损,另一种是连接松动[11-12]。经拆解,球头销未发现异常磨损,可判定原因为连接松动。
普通螺栓装配连接可以简化为2 个平衡的弹簧结构,如图3 所示,弹簧为被夹持件,中间的弹簧为连接紧固件,拧紧时螺栓拉伸伸长,被夹持件压缩变短,二者的弹性恢复力相互平衡,锥面球头销装配受力原理的不同之处在于,普通螺栓连接依靠螺栓头与螺母之间被夹持件提供弹性恢复力平衡螺栓伸长的恢复力,而锥面球头销连接依靠锥面抱紧力的分力平衡球销伸长的恢复力。

图3 预紧力
研究表明:被联接件发生塑性变形是造成螺栓连接松动的重要原因之一,由于存在塑性变形,弹性恢复力降低,外在表现为预紧力衰减[13-16]。
图4 为典型的螺栓连接刚度三角形,假设夹持件刚度为Kb,被夹持件刚度为Ks,二者发生弹性变形而平衡,平衡位置的预紧力为F0;当连接发生溃缩永久变形量为δ,二者重新平衡后的预紧力变化为F1,F1<F0,表明预紧力发生衰减,发生衰减后,实际的预紧力减小至F1,如果的预紧力F1不能满足外载工作要求,则会导致松动。
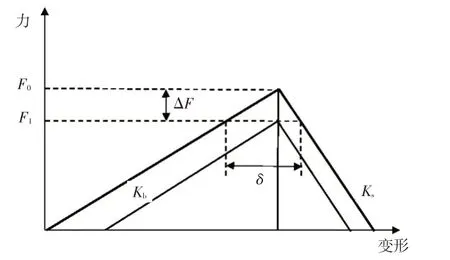
图4 预紧力衰减
当球头销受到径向力F时,接触面有分离的趋势(图5),当径向力足够大时,接触面会发生分离,当径向力减小时,接触面恢复至贴合状态,因此,造成松动异响的原因为冲击过载时接触面发生分离,在冲击载荷消退时,由于零件弹性的快速恢复发生敲击,外在表现为异响。

图5 连接变形(×50)
为此,从2 个方面开展仿真分析,一是极值载荷作用条件下的接触面积变化情况,二是在交变载荷作用条件下,预紧力的衰减情况。
3 预紧力设定
3.1 设定流程
为解决球头连接异响问题,首先根据路谱载荷极值,仿真不同预紧力条件下球头销装配接触面积的变化趋势,找出临界预紧力;其次,将仿真交变载荷作用下的残余预紧力控制在临界预紧力之上,以规避接触面分离过大导致的异响;最后通过接头试验确定拧紧工艺,具体的工作流程如图6所示。
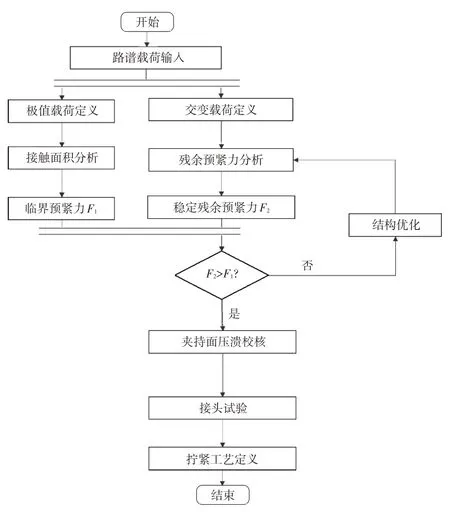
图6 设定流程
3.2 极值载荷
路谱载荷来自虚拟试车场(Virtual Proving Ground,VPG)仿真,共计23 条路面,得到球头局部坐标系下的路谱载荷Fx、Fy和Fz,分别为2 个径向力和一个轴向力,如图7 所示,径向力分力较大,而轴向力很小,因此可以忽略轴向力的作用。
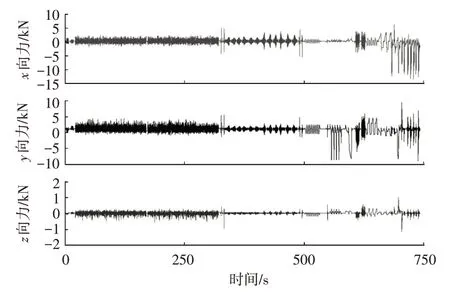
图7 球头三分力
根据平面力合成,求得径向合力的历程,经过穿级计数统计得到如图8 所示的载荷频次。由图8 可知,最大径向力合力约为14 kN,在此载荷作用下结构局部是否发生屈服需经过仿真确认。由于转向节锥面孔为圆形结构,在过载情况下圆孔有变扁的趋势(图9),因此,需要重点关注最大径向力合力方向轴上的反向载荷。
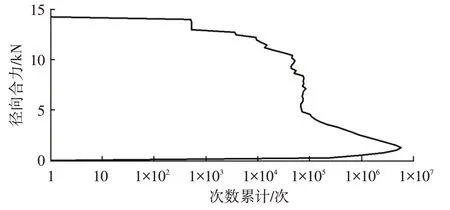
图8 径向力穿级计数
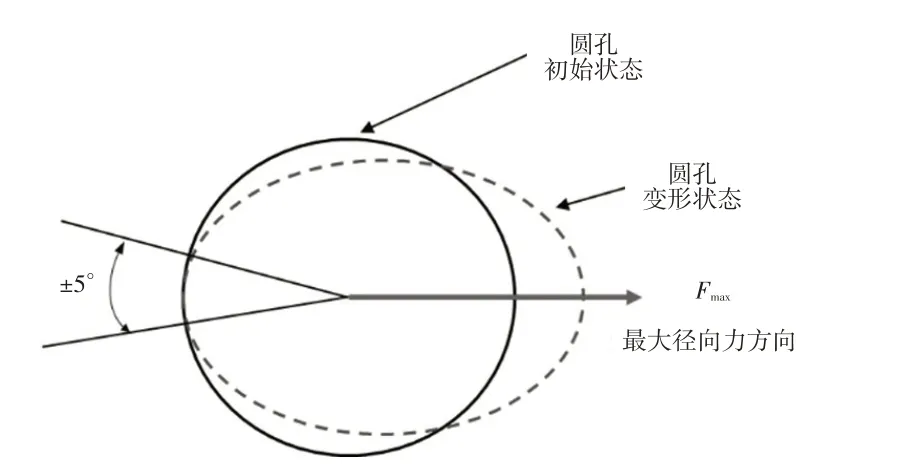
图9 交变载荷方向
以合力最大载荷为主受力方向,求其反方向的最大载荷作为交变载荷;根据最大合力的2 个分力,求得载荷角度反方向±5°范围内合力的最大值及其2 个分力值,计算方法如下:
式中:Fx(t) 、Fy(t) 分别为球头的2 个载荷分量历程,Fres(t)为合力历程,Fres(t0)为正向合力最大值,θ为正向合力最大值角度,Fx(t0)为径向力合力最大值时刻x向分力,Fy(t0)为径向力合力最大值时刻y向分力,α(t)为载荷角度历程,Fr′es(t)为反向角度范围内合力历程,Fres(t1) 为反向合力最大值。
求得反向载荷合力最大值(图10),根据角度方向进行分解,得到的最终载荷条件如表1 所示,仿真分析分2 个载荷工况,工况1 为极值载荷,观察接触情况;工况2 为交变载荷,观察预紧力衰减情况。

表1 极值载荷

图10 反向合力最大值
3.3 仿真模型
建立锥面球头连接装配模型,包括螺母(1)、转向节(2)、锥面球头销(3),为精细计算接触力,转向节局部采用六面体网格(4),转向节其它部分和螺母采用二阶四面体建模。表2 为各个部件之间的接触关系定义,计算模型如图11 所示。

表2 接触定义

图11 仿真模型
3.4 临界预紧力
约束截取的转向节,在球头中心点位置施加极值载荷,输出接触面积,计算不同预紧力条件下的接触状态变化。每种预紧力条件下,分为2 个载荷步计算,载荷步1 施加预紧力,载荷步2 施加极值载荷(表1 中工况1),通过约束预紧力截面自由度实现预紧力跟随外载变化。图12~图16 为接触压应力的变化情况,面压小于0.1 MPa 可认为接触面存在分离,即图中的深色区域,接触面压大于0.1 MPa 可认为接触面贴合。

图12 预紧力16 kN接触面压强

图13 预紧力20 kN接触面压强

图14 预紧力25 kN接触面压强

图15 预紧力30 kN接触面压强

图16 预紧力35 kN接触面压强
由图12~图16 可知,在外载作用下接触面存在分离情况,当预紧力小于20 kN 时,上下两侧均存在分离,即球头销与转向节锥面之间的装配面被撬开,一旦冲击载荷变小,零件因自身弹性快速恢复,导致敲击,外在表现为异响。当预紧力大于25 kN 时,接触面分离现象逐步减弱,但始终存在部分区域分离,这是由于转向节、球头销均为弹性体,在极大载荷的作用下很难完全不分离,只是分离的区域在逐步减小。
表3 为不同预紧力条件下的接触面积变化情况,当预紧力小于25 kN 时,接触面积随预紧力的增加快速增加,当预紧力达到25 kN 后,接触面积的增加幅度放缓,据此判断预紧力25 kN 为临界载荷,即拧紧装配产生的预紧力要大于25 kN。
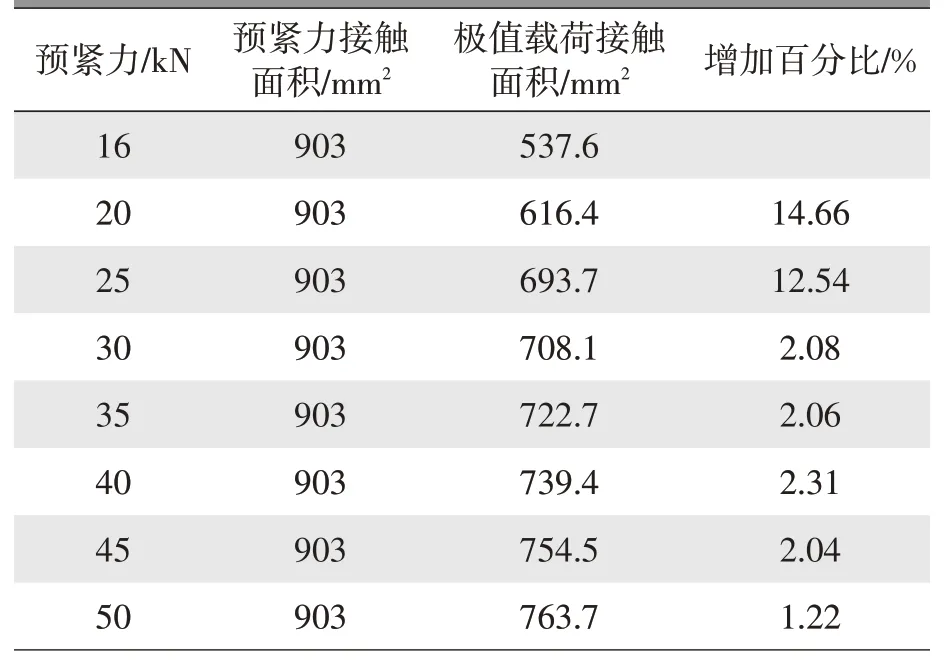
表3 接触面积
3.5 预紧力衰减
如上文所述,在冲击过载作用下,如果连接部位结构局部发生屈服,会导致弹性恢复力降低从而引起预紧力降低。计算分析模型中考虑材料非线性和几何非线性,利用表1 中工况1 和工况2 定义交变载荷周期,观察预紧力的衰减情况。
图17为预紧力为16 kN、极值载荷作用下的塑性应变分布,可以看到转向节在锥面孔附近存在局部屈服,图18为材料屈服对预紧力的影响,同样载荷条件作用下,线弹性材料的残余预紧力最小值为7.74 kN,考虑材料屈服的残余预紧力最小值为7.03 kN,预紧力减小9.2%,表明材料屈服会导致预紧力衰减。

图17 局部塑性应变
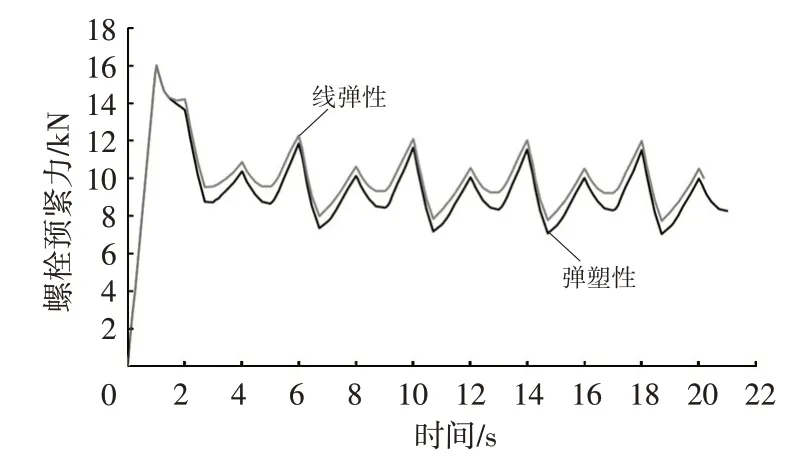
图18 结构屈服对预紧力的影响
图19 分别为预紧力为16 kN、30 kN 及40 kN时,在交变载荷条件下预紧力的变化情况。在外载作用下,预紧力存在波动,预紧力的下限值表示锥面球头销在外载荷变化下的实际最小预紧力值,因此预紧力的下限值需要大于临界预紧力值才能防止接触面大面积的撬开,从而防止异响发生。

图19 预紧力波动
表4 为在交变载荷作用下,不同初始预紧力情况下预紧力下限值的对比情况,当预紧力达到40 kN时,下限值可以达到约25 kN,满足临界预紧力要求,因此,可将预紧力目标要求设定为大于40 kN。
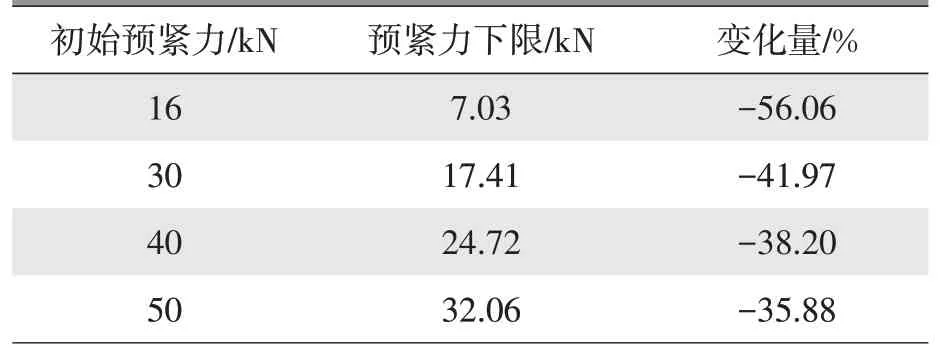
表4 预紧力下限
3.6 压溃力校核
在进行被连接件失效分析时,需要保证连接承压面不发生压溃或塑性变形,即:
式中:Fmax为最大载荷,[σ]为许用应力,A为承压面积。
转向节材质为QT450,屈服应力为310 MPa,支承面面积为145 mm2,根据应力和面积计算出屈服压溃力为45 kN,因此,40 kN 预紧力满足压溃校核要求。
由于转向节材料的屈服极限远低于球销和螺母,施加预紧力后需要校核预紧力作用下锥面的压溃情况。图20 所示为节点接触面压分布,由于接触局部的非线性,导致在接触面的边缘部位出现严重的面压不连续情况,局部面压达到588 MPa,与实际结构物理表现不符,为此采用平均面压进行校核。
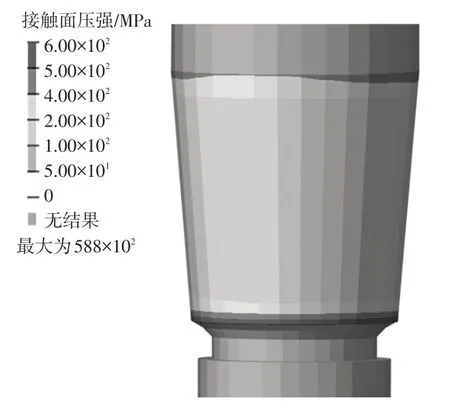
图20 接触面压分布
平均法向压应力计算如下:
式中:Pnormal为平均法向压应力,CPRESSi为节点法向压强,n为接触面节点数。
不同初始预紧力条件下的计算结果如表5 所示,预紧力为40 kN 时面压为206 MPa,小于QT450材料屈服极限310 MPa,不会产生压溃。引申至铝合金转向节,比如A356 材料转向节,其屈服极限为220 MPa,当预紧力超过45 kN 时,面压超过材料屈服极限,这时需要附加钢套,因此,接触面压的校核是拧紧力矩设定过程中不可忽视的环节。

表5 平均压应力
3.7 接头试验
按照预紧力目标40 kN,可以通过模拟接头试验进行拧紧工艺的定义。通常的接头试验分为3 步:
a. 在螺栓或球头销端头布置压电陶瓷片,测量球头销的伸长量;
b. 在螺栓性能试验机上进行轴向力标定,得到球头销长度变化量与轴力的关系曲线;
c. 利用立式模拟拧紧设备进行装配试验,记录拧紧过程中的扭矩、转角和伸长量数据,根据标定得到伸长量与轴向载荷的关系,进而得到扭矩-转角-轴力的关系,最终确定拧紧工艺。
由于锥面球头销在拧紧过程中,在抱紧力作用下,球头锥面和转向节锥面之间发生类似过盈装配的情况,难以拆卸,导致球销伸长量无法准确测量,常规方法无法使用,因此,提出基于扭矩曲线评估实际轴向力的方法。
扭矩示意见图21,在拧紧设备上模拟装配,记录拧紧力矩曲线,找到屈服扭矩T0,结合球销的拉伸屈服与轴向力对应关系,找到屈服轴向力F0,根据目标轴向力F1,计算拧紧扭矩T1,计算方法如下:

图21 扭矩示意
重新设置拧紧力矩后的球销连接,在后续的试车场试验中没有出现异响,成功解决。
3.8 结构优化案例
某车型转向节在进行强度试验时,发生装配力矩衰减。该转向节为铝合金铸造转向节,为防止预紧力压溃,球销与转向节之间采用压入钢套,装配模型如图22 所示,台架试验力矩衰减情况如表6 所示,力矩平均衰减值达到50.9%,存在风险,采用本研究方法进行仿真分析。
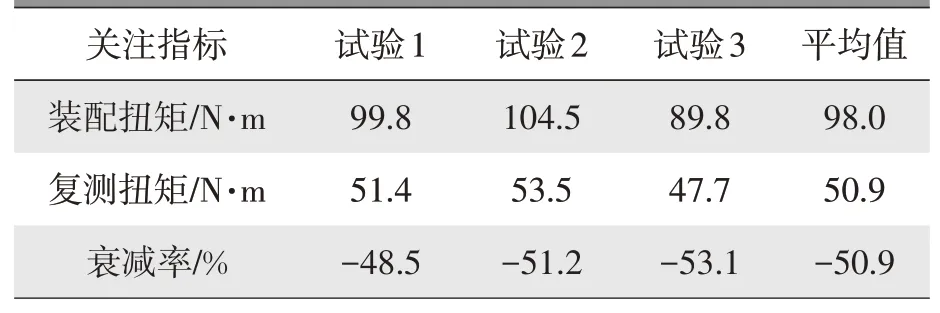
表6 试验结果

图22 仿真模型剖面
施加极限载荷后的塑性应变分布如图23 所示,钢套、转向节局部发生屈服,如前文所述,在交变载荷作用下引起弹性恢复力降低导致力矩衰减。

图23 原结构塑性应变
针对预紧力衰减的情况,根据塑性应变分布情况提出2 种优化方案,方案对比如图24 所示。

图24 优化方案示意
a.优化方案1:增加钢套法兰面厚度,由2.5 mm增加至4.5 mm。
b. 优化方案2:增加钢套外径,由23 mm 增加至26 mm。
图25、图26 分别为2 种优化方案极值载荷作用下的塑性应变分布,优化方案1 钢套的屈服区域明显减少,有利于减少力矩衰减。施加交变载荷后,螺栓预紧力变化仿真结果如表7 所示,原始方案衰减最明显,优化方案1 效果最好,相对原始方案提升了44.9%,结合原始方案的试验结果、仿真结果对比,判断优化方案1 可以满足要求。优化方案1 最终的试验结果力矩衰减了34%,满足力矩衰减小于40%的设计目标。

表7 仿真结果
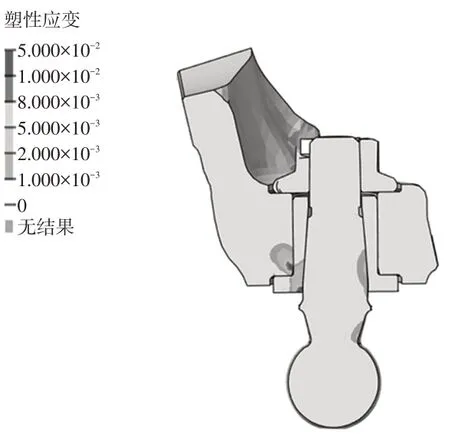
图25 优化方案1塑性应变
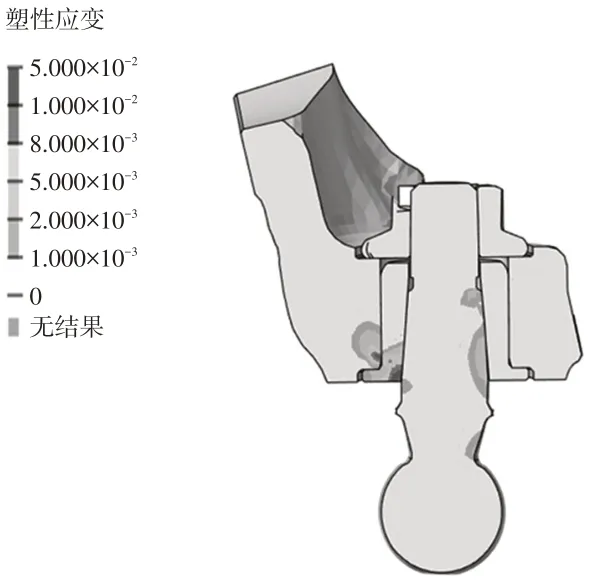
图26 优化方案2塑性应变
由表6、表7 对比可知,衰减率仿真结果与实际试验结果存在一定偏差,原因如下:一是材料的应力应变,为安全起见,一般根据材料标准采用性能下限,与零件实际材料性能有偏差;二是仿真模型没有考虑螺母和球销螺纹啮合的影响,而是采用绑定接触进行简化处理;三是仿真模型没有考虑转向节锥面孔和球销锥面几何尺寸公差,直接影响装配预紧力。但在相同的条件下,可以评判仿真结果的趋势,物理验证是常用的工程问题解决方法。
4 结论
以麦弗逊式前悬架的转向节与下摆臂连接锥面球头销为研究对象,通过仿真分析设定了拧紧力矩,解决了路试异响的问题,结论如下:
a. 装配预紧力不足会导致接触面开合,弹性恢复发生撞击是产生异响的原因;
b. 过载冲击交变载荷作用下,如结构局部发生屈服会导致预紧力衰减,拧紧工艺设定需考虑轴力衰减的影响;
c. 本方案有效弥补了相关设计标准的应用局限性,可推广至类似的球头销装配力矩设定或预紧力衰减问题的结构优化。

