新型电缆支架强度有限元建模与可靠度分析

黄振喜，张超，涂磊，邹相国

（1.国网湖北省电力有限公司，湖北 武汉 430077；2.湖北省电力勘测设计院有限公司，湖北 武汉 430040）

1 前言

随着国家经济的持续发展，城市建设进程不断加快，城市输电需求与土地资源的矛盾也日趋明显。不同于以往广泛采用的架空输电线路，通过电力隧道敷设地下电缆线路的思路，提高城市供电可靠性，已经成为城市供电难题的优化解法，也是解决今后城市输电瓶颈的着力点。

电缆支架用于支承、固定隧道内的高压电缆，是电力隧道的关键构成部分。目前，城市供电线路中的圆形断面隧道内都采用弧形电缆支架系统。楚济祥系统梳理了地铁隧道中的电缆工程支架技术。李春对电缆支架在设计中容易出现的问题进行分析并给出合理建议。

但上述工作均未涉及或仅少量涉及支架的精确数值建模计算，以及后续的结构优化工作。本文以武汉西郊220kV 架空输电线路迁改落地工程为背景，研究电缆支架的材质和结构选型确定后的静力学建模计算，并在此基础上给出改善建议，也为相关工程的建设提供参考及一定的理论指导。

2 电缆支架材质及结构选型

2.1 工程概况及基本要求

电缆支架材质和结构选型的影响因素较多，其首先受到工程的实际条件约束。武汉西郊220kV 架空输电线路迁改落地工程全线采用隧道敷设，线路折单后的总长度超过20km，全线分别采用了2×ϕ3.2 顶管法或者盾构法圆形隧道、单圆盾构法隧道分舱敷设等结构形式。线路电缆并排形布置、垂直蛇形敷设，支架纵向层间距为0.5 ～1m 不等。其次，电缆支架需要满足敷设施工、运行、检修、抢修等不同阶段的承载和变形要求，同时，要满足防火防潮、及耐久稳固方面的要求。图1 为典型条件下圆形隧道的支架结构示意图。

图1 圆形隧道内电缆支架结构示意图

2.2 支架材质、型式及荷载

根据现有的规程规范要求，在极限大电流超过1000A 的工程下，支架需选用非导磁金属材质。同时，考虑到典型的蛇形敷设，在垂直方向上电缆自重荷载相当大，因此选用静力学性能较好的不锈钢材质。

如图2 所示，电缆支架上的恒载包括三个部分，即支架的自重、电缆的自重和电缆夹具自重三个部分，在220kV 电缆工程中，电缆及其夹具的重量占据了支架恒载中的绝大部分。根据线缆厂家提供的出厂参数，以及电气设计提资等综合来看，220kV 高压线缆单根重量约40kg/m，电缆接头长度约2m，重量约180 ～200kg/m，电缆支架上每回电缆含3 根电缆(三相呈品字形布置或一字型布置)。对于长支架，则支架上摆放2 回电缆，或1 回电缆与1 个接头，取恒荷载分项系数1.3，活荷载分项系数1.5，最终得到支架荷载及尺寸设计值，如表1 所示。

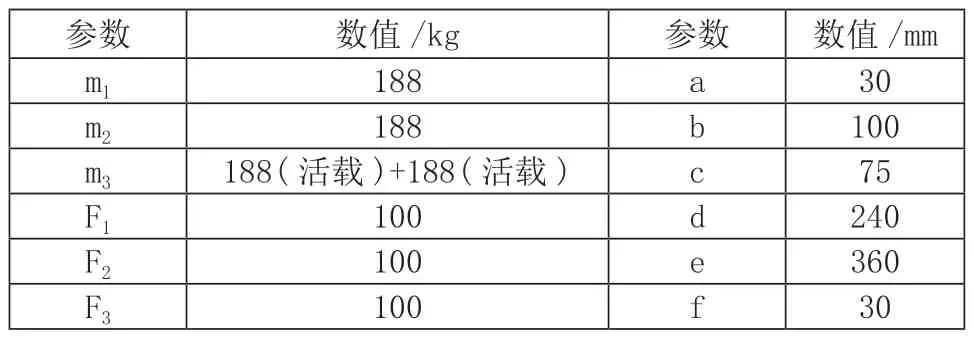
表1 支架荷载及尺寸设计值

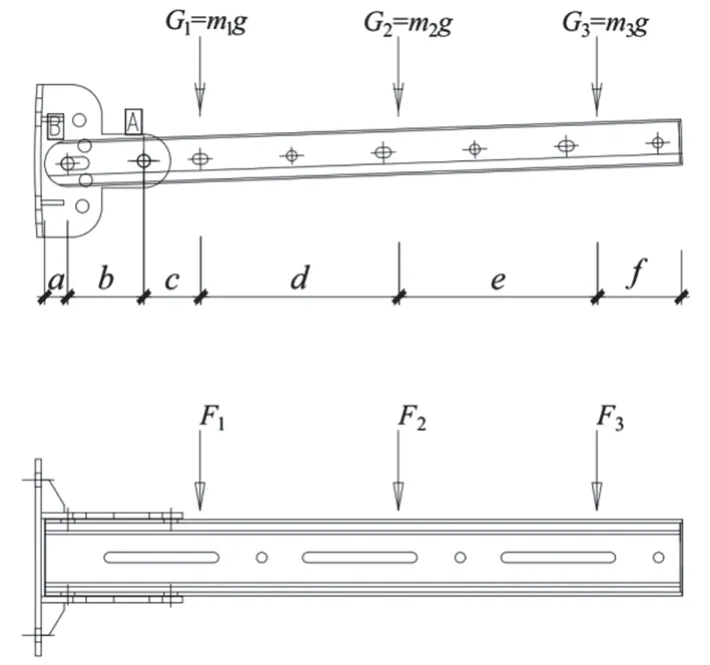
图2 支架电缆单元及荷载示意图

3 静力计算

3.1 有限元模型

有限元建模时，约束条件如图3（a）所示，螺栓紧固面1 为支座与隧道关闭的四个螺栓紧固面，采用固支约束；螺栓紧固面2 为支座与支座横担的两个接触面，采用相对滑移较小的绑定关系；外载荷为三对集中力，参照表1 施加。在划分网格时，采用C3D8 单元，由于支架横担含有内部加筋结构，同时与支架固定部分有螺栓连接等局部开孔结构，考虑采用实体单元建模，网格划分采用自由四面体，单元尺寸4 ～8mm，在应力集中区适当加密网格，如图3（b）所示，确保收敛情况下整体模型单元数量约为823466 个。

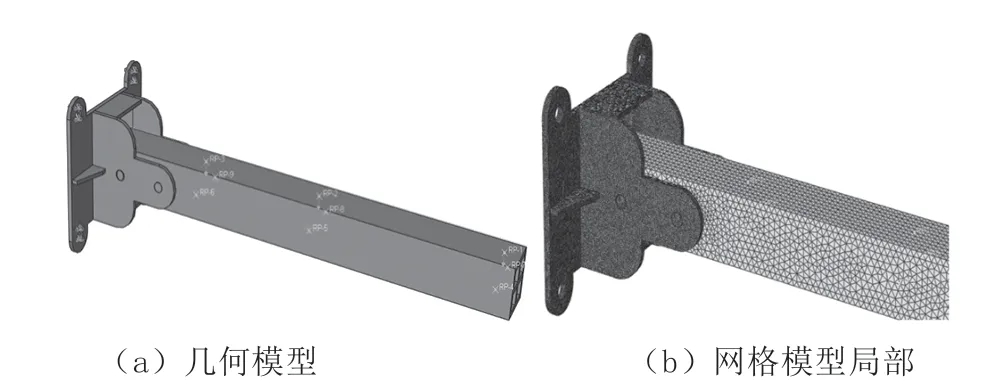
图3 有限元模型

支座为不锈钢材质，其材料参数杨氏模量E=210GPa，泊松比σ=0.3，密度ρ=7850kg/m3，计算考虑自重，g=9.8m/s2。

3.2 计算结果

对缆支架有限元模型计算求解，得到位移及应力云图，如图4（a）～（c）所示，可直观体现支架应力及位移分布情况。

图4 有限元计算结果

可以看出，由于建模过程较为精细地反映了螺栓连接等细节，得到的位移结果也相对一些采用悬臂经验公式的理论计算结果也更为可靠，静变形最大值为20mm，如图4（a）所示，形变量约为1%，受力明确，整体处于安全状态。

此外，支架横担受力后，通过与之锁附的螺栓将剪力传递至支架。且竖向荷载作用下，左侧靠近支架端部的螺栓孔的下半部与螺杆接触，右侧远离支架端部的螺栓孔上半部与螺杆接触，应力在此处集中（图4（b）），支架端部与管壁固接的4 个螺孔位置也是应力集中区（图4（c））。

等效应力的整体分布上，最大值为275MPa，出现在支架横担的应力集中区。尽管支架端部是与隧道管壁接触的大平面结构，这在理论上还有结构拓扑优化的空间，但在工程中应力峰值远小于Q355 钢材的屈服强度值，已经在使用容许范围内。

4 性能退化计算

4.1 时变可靠度指标

在服役时间、外部载荷和自身材料等因素影响下，工程结构或构件结构会随着时间发展，其强度、可靠性等会逐渐降低。为了保证结构在服役期间的安全性，对结构进行时变可靠度分析十分重要。

电缆支架随着服役时间增加其材料性能会逐渐弱化，将其抵抗退化能力加入考虑得到材料的时变可靠度。因其内部因素和外部环境影响使结构的可靠度随时间下降。其极限方程可表示为：

其中，Z(t)、R(t)、S(t)分别表示结构的极限状态函数、抗力-时间函数、荷载-时间函数。

相应的失效概率可表示为：

其中，P(t)表示结构在服役时间时的失效概率。

时变可靠度可表示为：

4.2 Monte-Carlo 随机有限元法

为了计算出结构的可靠度，本文将有限元方法和Monte-Carlo 方法相结合，计算效率精度高、方法简单是此方法的显著优点。使用应力-强度干涉理论对支架进行可靠度计算时，将支架在不同时间段受到的应力作为随机变量，假设随机变量为x，其概率密度函数和功能函数分别为和。

对随机变量依据其满足的分布函数进行抽样，将随机产生的抽样次数设为N，计算相应的功能函数。将试验中出现的情况记为失效情况并将失效情况出现次数记为n，则失效概率p 可表示为：

4.3 计算结果

对钢材进行室外加速腐蚀实验可以得到其弹性模量指标，钢材的弹性模量随着失重率退化而具有线性规律。本文根据参考文献实验数据得到的弹性模量与退化失重率之间的拟合函数为：

根据实验结果设计支架在服役时间30 年间材料性能逐渐退化，具体弹性模量数值与失重率如表2 所示。

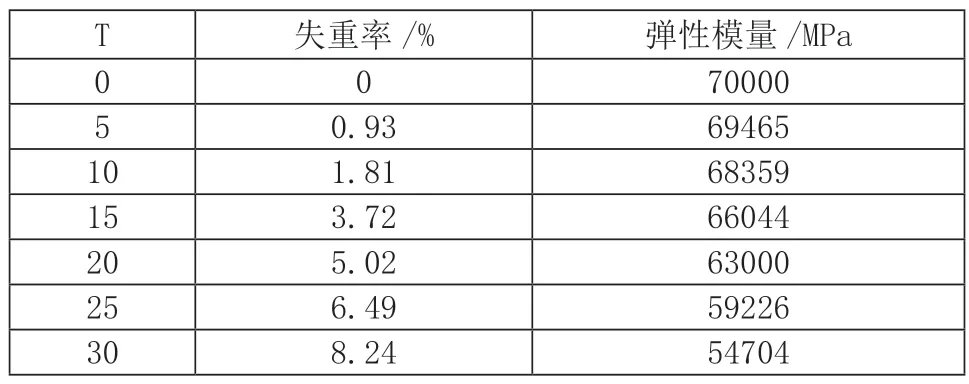
表2 钢材力学性能指标

结合式(3)、(5)，采用应力-强度干涉理论对支架横担梁进行可靠度分析模拟，结果如表3 所示。在服役时间为30 年时，横担梁的可靠度指标为2.3751，失效概率为0.88%。

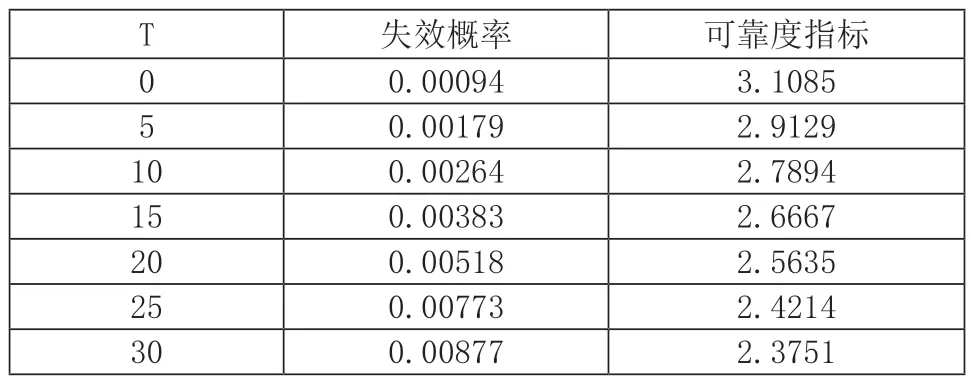
表3 性能退化下支架横担可靠度结果

由图5 可得，支架横担在服役期间，随着材料性能的退化，其可靠度指标随时间增加而减小，其失效概率随着可靠度指标减小而逐渐提高。在服役时间达到20年时，支架横担的可靠度指标明显加快降低。因此，需要在此时对支架进行安全评估和维修。在对支架进行可靠性分析时，考虑时变特性下的可靠性更符合真实情况。

图5 材料性能随时间变化时的失效概率及可靠度

5 结语

本文基于结构有限元方法，精细建立了电力隧道中一种新型支架的静力学模型。通过有限元模拟还原其在真实荷载下的应力分布情况，引入可靠度指标确定了其设计的安全性，以及应力位移的分布规律。在此基础上可得到以下结论。

（1）支架横担为主要承力部分，其受力后螺栓将剪力传递至螺栓及支架。应力分布详情明确，支架端部与管壁固接的螺孔位置、支架与横担固接的螺孔位置为应力集中区，后续可在符合工程实际的情况下进行局部加强。

（2）考虑材料性能退化更符合真实情况，并且可靠度指标呈线性变化。在支架服役期间，可以根据可靠度与材料退化规律之间的线性关系预判出其极限服役时间，设计人员可据此保证支架的安全性、可靠性、稳定性。