改进水循环优化BP 神经网络的大坝变形预测

胡振东，郭明强

（1.武汉智绘蓝图科技有限公司，湖北 武汉 434000；2.中国地质大学（武汉） 地理与信息工程学院，湖北 武汉 434000）

建筑工程在使用和运维过程中受荷载变化、环境侵蚀、人类活动等因素影响会产生不同程度的结构形变，若不能及时处理，日积月累将导致建筑物发生裂痕，造成安全隐患。因此，及时准确预测建筑物变形趋势，对于保护人民群众的生命财产安全具有重要现实意义[1]。目前的建筑物变形预测方法包括统计建模法、时频变换法和人工智能法3 大类，统计建模法认为建筑物的变形过程可利用精确的数学模型进行描述，模型确定后建筑物未来的变形趋势也随之确定，以自回归滑动平均[2]、卡尔曼滤波[3]和灰色理论[4]等方法为代表，适用于预测建筑物的短期变形趋势，长期预测精度将明显降低[5]；时频变换法认为将时域非线性、非平稳的变形序列转换至频域、时频域等变换域后会具有更简单的结构形式，更适合预测变形趋势，以小波变换[6]、短时傅里叶变换（STFT）[7]和局部均值分解（LMD）[8]等方法为代表，通常能获得较高的预测精度和较强的噪声稳健性，但小波基函数、STFT窗长和LMD分解层数的确定问题制约了该类方法的推广应用[9]；人工智能法是随着机器学习和神经网络发展而兴起的一类数据驱动方法，以支持向量机（SVM）[10]、BP 神经网络[11]和长短时记忆神经网络[12]等方法为代表，由于具备自适应自学习能力，其预测精度明显优于统计建模法和时频变换法，缺点是需要高质量的训练数据且对噪声敏感[13]。本文提出了一种改进水循环算法（IWCA）优化BP神经网络（IWCA-BP）的大坝变形预测方法，首先利用经验模态分解（EMD）将建筑物复杂变形数据分解为一系列结构简单的本征模函数（IMF）和剩余项之和的形式，然后对每个IMF 建立IWCA-BP模型进行变形趋势预测，最后将结果综合叠加获得最终的预测结果。EMD的引入提升了噪声稳健性，IWCA-BP能自动确定最优网络初值，从而获得更高的预测精度和泛化能力。

1 基于EMD的变形数据降噪分解

大坝变形过程表现出典型的非线性、非平稳和波动性特征，且易受噪声污染，若直接对其进行分析并建模预测，不仅会增加预测模型的复杂度，而且噪声和干扰等也会降低预测精度。不同于时频变换法，EMD无需设置确定的基函数，而是根据数据自身的局部特征，自适应从中抽取一系列IMF和剩余项，剩余项主要包含数据中的噪声分量，而IMF能反映原始数据中隐藏的不同维度的内在特性。

对于大坝变形监测数据x=[]x1，x2，...，xD，利用EMD对其分解的主要步骤包括：①提取x的局部极大值点，利用三阶样条插值函数对其进行插值拟合，得到x的上包络曲线xmax；②提取x的局部极小值点，利用三阶样条插值函数对其进行插值拟合，得到x的下包络曲线xmin；③计算xmax和xmin的均值曲线，记为m=(xmax+xmin)；④从原始数据中减去均值曲线，即r=x-m；⑤判断r是否为IMF，若不满足，令x=r，重复步骤①～步骤④，直至其满足IMF的两个条件，若满足，则将r记为imfi，i=1，…，L，并令x=x-r，重复步骤①～步骤④；⑥迭代终止时，原始信号被分解为一系列IMF与剩余项r之和的形式，即。

2 IWCA-BP神经网络预测模型

2.1 BP神经网络

BP神经网络是目前理论最成熟的一种前馈式神经网络模型，具有自学习、自组织、自适应能力，能逼近任意复杂非线性系统以及支持并行计算等优点，因此本文采用BP 神经网络对EMD 分解得到的IMF 进行建模预测。对于本文涉及的大坝变形预测问题，BP神经网络的输入神经元为EMD分解后得到的L个IMF分量，则输入神经元向隐含层神经元的映射过程表示为：

式中，wj（j=1，…，N）为连接输入神经元和隐含层神经元的权值；θj为阈值；N为隐含层神经元数量；f()· 为Sigmoide激活函数。

得到隐含层神经元后，将其传播至输出层神经元模型，则有：

式中，ωl（l=1，…，M）为连接隐含层神经元和输出层神经元的权值；yl为网络的实际输出值；M为输出层神经元数量。

BP 神经网络的误差反向传播就是采用梯度下降法，按照D 减小的方法对wj、ωl和θj进行更新。在误差反向传播过程中，参数初值的选取对于BP 神经网络的性能影响较大，需要一种全局优化算法对初值进行寻优，以保证模型最终收敛于全局最优解。

2.2 IWCA-BP预测算法

WCA是对自然界中水分由溪流、河流汇入大海过程进行抽象而来的一种仿生算法，相较于传统粒子群算法、蚁群算法和遗传算法具有更高的运算效率。然而，传统WCA 算法的迭代步长为固定值，在最优解附近会出现振荡现象，因此本文提出了IWCA，将迭代步长与指数函数相结合，使迭代步长具备自适应变化能力，在算法运行初期采用较大迭代步长提升收敛速度，随着迭代的进行，步长逐渐减小，在最优解附近进行精确搜索，提升收敛精度。

对于BP神经网络化参数寻优问题，IWCA首先生成大小为Npop×K的初始种群矩阵，其中Npop为种群数量，K为寻优的变量个数；然后按照溪流流向河流和海洋，河流流向海洋的汇流过程对溪流、河流和海洋的位置进行更新，具体表示为：

式中，t为当前迭代次数；C为迭代步长；σ为取值在0～1的随机数；分别为第t次迭代时溪流、河流和海洋的位置；分别为第t+1次迭代时溪流、河流和海洋的位置。

每次迭代后，重新计算溪流、河流和海洋的适应度函数值，若溪流的适应度函数值小于其汇入的河流，则交换二者位置，同样若河流的适应度函数值小于其汇入的海洋，则交换二者位置。为使迭代步长具备自适应变化能力，将其与指数函数相结合，得到指数迭代步长，即

式中，Cmax、Cmin分别为迭代步长的上下限；t为当前迭代次数；max_it为最大迭代次数。

迭代终止时，海洋的位置即为IWCA 全局最优解，对应的参数值即为BP神经网络最优权值和阈值。

3 实验与结果分析

3.1 实验数据与评估指标

为验证本文方法在实际应用中的性能，采用某混凝土大坝2013-01-01—2015-03-03 的变形监测数据开展实验，数据采样周期为1次/d，共获得803期变形监测数据。对布置在河床深槽位置处坝顶的第21号采样点的位移监测数据进行分析（图1），可以看出，变形监测数据呈现较明显的非线性、非平稳特点，且受噪声影响表现出了明显的随机波动性，给变形预测带来了挑战。

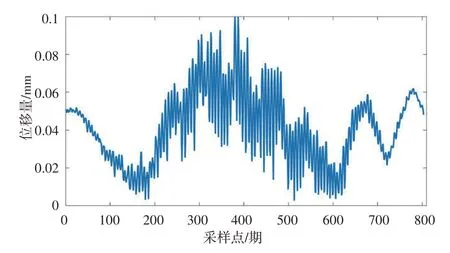
图1 大坝水平位移数据

3.2 组合预测方法的预测结果

首先，利用EMD 对变形监测数据（图1）进行分解，得到的分解结果见图2，可以看出，EMD 将复杂的变形监测数据划分为3个IMF(imf1～imf3)和1个剩余项(rL)序列，3个IMF分量的结构更加简单，且从不同维度反映了原始数据中的信息。对比图1、2 可知，EMD分解能有效降低后续预测模型的复杂度，提升预测性能。

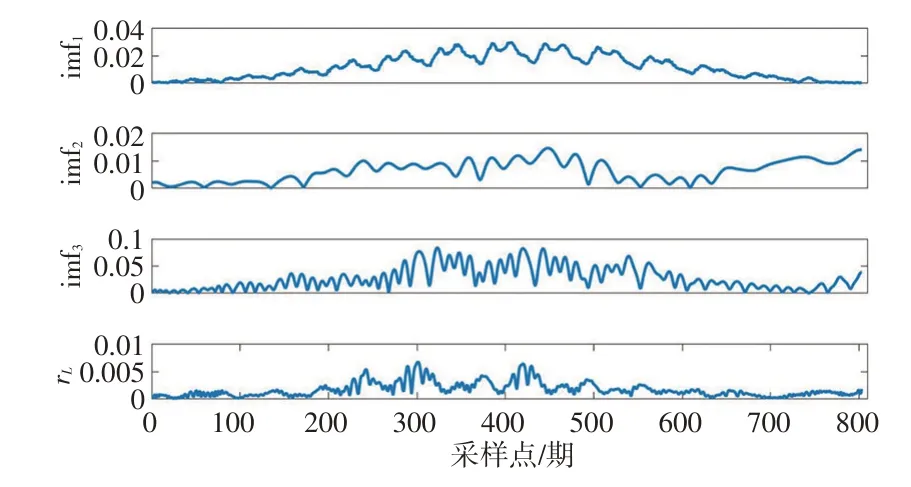
图2 EMD分解结果

然后，分别对每个IMF 建立IWCA-BP 模型进行变形趋势预测。将前500 期数据作为训练样本集合，用于模型训练和网络参数优化；剩余303 期数据作为测试样本，用于验证该方法的预测性能。综合叠加后的最终预测结果见图3，可以看出，本文方法获得的预测结果与实际变形数据较接近，能够很好地描述大坝变形趋势信息。

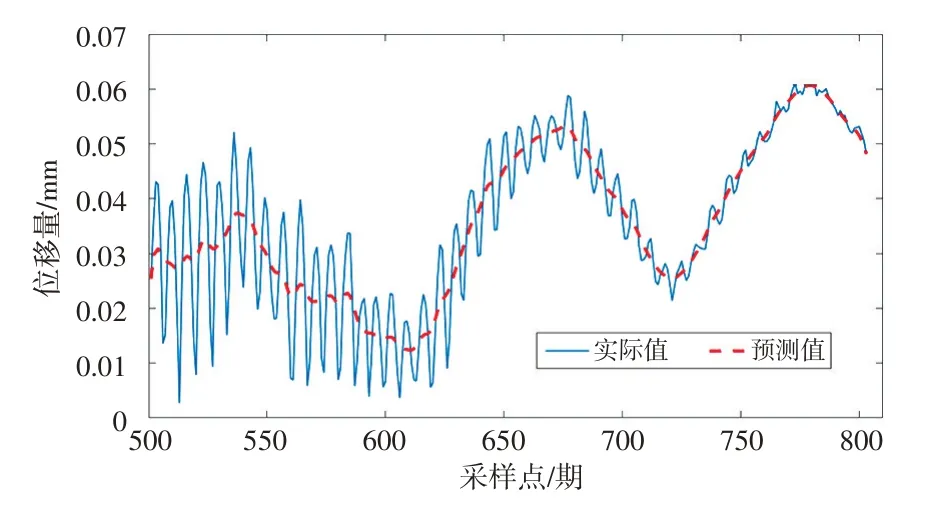
图3 本文方法的最终预测结果

3.3 与其他预测方法的对比分析

在相同条件下，分别采用卡尔曼滤波、SVM、BP神经网络、PSO-RF[14]和EMD-IWCA-BP五种方法进行预测，并统计了预测结果的RE 和MSE（表1），可以看出，卡尔曼滤波的预测性能最差，这是由于其适用于线性平稳序列建模分析，而大坝变形监测数据是典型的非线性、非平稳过程，因此预测精度低；BP神经网络的预测性能略优于卡尔曼滤波，并未表现出期望的高预测性能，其原因在于大坝变形监测数据受噪声影响较大，表现出明显的波动性，导致BP神经网络预测性能下降；SVM 的预测结果明显优于上述两种方法；PSO-RF的预测性能略优于SVM；EMD-IWCA-BP方法由于联合采用了EMD 和IWCA-BP 神经网络，具有更强的适应性能和更高的噪声稳健性，因此具有最优的预测性能，相对于PSO-RF 方法性能提升超过了32.6%。

表1 不同方法预测结果

在不同信噪比条件下，分别采用卡尔曼滤波、SVM、BP 神经网络、PSO-RF 和EMD-IWCA-BP 方法进行变形预测，得到的预测结果随信噪比的变化曲线（信噪比范围为-8～0 dB）见图4，可以看出，随着信噪比的降低，5种方法的预测性能均出现了不同程度的下降，其中BP神经网络下降最明显，信噪比为-8 dB时的预测性能比信噪比为0 dB 时的预测性能下降了88.5%，表明其噪声稳健性较差；而EMD-IWCA-BP方法在EMD 时能将噪声分量自动分解至剩余项中，通过剔除剩余项实现噪声抑制，因此表现出了较强的噪声稳健性，信噪比为-8 dB 时的预测性能比信噪比为0 dB 时的预测性能仅下降了18.4%，明显优于其他方法。

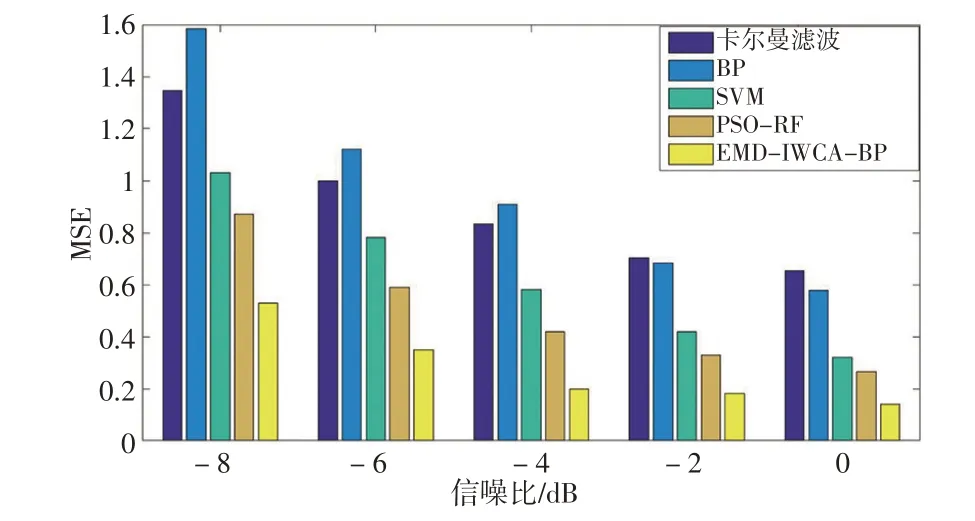
图4 不同方法预测性能随信噪比的变化

4 结 语

针对建筑物变形数据非线性、非平稳的特点，本文采用“分解—预测—重构”的方式建立了EMD-IWCA-BP模型，首先利用EMD的自适应分解能力将复杂变形数据分解为一系列结构简单的IMF 分量，同时提升噪声稳健性；然后构建IWCA-BP 神经网络对每个IMF建模预测，提升预测性能。基于实际大坝变形数据的实验结果表明，相较于传统卡尔曼滤波、BP神经网络、SVM和PSO-RF方法，本文方法的预测性能提升超过了32.6%，且表现出更强的噪声稳健性，更适合于实际应用场景。