关于恒等算符的一点思考

杨 易 邬劭轶 郭天浩 杨晓旭 苏 婕

(电子科技大学物理学院 四川 成都 611731)

1 恒等算符简介

恒等算符是量子力学的基本概念,通常定义为作用于任意状态Ψ都使其保持不变的算符,即

IΨ≡Ψ

(1)

可见恒等算符I其实是整个算符中最基本、最简单的成员,它作用于任意状态的结果都相当于没有作用.这点首先与算符作用于状态后通常会使其发生改变(即FΨ=φ)不同,属于最简单的情形.其次,也与厄密算符的本征方程[1-2]

FΨ=λΨ

(2)

有所不同,因为本征方程虽然也体现了变化之中的不变这一辩证关系,但仍然需要乘以一个常数即对应的本征值λ.而恒等算符相当于这一常数恒为1,体现了大道至简的法则.

但是恒等算符的神奇之处却在于考虑具体表象F时,任意波函数Ψ可以按该表象的共同本征函数即基矢{|k〉}展开为[3]

(3)

由于|Ψ〉为任意状态,可以得到以投影算符完全求和表示的恒等算符

(4)

其中每个分量为相应基矢的投影算符

pk=|k〉 〈k|

它使被作用的状态投影到对应基上

pk|Ψ〉 =|k〉 〈k|Ψ〉 =ak|k〉

(5)

由此可见,得益于狄拉克符号,恒等算符具有以投影算符完全求和的形式.

2 恒等算符在量子力学计算中的妙用

在量子力学计算中,可以在恰当的位置(通常是波函数与算符之间或者两个算符之间)插入恒等算符,使恒等算符中的左矢和右矢分别与旁边的状态配成内积形式,或与旁边的力学量配成矩阵元的形式,从而使计算得以化简并进行下去.例如计算两个任意态Ψ和φ关于两个算符A和B乘积的矩阵元可表为在A和B之间、Ψ与A之间以及B与φ之间分别插入单位算符的形式

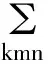
〈m|A|k〉 〈k|B|n〉 〈n|φ〉 =

(6)

其中am和bn分别是状态Ψ和φ在F表象中矢量形式a和b的m和n分量.这样就可以将看似复杂的积分化为两个矩阵元与两个系数的乘积对3个脚标的求和,从而使计算得以进行下去.

在量子力学中的矩阵力学部分,涉及的状态和力学量算符的表象变换以及基本量子力学问题中的本征值问题、平均值问题和含时薛定谔方程都可以利用恒等算符非常简捷地得到相应的表达式.其中关键的步骤就是在恰当的位置插入恒等算符,使原本乘在一起的计算分开成同一个表象下不同基矢与状态的内积(由此得到相应的分量系数)或力学量算符矩阵元.因此,上述对于恒等算符的讨论可以帮助学生理解这一概念,并在计算中灵活地加以应用.

3 恒等算符的方法论思考

恒等算符在方法论上体现了思维方法的一个亮点,即辩证法中整体与局部的辩证关系.式(4)从左到右反映的是化整为零的方法和思路,历史上著名的曹冲称象即是这样的例子.广义来看,可以对应于无法测量的整体(源头)以投影的方式降维分散于可以认知的三维空间的有限事物.

式(4)从右到左反映的是积零成整的方法.例如电动力学中计算无限大接地导电平板上方一个点电荷Q在空间产生的电势分布时,如果基于导电平板上的感应电荷来计算空间电势分布显然会很复杂,但若采用电像法就很简单,即用与点电荷Q对称位置处的点电荷ΔQ来等价替代导电平板上所有感应电荷,这样计算就会非常简单.进一步说,在常规层面(维度)解决问题通常都很复杂,甚至不可能实现,但跳出常规层面(即投影)而直接进入其源头(投影源)的话,问题也许就会变得很简单,甚至会发现压根就没有问题,只不过是看错的幻觉而已.

因此,自然辩证法中整体和局部的辩证关系可以用恒等算符的妙用充分地体现出来,为工作和学习带来一定的便利.

4 恒等算符的哲学思考

在上述分析的基础上可以对恒等算符进行哲学层面的探讨.下面从全息论和本体论的角度加以分析.

4.1 恒等算符的全息论探讨

式(4)很直观地反映了恒等算符具有全息的特征,或者说一即是一切,一切即是一,也可以说是局部与整体无二.这点在经典力学角度显然是不成立的,因为按照思想理智的逻辑,整体包含局部,局部属于整体;一属于一切,一切包含一.但这看似有悖于逻辑的现象恰恰是全息的神奇之处,此时局部与整体已然无法区分,一与一切无二无别,这正是逻辑思维的奇点,或是真正创新思维的门户.与之类似的还有现代物理三大基石之一的混沌与分形中的分数维现象,也带给人们无限不可思议的遐想[4].

因此,从恒等算符的全息论层面可以进一步理解整体与局部的辩证关系,特别是不再局限于自身的有限视角,而是从局部或哪怕一个微不足道的点顿见整体,例如从一滴水见到整个大海,从一粒沙见到整个宇宙.显然,这里的见到不是指眼睛看到.

4.2 恒等算符的本体论探讨

从上述恒等算符的性质不难看出,它具有本体的性质,如无法测量性、超越时空性(恒等算符本身不需要涉及时空,因而超越逻辑,如不动,不生不灭)、无限延伸性(即全息性)等.这里权且将之比喻为不可测量、不可分析的无限本体,用以审视经典力学(常规思维)的真实性.假设在时刻t,空间环境χ(r,t)中位置r处,观察者(即主体)Ψ对被观察对象(即客体)φ实施了测量(或操作)M(t).按照经典语言逻辑,Ψ为主语,M为谓语(动词),φ为宾语,χ(r)为)状语,则上述语言的经典力学解析为

〈Ψ(t)|M(t)|φ(t) 〉χ(r,t)

(7)

现在考察基于恒等算符的表述.如前所述,在Ψ与M之间和M与φ之间分别插入F表象角标k和j的单位算符可以将上式化为

(8)

其中Mkj是力学量M在F表象中的矩阵元.需要说明是,上述表达中近似认为空间环境与观察者或被观察对象之间不存在相互作用,即环境独立于Ψ和φ以及M.

可见,上面表达式中的主体Ψ、客体φ和测量M都可以基于恒等算符表示为相应的系数或矩阵元形式.也就是说,主客体实际上并不一定是真实存在的实体,而是恒等算符I投影出来的系数组合,或者说主客体都还是测量(或操作)M所测量出来的,其中并没有测量者,也没有被测量的对象,只有测量M本身.因此,经典力学(或逻辑)所定义的主体和客体严格说应该称为伪主体和伪客体,它们只是从本不存在的虚幻参考点(基础或立场)看出来的分立独立错觉.但事实上,这种看似分立并未真正发生,Ψ和φ以及χ(r,t)本就是整体不可分割的铁板一块,如同梦境中的梦我、梦他、梦环境等等就是不可分割的同一个整体,即梦境本身.

进一步,M实际上也并非实实在在的测量,而只是由于测量者(主体)从自身立场出发的看似扭曲的操作下对该操作的一种定义,或者说恒等算符I在这种操作下看似发生了扭曲.不妨选取M自身表象(基矢设为{|α〉},本征值为λα),该操作只是如下的变形

(9)

显然,当M的本征值全为1时,自动退化为恒等算符.因此,本质上就是恒等算符自己对自己的操作(或测量),因为伪主体本身并不真实存在,唯一能作用的主体当然只有恒等算符本身.而经典力学(或传统逻辑)所谓的主体和客体其实都是I所测量出来的,并无实体可得.虽然从算符M角度看自己存在扭曲的情形,但恒等算符却从来都只看到自己,根本无所谓扭曲不扭曲这样的戏论,甚至也完全没有必要定义自己为恒等算符.

再说一下空间环境和时间变量.本来恒等算符中并无时空,但却蕴含一切时空的种子,所以作为状语的空间函数(以及时间)本质上也是恒等算符所变现出来的,并非如经典力学所认为的刚性实体框架.那么进一步考察式(7)和式(8),可以基于恒等算符描述为:I在自己显现的时空环境里,投影出伪主体Ψ,对投影出的伪客体φ,看似实施了测量M.最后需要指出的是,被观测对象φ通常局域叠加态的性质,但观测者意识的参与会导致退相干现象,即导致叠加态坍缩为某个确定状态[5].虽然意识本质上仍然体现了非局域化量子态的不确定性,但其追求确定性的运作方式(即以快照方式在无限不可分割的动态中进行分割截取并将之固化)直接产生了因果逻辑乃至语言文字等.综上所述,恒等算符可望搭建经典力学语言与量子力学语言之间的桥梁,也为意识和思维以及语言的进一步探索提供了一定的新思路.

5 结束语

本文简要介绍了恒等算符的概念及其量子力学计算中的应用,并探讨了这一概念在方法论和哲学层面的一点启示,揭示了这一概念与自然辩证法中一些重要原理具有相通之处.另外还说明,通过对恒等算符的理解有助于学生深刻把握量子力学以及现代物理中不同于经典力学的独特思想精华.