限制回旋加速器中粒子最大能量的几个因素

李志强 龚 晖

(华中师范大学第一附属中学 湖北 武汉 430223)

1 回旋加速器最大能量的限制因素

回旋加速器的出现是加速器发展史上的重要里程碑,它使得人类不仅创造了当时人工加速带电粒子的能量记录,更重要的是它所展示的回旋共振加速方式奠定了人们研发各种高能粒子加速器的基础.

最早的回旋加速器虽然已经突破了当时加速带电粒子的能量记录,但其最大能量依然受到几方面因素的限制,后来人们为了突破这些限制而在其基础上做出了许多改进.下面分别列举和分析这几方面的限制.

1.1 限制因素1:D形盒半径和磁感应强度大小

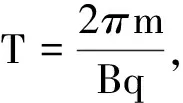
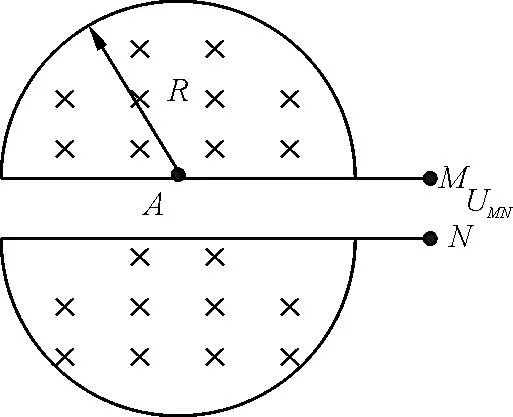
图1 回旋加速器示意图

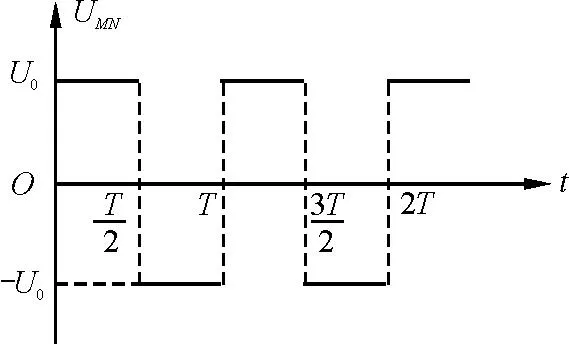
图2 回旋加速器极板电压变化图

此时有

粒子动能

解得粒子最大动能

可见,对于特定的粒子,D形盒半径越大,磁感应强度大小B越大,粒子达到的最大动能越大.

1.2 限制因素2:粒子经过极板间隙的时间

其他条件与第一种情形相同,但粒子经过加速极板的间隙的时间不能忽略.不妨假设间隙距离为d.

设粒子在t=0时刻,从A点飘入加速极板之间(初速度不计),则粒子每加速一次,在磁场中运动半个圆周,由于要考虑通过间隙所花时间,粒子的运动便逐渐滞后于电场的方向变化,当积累到一定程度时,电场方向与粒子运动方向不再匹配,就不再能加速,此时便达到最大速度.下面做一些简单计算.

粒子第n次经过极板间隙所花时间

n次加速导致粒子总滞后的时间

Δt=Δt1+Δt2+Δt3+…+Δtn

可知

其中

联立上面式子计算可得

因此,最大动能

可见,由于粒子经过极板间隙时间的影响,极板间隙越大,所能获得的最大动能越小,但加速电压越大,所获得的最大动能越大.

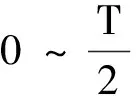
1.3 限制因素3:相对论效应

为了使分析过程更简洁,在这一部分,我们不考虑前文所述的两种限制.其余条件都不变,但此处要考虑粒子速度增大后,质量也相应变大,从而导致粒子在磁场中运动周期变大,因此每在磁场中旋转半周,粒子的运动滞后电场的变化,这称为“相位滑动”[1]80,当滞后的总时间达到某个值时,粒子速度方向与电场方向不再匹配,不再能被加速,此时就达到了最大速度.下面做一些具体计算.

记粒子的静质量为m0,电场变化周期

假设粒子在t=0时刻初速度从A点进入加速极板之间.根据狭义相对论,动能为Ek时,粒子质量满足

mc2=m0c2+Ek

设粒子经过n次加速后质量为mn,在磁场中旋转周期为Tn,则

mnc2=m0c2+nU0q

由于

可得

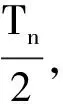
代入计算得

前n次滞后的总时间

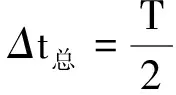
解得

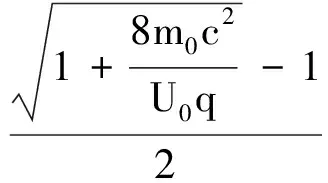
E′m=NU0q

可见,增大加速电压U0有利于增大粒子的最大动能.

顺便一提,第三种限制的习题还很少见,上述分析过程即可命制成适合高中生的习题,定会让解题者对于此种相对论效应带来的限制理解更加深入.

2 对3种限制因素的比较

经过分析上述3种限制因素,读者可能会问,当3种因素同时考虑时,粒子的最大能量到底能达到多大.接下来我们借助实际的回旋加速器参数,分别计算上述3种因素单独作用的情况下粒子的最大动能,以期对3种因素的主次关系有更明晰的了解.

以质子为例:

质子质量m= 1.67×10-27kg,带电荷量e=1.6×10-19C,设磁感应强度B=1 T,加速电压U0=100 kV,这基本符合回旋加速器的实际参数[1]83.

对于限制因素1,设D型盒半径R=1 m,可以计算得质子被加速的最大动能约为48 MeV.

对于限制因素2,设加速电极之间的间隙d=1 cm,允许的质子最大动能约为1015MeV.

对于限制因素3,允许的质子最大动能约为14 MeV.

因此,从上述数据的比较可以看出,限制因素3对最大动能的限制起主要作用.而且,为了使粒子在径向(垂直于磁场,垂直于粒子速度方向)和轴向(垂直于D形盒中面)的运动能够稳定,必须保证从D形盒中央往边缘磁感应强度逐渐减小[1]77-79.所以实际的回旋加速器中,粒子运动半径越大,磁感应强度越小,粒子运动的周期越大,这相当于加剧了粒子的“相位滑动”,使得限制因素3所允许的粒子最大动能更小一些.

为了克服限制因素3,获得更大的粒子能量,物理学家进一步发明了等时性回旋加速器,即通过设计产生磁场的极板的形状,使得粒子运动轨道上的平均磁感应强度随半径增大而增大,这会使粒子回旋周期减小,如果正好与因速度增大、质量增大而使周期变大的数值互相抵消,从而补偿限制因素3中所提到的“相位滑动”,使粒子的旋转周期在加速过程中始终保持恒定,这样的等时性回旋加速器能够消除相对论效应的影响,从而提高粒子的最大能量,等时性回旋加速器的最大粒子能量可以达到几百MeV.而另一种方案是稳相加速器,即随着粒子绕行半径增大,逐渐减小加速电场的频率,以达到相位稳定,稳相加速器能达到的最大粒子能量约为1 GeV,再往后,由于经济和技术的限制,占据主流的是弱聚焦同步稳相加速器.