对一道范艾伦辐射带试题的深入分析及可视化仿真研究*

潘 刚 李阳辉 陈文娟 王姝舒

(合肥工业大学宣城校区 安徽 宣城 242000)

1 引例问题

北京市丰台区2021届高三上学期物理期末试题有这样一道题目:如图1所示,来自外层空间的大量带电粒子进入地磁场影响范围后,粒子将绕地磁感线做螺旋运动,形成范艾伦辐射带.螺旋运动中回转一周的时间称为周期,回转一周前进的距离称为螺距.忽略带电粒子之间以及带电粒子与空气分子之间的相互作用,带电粒子向地磁场两极运动的过程中( )

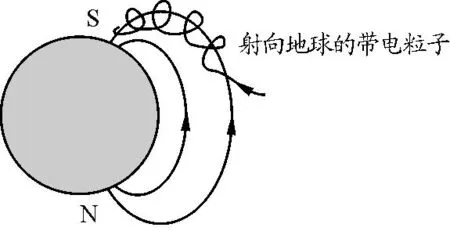
图1 范艾伦辐射带示意图

A.粒子运动的速率逐渐变大

B.粒子运动的周期不变

C.粒子螺旋运动的半径不变

D.粒子螺旋运动的螺距逐渐变小

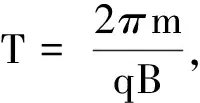
其实本题有一定的难度,参考解答的思路是将带电粒子在匀强磁场中的运动规律——沿磁感线方向的运动速度不变运用到该题中,从洛伦兹力不做功得出粒子的总速度大小不变,再从粒子沿着磁感线方向的运动速度不变得出粒子垂直于磁感线方向的运动速度也不变,最后根据所学的半径和周期的公式得出答案.这样的解答思路主要是考虑到高中生的物理知识储备,简单易懂,得出的结论也没有问题,但分析过程与实际情况还是存在偏差的.因为与匀强磁场不同,粒子在非匀强磁场中沿着磁感线方向的运动速度实际上是在不断变化的.所以学生在解答完本题后难免会有以下疑问:粒子运动到地磁场两极后又将如何运动?运动题目中所涉及的范艾伦辐射带到底是怎样形成的?范艾伦辐射带中不同粒子在不同条件下的运动会有何差异?基于此,本文先对带电粒子在地磁场中的运动进行理论分析,再运用有限元仿真软件对范艾伦辐射带的形成进行可视化仿真研究,彻底解决学生的这些困惑.

2 磁镜结构与范艾伦辐射带简介

2.1 磁镜结构

磁镜是由两个通电线圈同轴排列且间隔一段距离产生的一种磁场分布,如图2所示.

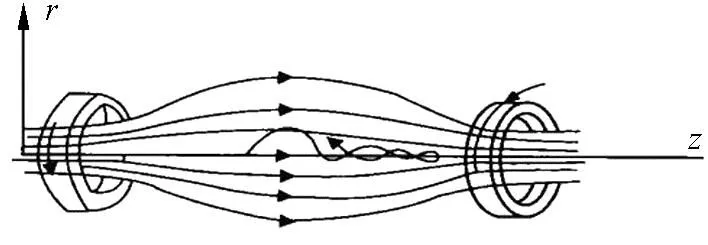
图2 磁镜结构

磁镜结构的磁场分布特点是两端磁场强度大,越靠近中心磁场强度越弱[1-2].带电粒子从磁场较弱的区域进入磁场较强的区域时,会受到“阻力”,从而使粒子沿着磁感线方向的运动减速(这一点会在下面的理论分析中给出证明).由于洛伦兹力不做功,总速度大小不变,带电粒子的旋转速度会增加.当粒子沿着磁感线方向的速度减为零以后,粒子就会反方向运动,当运行至另一端时又会反向运动,周而复始.粒子往返于磁场两端,如同光线在两镜面间发生的反射,这也是磁镜名称的由来[3].

2.2 范艾伦辐射带形成的理论分析

地磁场的场强分布与磁镜类似,在两端磁极处较强,中间偏弱,因此地球具有天然的磁镜结构.宇宙中的大量带电粒子进入地磁场后,会绕地磁感应线做螺旋运动,由于地球两极处磁场最强,做螺旋运动的粒子将被反向折回,并在地球两极间来回振荡,最终形成范艾伦辐射带[4].

带电粒子在地磁场内主要做3种典型的运动:旋转、反射和漂移.对带电粒子在地磁场中的运动可作以下理论分析.首先,在地磁场中截取一段磁感线作为分析对象:如图3所示,空间磁感线B矢量(下文以B代替)与带电粒子速度v矢量(下文以v代替)方向大小均不一样,在xy平面以及z轴中,对以上两矢量进行分解.v可分解为平行于xy平面的vxy(即带电粒子的旋转速度)和垂直于平面的vz(即带电粒子沿着磁感线方向前进的速度).同理,B可分解为平行于xy平面的Bxy和垂直于平面的Bz.带电粒子受到的总洛沦兹力[5]为

图3 空间的B矢量和v矢量

F=(vxy×Bz+vz×Bxy+vxy×Bxy)q

在带电粒子沿z轴正向运动时,总洛伦兹力中的vxy×Bz项的方向指向圆心,提供粒子进行旋转的向心力;vz×Bxy项提供的切向加速度会加快旋转的切向速度vxy,方向为旋转圆任意一点的切向方向;vxy×Bxy项的方向与粒子运动方向相反,从而使vz不断减小.与此同时,粒子的旋转半径也在不断减小,这是由于越接近磁极处,横向磁场越小,则总洛伦兹力的方向近似指向旋转中心,因此粒子的角动量L=mvxyr基本不变(r是任意时刻的旋转半径)[6].所以随着vxy不断增加,r会不断减小直至反弹.至于带电粒子的旋转周期,由于只与质荷比及磁感强度有关,随着磁感强度变大周期变小.螺距为沿着磁感线前进的速度与周期的乘积,必然也会变小.

当vz减小到零并反向增加时,粒子发生反射.反射后由于此时粒子的vz方向和vxy方向均与之前情况相反,总洛伦兹力中提供的切向加速度和平行于z的反向加速度方向同样相反,这导致粒子会重复之前的运动.由于地磁场分布并不完全对称,粒子在反射过程中会发生漂移,从而在地球两极间做围绕地球转动的周期性运动[7-8].

3 范艾伦辐射带的仿真建模

3.1 地球模型及物理场的建立

首先利用CAD软件按1∶1的比例制作一个半径为Re(Re为地球真实半径)的地球模型并导入到COMSOL Multiphysics仿真软件中,再建立一个半径为5Re的较大球体作为仿真区域,如图4所示.

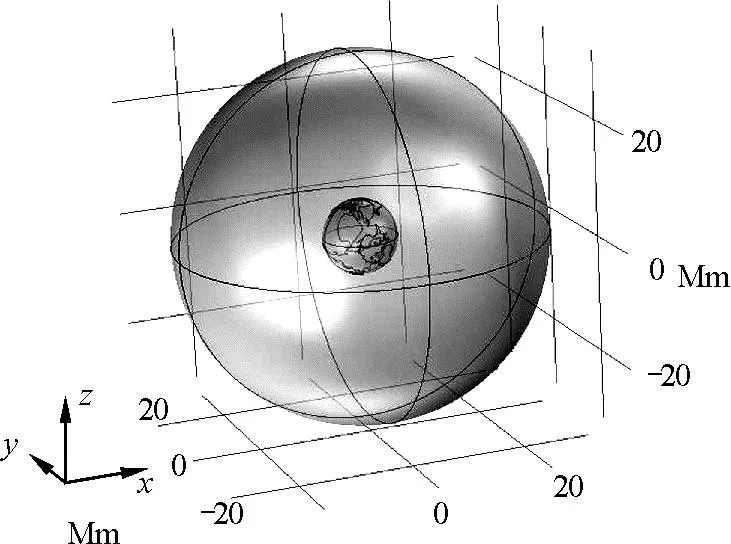
图4 仿真区域设定

物理地磁场模型采用国际地磁参考场模型 (IGRF),IGRF模型中的磁感线如图5所示.

图5 IGRF磁场线图

3.2 全局参数设置

在COMSOL中模型开发器窗口的全局定义节点下添加全局参数:地球半径数值设为6 371.2 km;初始粒子能量决定了粒子入射速度大小,可暂定为100 MeV;入射角度代表粒子入射方向和赤道面的夹角,决定入射方向,可暂定为30°.在模型开发器窗口的“带电粒子追踪 (cpt)”节点下,选择“粒子属性 1”.在粒子属性的设置窗口中选择所需的粒子,可分别设为质子、α粒子和电子.

3.3 粒子轨迹演示

在COMSOL中选择“结果”一栏下的“粒子轨迹(cpt)1”,在数据集中找到所求结果进行演示,即可得到粒子运动的动画轨迹,如图6所示.

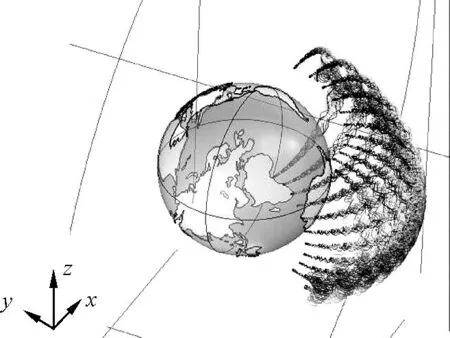
图6 粒子运动的动画轨迹

4 仿真结果展示与分析

范艾伦辐射带仿真中的粒子种类共有3种:质子、α粒子和电子.在此基础上,每种粒子初始速度由粒子的初始能量表征,粒子的初始能量分别可设为100、130、150、200、300、500 MeV.粒子入射角度范围和入射角分度值分别可设为[0,5°,20°]、[25,5°,30°]、[35,5°,40°]、[45,5°,50°]、[55,5°,60°]、[65,5°,70°]、[75,5°,85°],中括号内数值分别表示入射初始值、输入分度值以及输入终止值.

4.1 质子在地磁场中的运动

保持同一入射角度[0,5°,20°],不同能量的质子有着不同的运动状态,仿真结果如图7所示.

图7 能量变化对质子运动的影响

规律:保持入射角度不变,质子初始能量越大,单位时间内粒子偏移路程越大.

保持同一初始能量大小200 MeV不变,不同入射角度的质子也有着不同的运动状态,仿真结果如图8所示.

图8 入射角度对质子运动的影响

规律:保持初始能量不变,粒子入射角度越大,质子做反射运动的位移越小.

4.2 α粒子在地磁场中的运动

保持同一入射角度[0,5°,20°],初始能量对α粒子的影响较大,仿真结果如图9所示.

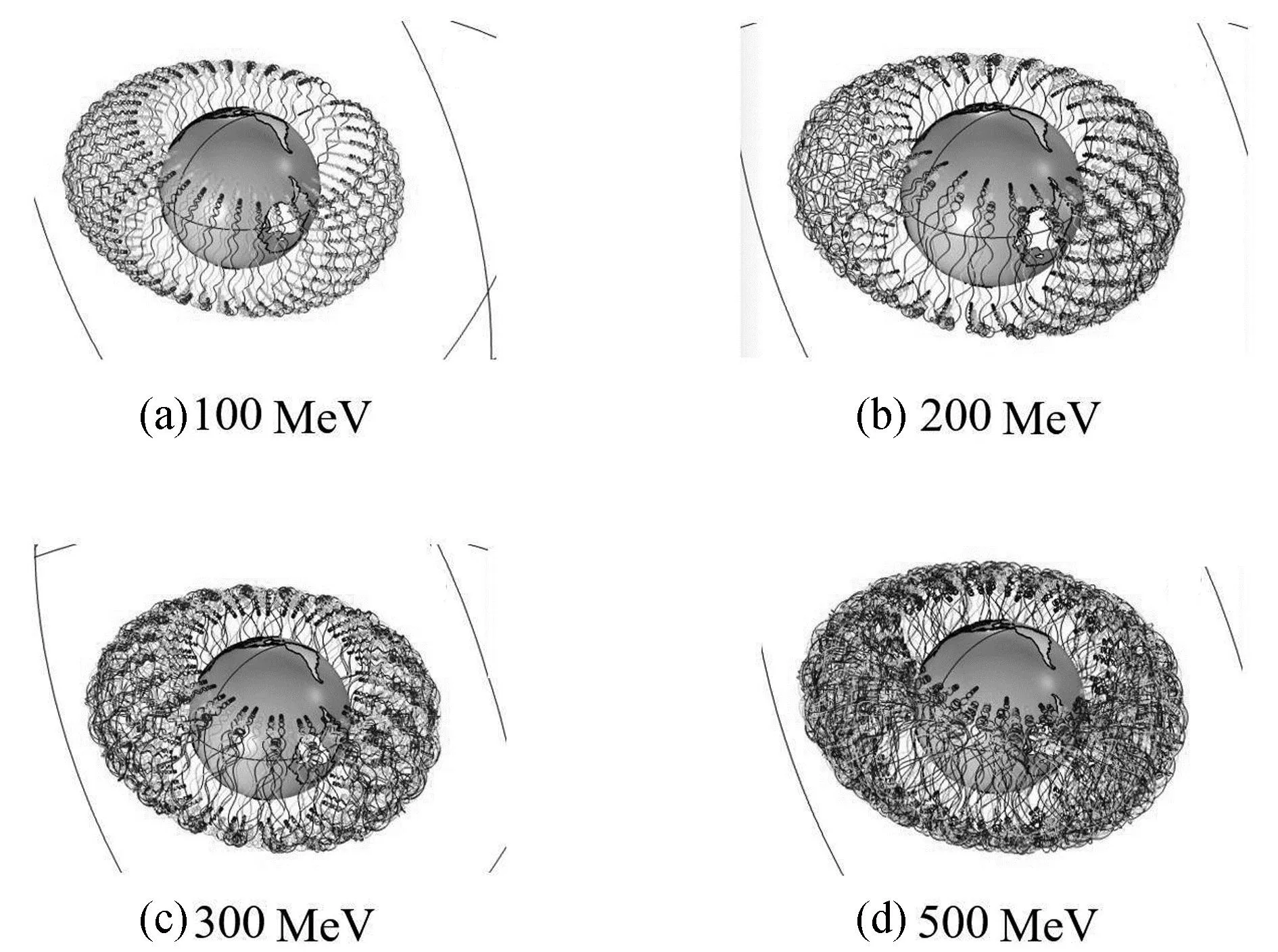
图9 能量变化对质子运动的影响

规律:保持入射角度不变,初始能量越大,单位时间内α粒子偏移路程越大.

保持同一初始能量大小200 MeV不变,不同的入射角度也会产生相应的变化,仿真结果如图10所示.

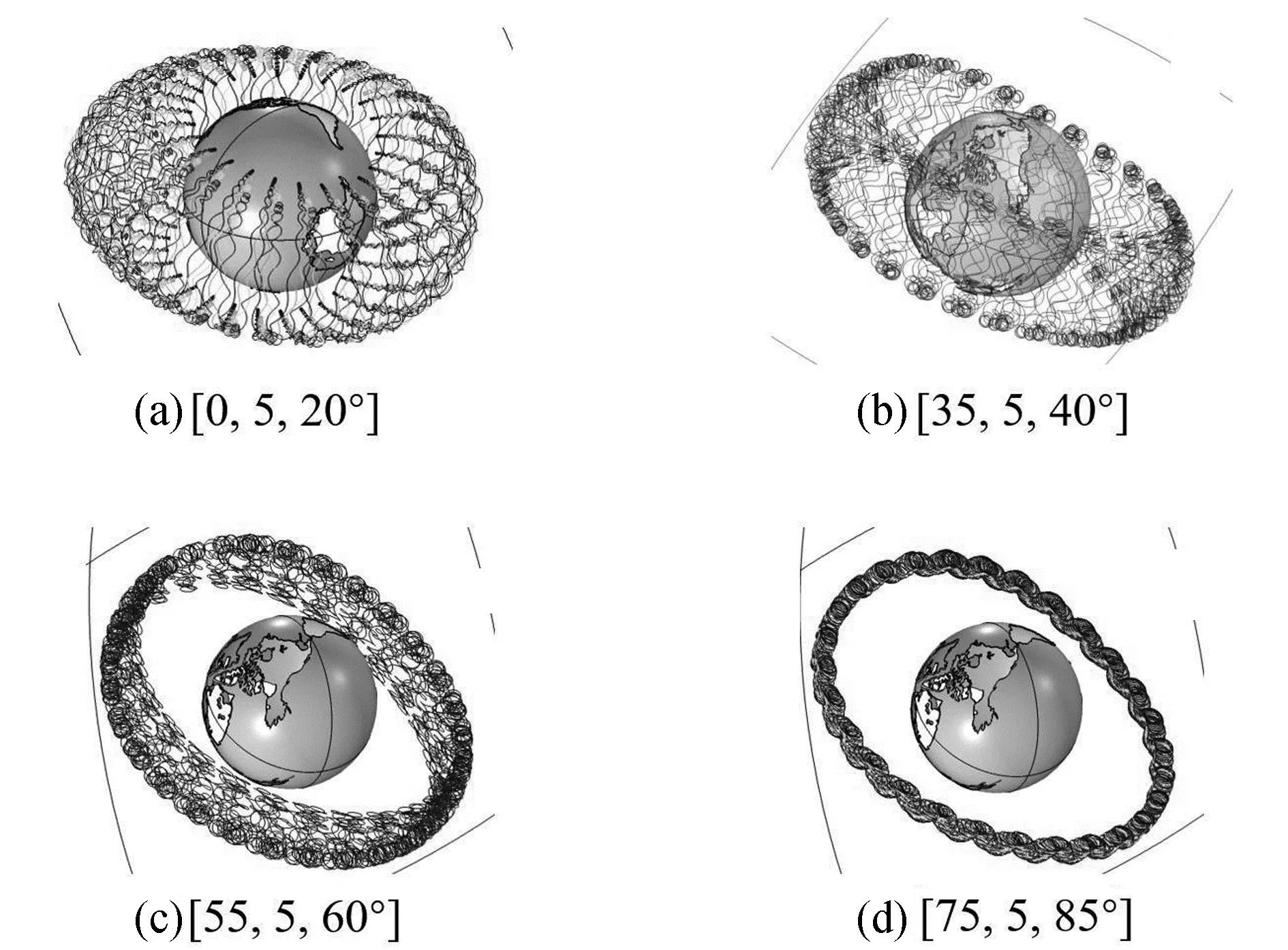
图10 入射角度对α粒子运动的影响

规律：保持能量不变,粒子入射的入射角度越大,α粒子做反射运动的位移越小.

4.3 电子在地磁场中的运动

保持同一入射角度[0,5°,20°],改变电子的能量会对电子的运动轨迹产生较大的影响,仿真结果如图11所示.

图11 能量变化对电子运动的影响

规律:保持入射角度不变,电子初始能量越大,辐射带内电子越容易逃逸.电子质量数量级远小于质子和α粒子,由于带负电荷,其漂移方向会与质子、α粒子相反.事实上,电子的能量达到较高等级时,其速度已开始接近光速,此时地磁场已很难将其捕获形成辐射带,如图11(c)和(d)所示,电子会从地磁场中逃逸.

保持同一初始能量大小200 MeV不变,改变入射角度也可对仿真结果产生影响,如图12所示.

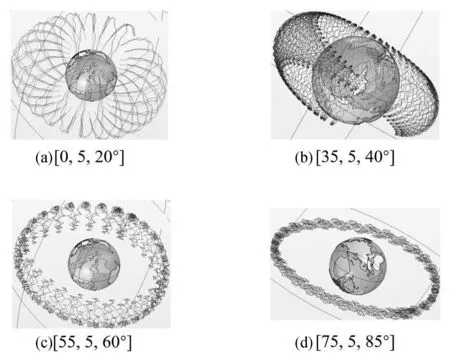
图12 入射角度对电子运动的影响

规律：保持能量不变,电子入射角度越大,做反射运动的位移越小.

5 结束语

学生对于该考题中涉及的带电粒子在地磁场中运动产生范艾伦辐射带往往存在运动图像不清晰、理解不透彻等问题,本文先运用磁镜理论对带电粒子在地磁场中的运动进行理论分析,再运用COMSOL Multiphysics多物理场仿真软件对范艾伦辐射带的形成进行可视化模拟,将不易掌握、难以想象的物理现象通过动画形式展现出来,使整个物理过程变得直观与清晰,有助于学生更全面地掌握范艾伦辐射带的相关知识.