建立合理模型 优化教学设计
——以单摆教学为例
毛登宇 帅晓红
(四川师范大学物理与电子工程学院 四川 成都 610100)
1 研究背景
近些年,我国陆续出台了相应的文件强调信息技术在教学中的应用.教育部于2012年发布的《教育信息化十年发展规划(2011-2020年)》中,明确提出要推动信息技术与高等教育深度融合,创新人才培养模式[1];2018年发布的《教育信息化2.0行动计划》中,明确提出要坚持融合创新,发挥技术优势,变革传统模式,推进新技术与教育教学的深度融合,真正实现从融合应用阶段迈入创新发展阶段[2];2019年发布的《教育部关于加强和改进中小学实验教学的意见》中,明确提出要创新实验教学方式,其中包括“促进传统实验教学与现代新兴科技有机融合,切实增强实验教学的趣味性和吸引力,提高实验教学质量和效果”[3].
另外,《普通高中物理课程标准(2017年版2020年修订)》中指出,构建物理模型是一种十分重要的科学思维方式,它旨在通过相关内容学习,使学生能在特定情境中将所研究对象抽象为一定的理想模型,知道建立模型的条件与方法,能认识物理模型在探索自然规律中的作用[4].
在此背景下,笔者将信息技术与建模教学相结合,以高中物理的“单摆”一节为例,利用计算机辅助构建物理模型,以大大提高物理建模教学的可视性,将抽象的概念、规律等进行具体形象化,以期探索一种相较于传统课堂教学而言更优更高效的中学物理建模教学形式.
2 物理模型与建模教学
模型是对真实世界的一种表征,可以对物体、事件、系统、过程、物体或事件间的关系等进行表征[5].物理学是一门自然科学,其目的在于认识与把握自然,而自然界是纷繁复杂的,人们要研究的实际问题往往有众多的因素.为了研究问题的方便,物理学上常常采用“简化”或“理想化”的方法对实际问题进行抽象化处理,保留主要因素、略去次要因素,得到一种能反映原物质本质特性的理想的物质过程或假想结构,这就是物理模型[6].
建模教学即以物理模型的建构为主要任务,教师在教学中引导学生真正认识和理解并建立起针对所研究对象的“物理模型”,以培养学生的科学思维、创新意识和创新能力等.
3 “单摆”的建模教学流程
笔者结合文献[7]所提出的“基于心智模型进阶的导引式建模教学模式”和计算机软件Tracker、GeoGebra,设计出如图1所示的“单摆”建模教学流程.
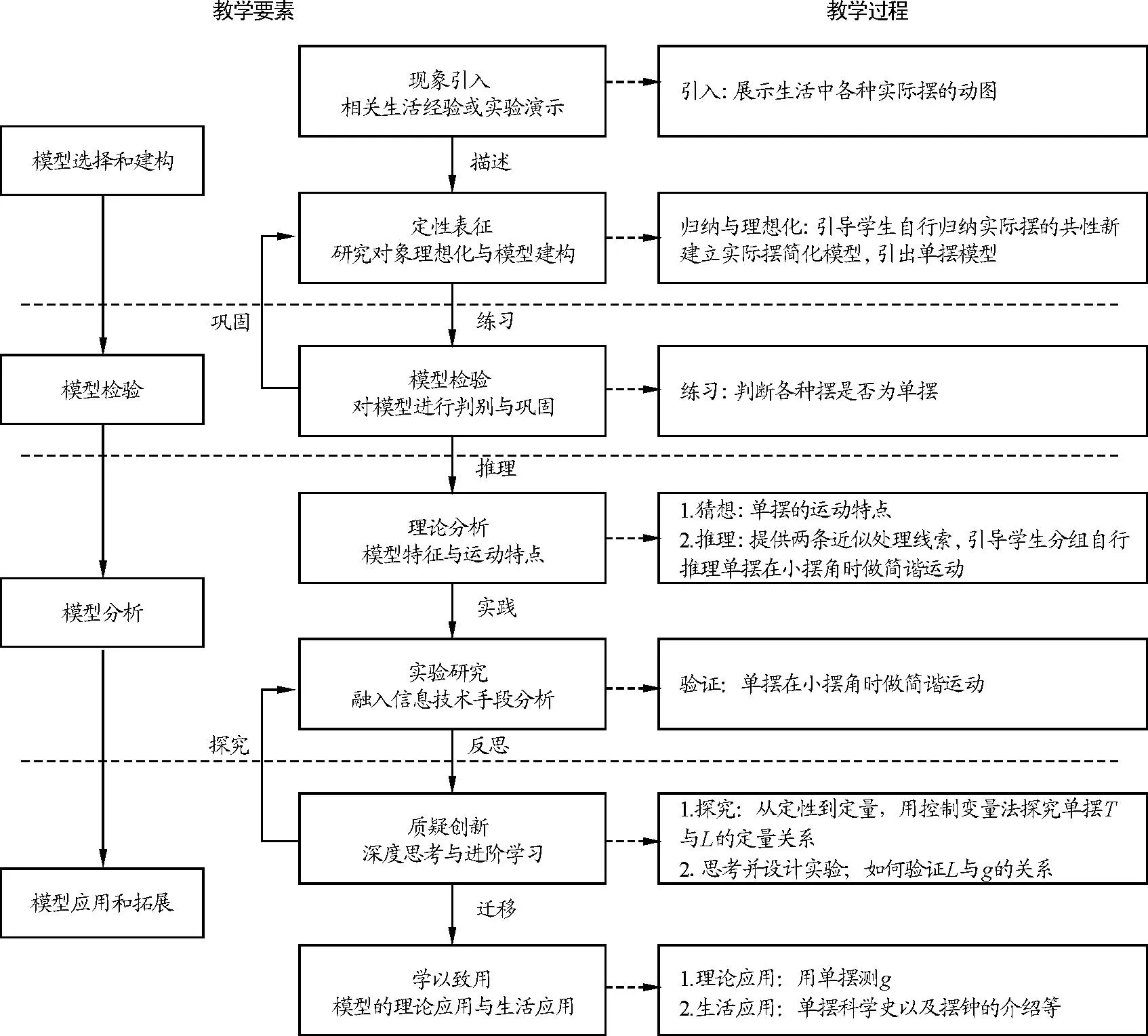
图1 “单摆”建模教学流程
4 信息技术辅助的“单摆”建模教学设计
4.1 现象引入 定性表征 模型检验
教师活动1:首先展示秋千与钟摆的动图.提问:这两者有什么共同点?请画出模型.
学生活动1:思考概括后画出图2所示模型.

图2 学生作图①
教师活动2:其次展示图3所示两张动图.提问:在刚才的基础上,悬崖秋千与拆楼重锤又有什么共同点?请画出模型.

图3 悬崖秋千与拆楼重锤
学生活动2:思考概括后画出图4所示模型.

图4 学生作图②
教师活动3:接着展示蹦极动图.提问:蹦极时人在最低点摆动,跟悬崖秋千与拆楼重锤又有什么异同点?在这里将悬崖秋千与拆楼重锤这类摆近似看作物理学上的单摆模型,所以,单摆是怎样一个模型?
学生活动3(回答):蹦极的绳子是弹力绳,而单摆的绳子是刚性绳.单摆由一根细线和一个重物组成,线一端固定,另一端系住重物;同时线长要远大于重物尺寸,并且可忽略细线伸长和质量,这样的装置就叫做单摆.
师生活动4:根据实际研究对象和研究问题,判断各种摆是否可看作单摆,以加深模型认识.
设计意图:坚持“从生活走向物理”的课程理念,通过学生的实际生活经验来引出生活中的实际摆,并以问题链的形式,引导学生由浅入深一步步经历对实际研究对象进行简化与理想化处理以构建物理模型的思维过程,知道单摆是一种重要的理想模型.
4.2 理论分析
教师活动1:引导学生讨论为什么要学习单摆这一理想模型,它到底有什么作用.因此为了弄清楚这些问题,首先需要知道单摆有什么样的运动特点.结合教材上沙摆摆动时沙子在纸上形成的图像,引导学生对单摆摆动的运动特点进行猜想.
提问:单摆摆动可能是什么运动?如何证明?
学生活动1(回答):可能是简谐运动.只要能证明单摆摆球的回复力大小与其位移大小成正比,而回复力方向与位移方向相反即可.
教师活动2:给出表1和图5所示的两条有关近似处理的线索,引导学生从力与运动关系的角度分组讨论自行证明单摆的简谐运动特点.
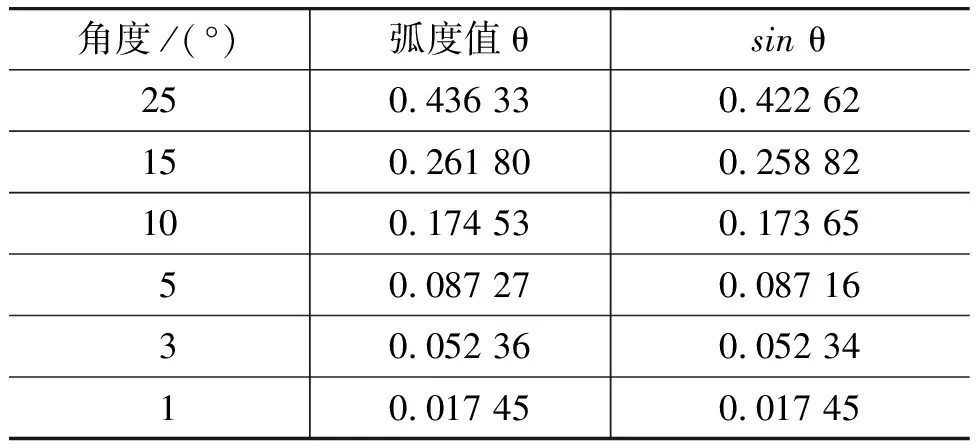
表1 角度及其对应正弦值
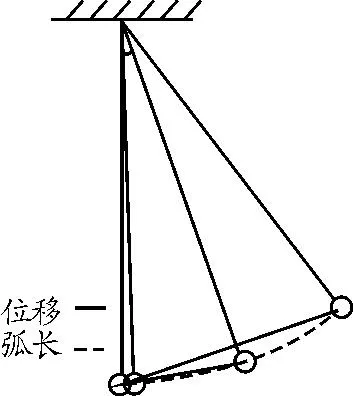
图5 单摆近似处理的图示
学生活动2:小组合作,自行证明F=-kx并将证明过程呈现在黑板上(图6).

图6 证明过程板书
得出结论:单摆在偏角很小时的振动是简谐运动.
设计意图:该环节是高中阶段单摆运动模型建立起来的核心内容.旨在引导学生理解模型建立的完整过程,学会用“简化”和“理想化”的方法对实际问题进行抽象化处理,保留主要因素、略去次要因素,得到一种能反映原物体本质特性的理想的运动过程.
4.3 实验研究
教师活动1:从运动图像的角度用实验再进行简谐运动的验证.提问:除了用F=-kx证明简谐运动外,还可以如何证明?
学生活动1(回答):证明单摆摆球的x-t图像是正弦图像.
教师活动2(演示实验):利用自制教具,通过电脑外接摄像头对单摆小偏角下的运动进行现场录像(图7),再将录像导入Tracker软件中对单摆摆球运动轨迹进行自动追踪(图8),同时自动生成其位移随时间变化的图像及数据,最后再将位移、时间数据导入GeoGebra软件进行正弦拟合(图9).结果发现拟合程度很高,则通过实验很好地验证了单摆的简谐运动特点.

图7 自制实验教具

图8 Tracker软件对单摆运动轨迹进行追踪
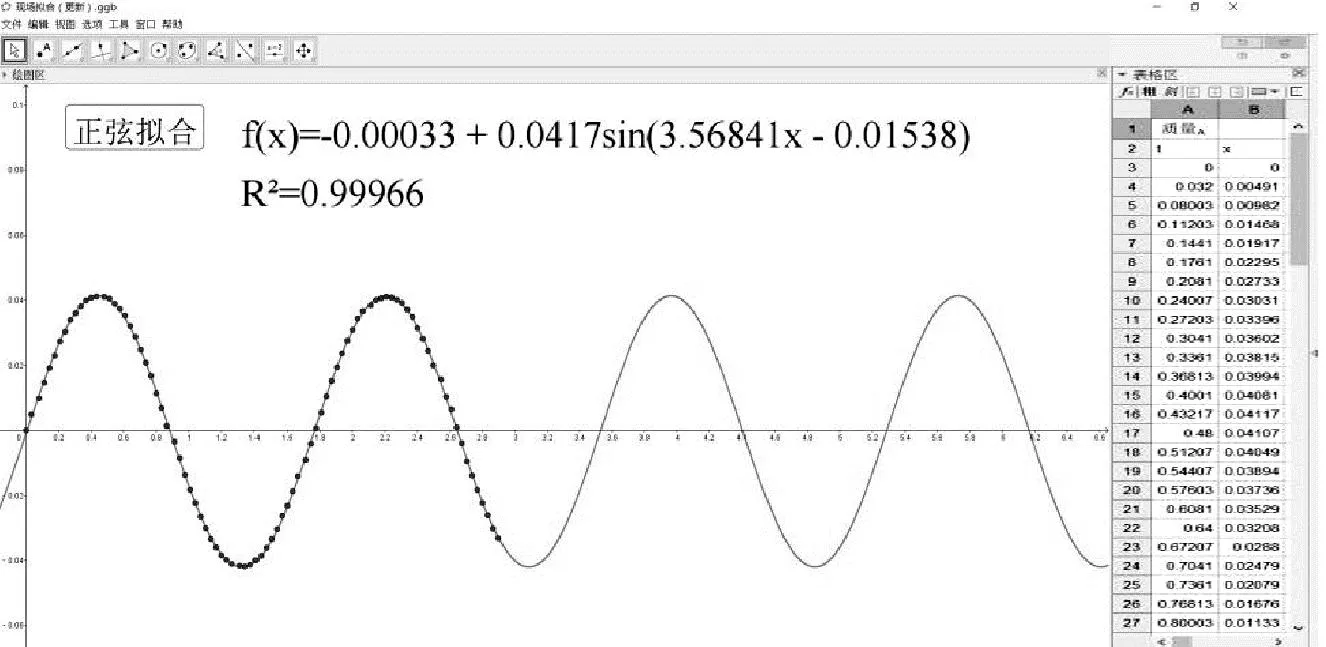
图9 GeoGebra软件对数据进行正弦拟合
学生活动2:仔细观察演示实验并思考单摆的运动规律.
设计意图:实验是物理学的基础,在单摆的简谐运动特点的理论分析之后加上实验验证,符合物理学发展的普遍规律.理论分析和实验研究分别从动力学判据角度F=-kx和正弦图像角度回归简谐运动的定义,使得教学过程完整且具有说服力,所得出的结论具有科学严谨性.另外在整个模型分析的过程中,充分利用了信息技术手段——Tracker软件实时追踪物体运动轨迹并生成运动数据,GeoGebra软件再对运动数据进行处理.因此直观地展现了动态变化过程,大大提高了建模过程的可视化程度,有利于学生更好地理解物理模型及其建立过程.
4.4 质疑创新
教师活动(提问):既然单摆运动是有周期性的往复运动,请思考其周期与什么因素有关?接着组织学生利用同样的信息化手段分组进行实验.
学生活动:通过控制变量法先定性探究单摆周期与小球质量、振幅无关,而与摆长有关.然后实验探究周期与摆长的关系,发现关系图像为曲线;接着根据化曲为直思想继续探究周期平方与摆长的关系,从而得出实验结论——单摆周期平方与其摆长成正比.
设计意图:引导学生充分利用控制变量法,小组合作从定性感知到定量进行实验探究,进一步训练学生化曲为直的思维能力,培养学生的团队合作能力、探究能力、科学严谨的求知态度.
4.5 学以致用
教师活动:呼应课堂前述问题,即“为什么要学习单摆这一理想模型?它到底有什么作用?”,讲述单摆科学史和摆钟等实际应用,并引导学生自主设计实验用单摆测量重力加速度.
学生活动:体会物理学家在科学研究中的优秀品质,学会用理论指导实践,真正将理论知识运用于生活来解决实际问题.
设计意图:坚持“从物理走向社会”的课程理念,联系实际、首尾呼应,并通过科学史来培养学生的科学精神,引导学生将思维打通,有利于学生建立起完整的物理学逻辑认知体系.
5 “单摆”建模教学设计的评价
该“单摆”的建模教学课例在第十三届“格致杯”全国物理师范生教学技能大赛中荣获一等奖,并以优秀作品被收录[8].本设计的主要优点有:
(1)“单摆”这一节,通过对比各版本高中物理教材发现,各版本教材几乎都只从简谐运动的动力学判据F=-kx来说明单摆在小偏角下的简谐运动特点,而没有从x-t关系满足正弦函数关系来说明.本文教学设计弥补了该处不足,除了从F=-kx进行理论分析外,还加入了从x-t图像角度进行实验验证的环节.这样的设计不仅培养了学生从力到运动的物理观念素养,还培养了学生从理论到实验的科学探究素养,充分落实新课标中对于培养学生物理学科核心素养的要求.
(2)本教学设计广泛加入信息技术手段的运用,如雨课堂、Tracker软件、GeoGebra软件等,这些手段相比于DIS数字化实验和频闪照相技术等具有免费、易学、简便、易操作等优点.融入信息技术手段,一方面切实提高了课堂教学的可视化程度,有利于更好地培养学生物理模型、质疑创新等的科学思维,另一方面也积极响应了国家目前大力倡导的教育信息化发展.
总之,本文建模教学以“单摆”为例,呈现了信息技术辅助建立理想模型“单摆”的教学设计,以期为广大一线中学教师和研究生提供进一步探索和研究的思路.

